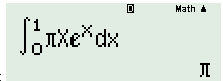50 bài tập trắc nghiệm tích phân mức độ nhận biếtLàm bàiQuảng cáo
Câu hỏi 1 : Cho \(\int\limits_0^1 {f\left( x \right)dx} = - 2\) và \(\int\limits_0^1 {g\left( x \right)dx} = - 5\), khi đó \(\int\limits_0^1 {\left[ {f\left( x \right) + 3g\left( x \right)} \right]dx} \) bằng:
Đáp án: C Phương pháp giải: Sử dụng các tính chất của tích phân: \(\int\limits_a^b {\left[ {mf\left( x \right) + ng\left( x \right)} \right]dx} = m\int\limits_a^b {f\left( x \right)dx} + n\int\limits_a^b {g\left( x \right)dx} \). Lời giải chi tiết: \(\int\limits_0^1 {\left[ {f\left( x \right) + 3g\left( x \right)} \right]dx} = \int\limits_0^1 {f\left( x \right)dx} + 3\int\limits_0^1 {g\left( x \right)dx} \)\( = - 2 + 3.\left( { - 5} \right) = - 17\). Chọn C. Câu hỏi 2 : Giá trị của \(\int\limits_0^\pi {\left( {2\cos x - \sin 2x} \right)dx} \) là:
Đáp án: B Phương pháp giải: Sử dụng các công thức nguyên hàm hàm số lượng giác: \(\int {\sin kxdx} = - \dfrac{1}{k}\cos kx + C\), \(\int {\cos kxdx} = \dfrac{1}{k}\sin kx + C\). Lời giải chi tiết: \(\begin{array}{l}\,\,\,\,\,\int\limits_0^\pi {\left( {2\cos x - \sin 2x} \right)dx} \\ = \left. {\left( {2\sin x + \dfrac{1}{2}\cos 2x} \right)} \right|_0^\pi \\ = 2\sin \pi + \dfrac{1}{2}\cos 2\pi - 2\sin 0 - \dfrac{1}{2}\cos 0\\ = \dfrac{1}{2} - \dfrac{1}{2} = 0\end{array}\) Chọn B. Câu hỏi 3 : Cho hàm số \(f\left( x \right)\) có đạo hàm trên đoạn \(\left[ { - 1;4} \right],\,\,f\left( 4 \right) = 2019,\,\,\int\limits_{ - 1}^4 {f'\left( x \right){\rm{d}}x} = 2020.\) Tính \(f\left( { - 1} \right)\)?
Đáp án: A Phương pháp giải: Sử dụng tính chất của tích phân để làm bài toán: \(\int\limits_a^b {f'\left( x \right)dx} = f\left( b \right) - f\left( a \right).\) Lời giải chi tiết: Theo đề bài ta có: \(\int\limits_{ - 1}^4 {f'\left( x \right)dx} = 2020\) \(\begin{array}{l} \Leftrightarrow f\left( 4 \right) - f\left( { - 1} \right) = 2020\\ \Leftrightarrow f\left( { - 1} \right) = f\left( 4 \right) - 2020\\ \Leftrightarrow f\left( { - 1} \right) = 2019 - 2020 = - 1.\end{array}\) Chọn A. Câu hỏi 4 : Tính tích phân \(I = \int\limits_0^2 {\left| {1 - x} \right|dx} \) ta được kết quả:
Đáp án: B Phương pháp giải: - Xét dấu của biểu thức \(1 - x\) trên \(\left[ {0;2} \right]\) và phá trị tuyệt đối. - Sử dụng các nguyên hàm cơ bản để tính tích phân. Lời giải chi tiết: \(\begin{array}{l}I = \int\limits_0^2 {\left| {1 - x} \right|dx} = \int\limits_0^1 {\left| {1 - x} \right|dx} + \int\limits_1^2 {\left| {1 - x} \right|dx} \\\,\,\,\, = \int\limits_0^1 {\left( {1 - x} \right)dx} - \int\limits_1^2 {\left( {1 - x} \right)dx} \\\,\,\,\, = \left. {\left( {x - \dfrac{{{x^2}}}{2}} \right)} \right|_0^1 - \left. {\left( {x - \dfrac{{{x^2}}}{2}} \right)} \right|_1^2\\\,\,\,\, = \dfrac{1}{2} - \left( {0 - \dfrac{1}{2}} \right) = 1\end{array}\). Chọn B. Câu hỏi 5 : Tính tích phân \(I=\int\limits_{0}^{\frac{\pi }{2}}{\frac{\sin 2x}{1+{{\sin }^{2}}x}dx}\) ta được:
Đáp án: A Phương pháp giải: Sử dụng phương pháp đặt ẩn phụ, đặt \(t={{\sin }^{2}}x\) Lời giải chi tiết: \(I=\int\limits_{0}^{\frac{\pi }{2}}{\frac{\sin 2x}{1+{{\sin }^{2}}x}dx}=I=\int\limits_{0}^{\frac{\pi }{2}}{\frac{2\sin x\cos x}{1+{{\sin }^{2}}x}dx}\) Đặt \(t={{\sin }^{2}}x\Leftrightarrow dt=2\sin x\cos xdx\). Đổi cận \(\left\{ \begin{array}{l}x = 0 \Leftrightarrow t = 0\\x = \frac{\pi }{2} \Leftrightarrow t = 1\end{array} \right.,\) khi đó ta có: \(I = \int\limits_0^1 {\frac{{dt}}{{1 + t}}} = \left. {\ln \left| {1 + t} \right|} \right|_0^1 = \ln 2 - \ln 1 = \ln 2\) Chọn A. Câu hỏi 6 : Tính tích phân \(I=\int\limits_{1}^{2}{\frac{{{x}^{2}}+2\ln x}{x}dx}\) ta được:
Đáp án: B Phương pháp giải: Sử dụng phương pháp đăt ẩn phụ, đặt \(t=\ln x\) Lời giải chi tiết: Đặt \(t=\ln x\Leftrightarrow dt=\frac{dx}{x}\) và \(x={{e}^{t}}\) Đổi cận \(\left\{ \begin{array}{l}x = 1 \Leftrightarrow t = 0\\x = 2 \Leftrightarrow t = \ln 2\end{array} \right.\), khi đó \(I=\int\limits_{1}^{2}{\frac{{{x}^{2}}+2\ln x}{x}dx}=\int\limits_{0}^{\ln 2}{\left( {{e}^{2t}}+2t \right)dt}=\left. \left( \frac{1}{2}{{e}^{2t}}+{{t}^{2}} \right) \right|_{0}^{\ln 2}=2+{{\ln }^{2}}2-\frac{1}{2}=\frac{3}{2}+{{\ln }^{2}}2\) Chọn B. Câu hỏi 7 : Biết \(f(x)\) là hàm liên tục trên \(\mathbb{R}\) và \(\int\limits_{0}^{9}{f(x)dx=9}\). Khi đó giá trị của \(\int\limits_{1}^{4}{f(3x-3)dx}\) là
Đáp án: B Phương pháp giải: Tính tích phân bằng phương pháp đổi biến. Lời giải chi tiết: Đặt \(3x-3=y\Rightarrow 3dx=dy\Leftrightarrow dx=\frac{dy}{3}\) Đổi cận:
\(I=\int\limits_{1}^{4}{f(3x-3)dx}=\frac{1}{3}\int\limits_{0}^{9}{f(y)dy}=\frac{1}{3}\int\limits_{0}^{9}{f(x)dx=\frac{1}{3}.9=3}\) Chọn: B. Câu hỏi 8 : Tích phân \(I=\int\limits_{1}^{e}{\frac{dx}{x-3}}\) bằng:
Đáp án: A Phương pháp giải: \(\int{\frac{1}{ax+b}dx}=\frac{1}{a}\ln \left| ax+b \right|+C\) Lời giải chi tiết: \(I=\int\limits_{1}^{e}{\frac{dx}{x-3}}=\left. \ln \left| x-3 \right| \right|_{1}^{e}=\ln \left| e-3 \right|-\ln 2=\ln \frac{3-e}{2}\) Chọn A. Câu hỏi 9 : Biết \(\int\limits_{1}^{3}{\frac{1}{2x+3}dx}=m\ln 5+n\ln 3\,\,\left( m,n\in R \right)\). Tính \(P=m-n\)
Đáp án: D Phương pháp giải: \(\int{\frac{1}{ax+b}dx}=\frac{1}{a}\ln \left| ax+b \right|+C\) Lời giải chi tiết: \(\begin{array}{l} Chọn D. Câu hỏi 10 : Tính tích phân \(\int\limits_{0}^{1}{\frac{dx}{{{x}^{2}}-x-12}}\)
Đáp án: D Phương pháp giải: \(\frac{1}{{{x}^{2}}-x-12}=\frac{1}{\left( x-4 \right)\left( x+3 \right)}=\frac{A}{x-4}+\frac{B}{x+3}\) Lời giải chi tiết: Ta có : \(\frac{1}{{{x}^{2}}-x-12}=\frac{1}{\left( x-4 \right)\left( x+3 \right)}=\frac{1}{7}\left( \frac{1}{x-4}-\frac{1}{x+3} \right)\) \(\Rightarrow I=\frac{1}{7}\int\limits_{0}^{1}{\left( \frac{1}{x-4}-\frac{1}{x+3} \right)dx}=\left. \frac{1}{7}\ln \left| \frac{x-4}{x+3} \right| \right|_{0}^{1}=\frac{1}{7}\left( \ln \frac{3}{4}-\ln \frac{4}{3} \right)=\frac{1}{7}\ln \frac{9}{16}\) Chọn D. Câu hỏi 11 : Cho \(\int\limits_{0}^{1}{\left( \frac{1}{x+1}-\frac{1}{x+2} \right)dx}=a\ln 2+b\ln 3\) với a, b là các số nguyên. Mệnh đề nào dưới đây đúng ?
Đáp án: D Phương pháp giải: \(\int{\frac{1}{ax+b}dx}=\frac{1}{a}\ln \left| ax+b \right|+C\) Lời giải chi tiết: \(\begin{array}{l}\int\limits_0^1 {\left( {\frac{1}{{x + 1}} - \frac{1}{{x + 2}}} \right)dx} = \left. {\left( {\ln \left| {x + 1} \right| - \ln \left| {x + 2} \right|} \right)} \right|_0^1 = \left. {\ln \left| {\frac{{x + 1}}{{x + 2}}} \right|} \right|_0^1 = \ln \frac{2}{3} - \ln \frac{1}{2} = \ln 2 - \ln 3 + \ln 2 = 2\ln 2 - \ln 3\\ \Rightarrow \left\{ \begin{array}{l}a = 2\\b = - 1\end{array} \right. \Rightarrow a + 2b = 2 - 2 = 0\end{array}\) Chọn D. Câu hỏi 12 : Tính tích phân \(I = \int\limits_0^2 {{x^2}\sqrt {{x^3} + 1} dx} \)
Đáp án: C Phương pháp giải: Đặt ẩn phụ \(t = \sqrt {{x^3} + 1} \) Lời giải chi tiết: Đặt \(t = \sqrt {{x^3} + 1} \Leftrightarrow {t^2} = {x^3} + 1 \Leftrightarrow 2tdt = 3{x^2}dx \Leftrightarrow {x^2}dx = {2 \over 3}tdt\) Đổi cận \(\left\{ \matrix{ x = 0 \Rightarrow t = 1 \hfill \cr x = 2 \Rightarrow t = 3 \hfill \cr} \right.\), khi đó ta có: \(I = \int\limits_1^3 {{{2{t^2}} \over 3}dt} = \left. {{2 \over 3}.{{{t^3}} \over 3}} \right|_1^3 = 6 - {2 \over 9} = {{52} \over 9}\) Chọn C. Câu hỏi 13 : Biến đổi \(\int\limits_0^3 {{x \over {1 + \sqrt {1 + x} }}dx} \) thành \(\int\limits_1^2 {f\left( t \right)dt} \) , với \(t = \sqrt {1 + x} \). Khi đó \(f\left( t \right)\) là hàm số nào trong các hàm số sau đây?
Đáp án: A Phương pháp giải: Đặt \(t = \sqrt {1 + x} \) Lời giải chi tiết: Đặt \(t = \sqrt {1 + x} \Leftrightarrow {t^2} = 1 + x \Leftrightarrow 2tdt = dx\) và \(x = {t^2} - 1\), đổi cận \(\left\{ \matrix{ x = 0 \Rightarrow t = 1 \hfill \cr x = 3 \Rightarrow t = 2 \hfill \cr} \right.\), khi đó ta có: \(I = \int\limits_1^2 {{{{t^2} - 1} \over {1 + t}}2tdt} = \int\limits_1^2 {2t\left( {t - 1} \right)dt} = \int\limits_1^2 {\left( {2{t^2} - 2t} \right)dt} \Rightarrow f\left( t \right) = 2{t^2} - 2t\). Chọn A. Câu hỏi 14 : Nếu \(\int\limits_{0}^{1}{f\left( x \right)\,\text{d}x}=5\) và \(\int\limits_{1}^{2}{f\left( x \right)\,\text{d}x}=2\) thì \(\int\limits_{0}^{2}{f\left( x \right)\,\text{d}x}\) bằng
Đáp án: C Phương pháp giải: Sử dụng lý thuyết tích phân \(\int\limits_{a}^{c}{f\left( x \right)\,\text{d}x}+\int\limits_{c}^{b}{f\left( x \right)\,\text{d}x}=\int\limits_{a}^{b}{f\left( x \right)\,\text{d}x}.\) Lời giải chi tiết: Ta có \(\int\limits_{0}^{2}{f\left( x \right)\,\text{d}x}=\int\limits_{0}^{1}{f\left( x \right)\,\text{d}x}+\int\limits_{1}^{2}{f\left( x \right)\,\text{d}x}=5+2=7.\) Chọn C Câu hỏi 15 : Cho \(I = \int\limits_{{\pi \over 6}}^{{\pi \over 4}} {{{dx} \over {{{\cos }^2}x{{\sin }^2}x}}} = a + b\sqrt 3 \) với a, b là số hữu tỉ. Tính giá trị a – b.
Đáp án: B Phương pháp giải: Sử dụng công thức nhân đôi \(\sin 2x = 2\sin x\cos x\) Lời giải chi tiết: \(I = \int\limits_{{\pi \over 6}}^{{\pi \over 4}} {{{dx} \over {{{\cos }^2}x{{\sin }^2}x}}} = \int\limits_{{\pi \over 6}}^{{\pi \over 4}} {{{4dx} \over {{{\sin }^2}2x}}} = \left. { - 2\cot 2x} \right|_{{\pi \over 6}}^{{\pi \over 4}} = - 2\left( {0 - {1 \over {\sqrt 3 }}} \right) = {2 \over {\sqrt 3 }} = {{2\sqrt 3 } \over 3} \Rightarrow \left\{ \matrix{ a = 0 \hfill \cr b = {2 \over 3} \hfill \cr} \right. \Rightarrow a - b = - {2 \over 3}\) Chọn B. Câu hỏi 16 : Tính tích phân \(I = \int\limits_{ - {\pi \over 2}}^{{\pi \over 6}} {\left( {\sin 2x - \cos 3x} \right)dx} \)
Đáp án: C Phương pháp giải: Sử dụng bảng nguyên hàm cơ bản. Lời giải chi tiết: \(I = \int\limits_{ - {\pi \over 2}}^{{\pi \over 6}} {\left( {\sin 2x - \cos 3x} \right)dx} = \left. {\left( { - {{\cos 2x} \over 2} - {{\sin 3x} \over 3}} \right)} \right|_{ - {\pi \over 2}}^{{\pi \over 6}} = {{ - 7} \over {12}} - {1 \over 6} = - {3 \over 4}\) Chọn C. Câu hỏi 17 : Tính \(I=\int\limits_{0}^{1}{{{e}^{3x}}dx}\).
Đáp án: C Phương pháp giải: \(\int\limits_{{}}^{{}}{{{e}^{kx}}dx}=\frac{1}{k}{{e}^{kx}}+C\) Lời giải chi tiết: \(I=\int\limits_{0}^{1}{{{e}^{3x}}dx}=\frac{1}{3}\left. {{e}^{3x}} \right|_{0}^{1}=\frac{{{e}^{3}}-1}{3}\) Chọn: C Câu hỏi 18 : Cho hàm số \(f\left( x \right)\) liên tục trên khoảng \(\left( a;c \right),\) \(a<b<c\) và \(\int\limits_{a}^{b}{f\left( x \right)\,\text{d}x}=5,\,\,\int\limits_{c}^{b}{f\left( x \right)\,\text{d}x}=1.\) Tính tích phân \(I=\int\limits_{a}^{c}{f\left( x \right)\,\text{d}x}.\)
Đáp án: A Phương pháp giải: Sử dụng tích chất của tích phân : Với \(a<b<c\) ta có : \(\int\limits_{a}^{c}{f\left( x \right)dx=}\int\limits_{a}^{b}{f\left( x \right)dx}+\int\limits_{b}^{c}{f\left( x \right)dx.}\) Lời giải chi tiết: Ta có \(I=\int\limits_{a}^{c}{f\left( x \right)\,\text{d}x}=\int\limits_{a}^{b}{f\left( x \right)\,\text{d}x}+\int\limits_{b}^{c}{f\left( x \right)\,\text{d}x}=\int\limits_{a}^{b}{f\left( x \right)\,\text{d}x}-\int\limits_{c}^{b}{f\left( x \right)\,\text{d}x}=5-1=4.\) Chọn A Câu hỏi 19 : Tích phân \(I=\int\limits_{0}^{1}{{{e}^{x\,+\,1}}\,\text{d}x}\) bằng
Đáp án: B Phương pháp giải: Đổi biến số hoặc bấm máy tính Lời giải chi tiết: Ta có \(I=\int\limits_{0}^{1}{{{e}^{x\,+\,1}}\,\text{d}x}=\,\int\limits_{0}^{1}{{{e}^{x\,+\,1}}\,\text{d}\left( x+1 \right)}=\left. {{e}^{x\,+\,1}} \right|_{0}^{1}={{e}^{2}}-e.\) Chọn B Câu hỏi 20 : Tích phân \(\int\limits_{1}^{2}{{{\left( x+3 \right)}^{2}}dx}\) bằng
Đáp án: B Phương pháp giải: Lời giải chi tiết: Câu hỏi 21 : Tích phân \(\int\limits_0^1 {x\left( {{x^2} + 3} \right)\,{\rm{d}}x} \) bằng
Đáp án: B Phương pháp giải: Lời giải chi tiết: Câu hỏi 22 : Cho \(\int\limits_0^1 {f\left( x \right)dx} = 2\) và \(\int\limits_0^1 {g\left( x \right)dx} = 5\), khi đó \(\int\limits_0^1 {\left[ {f\left( x \right) - 2g\left( x \right)} \right]dx} \) bằng
Đáp án: C Phương pháp giải: Sử dụng tính chất tích phân \(\int\limits_a^b {\left[ {\alpha f\left( x \right) \pm \beta g\left( x \right)} \right]dx} = \alpha \int\limits_a^b {f\left( x \right)dx} \pm \beta \int\limits_a^b {g\left( x \right)dx} \)
Lời giải chi tiết: Ta có: \(\int\limits_0^1 {\left[ {f\left( x \right) - 2g\left( x \right)} \right]dx} = \int\limits_0^1 {f\left( x \right)dx} - 2\int\limits_0^1 {g\left( x \right)dx} = 2 - 2.5 = - 8\) CHỌN C Câu hỏi 23 : Cho \(f\left( x \right),g\left( x \right)\) là hai hàm số liên tục trên \(\mathbb{R}\). Chọn mệnh đề sai trong các mệnh đề sau
Đáp án: A Phương pháp giải: Sử dụng tính chất tích phân. Lời giải chi tiết: Ta có \(\left\{ \begin{array}{l}\int\limits_a^a {f\left( x \right)dx = 0} ;\,\,\,\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^b {f\left( y \right)dy} ;\\\int\limits_a^b {\left( {f\left( x \right) - g\left( x \right)} \right)dx} = \int\limits_a^b {f\left( x \right)dx - \int\limits_a^b {g\left( x \right)dx} } \end{array} \right.\) nên B, C, D đúng. A sai vì tích phân một tích không bằng tích các tích phân. Chọn A. Câu hỏi 24 : Cho hàm số \(y = f\left( x \right),\,\,y = g\left( x \right)\) liên tục trên \(\left[ {a;b} \right]\) và số thực \(k\) tùy ý. Trong các khẳng định sau, khẳng định nào sai?
Đáp án: B Phương pháp giải: Sử dụng các tính chất của tích phân: \(\int\limits_a^a {kf\left( x \right)dx} = 0\) \(\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} + \int\limits_a^b {g\left( x \right)dx} \) \(\int\limits_a^b {f\left( x \right)dx} = - \int\limits_b^a {f\left( x \right)dx} \) Lời giải chi tiết: Dựa vào các đáp án ta dễ dàng nhận thấy các đáp án A, C, D đúng, đáp án B sai. Chọn B. Câu hỏi 25 : Cho \(\int\limits_1^2 {f\left( x \right)dx} = 2\) và \(\int\limits_1^2 {2g\left( x \right)dx} = 8\). Khi đó \(\int\limits_1^2 {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} \) bằng:
Đáp án: B Phương pháp giải: Sử dụng tính chất tích phân: \(\int\limits_a^b {f\left( x \right)dx} + \int\limits_a^b {g\left( x \right)dx} = \int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} \). Lời giải chi tiết: Ta có: \(\int\limits_1^2 {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} = \int\limits_1^2 {f\left( x \right)dx} + \int\limits_1^2 {g\left( x \right)dx} = 2 + 4 = 6\). Chọn B. Câu hỏi 26 : Cho các hàm số \(f\left( x \right)\) và \(F\left( x \right)\) liên tục trên \(\mathbb{R}\) thỏa \(F'\left( x \right) = f\left( x \right),\forall x \in \mathbb{R}\). Tính \(\int\limits_0^1 {f\left( x \right)dx} \) biết \(F\left( 0 \right) = 2,\,F\left( 1 \right) = 5\).
Đáp án: C Phương pháp giải: Sử dụng công thức \(\int\limits_a^b {F'\left( x \right)dx} = F\left( b \right) - F\left( a \right)\). Lời giải chi tiết: Ta có: \(\int\limits_0^1 {f\left( x \right)dx} = \int\limits_0^1 {F'\left( x \right)dx} = F\left( 1 \right) - F\left( 0 \right) = 5 - 2 = 3\). Chọn: C Câu hỏi 27 : Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và a là số dương. Trong các khẳng định sau, khẳng định nào đúng?
Đáp án: A Phương pháp giải: Sử dụng tính chất của tích phân: \(\int\limits_a^a {f\left( x \right)dx} = 0\) Lời giải chi tiết: \(\int\limits_a^a {f\left( x \right)dx} = 0\). Chọn: A Câu hỏi 28 : Để tính tích phân \(I = \int\limits_0^{\dfrac{\pi }{2}} {{e^{\sin x}}\cos xdx} \) ta chọn cách đặt nào sau đây cho phù hợp ?
Đáp án: D Phương pháp giải: Tính tích phân bằng phương pháp đặt ẩn phụ. Lời giải chi tiết: Đặt \(t = \sin x \Rightarrow dt = \cos xdx\). Đổi cận: \(\left\{ \begin{array}{l}x = 0 \Rightarrow t = 0\\x = \dfrac{\pi }{2} \Rightarrow t = 1\end{array} \right.\). Ta có: \(I = \int\limits_0^{\dfrac{\pi }{2}} {{e^{\sin x}}\cos xdx} = \int\limits_0^1 {{e^t}dt} = \left. {{e^t}} \right|_0^1 = e - 1\). Chọn D. Câu hỏi 29 : Giá trị của \(\int\limits_0^1 {\pi x{e^x}dx} \) là:
Đáp án: A Phương pháp giải: Sử dụng MTCT. Lời giải chi tiết:
Sử dụng MTCT ta có: Chọn A. Câu hỏi 30 : Tính tích phân \(I = \int\limits_1^e {\dfrac{{3\ln x + 1}}{x}{\rm{d}}x} \). Nếu đặt \(t = \ln x\) thì
Đáp án: D Phương pháp giải: Tính \(dt\), đổi cận và thay vào tính \(I\). Lời giải chi tiết: Đặt \(t = \ln x\)\( \Rightarrow {\rm{d}}t = \dfrac{{{\rm{d}}x}}{x}\). Đổi cận: \(x = 1 \Rightarrow t = 0;x = e \Rightarrow t = 1\) Vậy \(I = \int\limits_0^1 {\left( {3t + 1} \right){\rm{d}}t} \) Chọn D. Câu hỏi 31 : Khẳng định nào dưới đây là đúng?
Đáp án: C Phương pháp giải: Sử dụng các tính chất: \(\int\limits_{}^{} {kf\left( x \right)dx} = k\int\limits_{}^{} {f\left( x \right)dx} \). Lời giải chi tiết: Khẳng định đúng là \(\int\limits_{ - 2}^2 {2f\left( x \right)dx} = 2\int\limits_{ - 2}^2 {f\left( x \right)dx} \). Chọn C. Câu hỏi 32 : Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(\int\limits_0^4 {f\left( x \right)dx} = 10,\,\,\int\limits_3^4 {f\left( x \right)dx} = 4\). Tích phân \(\int\limits_0^3 {f\left( x \right)dx} \) bằng:
Đáp án: D Phương pháp giải: Sử dụng tính chất của tích phân \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \). Lời giải chi tiết: \(\int\limits_0^3 {f(x)dx} \)\( = \int\limits_0^4 {f\left( x \right)} dx + \int\limits_4^3 {f\left( x \right)} dx = \int\limits_0^4 {f\left( x \right)} dx - \int\limits_3^4 {f\left( x \right)} dx\)\( = 10 - 4 = 6\). Chọn: D Câu hỏi 33 : Với \(f\left( x \right)\) là hàm số tùy ý liên tục trên \(\mathbb{R},\) chọn mệnh đề sai trong các mệnh đề sau:
Đáp án: A Phương pháp giải: Sử dụng các tính chất cơ bản của tích phân để chọn đáp án đúng: \(\begin{array}{l}\int\limits_a^b {kf\left( x \right)dx} = k\int\limits_a^b {f\left( x \right)dx} \,\,\,\left( {k \in \mathbb{R}} \right)\\\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \\\int\limits_a^b {f\left( x \right)dx} = - \int\limits_b^a {f\left( x \right)dx} \end{array}\) Lời giải chi tiết: Sử dụng các tính chất cơ bản của tích phân ta thấy chỉ có đáp án A sai. Chọn A. Câu hỏi 34 : Cho hàm số \(f\left( x \right)\) thỏa mãn \(\int\limits_1^3 {f\left( x \right)dx} = 5\) và \(\int\limits_{ - 1}^3 {f\left( x \right)dx} = 1\). Tính tích phân \(I = \int\limits_{ - 1}^1 {f\left( x \right)dx} \).
Đáp án: A Phương pháp giải: Sử dụng tính chất tích phân \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \). Lời giải chi tiết: \(I = \int\limits_{ - 1}^1 {f\left( x \right)dx} = \int\limits_{ - 1}^3 {f\left( x \right)dx} + \int\limits_3^1 {f\left( x \right)dx} = \int\limits_{ - 1}^3 {f\left( x \right)dx} - \int\limits_1^3 {f\left( x \right)dx} = 1 - 5 = - 4\). Chọn: A Câu hỏi 35 : Cho \(\int\limits_0^1 {f\left( x \right)dx} = 3\) và \(\int\limits_1^2 {f\left( x \right)dx = 2.} \) Khi đó \(\int\limits_0^2 {f\left( x \right)dx} \) bằng
Đáp án: C Phương pháp giải: Sử dụng tính chất tích phân: \(\int\limits_a^b {f\left( x \right)dx + } \int\limits_b^c {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} \) Lời giải chi tiết: Ta có \(\int\limits_0^1 {f\left( x \right)dx + } \int\limits_1^2 {f\left( x \right)dx} = \int\limits_0^2 {f\left( x \right)dx} \Leftrightarrow \int\limits_0^2 {f\left( x \right)dx} = 2 + 3 = 5.\) Chọn C. Câu hỏi 36 : Giả sử \(f\left( x \right)\) và \(g\left( x \right)\) là các số bất kì liên tục trên \(\mathbb{R}\) và \(a,\,b,\,c\) là các số thực. Mệnh dề nào sau đây sai?
Đáp án: C Phương pháp giải: Sử dụng các tính chất cơ bản của tích phân để chọn đáp án đúng: \(\begin{array}{l}\int\limits_a^b {kf\left( x \right)dx} = k\int\limits_a^b {f\left( x \right)dx} \,\,\,\left( {k \in \mathbb{R}} \right)\\\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \\\int\limits_a^b {f\left( x \right)dx} = - \int\limits_b^a {f\left( x \right)dx} \end{array}\) Lời giải chi tiết: Dựa vào các tính chất cơ bản của tích phân ta có: \(\int\limits_a^b {f\left( x \right)dx} + \int\limits_b^c {f\left( x \right)dx} + \int\limits_c^a {f\left( x \right)dx} = \int\limits_a^a {f\left( x \right)dx} = 0 \Rightarrow \) đáp án A đúng. \(\int\limits_a^b {cf\left( x \right)dx} = c\int\limits_a^b {f\left( x \right)dx} \Rightarrow \) đáp án B đúng. \(\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} + \int\limits_a^b {g\left( x \right)dx} = \int\limits_a^b {f\left( x \right)dx} - \int\limits_a^b {g\left( x \right)dx} + \int\limits_a^b {g\left( x \right)dx} = \int\limits_a^b {f\left( x \right)dx} \Rightarrow \)đáp án D đúng. Chọn C. Câu hỏi 37 : Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) liên tục liên tục trên đoạn \(\left[ {a;b} \right]\). Biết \(f\left( a \right) = 5\) và \(\int\limits_a^b {f'\left( x \right)dx} = 2\sqrt 5 \), tính \(f\left( b \right)\).
Đáp án: B Phương pháp giải: Sử dụng công thức tích phân \(\int\limits_a^b {f'\left( x \right)dx} = f\left( b \right) - f\left( a \right)\). Lời giải chi tiết: Ta có: \(\int\limits_a^b {f'\left( x \right)dx} = f\left( b \right) - f\left( a \right)\)\( \Rightarrow f\left( b \right) - f\left( a \right) = 2\sqrt 5 \) \( \Rightarrow f\left( b \right) - 5 = 2\sqrt 5 \) \( \Leftrightarrow f\left( b \right) = 5 + 2\sqrt 5 = \sqrt 5 \left( {\sqrt 5 + 2} \right)\) Chọn B. Câu hỏi 38 : Tính \(I = \int\limits_{ - 1}^2 {6{x^2}dx} \).
Đáp án: A Phương pháp giải: Sử dụng công thức: \(\int\limits_a^b {{x^n}dx} = \left. {\dfrac{{{x^{n + 1}}}}{{n + 1}}} \right|_a^b,\,\,\left( {n \ne - 1} \right)\). Lời giải chi tiết: Ta có: \(I = \int\limits_{ - 1}^2 {6{x^2}dx} = \left. {2{x^3}} \right|_{ - 1}^2 = 16 + 2 = 18\). Chọn: A Câu hỏi 39 : Tính \(I = \int\limits_0^1 {{e^x}} dx\).
Đáp án: B Phương pháp giải: Sử dụng công thức nguyên hàm cơ bản. Lời giải chi tiết: \(I = \int\limits_0^1 {{e^x}} dx = \left. {{e^x}} \right|_0^1 = e - 1\) Chọn: B Câu hỏi 40 : Cho \(\int\limits_1^5 {f\left( x \right)} dx = a\) và \(\int\limits_1^{2018} {f\left( x \right)} dx = b\). Khi đó \(\int\limits_5^{2018} {f\left( x \right)} dx\) bằng
Đáp án: A Phương pháp giải: Sử dụng tính chất tích phân: \(\int\limits_a^b {f\left( x \right)} dx = \int\limits_a^c {f\left( x \right)} dx + \int\limits_c^b {f\left( x \right)} dx\). Lời giải chi tiết: Ta có: \(\int\limits_5^{2018} {f\left( x \right)} dx = \int\limits_5^1 {f\left( x \right)} dx + \int\limits_1^{2018} {f\left( x \right)} dx = - \int\limits_1^5 {f\left( x \right)} dx + \int\limits_1^{2018} {f\left( x \right)} dx = - a + b\). Chọn: A Câu hỏi 41 : Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên đoạn \(\left[ { - 2;1} \right]\) và \(f\left( { - 2} \right) = 3,\,f\left( 1 \right) = 7\). Tính \(I = \int\limits_{ - 2}^1 {f'\left( x \right)dx} \).
Đáp án: D Phương pháp giải: \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) \Rightarrow \int\limits_a^b {f\left( x \right)dx} = F\left( b \right) - F\left( a \right)\). Lời giải chi tiết: \(I = \int\limits_{ - 2}^1 {f'\left( x \right)dx} = f\left( 1 \right) - f\left( { - 2} \right) = 7 - 3 = 4\). Chọn: D Câu hỏi 42 : Giả sử \(\int\limits_a^b {f\left( x \right)dx} = 2,\,\,\int\limits_c^b {f\left( x \right)dx} = 3\) với \(a < b < c\) thì \(\int\limits_a^c {f\left( x \right)dx} \) bằng:
Đáp án: D Phương pháp giải: \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} \) Lời giải chi tiết: \(\int\limits_a^c {f\left( x \right)dx} = \int\limits_a^b {f\left( x \right)dx} - \int\limits_c^b {f\left( x \right)dx} = 2 - 3 = - 1\). Chọn: D Câu hỏi 43 : Cho hai hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và \(a < c < b\). Mệnh đề nào dưới đây sai?
Đáp án: C Phương pháp giải: Sử dụng tính chất của tích phân. Lời giải chi tiết: Dễ thấy A, B, D đúng. C sai: \(\int\limits_a^b {\dfrac{{f\left( x \right)}}{{g\left( x \right)}}dx} \ne \dfrac{{\int\limits_a^b {f\left( x \right)dx} }}{{\int\limits_a^b {g\left( x \right)dx} }}\) Chọn C Câu hỏi 44 : Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) trên đoạn \(\left[ {a;b} \right]\). Mệnh đề nào dưới đây đúng?
Đáp án: B Phương pháp giải: Sử dụng công thức tích phân Leibnitz: \(\int\limits_a^b {f\left( x \right)dx} = F\left( b \right) - F\left( a \right)\) với \(F'\left( x \right) = f\left( x \right)\). Lời giải chi tiết: Do \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) nên \(\int\limits_a^b {f\left( x \right)dx} = F\left( b \right) - F\left( a \right)\). Chọn B Câu hỏi 45 : Cho \(f\left( x \right)\) và \(g\left( x \right)\) là các hàm số liên tục bất kì trên đoạn \(\left[ {a;\,\,b} \right].\) Mênh đề nào sau đây đúng?
Đáp án: B Phương pháp giải: Sử dụng các tính chất của tích phân: \(\int\limits_a^b {\left[ {f\left( x \right) \pm g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} \pm \int\limits_a^b {g\left( x \right)dx} .\) Lời giải chi tiết: Sử dụng các tính chất của tích phân: \(\int\limits_a^b {\left[ {f\left( x \right) \pm g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} \pm \int\limits_a^b {g\left( x \right)dx} .\) Chọn B. Câu hỏi 46 : Cho các số thực a, b \((a<b)\). Nếu hàm số \(y=f(x)\) có đạo hàm là hàm liên tục trên \(\mathbb{R}\) thì
Đáp án: B Phương pháp giải: Lời giải chi tiết: Chọn B. Câu hỏi 47 : Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(f\left( 0 \right) = 1,f'\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(\int\limits_0^3 {f'\left( x \right)dx} = 9\). Giá trị của \(f\left( 3 \right)\) là
Đáp án: C Phương pháp giải: Sử dụng công thức tích phân \(\int\limits_a^b {f'\left( x \right)dx} = f\left( b \right) - f\left( a \right)\). Lời giải chi tiết: Ta có: \(\int\limits_0^3 {f'\left( x \right)dx} = 9 = f\left( 3 \right) - f\left( 0 \right)\)\( \Rightarrow f\left( 3 \right) = 9 + f\left( 0 \right) = 9 + 1 = 10\). Chọn C. Câu hỏi 48 : Cho hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\) liên tục trên \(\left[ {a;b} \right]\) và số thực \(k\) tùy ý. Trong các phát biểu sau, phát biểu nào sai?
Đáp án: D Phương pháp giải: Sử dụng các tính chất của tích phân. Lời giải chi tiết: Dễ thấy mệnh đề sai là: \(\int\limits_a^b {xf\left( x \right){\rm{d}}x} = x\int\limits_a^b {f\left( x \right){\rm{d}}x} \). Chọn D. Câu hỏi 49 : Cho các hàm số \(f\left( x \right),\,\,\,g\left( x \right)\) liên tục trên tập xác định. Tìm mệnh đề sai?
Đáp án: C Phương pháp giải: Dựa vào tính chất tích phân. Lời giải chi tiết: Mệnh đề sai là C. Mệnh đề đúng phải là: \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} \,\,\forall k \in \mathbb{R},\,\,k \ne 0\). Chọn C. Câu hỏi 50 : Tính tích phân \(I = \int\limits_0^1 {\left| {x - 2} \right|dx} \) ta được kết quả:
Đáp án: C Phương pháp giải: - Xét dấu của biểu thức \(x - 2\) trên \(\left[ {0;1} \right]\) và phá trị tuyệt đối. - Sử dụng các nguyên hàm cơ bản để tính tích phân. Lời giải chi tiết: Với \(x \in \left[ {0;1} \right]\) thì \(x - 2 < 0\), do đó \(\left| {x - 2} \right| = 2 - x\). Khi đó ta có: \(I = \int\limits_0^1 {\left| {x - 2} \right|dx} = \int\limits_0^1 {\left( {2 - x} \right)dx} \)\( = \left. {\left( {2x - \dfrac{{{x^2}}}{2}} \right)} \right|_0^1 = 2 - \dfrac{1}{2} = \dfrac{3}{2}\). Chọn C. Quảng cáo
|