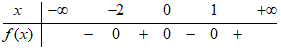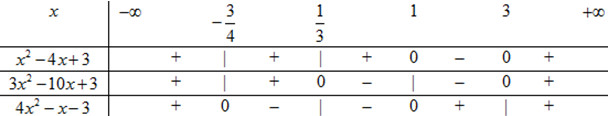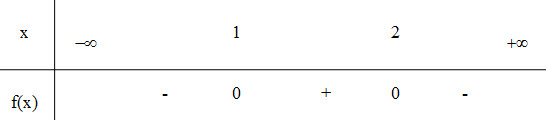50 bài tập trắc nghiệm bất phương trình mức độ nhận biết, thông hiểuLàm bàiQuảng cáo
Câu hỏi 1 : Điều kiện của bất phương trình \(2\sqrt {x + 2} > 7{x^2} + \frac{1}{{x - 1}}\) là:
Đáp án: C Phương pháp giải: \(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0\) \(\frac{1}{{g\left( x \right)}}\) xác định \( \Leftrightarrow g\left( x \right) \ne 0\) Lời giải chi tiết: Phương trình xác định \( \Leftrightarrow \left\{ \begin{array}{l}x + 2 \ge 0\\x - 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\x \ne 1\end{array} \right..\) Chọn C. Câu hỏi 2 : Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x - y + 2 \ge 0\\ - x - 2y - 2 < 0\end{array} \right.\) là miền chứa điểm nào trong các điểm sau?
Đáp án: A Phương pháp giải: Thay tọa độ từng điểm vào hệ bất phương trình để kiểm chứng. Lời giải chi tiết: Thay tọa độ điểm \(M\left( {1;\;1} \right)\) vào hệ BPT ta có: \(\left\{ \begin{array}{l}2.1 - 1 + 2 = 3 \ge 0\\ - 1 - 2.1 - 2 = - 5 < 0\end{array} \right.\) Vậy điểm \(M\left( {1;1} \right)\) thuộc miền nghiệm của hệ BPT \(\left\{ \begin{array}{l}2x - y + 2 \ge 0\\ - x - 2y - 2 < 0\end{array} \right..\) Chọn A. Câu hỏi 3 : Điểm \({M_0}\left( {1;0} \right)\) thuộc miền nghiệm của hệ bất phương trình:
Đáp án: C Phương pháp giải: Thay tọa độ điểm vào từng hệ bất phương trình để kiểm chứng. Lời giải chi tiết: Thay tọa độ điểm \(M\left( {1;\;0} \right)\) vào hệ BPT ta có: \(\left\{ \begin{array}{l}2.1 - 0 = 2 \le 3\\10.1 + 5.0 = 10 > 8\end{array} \right. \Rightarrow \) Chọn C. Vậy điểm \({M_0}\left( {1;0} \right)\) thuộc miền nghiệm của hệ BPT \(\left\{ \begin{array}{l}2x - y \le 3\\10x + 5y > 8\end{array} \right.\) Chọn C. Câu hỏi 4 : Tìm điều kiện xác định của bất phương trình \(\sqrt {2 - x} + x < 2 + \sqrt {1 - 2x} \).
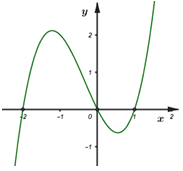
Đáp án: C Phương pháp giải: \(\sqrt A \) xác định \( \Leftrightarrow A \ge 0\). Lời giải chi tiết: ĐKXĐ: \(\left\{ \begin{array}{l}2 - x \ge 0\\1 - 2x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 2\\x \le \dfrac{1}{2}\end{array} \right. \Leftrightarrow x \le \dfrac{1}{2}\). Vậy \(x \in \left( { - \infty ;\dfrac{1}{2}} \right]\). Chọn C. Câu hỏi 5 : Cho hàm số \(y = f\left( x \right)\) có đồ thị như bình bên. Bảng xét dấu của \(f\left( x \right)\) là bảng nào sau đây ?
Đáp án: B Phương pháp giải: Nhìn vào đồ thị để suy ra bảng xét dấu của hàm số. Lời giải chi tiết: Nhìn vào đồ thị ta thấy với \(x \in \left( { - \infty ; - 2} \right) \cup \left( {0;1} \right)\) thì \(f\left( x \right) < 0\), với \(x \in \left( { - 2;0} \right) \cup \left( {1; + \infty } \right)\) thì \(f\left( x \right) > 0\) Vậy B đúng. Chọn B. Câu hỏi 6 : Tập nghiệm của bất phương trình \(9\left( {x - \frac{1}{5}} \right) < 7 - 2x\) là
Đáp án: D Phương pháp giải: Giải bất phương trình bậc nhất một ẩn. Lời giải chi tiết: \(9\left( {x - \frac{1}{5}} \right) < 7 - 2x \Leftrightarrow 9x - \frac{9}{5} + 2x < 7\)\( \Leftrightarrow 11x < \frac{{44}}{5} \Leftrightarrow x < \frac{4}{5}.\) Chọn D. Câu hỏi 7 : Bất phương trình \(2{{x}^{2}}.3\text{x < 1}\) có bao nhiêu nghiệm nguyên?
Đáp án: B Phương pháp giải: Giải bất phương trình và tìm số nghiệm nguyên của nó Lời giải chi tiết: TXĐ: D = R Bất phương trình đã cho tương đương với \(6{{x}^{3}}<1\Leftrightarrow {{x}^{3}}<\frac{1}{6}\Leftrightarrow x<\frac{1}{\sqrt[3]{6}}\) Có vô số số nguyên x thỏa mãn bất phương trình Chọn đáp án B
Câu hỏi 8 : Tam thức \(f\left( x \right) = 3{x^2} + 2\left( {2m - 1} \right)x + m + 4\) dương với mọi \(x\) khi
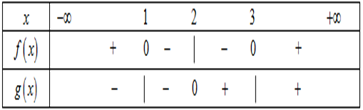
Đáp án: C Phương pháp giải: Sử dụng cho hàm số \(f\left( x \right) = a{x^2} + bx + c\) Khi đó \(f\left( x \right) > 0\,;\,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta ' = {{b'}^2} - ac < 0\end{array} \right.\) Lời giải chi tiết: Ta có \(f\left( x \right) = 3{x^2} + 2\left( {2m - 1} \right)x + m + 4\) Để \(f\left( x \right) > 0\,;\,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}3 > 0\left( {luon\,\,dung} \right)\\\Delta ' = {\left( {2m - 1} \right)^2} - 3\left( {m + 4} \right) < 0\end{array} \right. \Rightarrow 4{m^2} - 7m - 11 < 0 \Leftrightarrow - 1 < m < \dfrac{{11}}{4}\) Chọn: C Câu hỏi 9 : Cho \(f(x),g(x)\) là các hàm số xác định trên \(\mathbb{R}\), có bảng xét dấu như sau: Khi đó tập nghiệm của bất phương trình \(\frac{{f(x)}}{{g(x)}} \ge 0\) là
Đáp án: B Phương pháp giải: Cho \(f(x),g(x)\) là các hàm số xác định trên \(\mathbb{R}\) thì \(\frac{{f(x)}}{{g(x)}} \ge 0\,\,\left( {g\left( x \right) \ne 0} \right) \Leftrightarrow \)\(f\left( x \right)\) và \(g\left( x \right)\) cùng dấu hoặc \(f\left( x \right) = 0\) Lời giải chi tiết: Cho \(f(x),g(x)\) là các hàm số xác định trên \(\mathbb{R}\) thì \(\frac{{f(x)}}{{g(x)}} \ge 0\,\,\left( {g\left( x \right) \ne 0} \right) \Leftrightarrow \)\(f\left( x \right)\) và \(g\left( x \right)\) cùng dấu hoặc \(f\left( x \right) = 0\)\( \Leftrightarrow x \in \left[ {1;2} \right) \cup \left[ {3; + \infty } \right)\) Chọn B. Câu hỏi 10 : Tập nghiệm của bất phương trình \(\frac{{x + 1}}{{2 - x}} < 0\) là:
Đáp án: C Phương pháp giải: Lập bảng xét dấu để giải bất phương trình hoặc giải bất phương trình: \(\frac{{f\left( x \right)}}{{g\left( x \right)}} < 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}f\left( x \right) > 0\\g\left( x \right) < 0\end{array} \right.\\\left\{ \begin{array}{l}f\left( x \right) < 0\\g\left( x \right) > 0\end{array} \right.\end{array} \right..\) Lời giải chi tiết: \(\frac{{x + 1}}{{2 - x}} < 0\) ĐKXĐ: \(2 - x \ne 0 \Leftrightarrow x \ne 2\) Đặt \(f\left( x \right) = \frac{{x + 1}}{{2 - x}}\) . Ta có bảng: Vậy \(f\left( x \right) < 0 \Leftrightarrow \left[ \begin{array}{l}x < - 1\\x > 2\end{array} \right.\) \( \Rightarrow \) Tập nghiệm của phương trình là \(\left( { - \infty ; - 1} \right) \cup \left( {2; + \infty } \right)\) Chọn C. Câu hỏi 11 : Tập nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}3x + 1 > 2x + 7\\4x + 3 \le 2x + 21\end{array} \right.\)
Đáp án: C Phương pháp giải: Giải từng bất phương trình và kết hợp nghiệm. Lời giải chi tiết: \(\left\{ \begin{array}{l}3x + 1 > 2x + 7\\4x + 3 \le 2x + 21\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 6\\2x \le 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 6\\x \le 9\end{array} \right. \Leftrightarrow 6 < x \le 9.\) Vậy tập nghiệm của bất phương trình là \(\left( {6;9} \right].\) Chọn C. Câu hỏi 12 : Các giá trị của tham số \(m\) để bất phương trình \(\left( {{m^2} - 1} \right)x + m \ge 0\) có nghiệm là :
Đáp án: C Phương pháp giải: Xét từng trường hợp hệ số của \(x\) bằng 0, khác 0 Lời giải chi tiết: Khi \(m = 1 \Rightarrow 0 + 1 = 1 \ge 0 \Rightarrow \) bất phương trình có nghiệm. Khi \(m = - 1 \Rightarrow 0 - 1 = - 1 \ge 0 \Rightarrow \) bất phương trình vô nghiệm. Khi \(\left[ \begin{array}{l}m > 1\\m < - 1\end{array} \right. \Rightarrow x \ge \frac{m}{{1 - {m^2}}} \Rightarrow \) bất phương trình có nghiệm. Khi \( - 1 < m < 1 \Rightarrow x \le \frac{m}{{1 - {m^2}}} \Rightarrow \) bất phương trình có nghiệm. Vậy BPT có nghiệm \( \Leftrightarrow m \in \mathbb{R}\backslash \left\{ { - 1} \right\}.\) Chọn C. Câu hỏi 13 : Cho \(f\left( x \right) = -2{x^2} + \left( {m + 2} \right)x + m-4\). Tìm \(m\) để \(f\left( x \right)\) âm với mọi \(x.\)
Đáp án: C Phương pháp giải: Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) có biệt thức \(\Delta = {b^2} - 4ac\) - Nếu \(\Delta < 0\) thì với mọi \(x,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta = 0\) thì \(f\left( x \right)\) có nghiệm kép \(x = - \frac{b}{{2a}}\), với mọi \(x \ne - \frac{b}{{2a}},\,\,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta > 0\),\(f\left( x \right)\)có 2 nghiệm \({x_1},{x_2}\,\,\left( {{x_1} < {x_2}} \right)\) và luôn cùng dấu với hệ số a với mọi x ngoài khoảng \(\left( {{x_1};\,\,{x_2}} \right)\) và luôn trái dấu với hệ số a với mọi x trong khoảng \(\left( {{x_1};\,\,{x_2}} \right).\) Lời giải chi tiết: \(f\left( x \right) < 0 \Leftrightarrow -2{x^2} + \left( {m + 2} \right)x + m-4\) Ta có: \(\Delta = {\left( {m + 2} \right)^2} + 8\left( {m - 4} \right) = {m^2} + 12m - 28.\) \(\begin{array}{l} \Rightarrow f\left( x \right) < 0\,\,\forall x \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2 < 0\,\,\forall m\\{m^2} + 12m - 28 < 0\end{array} \right.\\ \Leftrightarrow \left( {m - 2} \right)\left( {m + 14} \right) < 0 \Leftrightarrow - 14 < m < 2.\end{array}\) Vậy với \(m \in \left( { - 14;2} \right)\) thỏa mãn yêu cầu đề bài. Chọn C. Câu hỏi 14 : Tìm tất cả các giá trị thực của tham số m để hàm số \(y = \sqrt {x - m} - \sqrt {6 - 2x} \) có tập xác định là một đoạn trên trục số.
Đáp án: B Phương pháp giải: \(\sqrt A \) xác định \( \Leftrightarrow A \ge 0\). Lời giải chi tiết: ĐKXĐ: \(\left\{ \begin{array}{l}x - m \ge 0\\6 - 2x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge m\\x \le 3\end{array} \right. \Leftrightarrow m \le x \le 3\). Để hàm số có TXĐ là một đoạn trên trục số thì \(m < 3\). Chọn B. Câu hỏi 15 : Phương trình \({x^2} + x + m = 0\) vô nghiệm khi và chỉ khi:
Đáp án: C Phương pháp giải: Phương trình bậc hai vô nghiệm \( \Leftrightarrow \Delta < 0\). Lời giải chi tiết: Phương trình vô nghiệm \( \Leftrightarrow \Delta < 0 \Leftrightarrow 1 - 4m < 0 \Leftrightarrow m > \dfrac{1}{4}\). Chọn C. Câu hỏi 16 : Điều kiện xác định của bất phương trình \(2018\sqrt {x + 2} > 2019{x^2} + \frac{1}{{x - 2}}\) là:
Đáp án: C Phương pháp giải: \(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0\) \(\frac{1}{{g\left( x \right)}}\) xác định \( \Leftrightarrow g\left( x \right) \ne 0\) Lời giải chi tiết: \(2018\sqrt {x + 2} > 2019{x^2} + \frac{1}{{x - 2}}\) ĐKXĐ: \(\left\{ \begin{array}{l}x + 2 \ge 0\\x - 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\x \ne 2\end{array} \right.\) Chọn C. Câu hỏi 17 : Nhị thức \(f\left( x \right) = 3x + 2\) nhận giá trị âm khi:
Đáp án: B Phương pháp giải: Xét dấu của nhị thức theo quy tắc: Phải cùng trái khác hay Lớn cùng bé khác. Lời giải chi tiết: Nhị thức \(f\left( x \right) = 3x + 2\) nhận giá trị âm khi \(x < - \frac{2}{3}\) Chọn B. Câu hỏi 18 : Có bao nhiêu giá trị của tham số \(m\) để hệ bất phương trình \(\left\{ \begin{array}{l}x - 3 \ge m\\\left( {m - 2} \right)x \le 3m - 3\end{array} \right.\) có nghiệm duy nhất ?
Đáp án: B Phương pháp giải: Biến đổi hệ BPT và biện luận. Lời giải chi tiết: +) Với \(m = 2\) HPT trở thành : \(\left\{ \begin{array}{l}x - 3 \ge 2\\0 \le 3\end{array} \right. \Leftrightarrow x \ge 5\) không có nghiệm duy nhất. +) Với \(m > 2\) ta có : \(\left\{ \begin{array}{l}x - 3 \ge m\\\left( {m - 2} \right)x \le 3m - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge m + 3\\x \le \frac{{3m - 3}}{{m - 2}}\end{array} \right.\) HPT có nghiệm duy nhất \( \Leftrightarrow m + 3 = \frac{{3m - 3}}{{m - 2}} \Leftrightarrow {m^2} + m - 6 = 3m - 3 \Leftrightarrow {m^2} - 2m - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 3\,\,\,\left( {tm} \right)\\m = - 1\,\,\,\left( {ktm} \right)\end{array} \right.\) +) Với \(m < 2\) ta có : \(\left\{ \begin{array}{l}x - 3 \ge m\\\left( {m - 2} \right)x \le 3m - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge m + 3\\x \ge \frac{{3m - 3}}{{m - 2}}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge m + 3\\x \ge \frac{{3m - 3}}{{m - 2}}\end{array} \right.\) \( \Rightarrow \) HPT không có nghiệm duy nhất. Vậy có 1 giá trị của \(m\) thỏa mãn yêu cầu đề bài. Chọn B. Câu hỏi 19 : Tập nghiệm của bất phương trình \(\frac{2}{x} > - 1\) là:
Đáp án: C Phương pháp giải: Giải BPT có chứa ẩn ở mẫu. Lời giải chi tiết: ĐKXĐ: \(x \ne 0\) \(\frac{2}{x} > - 1 \Leftrightarrow \frac{2}{x} + 1 > 0 \Leftrightarrow \frac{{2 + x}}{x} > 0 \Leftrightarrow \left[ \begin{array}{l}x < - 2\\x > 0\end{array} \right.\) Kết hợp với ĐKXĐ ta được tập nghiệm của BPT là \(\left( { - \infty ; - 2} \right) \cup \left( {0; + \infty } \right).\) Chọn C. Câu hỏi 20 : Phương trình \({x^2} - 2\left( {m - 1} \right)x + m - 3 = 0\) có hai nghiệm đối nhau khi và chỉ khi:
Đáp án: C Phương pháp giải: Phương trình bậc hai có 2 nghiệm đối nhau khi và chỉ khi phương trình có 2 nghiệm phân biệt thỏa mãn \(S = 0\). Lời giải chi tiết: Phương trình \({x^2} - 2\left( {m - 1} \right)x + m - 3 = 0\) có hai nghiệm đối nhau \( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\S = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {m - 1} \right)^2} - m + 3 > 0\\m - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 3m + 4 > 0\\m = 1\end{array} \right. \Leftrightarrow m = 1\). Chọn C. Câu hỏi 21 : Hệ bất phương trình \(\left\{ \begin{array}{l}{x^2} - 4x + 3 \ge 0\\3{x^2} - 10x + 3 \le 0\\4{x^2} - x - 3 > 0\end{array} \right.\) có nghiệm là:
Đáp án: A Phương pháp giải: Lập bảng xét dấu và kết luận nghiệm. Lời giải chi tiết: Giải các phương trình: \(\begin{array}{l}{x^2} - 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\\3{x^2} - 10x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = \dfrac{1}{3}\end{array} \right.\\4{x^2} - x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - \dfrac{3}{4}\end{array} \right.\end{array}\) Bảng xét dấu:
Từ BXD ta có: \(\left\{ \begin{array}{l}{x^2} - 4x + 3 \ge 0\\3{x^2} - 10x + 3 \le 0\\4{x^2} - x - 3 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \in \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)\\x \in \left[ {\dfrac{1}{3};3} \right]\\x \in \left( { - \infty ; - \dfrac{3}{4}} \right) \cup \left( {1; + \infty } \right)\end{array} \right. \Leftrightarrow x = 3\). Chọn A. Câu hỏi 22 : Nghiệm của bất phương trình \(\left( {{x^2} + x - 2} \right)\sqrt {2{x^2} - 1} < 0\) là:
Đáp án: C Phương pháp giải: \(AB < 0 \Leftrightarrow A,\,\,B\) trái dấu. Lời giải chi tiết: ĐKXĐ: \(2{x^2} - 1 \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le - \dfrac{1}{{\sqrt 2 }}\\x \ge \dfrac{1}{{\sqrt 2 }}\end{array} \right.\). \(\left( {{x^2} + x - 2} \right)\sqrt {2{x^2} - 1} < 0 \Leftrightarrow \left\{ \begin{array}{l}{x^2} + x - 2 < 0\\2{x^2} - 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2 < x < 1\\x \ne \pm \dfrac{1}{{\sqrt 2 }}\end{array} \right.\). Kết hợp ĐK \( \Rightarrow x \in \left( { - 2;\dfrac{{ - 1}}{{\sqrt 2 }}} \right) \cup \left( {\dfrac{1}{{\sqrt 2 }};1} \right)\). Chọn C. Câu hỏi 23 : Tìm tất cả các giá trị của \(a\) để bất phương trình \(a{x^2} - x + a \ge 0\,\,\forall x \in \mathbb{R}\).
Đáp án: D Phương pháp giải: \(a{x^2} + bx + c \ge 0\,\,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta \le 0\end{array} \right.\). Lời giải chi tiết: \(a{x^2} - x + a \ge 0\,\,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta = 1 - 4{a^2} \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\left[ \begin{array}{l}a \le - \dfrac{1}{2}\\a \ge \dfrac{1}{2}\end{array} \right.\end{array} \right. \Leftrightarrow a \ge \dfrac{1}{2}\). Chọn D. Câu hỏi 24 : Cho hệ bất phương trình \(\left\{ \begin{array}{l}x + 2y - 3 < 0\\2x + y - 2 > 0\end{array} \right.\). Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho?
Đáp án: D Phương pháp giải: Thay tọa độ từng điểm vào hệ BPT để kiểm chứng. Lời giải chi tiết: Ta có: \(\left\{ \begin{array}{l}3 + 2.\left( { - 1} \right) - 3 = - 2 < 0\\2.3 + \left( { - 1} \right) - 2 = 3 > 0\end{array} \right.\) Vậy \(P\left( {3; - 1} \right)\) thuộc miền nghiệm của hệ BPT đã cho. Chọn D. Câu hỏi 25 : Tìm nghiệm nguyên dương của bất phương trình: \(\frac{{5\left( {x - 1} \right)}}{6} - 1 < \frac{{2\left( {x + 1} \right)}}{3}\)
Đáp án: C Phương pháp giải: Quy đồng, bỏ mẫu và giải bất phương trình. Lời giải chi tiết: \(\begin{array}{l}\frac{{5\left( {x - 1} \right)}}{6} - 1 < \frac{{2\left( {x + 1} \right)}}{3}\\ \Leftrightarrow 5x - 5 - 6 < 4x + 4\\ \Leftrightarrow x < 15\end{array}\) Vậy tập nghiệm nguyên dương của bất phương trình là: \(S{\rm{ }} = \left\{ {1;\,\,2;\,\,3;\,\,4; \ldots ;\,\,14} \right\}.\) Câu hỏi 26 : Bất phương trình \(\left| {3x + 2} \right| > 4\) có nghiệm là:
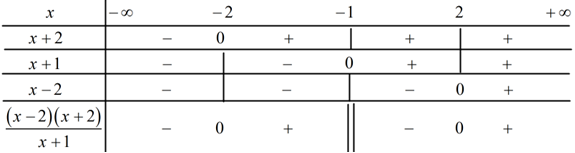
Đáp án: D Phương pháp giải: Giải bất phương trình chứa dấu giá trị tuyệt đối: \(\left| A \right| > a\,\,\,\left( {a > 0} \right) \Leftrightarrow \left[ \begin{array}{l}A > a\\A < - a\end{array} \right..\) Lời giải chi tiết: \(\left| {3x + 2} \right| > 4 \Leftrightarrow \left[ \begin{array}{l}3x + 2 > 4\\3x + 2 < - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}3x > 2\\3x < - 6\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > \frac{2}{3}\\x < - 2\end{array} \right.\) Chọn D. Câu hỏi 27 : Giải bất phương trình sau: \(\frac{{{x^2} - 4}}{{x + 1}} \ge 0\)
Đáp án: B Phương pháp giải: Tìm điều kiện để biểu thức có nghĩa sau đó lập bảng xét dấu. Lời giải chi tiết: Điều kiện: \(x + 1 \ne 0 \Leftrightarrow x \ne - 1.\) \(\frac{{{x^2} - 4}}{{x + 1}} \ge 0 \Leftrightarrow \frac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{x + 1}} \ge 0\) Xét \(\left( {x - 2} \right)\left( {x + 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\) Ta có bảng xét dấu: Vậy \(\frac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{x + 1}} \ge 0 \Leftrightarrow \,\left[ \begin{array}{l} - 2 \le x < - 1\\x \ge 2\end{array} \right..\) Chọn B. Câu hỏi 28 : Tập nghiệm của bất phương trình: \(\left| {{x}^{2}}-4 \right|\le 2x+11\)là:
Đáp án: A Phương pháp giải: Sử dụng phép biến đổi tương đương: Với \(a>0\) thì \(|x|\le a\Leftrightarrow -a\le x\le a\) Lời giải chi tiết: Điều kiện \(2x+11\ge 0\Leftrightarrow x\ge -\frac{11}{2}\) Khi đó, ta có: \(\begin{array}{l}\left| {{x^2} - 4} \right| \le 2x + 11 \Leftrightarrow - 2x - 11 \le {x^2} - 4 \le 2x + 11\\ \Leftrightarrow \left\{ \begin{array}{l} - {x^2} - 2x - 7 \le 0\\{x^2} - 2x - 15 \le 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - {\left( {x + 1} \right)^2} - 6 \le 0\\\left( {x + 3} \right)\left( {x - 5} \right) \le 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\forall x \in R\\ - 3 \le x \le 5\end{array} \right. \Leftrightarrow - 3 \le x \le 5\end{array}\) Chọn A. Câu hỏi 29 : Tập nghiệm của bất phương trình \(|{{x}^{2}}+x-3|>{{x}^{2}}+3x+3\) là:
Đáp án: D Phương pháp giải: Sử dụng phép biến đổi tương đương: Với \(a>0\) thì \(|x| \ge a \Leftrightarrow \left[ \begin{array}{l}x \ge a\\x \le - a\end{array} \right.\) Lời giải chi tiết: Nhận xét \({{x}^{2}}+3x+3={{\left( x+\frac{3}{2} \right)}^{2}}+\frac{3}{4}>0\) nên ta có: \(\begin{array}{l}|{x^2} + x - 3| > {x^2} + 3x + 3\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} + x - 3 > {x^2} + 3x + 3\\{x^2} + x - 3 < - {x^2} - 3x - 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} - 2x - 6 > 0\\2{x^2} + 4x < 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x + 3 < 0\\2x(x + 2) < 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x < - 3\\ - 2 < x < 0\end{array} \right.\end{array}\) Vậy nghiệm của bất phương trình là \(S=\left( -\infty ;-3 \right)\bigcup \left( -2;0 \right)\) Chọn D. Câu hỏi 30 : Bất phương trình \(\sqrt{{{x}^{2}}-x-12}<x\) có tất cả bao nhiêu nghiệm nguyên trên \(\left[ -\,2018;2018 \right]\) ?
Đáp án: C Phương pháp giải: Áp dụng phương pháp giải bất phương trình chứa căn thức dạng \(\sqrt{f\left( x \right)}<g\left( x \right)\Leftrightarrow \left\{ \begin{align} g\left( x \right)>0 \\ f\left( x \right)\ge 0 \\ f\left( x \right)<{{g}^{2}}\left( x \right) \\ \end{align} \right.\) Lời giải chi tiết: Bất phương trình \(\sqrt {{x^2} - x - 12} < x \Leftrightarrow \left\{ \begin{array}{l}x > 0\\{x^2} - x - 12 \ge 0\\{x^2} - x - 12 < {x^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 0\\\left[ \begin{array}{l}x \ge 4\\x \le - 3\end{array} \right.\\x > - 12\end{array} \right. \Leftrightarrow x \ge 4.\) Kết hợp với điều kiện \(x\in Z\) và \(x\in \left[ -\,2018;2018 \right]\Rightarrow x\in \left[ 4;2018 \right]\)\(\Rightarrow \) có 2015 nghiệm nguyên thỏa mãn. Chọn C Câu hỏi 31 : Cho tam thức \(f(x) = a{x^2} + bx + c,{\rm{(a}} \ne {\rm{0),}}\,\,\Delta {\rm{ = }}{{\rm{b}}^2} - 4ac\). Ta có \(f(x) \le 0\) với \(\forall x \in R\) khi và chỉ khi:
Đáp án: A Phương pháp giải: Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) có biệt thức \(\Delta = {b^2} - 4ac\) - Nếu \(\Delta < 0\) thì với mọi \(x,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta = 0\) thì \(f\left( x \right)\) có nghiệm kép \(x = - \frac{b}{{2a}}\), với mọi \(x \ne - \frac{b}{{2a}},\,\,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta > 0\),\(f\left( x \right)\)có 2 nghiệm \({x_1},{x_2}\,\,\left( {{x_1} < {x_2}} \right)\) và luôn cùng dấu với hệ số a với mọi x ngoài khoảng \(\left( {{x_1};\;{x_2}} \right)\) và luôn trái dấu với hệ số a với mọi x trong khoảng \(\left( {{x_1};\;{x_2}} \right).\) Lời giải chi tiết: Cho tam thức \(f(x) = a{x^2} + bx + c\;\;\;\left( {a \ne 0} \right){\rm{,}}\,\,\Delta = {b^2} - 4ac\) \(f(x) \le 0\) với \(\forall x \in R\) \( \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta \le 0\end{array} \right.\) Chọn A. Câu hỏi 32 : Cho \(f(x) = - {x^2} + 3x - 2;f(x) \ge 0\). Nghiệm của bất phương trình là?
Đáp án: A Phương pháp giải: Sử dụng quy tắc trong trái ngoài cùng. Lời giải chi tiết: Với \(f(x) = - {x^2} + 3x - 2;\)ta có: \(a = 1;\,\,\Delta = 1;\,\,f\left( x \right) = 0\) có hai nghiệm \({x_1} = 1;\,\,{x_2} = 2\). Bảng xét dấu
Chọn A. Câu hỏi 33 : Cho hàm số \(f\left( x \right) = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\). Biết rằng \(a < 0\,\,;\,\,\Delta = {b^2} - 4ac < 0\). Mệnh đề nào sau đây đúng ?
Đáp án: D Phương pháp giải: Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) có biệt thức \(\Delta = {b^2} - 4ac\) - Nếu \(\Delta < 0\) thì với mọi \(x,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta = 0\) thì \(f\left( x \right)\) có nghiệm kép \(x = - \frac{b}{{2a}}\), với mọi \(x \ne - \frac{b}{{2a}},\,\,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta > 0\),\(f\left( x \right)\)có 2 nghiệm \({x_1},{x_2}\,\,\left( {{x_1} < {x_2}} \right)\) và luôn cùng dấu với hệ số a với mọi x ngoài khoảng \(\left( {{x_1};\,\,{x_2}} \right)\) và luôn trái dấu với hệ số a với mọi x trong khoảng \(\left( {{x_1};\,\,{x_2}} \right).\) Lời giải chi tiết: Cho hàm số \(f\left( x \right) = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\). Biết rằng \(a < 0\,\,;\,\,\Delta = {b^2} - 4ac < 0\) \( \Rightarrow f\left( x \right) < 0,\,\,\forall x \in \mathbb{R}\) Chọn D. Câu hỏi 34 : Tập nghiệm của bất phương trình \(\left| \frac{{{x}^{2}}-4}{{{x}^{2}}+x+2} \right|\le 1\) là:
Đáp án: C Phương pháp giải: Sử dụng phép biến đổi tương đương: Với \(a>0\) thì \(|x|\le a\Leftrightarrow -a\le x\le a\) Lời giải chi tiết: \(\left| {\frac{{{x^2} - 4}}{{{x^2} + x + 2}}} \right| \le 1 \Leftrightarrow - 1 \le \frac{{{x^2} - 4}}{{{x^2} + x + 2}} \le 1 \Leftrightarrow \left\{ \begin{array}{l}\frac{{{x^2} - 4}}{{{x^2} + x + 2}} \le 1\\\frac{{{x^2} - 4}}{{{x^2} + x + 2}} \ge - 1\end{array} \right.\) (*) Vì \({{x}^{2}}+x+2={{\left( x+\frac{1}{2} \right)}^{2}}+\frac{7}{4}>0\) nên ta có \((*) \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 4 \le {x^2} + x + 2\\{x^2} - 4 \ge - \left( {{x^2} + x + 2} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - x - 6 \le 0\\2{x^2} + x - 2 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 6\\\left[ \begin{array}{l}x \ge \frac{{ - 1 + \sqrt {17} }}{4}\\x \le \frac{{ - 1 - \sqrt {17} }}{4}\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge \frac{{ - 1 + \sqrt {17} }}{4}\\ - 6 \le x \le \frac{{ - 1 - \sqrt {17} }}{4}\end{array} \right.\) Vậy nghiệm của bất phương trình là: \(S=\left[ -6;\frac{-1-\sqrt{17}}{4} \right]\cup \left[ \frac{-1+\sqrt{17}}{4};+\infty \right)\) Chọn C. Câu hỏi 35 : Tập nghiệm của bất phương trình \(\left| \frac{{{x}^{2}}+3x+2}{{{x}^{2}}-3x+2} \right|\ge 1\) là:
Đáp án: C Phương pháp giải: Sử dụng phép biến đổi tương đương: Với \(a>0\) thì \(|x| \ge a \Leftrightarrow \left[ \begin{array}{l}x \ge a\\x \le - a\end{array} \right.\) Lời giải chi tiết: \(\begin{array}{l}\left| {\frac{{{x^2} + 3x + 2}}{{{x^2} - 3x + 2}}} \right| \ge 1 \Leftrightarrow \left[ \begin{array}{l}\frac{{{x^2} + 3x + 2}}{{{x^2} - 3x + 2}} \ge 1\\\frac{{{x^2} + 3x + 2}}{{{x^2} - 3x + 2}} \le - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\frac{{{x^2} + 3x + 2}}{{{x^2} - 3x + 2}} - 1 \ge 0\\\frac{{{x^2} + 3x + 2}}{{{x^2} - 3x + 2}} + 1 \le 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\frac{{{x^2} + 3x + 2 - \left( {{x^2} - 3x + 2} \right)}}{{{x^2} - 3x + 2}} \ge 0\\\frac{{{x^2} + 3x + 2 + \left( {{x^2} - 3x + 2} \right)}}{{{x^2} - 3x + 2}} \le 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\frac{{6x}}{{{x^2} - 3x + 2}} \ge 0\\\frac{{2{x^2} + 4}}{{{x^2} - 3x + 2}} \le 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\frac{{6x}}{{\left( {x - 1} \right)\left( {x - 2} \right)}} \ge 0\\\frac{{2{x^2} + 4}}{{\left( {x - 1} \right)\left( {x - 2} \right)}} \le 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\frac{{6x}}{{\left( {x - 1} \right)\left( {x - 2} \right)}} \ge 0\\\left( {x - 1} \right)\left( {x - 2} \right) < 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 2\\0 \le x < 1\\1 < x < 2\end{array} \right.\end{array}\) Vậy nghiệm của bất phương trình là \(S=\left[ 0;+\infty \right)\backslash \left\{ 1;2 \right\}\) Chọn C. Câu hỏi 36 : Tìm giá trị của m để \(f(x) = \left( {m + 1} \right){x^2} - 2(m - 1)x + 3m - 3 \ge 0{\rm{ }}\forall x\)
Đáp án: D Phương pháp giải: \(a{x^2} + bx + c \ge 0\,\,\forall x \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta \le 0\end{array} \right.\) Lời giải chi tiết: Với \(m+1=0\Leftrightarrow m=-1\Rightarrow f(x)=4x-6\) do đó không thể có \(f(x)\ge 0\text{ }\forall x\) Với \(m+1\ne 0\Leftrightarrow m\ne -1\) . Khi đó: \(\begin{array}{l} Chọn D. Câu hỏi 37 : Tập nghiệm của bất phương trình \(\left| {{x}^{2}}+3x+2 \right|+{{x}^{2}}+2x\ge 0\) là:
Đáp án: D Phương pháp giải: Phá dấu giá trị tuyệt đối. \(\left| {{x^2} + 3x + 2} \right| = \left\{ \begin{array}{l}{x^2} + 3x + 2\,\,\,\,\,\,khi\,\,\left[ \begin{array}{l}x \ge - 1\\x \le - 2\end{array} \right.\,\\ - {x^2} - 3x - 2\,\,\,khi\,\, - 2 < x < - 1\end{array} \right.\) Do đó, ta xét 2 trường hợp TH1: \(\left[ \begin{array}{l}x \ge - 1\\x \le - 2\end{array} \right.\) TH2: \(-2<x<-1\) Lời giải chi tiết:
Ta xét 2 trường hợp TH1: \(\left[ \begin{array}{l}x \ge - 1\\x \le - 2\end{array} \right.\) \(\left| {{x^2} + 3x + 2} \right| + {x^2} + 2x \ge 0 \Leftrightarrow {x^2} + 3x + 2 + {x^2} + 2x \ge 0 \Leftrightarrow 2{x^2} + 5x + 2 \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \ge - \frac{1}{2}\\x \le - 2\end{array} \right.\) Kết hợp với điều kiện \(\left[ \begin{array}{l}x \ge - 1\\x \le - 2\end{array} \right.\) ta có \(\left[ \begin{array}{l}x \ge - \frac{1}{2}\\x \le - 2\end{array} \right.\) TH2: \(-2<x<-1\) \(\left| {{x}^{2}}+3x+2 \right|+{{x}^{2}}+2x\ge 0\Leftrightarrow -{{x}^{2}}-3x-2+{{x}^{2}}+2x\ge 0\Leftrightarrow -x-2\ge 0\Leftrightarrow x\le -2\) Kết hợp với điều kiện \(-2<x<-1\) ta loại nghiệm \(x\le -2\). Vậy tập nghiệm của bất phương trình là \(S=\left( -\infty ;-2 \right]\cup \left[ -\frac{1}{2};+\infty \right)\) Chọn D Câu hỏi 38 : Tập nghiệm của bất phương trình \(\left| {{x}^{2}}-x \right|\le \left| {{x}^{2}}-1 \right|\) là:
Đáp án: B Phương pháp giải: Sử dụng phương pháp biến đổi \(\left| a \right|\le \left| b \right|\Leftrightarrow {{a}^{2}}\le {{b}^{2}}\) Lời giải chi tiết: \(\left| {{x}^{2}}-x \right|\le \left| {{x}^{2}}-1 \right|\Leftrightarrow \left| x\left( x-1 \right) \right|\le \left| \left( x-1 \right)\left( x+1 \right) \right|\Leftrightarrow \left| x \right|\left| x-1 \right|\le \left| x-1 \right|\left| x+1 \right|\) Ta thấy \(x=1\)là nghiệm của bất phương trình Với \(x\ne 1\), ta có\(\begin{array}{l}\left| x \right|\left| {x - 1} \right| \le \left| {x - 1} \right|\left| {x + 1} \right| \Leftrightarrow \left| x \right| \le \left| {x + 1} \right|\\ \Leftrightarrow {x^2} \le {\left( {x + 1} \right)^2} \Leftrightarrow {x^2} - {\left( {x + 1} \right)^2} \le 0 \Leftrightarrow \left( {x - x - 1} \right)\left( {x + x + 1} \right) \le 0\\ \Leftrightarrow \left( { - 1} \right).\left( {2x + 1} \right) \le 0 \Leftrightarrow 2x + 1 \ge 0 \Leftrightarrow x \ge - \frac{1}{2}\end{array}\) Kết hợp hai trường hợp ta có nghiệm của bất phương trình là \(S=\left[ -\frac{1}{2};+\infty \right)\) Chọn B. Câu hỏi 39 : Tập xác định của hàm số \(y = \sqrt {{x^2} + 4x - 5} \) là:
Đáp án: C Phương pháp giải: \(\sqrt A \) xác định \( \Leftrightarrow A \ge 0\) Lời giải chi tiết: Điều kiện xác định của hàm số \(y = \sqrt {{x^2} + 4x - 5} : {x^2} + 4x - 5 \ge 0 \Leftrightarrow \left[ \matrix{ x \ge 1 \hfill \cr x \le - 5 \hfill \cr} \right.\) Tập xác định của hàm số \(y = \sqrt {{x^2} + 4x - 5} \) là \(D = \left( { - \infty ; - 5} \right] \cup \left[ {1; + \infty } \right)\). Chọn: C Câu hỏi 40 : Tập nghiệm của bất phương trình \(2{{x}^{2}}+4x+3\sqrt{3-2x-{{x}^{2}}}>1\) có dạng \(S=\left[ a;b \right].\) Tính \(a-b.\)
Đáp án: C Phương pháp giải: Đặt ẩn phụ bằng căn, đưa về các dạng bất phương trình cơ bản Lời giải chi tiết: Điều kiện: \(3-2x-{{x}^{2}}\ge 0\Leftrightarrow x\in \left[ -\,3;1 \right].\) Đặt \(t=\sqrt{3-2x-{{x}^{2}}}\ge 0\Leftrightarrow {{x}^{2}}+2x=3-{{t}^{2}}.\) Khi đó, bất phương trình đã cho trở thành: \(2\left( 3-{{t}^{2}} \right)+3t>1\Leftrightarrow 2{{t}^{2}}-3t-5<0\Leftrightarrow -\,1<t<\frac{5}{2}.\) Kết hợp điều kiện: \(t\ge 0,\) ta được \(0\le t<\frac{5}{2}\Leftrightarrow \sqrt{3-2x-{{x}^{2}}}<\frac{5}{2}\Leftrightarrow \left\{ \begin{align} -\,3\le x\le 1 \\ 4\left( 3-2x-{{x}^{2}} \right)<25 \\ \end{align} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l} - 3 \le x \le 1\\4{x^2} + 8x + 13 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 3 \le x \le 1\\4{\left( {x + 1} \right)^2} + 9 > 0\end{array} \right. \Leftrightarrow - 3 \le x \le 1.\) Vậy \(S=\left[ -\,3;1 \right]=\left[ a;b \right]\Rightarrow a-b=-\,4.\) Chọn C Câu hỏi 41 : Tập nghiệm của bất phương trình \(\sqrt{-\,{{x}^{2}}+6x-5}>8-2x\) có dạng \(\left( a;b \right].\) Tính \({{a}^{2}}-2b.\)
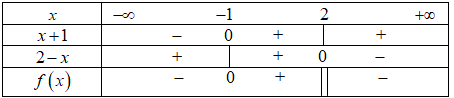
Đáp án: B Phương pháp giải: Áp dụng phương pháp giải bất phương trình chứa căn thức dạng \(\sqrt {f\left( x \right)} > g\left( x \right) \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}f\left( x \right) \ge 0\\g\left( x \right) \le 0\end{array} \right.\\\left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) > {g^2}\left( x \right)\end{array} \right.\end{array} \right.\) Lời giải chi tiết: Bất phương trình \(\sqrt { - {x^2} + 6x - 5} > 8 - 2x \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l} - {x^2} + 6x - 5 \ge 0\\8 - 2x \le 0\end{array} \right.\left( 1 \right)\\\left\{ \begin{array}{l}8 - 2x > 0\\ - {x^2} + 6x - 5 > {\left( {8 - 2x} \right)^2}\end{array} \right.\left( 2 \right)\end{array} \right..\) Giải ta có \(\left( 1 \right) \Leftrightarrow \left\{ \begin{array}{l} - {x^2} + 6x - 5 \ge 0\\8 - 2x \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 6x + 5 \le 0\\x \ge 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 \le x \le 5\\x \ge 4\end{array} \right. \Leftrightarrow 4 \le x \le 5.\) Giải ta có \(\left( 2 \right) \Leftrightarrow \left\{ \begin{array}{l}x < 4\\ - {x^2} + 6x - 5 > 4{x^2} - 32x + 64\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < 4\\5{x^2} - 38x + 69 < 0\end{array} \right. \Leftrightarrow 3 < x < 4.\) Kết hợp với hai TH, ta được tập nghiệm của bất phương trình là \(S=\left( 3;5 \right]=\left( a;b \right]\Rightarrow \left\{ \begin{align} a=3 \\ b=5 \\ \end{align} \right..\) Chọn B Câu hỏi 42 : Cho bảng xét dấu: Hàm số có bảng xét dấu như trên là
Đáp án: A Phương pháp giải: Dựa vào bảng xét dấu để tìm từng hệ số a, b của hàm số \(f\left( x \right) = ax + b\) Xét phương trình:\(f\left( x \right) = 0 \Leftrightarrow ax + b = 0\) có nghiệm \(x = {x_0}\) thì: +) Số \({x_1} > {x_0}\) thì \(f\left( {{x_1}} \right)\) cùng dấu với \(a.\) +) Số \({x_1} < {x_0}\) thì \(f\left( {{x_1}} \right)\) trái dấu với \(a.\) Lời giải chi tiết: Gọi hàm số cần tìm có dạng \(f\left( x \right) = ax + b\) Nhìn bảng xét dấu ta thấy với \({x_1} > - 2\) thì \(f\left( {{x_1}} \right) < 0 \Rightarrow \) hệ số \(a < 0\) \( \Rightarrow \) Loại B, D Mặt khác với \(x = - 2\) thì \(f\left( x \right) = 0 \Rightarrow \) Chọn A. Chọn A. Câu hỏi 43 : Cho tam thức bậc hai \(f(x) = - 2{x^2} + 8x - 8\). Trong các mệnh đề sau, mệnh đề nào đúng?
Đáp án: C Phương pháp giải: Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) có biệt thức \(\Delta = {b^2} - 4ac\) - Nếu \(\Delta < 0\) thì với mọi \(x,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta = 0\)thì \(f\left( x \right)\) có nghiệm kép \(x = - \frac{b}{{2a}}\), với mọi \(x \ne - \frac{b}{{2a}},\,\,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta > 0\),\(f\left( x \right)\)có 2 nghiệm \({x_1},{x_2}\,\,\left( {{x_1} < {x_2}} \right)\) và luôn cùng dấu với hệ số a với mọi x ngoài khoảng \(\left( {{x_1};\;{x_2}} \right)\) và luôn trái dấu với hệ số a với mọi x trong khoảng \(\left( {{x_1};\;{x_2}} \right).\) Lời giải chi tiết: Ta có : \(\left\{ \begin{array}{l}a = - 2 < 0\\\Delta ' = 16 - 16 = 0\end{array} \right.\) \( \Rightarrow f(x) \le 0\) với mọi \(x \in R\) Chọn C. Câu hỏi 44 : Tam thức \(f\left( x \right) = - {x^2} - 2x + 3\) nhận giá trị dương khi và chỉ khi:
Đáp án: C Phương pháp giải: Xét dấu của nhị thức theo quy tắc: Trong trái ngoài cùng. Lời giải chi tiết: \(\begin{array}{l}f\left( x \right) = - {x^2} - 2x + 3 > 0 \Leftrightarrow {x^2} + 2x - 3 < 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x + 3} \right) < 0 \Leftrightarrow - 3 < x < 1.\end{array}\) Chọn C. Câu hỏi 45 : Tìm giá trị của m để \(f(x) = \left( {m + 1} \right){x^2} - 2(m - 1)x + 3m - 3 < 0{\rm{ }}\forall x\) .
Đáp án: B Phương pháp giải: \(a{x^2} + bx + c < 0\,\,\forall x \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta < 0\end{array} \right.\) Lời giải chi tiết: Với \(m + 1 = 0 \Leftrightarrow m = - 1 \Rightarrow f(x) = 4x - 6\) do đó không thể có \(f(x) < 0{\rm{ }}\forall x\) Với \(m + 1 \ne 0 \Leftrightarrow m \ne - 1\) . Khi đó: \(\begin{array}{l} Chọn B. Câu hỏi 46 : Tập nghiệm của bất phương trình: \(\left| {{x}^{2}}-5x-2 \right|\ge 3x-1\) là:
Đáp án: A Phương pháp giải: Sử dụng phép biến đổi tương đương: Với \(a\ge 0\) thì \(|x| \ge a \Leftrightarrow \left[ \begin{array}{l}x \ge a\\x \le - a\end{array} \right.\) Lời giải chi tiết: +) \(TH1:\,3x-1<0\Leftrightarrow x<\frac{1}{3}\) , bất phương trình luôn đúng. +) TH2:\(3x-1\ge 0\Leftrightarrow x\ge \frac{1}{3}\). Ta có \(\begin{array}{l}\left| {{x^2} - 5x - 2} \right| \ge 3x - 1\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} - 5x - 2 \ge 3x - 1\\{x^2} - 5x - 2 \le - 3x + 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} - 8x - 1 \ge 0\\{x^2} - 2x - 3 \le 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x \ge 4 + \sqrt {17} \\x \le 4 - \sqrt {17} \\ - 1 \le x \le 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x \ge 4 + \sqrt {17} \\x \le 3\end{array} \right.\end{array}\) Kết hợp điều kiện: \(x\ge \frac{1}{3}\) ta có nghiệm trong TH2 là: \(\left[ \begin{array}{l}x \ge 4 + \sqrt {17} \\\frac{1}{3} \le x \le 3\end{array} \right.\) Kết hợp hai trường hợp ta có nghiệm của bất phương trình là:\(S=\left( -\infty ;3 \right]\cup \left[ 4+\sqrt{17};+\infty \right).\) Chọn A Câu hỏi 47 : Tam thức bậc hai nào sau đây luôn dương với mọi \(x \in \mathbb{R}\)?
Đáp án: C Phương pháp giải: Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) có biệt thức \(\Delta = {b^2} - 4ac\) - Nếu \(\Delta < 0\) thì với mọi \(x,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta = 0\)thì \(f\left( x \right)\) có nghiệm kép \(x = - \frac{b}{{2a}}\), với mọi \(x \ne - \frac{b}{{2a}},\,\,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta > 0\),\(f\left( x \right)\)có 2 nghiệm \({x_1},{x_2}\,\,\left( {{x_1} < {x_2}} \right)\) và luôn cùng dấu với hệ số a với mọi x ngoài khoảng \(\left( {{x_1};\,\,{x_2}} \right)\) và luôn trái dấu với hệ số a với mọi x trong khoảng \(\left( {{x_1};\,\,{x_2}} \right).\) Lời giải chi tiết: Tam thức: \({x^2} + x + 1\) có \(\Delta = 1 - 4 = - 3 < 0\) Vậy tam thức bậc hai \({x^2} + x + 1\) luôn dương với mọi \(x \in \mathbb{R}\) Chọn C. Câu hỏi 48 : Cho hàm số \(f\left( x \right) = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\). Biết rằng \(a < 0\,\,;\,\,\Delta = {b^2} - 4ac < 0\). Mệnh đề nào sau đây đúng ?
Đáp án: D Phương pháp giải: Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) có biệt thức \(\Delta = {b^2} - 4ac\) - Nếu \(\Delta < 0\) thì với mọi \(x,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta = 0\) thì \(f\left( x \right)\) có nghiệm kép \(x = - \frac{b}{{2a}}\), với mọi \(x \ne - \frac{b}{{2a}},\,\,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta > 0\),\(f\left( x \right)\)có 2 nghiệm \({x_1},{x_2}\,\,\left( {{x_1} < {x_2}} \right)\) và luôn cùng dấu với hệ số a với mọi x ngoài khoảng \(\left( {{x_1};\,\,{x_2}} \right)\) và luôn trái dấu với hệ số a với mọi x trong khoảng \(\left( {{x_1};\,\,{x_2}} \right).\) Lời giải chi tiết: Cho hàm số \(f\left( x \right) = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\). Biết rằng \(a < 0\,\,;\,\,\Delta = {b^2} - 4ac < 0\) \( \Rightarrow f\left( x \right) < 0,\,\,\forall x \in \mathbb{R}\) Chọn D. Câu hỏi 49 : Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\,\,\,\left( {a \ne 0} \right).\) Điều kiện cần và đủ để \(f\left( x \right) < 0\,\,\forall \,x \in \mathbb{R}\) là:
Đáp án: D Phương pháp giải: Cho tam thức bậc hai:\(f\left( x \right) = a{x^2} + bx + c\,\,\,\left( {a \ne 0} \right).\) Khi đó \(f\left( x \right) < 0\,\,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta < 0\end{array} \right..\) Lời giải chi tiết: Cho tam thức bậc hai:\(f\left( x \right) = a{x^2} + bx + c\,\,\,\left( {a \ne 0} \right).\) Khi đó \(f\left( x \right) > 0\,\,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta < 0\end{array} \right..\) Chọn D. Câu hỏi 50 : Cho tam thức \(f\left( x \right) = {x^2} - 8x + 16\). Khẳng định nào sau đây là đúng?
Đáp án: C Phương pháp giải: Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) có biệt thức \(\Delta = {b^2} - 4ac\) - Nếu \(\Delta < 0\) thì với mọi \(x,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta = 0\)thì \(f\left( x \right)\) có nghiệm kép \(x = - \frac{b}{{2a}}\), với mọi \(x \ne - \frac{b}{{2a}},\,\,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta > 0\),\(f\left( x \right)\)có 2 nghiệm \({x_1},{x_2}\,\,\left( {{x_1} < {x_2}} \right)\) và luôn cùng dấu với hệ số a với mọi x ngoài khoảng \(\left( {{x_1};\,{x_2}} \right)\) và luôn trái dấu với hệ số a với mọi x trong khoảng \(\left( {{x_1};\,{x_2}} \right).\) Lời giải chi tiết: \(f\left( x \right) = {x^2} - 8x + 16\) có \(\left\{ \begin{array}{l}a = 1 > 0\\\Delta ' = {4^2} - 16 = 0\end{array} \right.\) \( \Rightarrow f\left( x \right) \ge 0\) với mọi \(x \in \mathbb{R}\) Chọn C. Quảng cáo
|