Phương pháp giải:

Lời giải chi tiết:

Phương pháp giải:

Lời giải chi tiết:

Phương pháp giải:

Lời giải chi tiết:

Phương pháp giải:

Lời giải chi tiết:

Phương pháp giải:

Lời giải chi tiết:

Phương pháp giải:

1. Thay \(x = 9\) vào biểu thức A.

2. Chứng minh hiệu \(B - \frac{1}{{\sqrt x  - 5}} = 0\).

Lời giải chi tiết:

1. Với \(x = 9\) thỏa mãn điều kiện \(x \ge 0,x \ne 25\), ta có \(A = \frac{{\sqrt x  + 2}}{{\sqrt x  - 5}} = \frac{{\sqrt 9  + 2}}{{\sqrt 9  - 5}} = \frac{{3 + 2}}{{3 - 5}} =  - \frac{5}{2}\)  

Vậy \(A =  - \frac{5}{2}\)

2. Xét hiệu \(B - \frac{1}{{\sqrt x  - 5}}\), ta có

\(\begin{array}{l}\frac{3}{{\sqrt x  + 5}} + \frac{{20 - 2\sqrt x }}{{x - 25}} - \frac{1}{{\sqrt x  - 5}}\\ = \frac{3}{{\sqrt x  + 5}} - \frac{1}{{\sqrt x  - 5}} + \frac{{20 - 2\sqrt x }}{{x - 25}}\\ = \frac{{3\left( {\sqrt x  - 5} \right) - \left( {\sqrt x  + 5} \right)}}{{\left( {\sqrt x  - 5} \right)\left( {\sqrt x  + 5} \right)}} + \frac{{20 - 2\sqrt x }}{{\left( {\sqrt x  - 5} \right)\left( {\sqrt x  + 5} \right)}}\\ =  - \frac{{20 - 2\sqrt x }}{{\left( {\sqrt x  - 5} \right)\left( {\sqrt x  + 5} \right)}} + \frac{{20 - 2\sqrt x }}{{\left( {\sqrt x  - 5} \right)\left( {\sqrt x  + 5} \right)}} = 0\end{array}\)

Vậy \(\frac{3}{{\sqrt x  + 5}} + \frac{{20 - 2\sqrt x }}{{x - 25}}\)\( = \frac{1}{{\sqrt x  - 5}}\)hay B\( = \frac{1}{{\sqrt x  - 5}}\)

Phương pháp giải:

1. Sử dụng hằng đẳng thức, phân tích thành nhân tử và rút gọn.

2. \(f\left( x \right).g\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}f\left( x \right) > 0\\g\left( x \right) > 0\end{array} \right.\\\left\{ \begin{array}{l}f\left( x \right) < 0\\g\left( x \right) < 0\end{array} \right.\end{array} \right.\)

Lời giải chi tiết:

1. Rút gọn biểu thức A

ĐK \(x > 0\). 

Ta có:

\(\begin{array}{l}A = \frac{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}{{\sqrt x \left( {\sqrt x  + 1} \right)\left( {x - \sqrt x  + 1} \right)}}:\frac{1}{{\sqrt x \left( {x\sqrt x  + 1} \right)}}\\A = \frac{{\sqrt x  - 1}}{{\sqrt x \left( {x - \sqrt x  + 1} \right)}}.\sqrt x \left( {x\sqrt x  + 1} \right)\\A = \frac{{\left( {\sqrt x  - 1} \right)\left( {x\sqrt x  + 1} \right)}}{{x - \sqrt x  + 1}}\\A = \frac{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)\left( {x - \sqrt x  + 1} \right)}}{{x - \sqrt x  + 1}}\\A = \left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right) = x - 1\end{array}\)

Vậy \(A = x - 1\).

2. Ta có :

 \(\begin{array}{l}A\left( {\sqrt x  + 1} \right) > 0 \Leftrightarrow \left( {x - 1} \right)\left( {\sqrt x  + 1} \right) > 0\\Do\,\,\sqrt x  + 1 > 0 \Rightarrow x - 1 > 0 \Leftrightarrow x > 1\end{array}\)

Vậy \(x > 1.\)

Phương pháp giải:

Quy đồng mẫu số của biểu thức hoặc rút gọn phân thức bằng hằng đẳng thức \(a - 1 = \left( {\sqrt a  + 1} \right)\left( {\sqrt a  - 1} \right)\,\,\,\,\left( {a > 0} \right)\)

Lời giải chi tiết:

Rút gọn biểu thức \(P = \frac{{a - 1}}{{\sqrt a  + 1}} - \sqrt a  + 11\) với \(a > 0.\)

\(\begin{array}{l}P = \frac{{a - 1}}{{\sqrt a  + 1}} - \sqrt a  + 11\\\,\,\,\,\, = \frac{{\left( {\sqrt a  + 1} \right)\left( {\sqrt a  - 1} \right)}}{{\sqrt a  + 1}} - \sqrt a  + 11\\\,\,\,\,\, = \sqrt a  - 1 - \sqrt a  + 11\\\,\,\,\,\, = 10\end{array}\)

Vậy \(P = 10.\)

Chọn B.

Phương pháp giải:

Áp dụng công thức: \(\sqrt {{A^2}}  = \left[ \begin{array}{l}A\,\,\,\,khi\,\,\,\,A \ge 0\\ - A\,\,\,\,khi\,\,\,\,A < 0\end{array} \right.\)

Lời giải chi tiết:

+) Đáp án A: \(\sqrt {\frac{6}{{{{\left( { - 5} \right)}^2}}}}  = \frac{{\sqrt 6 }}{{ - \left( { - 5} \right)}} = \frac{{\sqrt 6 }}{5}\)\( \Rightarrow \) A sai.                    

+) Đáp án B: \(\sqrt {\frac{2}{a}}  = \frac{{\sqrt 2 }}{{\left| a \right|}} = \left[ \begin{array}{l}\frac{{\sqrt 2 }}{a}\,\,\,\,khi\,\,\,\,a > 0\\\frac{{\sqrt 2 }}{{ - a}}\,\,\,\,khi\,\,\,\,a < 0\end{array} \right.\)\( \Rightarrow \) B sai.

+) Đáp án C: Đúng.                                                               

+) Đáp án D: \(\sqrt {\frac{{16}}{{{a^2}}}}  = \frac{4}{{\left| a \right|}} = \left[ \begin{array}{l}\frac{4}{a}\,\,\,khi\,\,\,\,a > 0\\\frac{4}{{ - a}}\,\,\,\,khi\,\,\,\,a < 0\end{array} \right.\)\( \Rightarrow \) D sai.

Chọn C

Phương pháp giải:

Quy đồng và rút gọn biểu thức.

Lời giải chi tiết:

Điều kiện: \(x \ge 0,\,\,x \ne 1.\)

\(\begin{array}{l}A = \frac{{x + \sqrt x  + 1}}{{x + \sqrt x  - 2}} + \frac{1}{{\sqrt x  - 1}} + \frac{1}{{\sqrt x  + 2}}\,\,\\\,\,\,\, = \frac{{x + \sqrt x  + 1 + \sqrt x  + 2 + \sqrt x  - 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\\\,\,\,\, = \frac{{x + 3\sqrt x  + 2}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}\\\,\,\,\, = \frac{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}} = \frac{{\sqrt x  + 1}}{{\sqrt x  - 1}}.\end{array}\)

Chọn A.

Phương pháp giải:

Quy đồng mẫu các phân thức sau đó rút gọn biểu thức.

Lời giải chi tiết:

\(A = \left[ {\frac{{2\left( {x - 2\sqrt x  + 1} \right)}}{{x - 4}} - \frac{{2\sqrt x  - 1}}{{\sqrt x  + 2}}} \right]:\frac{{\sqrt x }}{{\sqrt x  - 2}}\) với \(x > 0;x \ne 4\)

\(\begin{array}{l}A = \left[ {\frac{{2\left( {x - 2\sqrt x  + 1} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}} - \frac{{\left( {2\sqrt x  - 1} \right)\left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}} \right]:\frac{{\sqrt x }}{{\sqrt x  - 2}}\\\,\,\,\,\, = \frac{{2x - 4\sqrt x  + 2 - 2x + \sqrt x  + 4\sqrt x  - 2}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}.\frac{{\sqrt x  - 2}}{{\sqrt x }}\\\,\,\,\,\, = \frac{{\sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}.\frac{{\sqrt x  - 2}}{{\sqrt x }} = \frac{1}{{\sqrt x  + 2}}\end{array}\)

Vậy \(A = \frac{1}{{\sqrt x  + 2}}\).

Chọn D.

Phương pháp giải:

Sử dụng công thức \(\sqrt {{A^2}B}  = \left| A \right|\sqrt B  = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right.;\,\,\sqrt {AB}  = \sqrt A .\sqrt B \) rồi đặt nhân tử chung của tử số và rút gọn biểu thức.

Lời giải chi tiết:

\(\begin{array}{l}A = \frac{{4 + \sqrt 8  + \sqrt 2  - \sqrt 3  - \sqrt 6 }}{{2 + \sqrt 2  - \sqrt 3 }} = \frac{{4 + 2\sqrt 2  + \sqrt 2  - \sqrt 3  - \sqrt {2.3} }}{{2 + \sqrt 2  - \sqrt 3 }}\\\,\,\,\,\, = \frac{{4 + 3\sqrt 2  - \sqrt 3  - \sqrt {2.3} }}{{2 + \sqrt 2  - \sqrt 3 }} = \frac{{\left( {2 + \sqrt 2  - \sqrt 3 } \right) + \left( {2\sqrt 2  + 2 - \sqrt {2.3} } \right)}}{{2 + \sqrt 2  - \sqrt 3 }}\\\,\,\,\,\, = \frac{{2 + \sqrt 2  - \sqrt 3 }}{{2 + \sqrt 2  - \sqrt 3 }} + \frac{{\sqrt 2 \left( {2 + \sqrt 2  - \sqrt 3 } \right)}}{{2 + \sqrt 2  - \sqrt 3 }} = 1 + \sqrt 2 \end{array}\)

Vậy \(A = 1 + \sqrt 2 \).

Chọn A.

Phương pháp giải:

+) Tìm điều kiện xác định của biểu thức.

+) Quy đồng mẫu, biến đổi và rút gọn biểu thức.

+) Biến đổi \(x\) sau đó thay giá trị của \(x\) thỏa mãn điều kiện và tính giá trị của biểu thức.

+) Giải bất phương trình \(A < 0\) để tìm \(x,\) đối chiếu với điều kiện rồi kết luận.

Lời giải chi tiết:

a) Rút gọn biểu thức \(A.\)

Điều kiện \(x > 0,x \ne 4\)

\(\begin{array}{l}A = \left( {\frac{1}{{\sqrt x }} - \frac{{\sqrt x  - 1}}{{x + 2\sqrt x }}} \right):\left( {\frac{1}{{\sqrt x  + 2}} - \frac{{\sqrt x  + 1}}{{x - 4}}} \right)\\\,\,\,\,\, = \left( {\frac{{\sqrt x  + 2}}{{\sqrt x \left( {\sqrt x  + 2} \right)}} - \frac{{\sqrt x  - 1}}{{\sqrt x \left( {\sqrt x  + 2} \right)}}} \right):\left( {\frac{{\sqrt x  - 2}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}} - \frac{{\sqrt x  + 1}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}} \right)\\\,\,\,\, = \frac{3}{{\sqrt x \left( {\sqrt x  + 2} \right)}}:\frac{{ - 3}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}} = \frac{3}{{\sqrt x \left( {\sqrt x  + 2} \right)}}.\frac{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}{{ - 3}}\\\,\,\,\, = \frac{{2 - \sqrt x }}{{\sqrt x }}\end{array}\)

Vậy với \(x > 0,x \ne 4\)  thì \(A = \frac{{2 - \sqrt x }}{{\sqrt x }}\) .

b) Tính giá trị khi \(x = 9 - 4\sqrt 5 \)

Điều kiện \(x > 0,x \ne 4\)

\(\begin{array}{l}x = 9 - 4\sqrt 5  = {\left( {\sqrt 5 } \right)^2} - 2.2.\sqrt 5  + {2^2} = {\left( {\sqrt 5  - 2} \right)^2}\\ \Rightarrow \sqrt x  = \sqrt {{{\left( {\sqrt 5  - 2} \right)}^2}}  = \left| {\sqrt 5  - 2} \right| = \sqrt 5  - 2\left( {do\,\,\sqrt 5  - 2 > 0\,} \right)\end{array}\)

Thay \(x = 9 - 4\sqrt 5 \,\,\,\left( {tm} \right)\) vào biểu thức ta được:

\(A = \frac{{2 - \sqrt x }}{{\sqrt x }} = \frac{{2 - \left( {\sqrt 5  - 2} \right)}}{{\sqrt 5  - 2}} = \frac{{4 - \sqrt 5 }}{{\sqrt 5  - 2}} = \frac{{\left( {4 - \sqrt 5 } \right)\left( {\sqrt 5  + 2} \right)}}{{{{\left( {\sqrt 5 } \right)}^2} - {2^2}}} = \frac{{4\sqrt 5  + 8 - 5 - 2\sqrt 5 }}{1} = 2\sqrt 5  + 3.\)

Vậy với \(x = 9 - 4\sqrt 5 \) thì  \(A = 2\sqrt 5  + 3.\)

c) Tìm \(x\) để \(A < 0.\)

Điều kiện \(x > 0,x \ne 4\)

 Ta có: \(A < 0 \Leftrightarrow \frac{{2 - \sqrt x }}{{\sqrt x }} < 0\)

Với \(x > 0,x \ne 4\) ta có: \(\sqrt x  > 0\)

\( \Rightarrow \frac{{2 - \sqrt x }}{{\sqrt x }} < 0 \Leftrightarrow 2 - \sqrt x  < 0 \Leftrightarrow \sqrt x  > 2 \Leftrightarrow x > 4.\) thì  \(2 - \sqrt x  < 0 \Leftrightarrow \sqrt x  > 2 \Leftrightarrow x > 4\)

Kết hợp với điều kiện ta được \(x > 4\) thì \(A < 0.\)  

Phương pháp giải:

+) Tìm điều kiện của \(x\) để biểu thức xác định.

+) Giải bất phương trình \(A < 0\) để tìm \(x,\) đối chiếu với điều kiện rồi kết luận.

Lời giải chi tiết:

a) Rút gọn biểu thức \(A.\)

Điều kiện: \(\left\{ \begin{array}{l}x \ge 0\\\sqrt x  - 2 \ne 0\\3 - \sqrt x  \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\x \ne 4\\x \ne 9\end{array} \right..\)

\(\begin{array}{l}A = \left( {1 - \frac{{\sqrt x }}{{1 + \sqrt x }}} \right):\left( {\frac{{\sqrt x  + 3}}{{\sqrt x  - 2}} + \frac{{\sqrt x  + 2}}{{3 - \sqrt x }} + \frac{{\sqrt x  + 2}}{{x - 5\sqrt x  + 6}}} \right)\\ = \frac{{1 + \sqrt x  - \sqrt x }}{{1 + \sqrt x }}:\left( {\frac{{\sqrt x  + 3}}{{\sqrt x  - 2}} + \frac{{\sqrt x  + 2}}{{3 - \sqrt x }} + \frac{{\sqrt x  + 2}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}} \right)\\ = \frac{1}{{1 + \sqrt x }}:\left( {\frac{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}} - \frac{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}} + \frac{{\sqrt x  + 2}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}} \right)\\ = \frac{1}{{1 + \sqrt x }}:\frac{{x - 9 - x + 4 + \sqrt x  + 2}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}\\ = \frac{1}{{1 + \sqrt x }}.\frac{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}{{\sqrt x  - 3}}\\ = \frac{{\sqrt x  - 2}}{{\sqrt x  + 1}}\end{array}\)

b) Tìm \(x\) để \(A < 0.\)

Với  \(x \ge 0;x \ne 9;x \ne 4\)  ta có: \(A = \frac{{\sqrt x  - 2}}{{\sqrt x  + 1}}\)

Ta có: \(A < 0 \Leftrightarrow \frac{{\sqrt x  - 2}}{{\sqrt x  + 1}} < 0\).

Vì  \(\sqrt x  + 1 > 0,\forall x \ge 0 \Rightarrow A < 0 \Leftrightarrow \sqrt x  - 2 < 0 \Leftrightarrow \sqrt x  < 2 \Leftrightarrow x < 4\)  

Kết hợp với điều kiện \(x \ge 0;x \ne 9;x \ne 4\)  ta được: \(0 \le x < 4\) thì  \(A < 0.\)

Phương pháp giải:

+) Quy đồng mẫu các phân thức và biến đổi, rút gọn biểu thức.

+) Giải phương trình \(2P = 2\sqrt x  + 5,\) tìm \(x\) sau đó đối chiếu với điều kiện rồi kết luận.

Lời giải chi tiết:

a) Chứng minh rằng \(P = \frac{{\sqrt x  + 1}}{{\sqrt x }}\)

Điều kiện:  \(x > 0,x \ne 1\)

\(\begin{array}{l}P = \left( {\frac{{x - 2}}{{x + 2\sqrt x }} + \frac{1}{{\sqrt x  + 2}}} \right).\frac{{\sqrt x  + 1}}{{\sqrt x  - 1}}\, = \left( {\frac{{x - 2}}{{\sqrt x \left( {\sqrt x  + 2} \right)}} + \frac{1}{{\sqrt x  + 2}}} \right).\frac{{\sqrt x  + 1}}{{\sqrt x  - 1}}\\\,\,\,\,\, = \left( {\frac{{x - 2}}{{\sqrt x \left( {\sqrt x  + 2} \right)}} + \frac{{\sqrt x }}{{\sqrt x \left( {\sqrt x  + 2} \right)}}} \right).\frac{{\sqrt x  + 1}}{{\sqrt x  - 1}} = \frac{{x - 2 + \sqrt x }}{{\sqrt x \left( {\sqrt x  + 2} \right)}}.\frac{{\sqrt x  + 1}}{{\sqrt x  - 1}}\\\,\,\,\, = \frac{{x + 2\sqrt x  - \sqrt x  - 2}}{{\sqrt x \left( {\sqrt x  + 2} \right)}}.\frac{{\sqrt x  + 1}}{{\sqrt x  - 1}} = \frac{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}{{\sqrt x \left( {\sqrt x  + 2} \right)}}.\frac{{\sqrt x  + 1}}{{\sqrt x  - 1}}\\\,\,\,\, = \frac{{\sqrt x  + 1}}{{\sqrt x }}.\end{array}\)

Vậy với \(x > 0,x \ne 1\) ta có  \(P = \frac{{\sqrt x  + 1}}{{\sqrt x }}.\)

b) Tìm \(x\)  để \(2P = 2\sqrt x  + 5\)

Điều kiện: \(x > 0,x \ne 1\)

\(\begin{array}{l}\,\,\,\,\,\,2P = 2\sqrt x  + 5 \Leftrightarrow 2.\frac{{\sqrt x  + 1}}{{\sqrt x }} = 2\sqrt x  + 5\\ \Leftrightarrow 2\sqrt x  + 2 = 2x + 5\sqrt x  \Leftrightarrow 2x + 3\sqrt x  - 2 = 0\\ \Leftrightarrow 2x - \sqrt x  + 4\sqrt x  - 2 = 0 \Leftrightarrow \sqrt x \left( {2\sqrt x  - 1} \right) + 2\left( {2\sqrt x  - 1} \right) = 0\\ \Leftrightarrow \left( {2\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}\sqrt x  = \frac{1}{2}\\\sqrt x  =  - 2\,\,\,\,\left( {VN} \right)\end{array} \right. \Leftrightarrow x = \frac{1}{4}\,\,\,\left( {tm} \right)\end{array}\)

Vậy \(x = \frac{1}{4}\) thì \(2P = 2\sqrt x  + 5.\)

Phương pháp giải:

+) Tìm điều kiện xác định của biểu thức.

+) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức.

+) Thay giá trị \(x\,\,\left( {tmdk} \right)\) vào biểu thức đã được rút gọn và tính giá trị của biểu thức.

+) Giải bất phương trình \(P <  - \frac{1}{2},\) tìm \(x\) sau đó đối chiếu với điều kiện rồi kết luận.

Lời giải chi tiết:

a) Rút gọn \(P.\)

Điều kiện xác định: \(x \ge 0,x \ne 9\)

\(\begin{array}{l}P = \left( {\frac{{2\sqrt x }}{{\sqrt x  + 3}} + \frac{{\sqrt x }}{{\sqrt x  - 3}} - \frac{{3x + 3}}{{x - 9}}} \right):\left( {\frac{{2\sqrt x  - 2}}{{\sqrt x  - 3}} - 1} \right)\\ = \left( {\frac{{2\sqrt x \left( {\sqrt x  - 3} \right)}}{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right)}} + \frac{{\sqrt x \left( {\sqrt x  + 3} \right)}}{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right)}} - \frac{{3x + 3}}{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right)}}} \right):\left( {\frac{{2\sqrt x  - 2}}{{\sqrt x  - 3}} - \frac{{\sqrt x  - 3}}{{\sqrt x  - 3}}} \right)\\ = \frac{{2x - 6\sqrt x  + x + 3\sqrt x  - 3x - 3}}{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right)}}:\frac{{2\sqrt x  - 2 - \sqrt x  + 3}}{{\sqrt x  - 3}}\\ = \frac{{ - 3\left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right)}}.\frac{{\sqrt x  - 3}}{{\sqrt x  + 1}}\\ = \frac{{ - 3}}{{\sqrt x  + 3}}.\end{array}\)

b) Tính giá trị của biểu thức \(P\) biết \(x = \frac{{3 - \sqrt 5 }}{2}\)

Ta có: \(x = \frac{{3 - \sqrt 5 }}{2}\,\,\,\left( {tmdk} \right) \Rightarrow \sqrt x  = \sqrt {\frac{{3 - \sqrt 5 }}{2}}  = \frac{{\sqrt {6 - 2\sqrt 5 } }}{2} = \frac{{\sqrt {{{\left( {\sqrt 5  - 1} \right)}^2}} }}{2} = \frac{{\sqrt 5  - 1}}{2}\)

Khi đó ta có: \(P = \frac{{ - 3}}{{\sqrt x  + 3}} = \frac{{ - 3}}{{\frac{{\sqrt 5  - 1}}{2} + 3}} = \frac{{ - 6}}{{\sqrt 5  + 5}} = \frac{{3\left( {\sqrt 5  - 5} \right)}}{{10}}\)

c) Tìm \(x\)  để \(P < \frac{{ - 1}}{2}\)

Điều kiện xác định: \(x \ge 0,x \ne 9\)

Ta có: \(P = \frac{{ - 3}}{{\sqrt x  + 3}} < \frac{{ - 1}}{2} \Leftrightarrow \frac{3}{{\sqrt x  + 3}} > \frac{1}{2} \Leftrightarrow \frac{6}{{2\left( {\sqrt x  + 3} \right)}} - \frac{{\sqrt x  + 3}}{{2\left( {\sqrt x  + 3} \right)}} > 0 \Leftrightarrow \frac{{3 - \sqrt x }}{{2\left( {\sqrt x  + 3} \right)}} > 0\)

Với \(x \ge 0,x \ne 9\) ta có: \(2\left( {\sqrt x  + 3} \right) > 0\) .

Khi đó để \(P < \frac{{ - 1}}{2} \Leftrightarrow 3 - \sqrt x  > 0 \Leftrightarrow \sqrt x  < 3 \Leftrightarrow x < 9.\)

Vậy kết hợp điều kiện ta được: \(0 \le x < 9\)  thì \(P < \frac{{ - 1}}{2}.\)

Phương pháp giải:

+) Đặt điều kiện xác định của biểu thức.

+) Quy đồng mẫu, biến đổi các biểu thức sau đó rút gọn biểu thức đã cho.

+) Xét hiệu \(P - 3,\) so sánh hiệu đó với \(0\) rồi kết luận.

Lời giải chi tiết:

a) Rút gọn \(P.\)

Điều kiện xác định: \(x \ne 1;x > 0\)

\(\begin{array}{l}P = 1:\left( {\frac{{x + 2}}{{x\sqrt x  - 1}} + \frac{{\sqrt x  + 1}}{{x + \sqrt x  + 1}} - \frac{{\sqrt x  + 1}}{{x - 1}}} \right)\\ = 1:\left( {\frac{{x + 2}}{{\left( {\sqrt x  - 1} \right)\left( {x + \sqrt x  + 1} \right)}} + \frac{{\sqrt x  + 1}}{{\left( {x + \sqrt x  + 1} \right)}} - \frac{{\sqrt x  + 1}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}} \right)\\ = 1:\frac{{\left( {x + 2} \right)\left( {\sqrt x  + 1} \right) + {{\left( {\sqrt x  + 1} \right)}^2}\left( {\sqrt x  - 1} \right) - \left( {\sqrt x  + 1} \right)\left( {x + \sqrt x  + 1} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)\left( {x + \sqrt x  + 1} \right)}}\\ = 1:\frac{{x\sqrt x  + x + 2\sqrt x  + 2 + x\sqrt x  + x - \sqrt x  - 1 - \left( {x\sqrt x  + x + \sqrt x  + x + \sqrt x  + 1} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)\left( {x + \sqrt x  + 1} \right)}}\\ = \frac{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)\left( {x + \sqrt x  + 1} \right)}}{{x\sqrt x  - \sqrt x }}\\ = \frac{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)\left( {x + \sqrt x  + 1} \right)}}{{\sqrt x \left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\\ = \frac{{x + \sqrt x  + 1}}{{\sqrt x }}.\end{array}\)

 b) So sánh \(P\)  với \(3.\)

Điều kiện xác định: \(x \ne 1;x > 0\)

Xét  hiệu:  \(P - 3 = \frac{{x + \sqrt x  + 1}}{{\sqrt x }} - 3 = \frac{{x + \sqrt x  + 1 - 3\sqrt x }}{{\sqrt x }} = \frac{{{{\left( {\sqrt x  - 1} \right)}^2}}}{{\sqrt x }}\)

Với \(x \ne 1;x > 0\) ta có: \(\sqrt x  > 0;\,\,{\left( {\sqrt x  - 1} \right)^2} > 0 \Rightarrow P - 3 > 0 \Leftrightarrow P > 3.\)

Phương pháp giải:

+) Tìm điều kiện xác định của biểu thức.

+) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức.

+) Giải phương trình \(P = \frac{1}{2},\) tìm \(x\) rồi đối chiều với điều kiện sau đó kết luận.

+) Dựa vào điều kiện của \(x\) để chứng mình \(P \le \frac{2}{3}.\)

Lời giải chi tiết:

\(P = \frac{{15\sqrt x  - 11}}{{x + 2\sqrt x  - 3}} + \frac{{3\sqrt x  - 2}}{{1 - \sqrt x }} - \frac{{2\sqrt x  + 3}}{{\sqrt x  + 3}}\)

a) Rút gọn \(P.\)

Điều kiện \(x \ge 0,x \ne 1\)

\(\begin{array}{l}P = \frac{{15\sqrt x  - 11}}{{x + 2\sqrt x  - 3}} + \frac{{3\sqrt x  - 2}}{{1 - \sqrt x }} - \frac{{2\sqrt x  + 3}}{{\sqrt x  + 3}}\\ = \frac{{15\sqrt x  - 11}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right)}} - \frac{{3\sqrt x  - 2}}{{\sqrt x  - 1}} - \frac{{2\sqrt x  + 3}}{{\sqrt x  + 3}}\\ = \frac{{15\sqrt x  - 11}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right)}} - \frac{{\left( {3\sqrt x  - 2} \right)\left( {\sqrt x  + 3} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right)}} - \frac{{\left( {2\sqrt x  + 3} \right)\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right)}}\\ = \frac{{15\sqrt x  - 11 - \left( {3x + 9\sqrt x  - 2\sqrt x  - 6} \right) - \left( {2x - 2\sqrt x  + 3\sqrt x  - 3} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right)}}\\ = \frac{{15\sqrt x  - 11 - 3x - 7\sqrt x  + 6 - 2x - \sqrt x  + 3}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right)}}\\ = \frac{{ - 5x + 7\sqrt x  - 2}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right)}} = \frac{{\left( { - 5\sqrt x  + 2} \right)\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right)}} = \frac{{ - 5\sqrt x  + 2}}{{\sqrt x  + 3}}.\end{array}\)

b) Tìm các giá trị của \(x\)  để  \(P = \frac{1}{2}.\)

Với điều kiện \(x \ge 0,x \ne 1.\) ta có:

\(\begin{array}{l}P = \frac{1}{2} \Leftrightarrow \frac{{ - 5\sqrt x  + 2}}{{\sqrt x  + 3}} = \frac{1}{2} \Leftrightarrow 2\left( { - 5\sqrt x  + 2} \right) = \sqrt x  + 3\\ \Leftrightarrow  - 10\sqrt x  + 4 - \sqrt x  - 3 = 0\\ \Leftrightarrow  - 11\sqrt x  =  - 1 \Leftrightarrow x = \frac{1}{{121}}\,\,\,\,\left( {tm} \right).\end{array}\)

Vậy \(x = \frac{1}{{121}}\)  thì  \(P = \frac{1}{2}.\)

c) Chứng minh \(P \le \frac{2}{3}\)

Ta có: \(P = \frac{{ - 5\sqrt x  + 2}}{{\sqrt x  + 3}}\)

Với  \(x \ge 0,\,\,x \ne 1\)  ta có: \(\sqrt x  + 3 \ge 3\)

\(5\sqrt x  \ge 0 \Rightarrow  - 5\sqrt x  \le 0 \Rightarrow  - 5\sqrt x  + 2 \le 2\)

Khi đó ta có: \(P \le \frac{2}{3}\)

Vậy \(x \ge 0,x \ne 1\) thì  \(P \le \frac{2}{3}.\)

Phương pháp giải:

+) Tìm điều kiện xác định của biểu thức.

+) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức.

+) Biến đổi \(x,\) thay giá trị \(x = 7 - 4\sqrt 3 \,\,\,\left( {tm} \right)\) vào biểu thức \(P\) rồi tính giá trị biểu thức.

Lời giải chi tiết:

a) Rút gọn \(P.\)

Điều kiện: \(x \ge 0;x \ne 1\)

\(\begin{array}{l}P = \left( {\frac{1}{{\sqrt x  + 1}} - \frac{{2\sqrt x  - 2}}{{x\sqrt x  - \sqrt x  + x - 1}}} \right):\left( {\frac{1}{{\sqrt x  - 1}} - \frac{2}{{x - 1}}} \right)\\ = \left( {\frac{1}{{\sqrt x  + 1}} - \frac{{2\left( {\sqrt x  - 1} \right)}}{{\sqrt x \left( {x - 1} \right) + x - 1}}} \right):\left( {\frac{1}{{\sqrt x  - 1}} - \frac{2}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}} \right)\\ = \left( {\frac{1}{{\left( {\sqrt x  + 1} \right)}} - \frac{{2\left( {\sqrt x  - 1} \right)}}{{\left( {x - 1} \right)\left( {\sqrt x  + 1} \right)}}} \right):\left( {\frac{{\sqrt x  + 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}} - \frac{2}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}} \right)\\ = \left( {\frac{{\sqrt x  + 1}}{{{{\left( {\sqrt x  + 1} \right)}^2}}} - \frac{2}{{{{\left( {\sqrt x  + 1} \right)}^2}}}} \right):\frac{{\sqrt x  - 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\\ = \frac{{\sqrt x  - 1}}{{{{\left( {\sqrt x  + 1} \right)}^2}}}.\frac{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}{{\sqrt x  - 1}}\\ = \frac{{\sqrt x  - 1}}{{\sqrt x  + 1}}.\end{array}\)

b) Tính giá trị của P khi \(x = 7 - 4\sqrt 3 \)

Khi \(x = 7 - 4\sqrt 3  = {\left( {2 - \sqrt 3 } \right)^2}\,\,\,\,\left( {tm} \right) \Rightarrow \sqrt x  = \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}}  = \left| {2 - \sqrt 3 } \right| = 2 - \sqrt 3 \)

Ta có: \(P = \frac{{2 - \sqrt 3  - 1}}{{2 - \sqrt 3  + 1}} = \frac{{1 - \sqrt 3 }}{{3 - \sqrt 3 }} = \frac{{\left( {1 - \sqrt 3 } \right)\left( {3 + \sqrt 3 } \right)}}{{{3^2} - 3}} = \frac{{ - 2\sqrt 3 }}{6} = \frac{{ - \sqrt 3 }}{3}.\)

Phương pháp giải:

+) Tìm điều kiện xác định của biểu thức.

+) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức.

+) Giải phương trình \(A = 4,\) tìm \(x\) rồi đối chiều với điều kiện sau đó kết luận.

Lời giải chi tiết:

\(A = \sqrt {x + 4\sqrt {x - 4} }  + \sqrt {x - 4\sqrt {x - 4} } \)

a) Rút gọn \(A.\)

Điều kiện \(x \ge 4\)

Ta có:

\(\begin{array}{l}A = \sqrt {x + 4\sqrt {x - 4} }  + \sqrt {x - 4\sqrt {x - 4} } \\ = \sqrt {4 + x - 4 + 4\sqrt {x - 4} }  + \sqrt {4 + x - 4 - 4\sqrt {x - 4} } \\ = \sqrt {{{\left( {\sqrt {x - 4}  + 2} \right)}^2}}  + \sqrt {{{\left( {\sqrt {x - 4}  - 2} \right)}^2}} \\ = \left| {\sqrt {x - 4}  + 2} \right| + \left| {\sqrt {x - 4}  - 2} \right|\\ = \sqrt {x - 4}  + 2 + \left| {\sqrt {x - 4}  - 2} \right|\end{array}\)

TH1: \(\sqrt {x - 4}  - 2 \ge 0 \Leftrightarrow x \ge 8.\)  Ta có:\(A = \sqrt {x - 4}  + 2 + \sqrt {x - 4}  - 2 = 2\sqrt {x - 4} \)

TH2: \(\sqrt {x - 4}  - 2 < 0 \Leftrightarrow x < 8\). Ta có: \(A = \sqrt {x - 4}  + 2 - \sqrt {x - 4}  + 2 = 4\)

Vậy \(x \ge 8\)  thì \(A = 2\sqrt {x - 4} \)

Với \(4 \le x < 8\)  thì  \(A = 4.\)

b) Tìm \(x\)  để  \(A = 4.\)

Theo câu a) ta có TH1: Với \(4 \le x < 8\)  thì \(A = 4.\)

Với TH2: \(x \ge 8\)

\(A = 4 \Leftrightarrow 2\sqrt {x - 4}  = 4 \Leftrightarrow x - 4 = 4 \Leftrightarrow x = 8\)

Vậy \(x = 8\)  thì  \(A = 4.\)

Kết hợp 2 trường hợp ta được \(4 \le x \le 8\) thì \(A = 4.\)

Phương pháp giải:

+) Tìm điều kiện xác định của biểu thức.

+) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức.

+) Dựa vào điều kiện của \(x\) để chứng mình \(A \ge 0.\)

Lời giải chi tiết:

a) Với \(x \ge 0,y \ge 0,x \ne y\). Ta có: 
\(\begin{array}{l}A = \left( {\frac{{x - y}}{{\sqrt x  - \sqrt y }} + \frac{{\sqrt {{x^3}}  - \sqrt {{y^3}} }}{{y - x}}} \right):\frac{{{{\left( {\sqrt x  - \sqrt y } \right)}^2} + \sqrt {xy} }}{{\sqrt x  + \sqrt y }}\\ = \left( {\frac{{\left( {\sqrt x  - \sqrt y } \right)\left( {\sqrt x  + \sqrt y } \right)}}{{\sqrt x  - \sqrt y }} - \frac{{\left( {\sqrt x  - \sqrt y } \right)\left( {x + \sqrt {xy}  + y} \right)}}{{\left( {\sqrt x  - \sqrt y } \right)\left( {\sqrt x  + \sqrt y } \right)}}} \right):\frac{{{{\left( {\sqrt x  - \sqrt y } \right)}^2} + \sqrt {xy} }}{{\sqrt x  + \sqrt y }}\\ = \left( {\sqrt x  + \sqrt y  - \frac{{x + \sqrt {xy}  + y}}{{\sqrt x  + \sqrt y }}} \right):\frac{{x - \sqrt {xy}  + y}}{{\sqrt x  + \sqrt y }}\\ = \frac{{{{\left( {\sqrt x  + \sqrt y } \right)}^2} - x - \sqrt {xy}  - y}}{{\sqrt x  + \sqrt y }}.\frac{{\sqrt x  + \sqrt y }}{{x - \sqrt {xy}  + y}}\\ = \frac{{\sqrt {xy} }}{{x - \sqrt {xy}  + y}}\end{array}\)

b) Ta có: \(x \ge 0,y \ge 0,x \ne y\) thì \(\sqrt {xy}  \ge 0;x - \sqrt {xy}  + y = {\left( {\sqrt x  - \sqrt y } \right)^2} + \sqrt {xy}  \ge 0\) .

Vậy \(A \ge 0\) với \(x \ge 0,y \ge 0,x \ne y\).

Phương pháp giải:

Phương  pháp:

* Các bước làm bài toán rút gọn biểu thức:

B1: Tìm ĐKXĐ của bài toán nếu đề bài chưa cho ĐKXĐ. Các biểu thức cần lấy ĐK là:

\(\begin{align}  & +)\,\,\frac{1}{f\left( x \right)}\Rightarrow f\left( x \right)\ne 0. \\ & +)\,\,\sqrt{f\left( x \right)}\Rightarrow f\left( x \right)\ge 0. \\ & +)\,\,\frac{1}{\sqrt{f\left( x \right)}}\Rightarrow f\left( x \right)>0. \\\end{align}\)

B2: Tìm mẫu thức chung của biểu thức sau đó quy đồng mẫu các phân thức.

B3: Rút gọn biểu thức.

* Phương  pháp làm câu b: Tìm x để \(P=a:\)

+) Ta cho biểu thức P vừa rút gọn được bằng giá trị a và giải phương trình tìm x.

+) Đối chiếu giá trị của x vừa tìm được với ĐKXĐ xem x có thỏa mãn không.

+) Nếu x thỏa mãn thì kết luận đó là giá trị cần tìm. Nếu x không thỏa mãn thì loại giá trị đó.

Lời giải chi tiết:

Giải:

Với  \(x\ge 0;x\ne 4;x\ne 9\) ta có

  \(\begin{align}  & P=\frac{2\sqrt{x}-9-\left( \sqrt{x}+3 \right)\left( \sqrt{x}-3 \right)+\left( 2\sqrt{x}+1 \right)\left( \sqrt{x}-2 \right)}{\left( \sqrt{x}-2 \right)\left( \sqrt{x}-3 \right)} \\ & \,\,\,\,=\frac{2\sqrt{x}-9-\left( x-9 \right)+2x-3\sqrt{x}-2}{\left( \sqrt{x}-2 \right)\left( \sqrt{x}-3 \right)}=\frac{x-\sqrt{x}-2}{\left( \sqrt{x}-2 \right)\left( \sqrt{x}-3 \right)} \\  & \,\,\,\,=\frac{\left( \sqrt{x}+1 \right)\left( \sqrt{x}-2 \right)}{\left( \sqrt{x}-3 \right)\left( \sqrt{x}-2 \right)} \\ & \,\,\,\,=\frac{\sqrt{x}+1}{\sqrt{x}-3}. \\ \end{align}\)

Vậy \(P=\frac{\sqrt{x}+1}{\sqrt{x}-3}\) với \(x\ge 0;x\ne 4;x\ne 9\)

b. Theo câu a ta có \(P=\frac{\sqrt{x}+1}{\sqrt{x}-3}\) với \(x\ge 0;x\ne 4;x\ne 9\)

\(\begin{align} & \text{ P }=\text{ 5}\Leftrightarrow \frac{\sqrt{x}+1}{\sqrt{x}-3}=5 \\  & \Rightarrow \sqrt{x}+1=5\left( \sqrt{x}-3 \right) \\  & \Leftrightarrow \sqrt{x}+1=5\sqrt{x}-15 \\ & \Leftrightarrow 16=4\sqrt{x} \\  & \Leftrightarrow \sqrt{x}=\frac{16}{4}=4 \\ & \Leftrightarrow x=16\,\,\,\left( tm \right) \\ \end{align}\)

Vậy để P = 5 thì x = 16.

Phương pháp giải:

Lời giải chi tiết:

\(\begin{array}{l}
\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} - \sqrt {\dfrac{8}{{7 - 3\sqrt 5 }}} \\
= \left| {2 - \sqrt 5 } \right| - \sqrt {\dfrac{{16}}{{14 - 6\sqrt 5 }}} \\
= \left| {2 - \sqrt 5 } \right| - \dfrac{{\sqrt {16} }}{{\sqrt {14 - 6\sqrt 5 } }}\\
= - \left( {2 - \sqrt 5 } \right) - \dfrac{4}{{\sqrt {{3^2} - 2.3.\sqrt 5 + {{\sqrt 5 }^2}} }}\left( {Do{\rm{ }}2 - \sqrt 5 < 0} \right)\\
= - 2 + \sqrt 5 - \dfrac{4}{{\sqrt {{{\left( {3 - \sqrt 5 } \right)}^2}} }}\\
= - 2 + \sqrt 5 - \dfrac{4}{{3 - \sqrt 5 }}\\
= - 2 + \sqrt 5 - \dfrac{{4.\left( {3 + \sqrt 5 } \right)}}{{\left( {3 - \sqrt 5 } \right)\left( {3 + \sqrt 5 } \right)}}\\
= - 2 + \sqrt 5 - \dfrac{{4.\left( {3 + \sqrt 5 } \right)}}{4}\\
= - 2 + \sqrt 5 - 3 - \sqrt 5 = - 5
\end{array}\)

b)

\(\begin{array}{l}
A = \dfrac{x}{{\sqrt x - 1}} - \dfrac{{2x - \sqrt x }}{{x - \sqrt x }}\\
= \dfrac{x}{{\sqrt x - 1}} - \dfrac{{\sqrt x \left( {2\sqrt x - 1} \right)}}{{\sqrt x \left( {\sqrt x - 1} \right)}}\\
= \dfrac{x}{{\sqrt x - 1}} - \dfrac{{2\sqrt x - 1}}{{\sqrt x - 1}}\\
= \dfrac{{x - 2\sqrt x + 1}}{{\sqrt x - 1}}\\
= \dfrac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x - 1}} = \sqrt x - 1
\end{array}\)

Phương pháp giải:

Lời giải chi tiết:

a)     Ta có:

\(\begin{array}{l}A = \left( {\frac{2}{{3 - \sqrt 5 }} + \frac{1}{{2 - \sqrt 5 }} - \frac{{10}}{{2\sqrt 5 }}} \right).\left( {1 - 3\sqrt 5 } \right)\\ = \left( {\frac{{2\left( {3 + \sqrt 5 } \right)}}{{\left( {3 - \sqrt 5 } \right)\left( {3 + \sqrt 5 } \right)}} + \frac{{1.\left( {2 + \sqrt 5 } \right)}}{{\left( {2 + \sqrt 5 } \right)\left( {2 - \sqrt 5 } \right)}} - \frac{5}{{\sqrt 5 }}} \right).\left( {1 - 3\sqrt 5 } \right)\\ = \left( {\frac{{2\left( {3 + \sqrt 5 } \right)}}{4} + \frac{{2 + \sqrt 5 }}{{ - 1}} - \sqrt 5 } \right).\left( {1 - 3\sqrt 5 } \right)\\ = \left( {\frac{{3 + \sqrt 5 }}{2} - \frac{{2 + \sqrt 5 }}{1} - \sqrt 5 } \right).\left( {1 - 3\sqrt 5 } \right)\\ = \left( {\frac{{3 + \sqrt 5  - 2\left( {2 + \sqrt 5 } \right) - 2\sqrt 5 }}{2}} \right).\left( {1 - 3\sqrt 5 } \right)\\= \left( {\frac{{3 + \sqrt 5  - 4 - 2\sqrt 5  - 2\sqrt 5 }}{2}} \right).\left( {1 - 3\sqrt 5 } \right)\\ =  - \left( {\frac{{ - 1 - 3\sqrt 5 }}{2}} \right).\left( {3\sqrt 5  - 1} \right)\\ = \left( {\frac{{3\sqrt 5  + 1}}{2}} \right).\left( {3\sqrt 5  - 1} \right)\\ = \frac{{\left( {3\sqrt 5  + 1} \right)\left( {3\sqrt 5  - 1} \right)}}{2}\\ = \frac{{44}}{2} = 22\end{array}\)

b)      Ta có: 

\(\begin{array}{l}P = \frac{{\sqrt x }}{{2\sqrt x  - 3}} + \frac{{\sqrt x  - 2}}{{2\sqrt x  + 3}} + \frac{{15 - 4\sqrt x }}{{9 - 4x}}\\ = \frac{{\sqrt x }}{{2\sqrt x  - 3}} + \frac{{\sqrt x  - 2}}{{2\sqrt x  + 3}} - \frac{{15 - 4\sqrt x }}{{4x - 9}}\\ = \frac{{\sqrt x }}{{2\sqrt x  - 3}} + \frac{{\sqrt x  - 2}}{{2\sqrt x  + 3}} - \frac{{15 - 4\sqrt x }}{{\left( {2\sqrt x  - 3} \right).\left( {2\sqrt x  + 3} \right)}}\\ = \frac{{\sqrt x .\left( {2\sqrt x  + 3} \right) + \left( {\sqrt x  - 2} \right).\left( {2\sqrt x  - 3} \right) - \left( {15 - 4\sqrt x } \right)}}{{\left( {2\sqrt x  - 3} \right).\left( {2\sqrt x  + 3} \right)}}\\ = \frac{{2x + 3\sqrt x  + 2x - 3\sqrt x  - 4\sqrt x  + 6 - 15 + 4\sqrt x }}{{\left( {2\sqrt x  - 3} \right).\left( {2\sqrt x  + 3} \right)}}\\ = \frac{{4x - 9}}{{4x - 9}}\\ = 1\end{array}\)

Phương pháp giải:

+) Sử dụng hằng đẳng thức: \({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\).

+) Để so sánh a và b ta xét hiệu \(a - b\) .

Lời giải chi tiết:

Cho hai biểu thức: \(A\, = \,\frac{{2\sqrt x  - 4}}{{\sqrt x  - 1}}\) và \(B\, = \,\frac{{\sqrt x }}{{\sqrt x  - 1}} + \frac{3}{{\sqrt x  + 1}} - \frac{{6\sqrt x  - 4}}{{x - 1}}\) với \(x \ge 0,\,\,x \ne 1.\)

1. Tính giá trị của A khi \(x = 4.\)

Khi \(x = 4\) thì \(A\, = \,\frac{{2\sqrt 4  - 4}}{{\sqrt 4  - 1}} = \frac{{2.2 - 4}}{{2 - 1}} = \frac{0}{1} = 0\)

2. Rút gọn B.

\(\begin{array}{l}B\, = \,\frac{{\sqrt x }}{{\sqrt x  - 1}} + \frac{3}{{\sqrt x  + 1}} - \frac{{6\sqrt x  - 4}}{{x - 1}} = \frac{{\sqrt x \left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}} + \frac{{3\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}} - \frac{{6\sqrt x  - 4}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\\\,\,\,\, = \frac{{x + \sqrt x  + 3\sqrt x  - 3 - 6\sqrt x  + 4}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}} = \frac{{x - 2\sqrt x  + 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\\\,\,\,\, = \frac{{{{\left( {\sqrt x  - 1} \right)}^2}}}{{x - 1}} = \frac{{\sqrt x  - 1}}{{\sqrt x  + 1}}.\end{array}\)

3. So sánh A.B với 5. 

\(\begin{array}{l}A.B - 5 = \frac{{2\sqrt x  - 4}}{{\sqrt x  - 1}}.\frac{{\sqrt x  - 1}}{{\sqrt x  + 1}} - 5 = \frac{{2\sqrt x  - 4}}{{\sqrt x  + 1}} - 5\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{2\sqrt x  - 4 - 5\sqrt x  - 5}}{{\sqrt x  + 1}} = \frac{{ - 3\sqrt x  - 9}}{{\sqrt x  + 1}}\end{array}\)

Có \(\sqrt x  \ge 0\;\forall x \ge 0 \Rightarrow  - 3\sqrt x  \le 0\;\forall x \ge 0 \Rightarrow  - 3\sqrt x  - 9 < 0\;\forall x \ge 0\) 

Mặt khác  \(\sqrt x  \ge 0\;\forall x \ge 0 \Rightarrow \sqrt x  + 1 > 0\;\forall x \ge 0.\)

\( \Rightarrow A.B - 5 = \frac{{ - 3\sqrt x  - 9}}{{\sqrt x  + 1}} < 0\;\;\forall x \ge 0 \Rightarrow \,A.B < 5\)

Chọn A.

Phương pháp giải:

+) Tìm điều kiện xác định của biểu thức.

+) Sử dụng biểu thức liên hợp.

+) Đặt nhân tử chung.

+) Rút gọn các phân thức trước khi tiến hành tính toán.

Lời giải chi tiết:

ĐKXĐ: \(x \ge 0\) và \(x \ne 1\)

\(\begin{array}{l}B = \left( {\frac{{2x + 1}}{{\sqrt {{x^3}}  - 1}} - \frac{{\sqrt x }}{{x + \sqrt x  + 1}}} \right).\left( {\frac{{1 + \sqrt {{x^3}} }}{{1 + \sqrt x }} - \sqrt x } \right)\\ = \frac{{2x + 1 - \sqrt x \left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  - 1} \right).\left( {x + \sqrt x  + 1} \right)}}.\left[ {\frac{{\left( {\sqrt x  + 1} \right)\left( {x - \sqrt x  + 1} \right)}}{{\sqrt x  + 1}} - \sqrt x } \right]\\ = \frac{{2x + 1 - x + \sqrt x }}{{\left( {\sqrt x  - 1} \right).\left( {x + \sqrt x  + 1} \right)}}.\left( {1 - 2\sqrt x  + x} \right)\\ = \frac{{x + \sqrt x  + 1}}{{\left( {\sqrt x  - 1} \right).\left( {x + \sqrt x  + 1} \right)}}.{\left( {\sqrt x  - 1} \right)^2} = \sqrt x  - 1\end{array}\)

Ta có \(B = \sqrt x  - 1\)

Với \(x = 9\) thỏa mãn điều kiện suy ra \(B = \sqrt x  - 1 = \sqrt 9  - 1 = 3 - 1 = 2\).

Vậy khi \(x = 9\) thì \(B = 2\).

Phương pháp giải:

+) Tìm điều kiện xác định của biểu thức.

+) Sử dụng biểu thức liên hợp.

+) Đặt nhân tử chung.

+) Rút gọn các phân thức trước khi tiến hành tính toán.

Lời giải chi tiết:

Biểu thức P có nghĩa khi và chỉ khi : \(\left\{ \begin{array}{l}\sqrt x  > 0\\\sqrt {x - 1}  \ge 0\\\sqrt 2  - \sqrt x  \ne 0\\\sqrt {x - 1}  - \sqrt 2  \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 0\\x \ge 1\\x \ne 2\\x \ne 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\x \ne 2\\x \ne 3\end{array} \right.\)

ĐKXĐ: \(x \ge 1;x \ne 2;x \ne 3\)

  \(\begin{array}{l}P = \left( {\frac{1}{{\sqrt x  - \sqrt {x - 1} }} - \frac{{x - 3}}{{\sqrt {x - 1}  - \sqrt 2 }}} \right)\left( {\frac{2}{{\sqrt 2  - \sqrt x }} - \frac{{\sqrt x  + \sqrt 2 }}{{\sqrt {2x}  - x}}} \right)\\P = \left[ {\frac{{\left( {\sqrt x  + \sqrt {x - 1} } \right)}}{{\left( {\sqrt x  - \sqrt {x - 1} } \right)\left( {\sqrt x  + \sqrt {x - 1} } \right)}} - \frac{{\left( {x - 3} \right)\left( {\sqrt {x - 1}  + \sqrt 2 } \right)}}{{\left( {\sqrt {x - 1}  - \sqrt 2 } \right)\left( {\sqrt {x - 1}  + \sqrt 2 } \right)}}} \right]\left[ {\frac{2}{{\sqrt 2  - \sqrt x }} - \frac{{\sqrt x  + \sqrt 2 }}{{\sqrt x \left( {\sqrt 2  - \sqrt x } \right)}}} \right]\\P = \left[ {\frac{{\sqrt x  + \sqrt {x - 1} }}{{x - \left( {x - 1} \right)}} - \frac{{\left( {x - 3} \right)\left( {\sqrt {x - 1}  + \sqrt 2 } \right)}}{{\left( {x - 1} \right) - 2}}} \right].\frac{{2\sqrt x  - \sqrt x  - \sqrt 2 }}{{\sqrt x \left( {\sqrt 2  - \sqrt x } \right)}}\\P = \left( {\frac{{\sqrt x  + \sqrt {x - 1} }}{{x - x + 1}} - \frac{{\left( {x - 3} \right)\left( {\sqrt {x - 1}  + \sqrt 2 } \right)}}{{x - 3}}} \right).\frac{{ - \left( {\sqrt 2  - \sqrt x } \right)}}{{\sqrt x \left( {\sqrt 2  - \sqrt x } \right)}}\\P = \left( {\sqrt x  + \sqrt {x - 1}  - \sqrt {x - 1}  - \sqrt 2 } \right).\frac{{ - 1}}{{\sqrt x }} = \frac{{\left( {\sqrt x  - \sqrt 2 } \right).\left( { - 1} \right)}}{{\sqrt x }} = \frac{{\sqrt 2  - \sqrt x }}{{\sqrt x }}\end{array}\)

Ta có: \(x = 3 + 2\sqrt 2  = {\left( {\sqrt 2  + 1} \right)^2} \Rightarrow \sqrt x  = \sqrt {{{\left( {\sqrt 2  + 1} \right)}^2}}  = \left| {\sqrt 2  + 1} \right| = \sqrt 2  + 1\,\,\left( {Do\,\,\sqrt 2  + 1 > 0} \right)\)

Thay \(\sqrt x  = \sqrt 2  + 1\) vào biểu thức \(P = \frac{{\sqrt 2  - \sqrt x }}{{\sqrt x }}\), ta có: \(P = \frac{{\sqrt 2  - \sqrt 2  - 1}}{{\sqrt 2  + 1}} = \frac{{ - 1}}{{\sqrt 2  + 1}} =  - \sqrt 2  + 1\).

Vậy khi \(x = 3 + 2\sqrt 2 \) thì \(P =  - \sqrt 2  + 1\).

Phương pháp giải:

+) Bước 1: Tìm điều kiện xác định của P

+) Bước 2: Áp dụng hằng đẳng thức rồi rút gọn P.

+) Bước 3: Cho \(P < 7 - 4\sqrt 3 \) ( P đã rút gọn ở trên). Từ đó tìm giá trị của a thỏa mãn yêu cầu.

Lời giải chi tiết:

ĐKXĐ: \(\left\{ \begin{array}{l}a \ge 0\\1 - \sqrt a  \ne 0\end{array} \right. \Leftrightarrow a \ge 0,a \ne 1\)

\(\begin{array}{l}P = \left( {\frac{{1 - a\sqrt a }}{{1 - \sqrt a }} + \sqrt a } \right).\left( {\frac{{1 + a\sqrt a }}{{1 + \sqrt a }} - \sqrt a } \right)\\P = \left( {\frac{{\left( {1 - \sqrt a } \right).\left( {1 + \sqrt a  + a} \right)}}{{1 - \sqrt a }} + \sqrt a } \right).\left( {\frac{{\left( {1 + \sqrt a } \right).\left( {1 - \sqrt a  + a} \right)}}{{1 + \sqrt a }} - \sqrt a } \right)\\P = \left( {1 + \sqrt a  + a + \sqrt a } \right).\left( {1 - \sqrt a  + a - \sqrt a } \right) = {\left( {1 + \sqrt a } \right)^2}.{\left( {1 - \sqrt a } \right)^2} = {\left( {1 - a} \right)^2}\\P < 7 - 4\sqrt 3  \Leftrightarrow P < {\left( {2 - \sqrt 3 } \right)^2}\\ \Rightarrow {\left( {1 - a} \right)^2} < {\left( {2 - \sqrt 3 } \right)^2} \Leftrightarrow \left| {1 - a} \right| < \left| {2 - \sqrt 3 } \right| \Leftrightarrow \left| {a - 1} \right| < 2 - \sqrt 3 \\ \Leftrightarrow  - 2 + \sqrt 3  < 1 - a < 2 - \sqrt 3  \Leftrightarrow \sqrt 3  - 1 < a < 3 - \sqrt 3 \end{array}\)

Kết hợp với điều kiện ta được \(a \in \left( {\sqrt 3  - 1;3 - \sqrt 3 } \right)/\left\{ 1 \right\}\) .

Vậy \(a \in \left( {\sqrt 3  - 1;3 - \sqrt 3 } \right)/\left\{ 1 \right\}\).

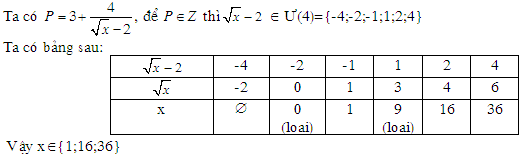
Phương pháp giải:

- Sử dụng biểu thức liên hợp.

- Rút gọn biểu thức.

Lời giải chi tiết:

ĐKXĐ: \(\left\{ \begin{array}{l}x \ge 0\\x \ne 1\end{array} \right.\)

\(\begin{array}{l}P = \left( {\frac{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  + 1} \right) - \left( {\sqrt x  - 1} \right)\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}} \right):\left( {\frac{{\sqrt x  - 1 + \sqrt x \left( {\sqrt x  + 1} \right) + 2}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}} \right)\\\,\,\,\,\, = \left( {\frac{{{{\left( {\sqrt x  + 1} \right)}^2} - {{\left( {\sqrt x  - 1} \right)}^2}}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}} \right).\left( {\frac{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}{{x + 2\sqrt x  + 1}}} \right)\\\,\,\,\,\, = \frac{{\left( {\sqrt x  + 1 - \sqrt x  + 1} \right)\left( {\sqrt x  + 1 + \sqrt x  - 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}.\frac{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}{{{{\left( {\sqrt x  + 1} \right)}^2}}}\\\,\,\,\,\, = \frac{{4\sqrt x }}{{{{\left( {\sqrt x  + 1} \right)}^2}}}\end{array}\)

Vậy \(P = \frac{{4\sqrt x }}{{{{\left( {\sqrt x  + 1} \right)}^2}}}\) (1)

a) Ta có \(x = \frac{{\sqrt {7 - 4\sqrt 3 } }}{2} = \frac{{\sqrt {{2^2} - 2.2.\sqrt 3  + {{\left( {\sqrt 3 } \right)}^2}} }}{2} = \frac{{\sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} }}{2} = \frac{{\left| {2 - \sqrt 3 } \right|}}{2} = \frac{{2 - \sqrt 3 }}{2}\,\,\left( {Do\,\,2 - \sqrt 3  > 0} \right)\)

\( \Rightarrow \sqrt x  = \sqrt {\frac{{2 - \sqrt 3 }}{2}}  = \frac{{\sqrt {4 - 2\sqrt 3 } }}{2} = \frac{{\sqrt {{{\left( {\sqrt 3  - 1} \right)}^2}} }}{2} = \frac{{\left| {\sqrt 3  - 1} \right|}}{2} = \frac{{\sqrt 3  - 1}}{2}\,\,\left( {Do\,\,\sqrt 3  - 1 > 0} \right)\)

Thay \(\sqrt x  = \frac{{\sqrt 3  - 1}}{2}\) vào  biểu thức P ta được:

\(P = \frac{{4\left( {\frac{{\sqrt 3  - 1}}{2}} \right)}}{{{{\left( {\frac{{\sqrt 3  - 1}}{2} + 1} \right)}^2}}} = \frac{{8\left( {\sqrt 3  - 1} \right)}}{{{{\left( {\sqrt 3  + 1} \right)}^2}}} = \frac{{8\left( {\sqrt 3  - 1} \right)}}{{4 + 2\sqrt 3 }} = \frac{{4\left( {\sqrt 3  - 1} \right)}}{{2 + \sqrt 3 }} = 4\left( {\sqrt 3  - 1} \right)\left( {2 - \sqrt 3 } \right) =  - 20 + 12\sqrt 3 \)

Vậy khi \(x = \frac{{\sqrt {7 - 4\sqrt 3 } }}{2}\) thì \(P = 20 - 12\sqrt 3 \).

b) Theo bài ra ta có \(P = \frac{1}{2} \Leftrightarrow \frac{{4\sqrt x }}{{{{\left( {\sqrt x  + 1} \right)}^2}}} = \frac{1}{2}\)

\(\begin{array}{l} \Leftrightarrow x + 2\sqrt x  + 1 = 8\sqrt x  \Leftrightarrow x - 6\sqrt x  + 1 = 0\\ \Leftrightarrow \left[ \begin{array}{l}\sqrt x  = 3 + 2\sqrt 2 \\\sqrt x  = 3 - 2\sqrt 2 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 17 + 12\sqrt 2 \\x = 17 - 12\sqrt 2 \end{array} \right.\,\,\left( {tm} \right)\end{array}\)

Vậy với \(x = 17 + 12\sqrt 2 \)hoặc \(x = 17 - 12\sqrt 2 \) thì \(P = \frac{1}{2}\).

Phương pháp giải:

a) Quy đồng, rút gọn.

b) Đưa biểu thức về dạng \(A\left( x \right) + \dfrac{C}{{B\left( x \right)}}\) với C là hằng số. Để biểu thức đó là số nguyên thì \(B\left( x \right) \in U\left( C \right)\).

c) Nhận xét mẫu số trước khi giải bất phương trình, lưu ý kết hợp điều kiện.

Lời giải chi tiết:

a) Với \(x \ge 0,x \ne 4,x \ne 9.\) Ta có:

\(\begin{array}{l}A = \left( {1 - \dfrac{{\sqrt x }}{{1 + \sqrt x }}} \right):\left( {\dfrac{{\sqrt x  + 3}}{{\sqrt x  - 2}} + \dfrac{{\sqrt x  + 2}}{{3 - \sqrt x }} + \dfrac{{\sqrt x  + 2}}{{x - 5\sqrt x  + 6}}} \right)\\A = \dfrac{1}{{\sqrt x  + 1}}:\left( {\dfrac{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}} - \dfrac{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}} + \dfrac{{\sqrt x  + 2}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}} \right)\\A = \dfrac{1}{{\sqrt x  + 1}}:\dfrac{{x - 9 - \left( {x - 4} \right) + \sqrt x  + 2}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}\\A = \dfrac{1}{{\sqrt x  + 1}}:\dfrac{{\sqrt x  - 3}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}} = \dfrac{{\sqrt x  - 2}}{{\sqrt x  + 1}}.\end{array}\)

b)  \(A = \dfrac{{\sqrt x  - 2}}{{\sqrt x  + 1}} = 1 - \dfrac{3}{{\sqrt x  + 1}}\left( {x \ge 0} \right)\)

Để \(A \in Z\) với x nguyên thì \(\sqrt x  + 1\) là ước nguyên dương của 3 do \(\sqrt x  + 1 > 0\)

.\( \Rightarrow \left[ \begin{array}{l}\sqrt x  + 1 = 1 \Leftrightarrow x = 0\,\,\,\left( {tm} \right)\\\sqrt x  + 1 = 3 \Leftrightarrow x = 4\,\,\left( {ktm} \right)\end{array} \right.\)

Vậy với \(x = 0\) thì \(A \in Z\)

c) \(A < 0 \Leftrightarrow \dfrac{{\sqrt x  - 2}}{{\sqrt x  + 1}} < 0.\)

Do \(\sqrt x  + 1 > 0 \Rightarrow \dfrac{{\sqrt x  - 2}}{{\sqrt x  + 1}} < 0 \Leftrightarrow \sqrt x  - 2 < 0 \Leftrightarrow x < 4.\)

Kết với \(x \ge 0\), suy ra \(A > 0 <  =  > 0 \le x < 4.\)

Vậy \(0 \le x < 4\) thì \(A < 0.\)

Phương pháp giải:

- Nhân liên hợp

- Quy đồng mẫu số

- Giải và biện luận phương trình

Lời giải chi tiết:

a) Ta có \(Q = \left( {\dfrac{1}{{\sqrt x  - 1}} + \dfrac{2}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}} \right):\left( {\dfrac{{\sqrt x \left( {\sqrt x  + 1} \right)}}{{\sqrt x  + 1}} - \dfrac{{1 - \sqrt x }}{{\sqrt x \left( {1 - \sqrt x } \right)}}} \right)\)

\(\begin{array}{l} = \dfrac{{\left( {\sqrt x  + 1} \right) + 2}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}:\left( {\sqrt x  - \dfrac{1}{{\sqrt x }}} \right)\\ = \dfrac{{\sqrt x  + 3}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}:\dfrac{{x - 1}}{{\sqrt x }}\\ = \dfrac{{\sqrt x  + 3}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}.\dfrac{{\sqrt x }}{{x - 1}}\\ = \dfrac{{\sqrt x \left( {\sqrt x  + 3} \right)}}{{{{\left( {x - 1} \right)}^2}.}}\end{array}\)

Vậy \(Q = \dfrac{{\sqrt x \left( {\sqrt x  + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}}\)

b. Ta thấy biểu thức \(Q = \dfrac{{\sqrt x \left( {\sqrt x  + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}}\)  luôn lớn hơn 0 với \(\forall x > 0,x \ne 1\)

\( \Rightarrow \)\(Q = \dfrac{{\sqrt x \left( {\sqrt x  + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}} =  - 1\) (vô lý)

Vậy không tồn tại giá trị nào của x để \(Q = \dfrac{{\sqrt x \left( {\sqrt x  + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}} =  - 1.\)

Phương pháp giải:

a) Sử dụng hằng đẳng thức, quy đồng, rút gọn biểu thức.

b) Giải phương trình \(P = 1\) , lưu ý ĐKXĐ.

Lời giải chi tiết:

a) Ta có

\(\begin{array}{l}P = \left( {1 - \dfrac{{\sqrt x \left( {\sqrt x  - 3} \right)}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}} \right):\left( {\dfrac{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right) + \left( {\sqrt x  - 2} \right)\left( {2 - \sqrt x } \right)}}{{\left( {2 - \sqrt x } \right)\left( {3 + \sqrt x } \right)}} - \dfrac{{9 - x}}{{x + \sqrt x  - 6}}} \right)\\P = \left( {1 - \dfrac{{\sqrt x }}{{\sqrt x  + 3}}} \right):\left( {\dfrac{{x - 9 - {{\left( {\sqrt x  - 2} \right)}^2}}}{{6 - \sqrt x  - x}} - \dfrac{{9 - x}}{{x + \sqrt x  - 6}}} \right)\\P = \dfrac{{\sqrt x  + 3 - \sqrt x }}{{\sqrt x  + 3}}:\left( {\dfrac{{x - 9 - \left( {x - 4\sqrt x  + 4} \right)}}{{6 - \sqrt x  - x}} - \dfrac{{9 - x}}{{x + \sqrt x  - 6}}} \right)\\P = \dfrac{3}{{\sqrt x  + 3}}:\left( {\dfrac{{13 - 4\sqrt x }}{{x + \sqrt x  - 6}} - \dfrac{{9 - x}}{{x + \sqrt x  - 6}}} \right)\\P = \dfrac{3}{{\sqrt x  + 3}}:\dfrac{{13 - 4\sqrt x  - 9 + x}}{{x + \sqrt x  - 6}}\\P = \dfrac{3}{{\sqrt x  + 3}}.\dfrac{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 2} \right)}}{{x - 4\sqrt x  + 4}}\\P = \dfrac{{3\left( {\sqrt x  - 2} \right)}}{{{{\left( {\sqrt x  - 2} \right)}^2}}} = \dfrac{3}{{\sqrt x  - 2}}\end{array}\)

b) Để \(P = 1 \Leftrightarrow \dfrac{3}{{\sqrt x  - 2}} = 1 \Leftrightarrow 3 = \sqrt x  - 2 \Leftrightarrow \sqrt x  = 5 \Leftrightarrow x = 25\,\,\left( {tm} \right)\)

Vậy với \(x = 25\) thì ta có giá trị của \(P = 1\)

Phương pháp giải:

Rút gọn những đơn thức đồng dạng.

Lời giải chi tiết:

\(M = \frac{{x{z^2}}}{{4xy}}.\frac{{20{x^2}}}{{{z^3}}} = \frac{{20{x^3}{z^2}}}{{4xy{z^3}}} = \frac{{5{x^2}}}{{yz}}\).

Chọn C.

Phương pháp giải:

Áp dụng công thức: \(\sqrt {{A^2}}  = \left[ \begin{array}{l}A\,\,\,khi\,\,\,\,A\,\,\, \ge 0\\ - A\,\,\,\,khi\,\,\,\,A < 0\end{array} \right..\)

Lời giải chi tiết:

Với \(x < 0\) thì \(N = \sqrt {{x^2}}  + \sqrt[3]{{{x^3}}} = \left| x \right| + x =  - x + x = 0.\)

Chọn B

Phương pháp giải:

Sử dụng định lí: Nếu đa thức : \(f\left( x \right) = ax + b\) có ít nhất 2 nghiệm thì \(a = b = 0\) tức là \(f\left( x \right) = 0\) với mọi x.

Lời giải chi tiết:

Đặt

\(\begin{array}{l}P(x) = \frac{{xb}}{{\left( {c + x} \right)\left( {c + b} \right)}} + \frac{{xc}}{{\left( {b + c} \right)\left( {b + x} \right)}} + \frac{{bc}}{{\left( {x + b} \right)\left( {x + c} \right)}} + \frac{{2xbc}}{{\left( {x + b} \right)\left( {x + c} \right)\left( {b + c} \right)}} - 1\\\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{xb\left( {x + b} \right) + xc\left( {x + c} \right) + bc\left( {b + c} \right) + 2xbc - \left( {x + b} \right)\left( {x + c} \right)\left( {b + c} \right)}}{{\left( {x + b} \right)\left( {x + c} \right)\left( {b + c} \right)}}\end{array}\)

Xét tử số \(f\left( x \right) = xb\left( {x + b} \right) + xc\left( {x + c} \right) + bc\left( {b + c} \right) + 2xbc - \left( {x + b} \right)\left( {x + c} \right)\left( {b + c} \right)\) có hệ số của \({x^2}\) là \(b + c - \left( {b + c} \right) = 0\) \( \Rightarrow \) Bậc của \(f\left( x \right)\) nhỏ hơn hoặc bằng 1.

Ta có : \(\left\{ \begin{array}{l}f\left( b \right) = {b^2}.2b + bc\left( {b + c} \right) + bc\left( {b + c} \right) + 2{b^2}c - 2b.{\left( {b + c} \right)^2} = 0\\f\left( c \right) = cb\left( {c + b} \right) + 2{c^3} + bc\left( {b + c} \right) + 2b{c^2} - 2c\left( {c + b} \right)\left( {b + c} \right) = 0\end{array} \right.\)

Do đó b, c là 2 nghiệm của phương trình \(f\left( x \right) = 0\).

Bậc của \(f\left( x \right)\) nhỏ hơn hoặc bằng 1, trong khi đó phương trình \(f\left( x \right) = 0\) lại có 2 nghiệm phân biệt \( \Leftrightarrow f\left( x \right) \equiv 0\,\,\forall x\) hay \(P\left( x \right) = 0\,\,\forall x\).

\(\begin{array}{l}P\left( x \right) = \frac{{xb}}{{\left( {c + x} \right)\left( {c + b} \right)}} + \frac{{xc}}{{\left( {b + c} \right)\left( {b + x} \right)}} + \frac{{bc}}{{\left( {x + b} \right)\left( {x + c} \right)}} + \frac{{2xbc}}{{\left( {x + b} \right)\left( {x + c} \right)\left( {b + c} \right)}} - 1\\P\left( x \right) = \frac{{xb\left( {x + b} \right) + xc\left( {x + c} \right) + bc\left( {b + c} \right) + 2xbc - \left( {x + b} \right)\left( {x + c} \right)\left( {b + c} \right)}}{{\left( {x + b} \right)\left( {x + c} \right)\left( {b + c} \right)}} = 0\\ \Rightarrow P\left( a \right) = \frac{{ab}}{{\left( {c + a} \right)\left( {c + b} \right)}} + \frac{{ac}}{{\left( {b + c} \right)\left( {b + a} \right)}} + \frac{{bc}}{{\left( {a + b} \right)\left( {a + c} \right)}} + \frac{{2abc}}{{\left( {a + b} \right)\left( {a + c} \right)\left( {b + c} \right)}} - 1 = 0\\ \Leftrightarrow \frac{{ab}}{{\left( {c + a} \right)\left( {c + b} \right)}} + \frac{{ac}}{{\left( {b + c} \right)\left( {b + a} \right)}} + \frac{{bc}}{{\left( {a + b} \right)\left( {a + c} \right)}} + \frac{{2abc}}{{\left( {a + b} \right)\left( {a + c} \right)\left( {b + c} \right)}} = 1\end{array}\)

Vậy \(\frac{{ab}}{{\left( {c + a} \right)\left( {c + b} \right)}} + \frac{{ac}}{{\left( {b + c} \right)\left( {b + a} \right)}} + \frac{{bc}}{{\left( {a + b} \right)\left( {a + c} \right)}} + \frac{{2abc}}{{\left( {a + b} \right)\left( {a + c} \right)\left( {b + c} \right)}} = 1\)

Phương pháp giải:

\(\frac{1}{{k\sqrt {k - 1}  + \left( {k - 1} \right)\sqrt k }} = \frac{1}{{\sqrt {k - 1} }} - \frac{1}{{\sqrt k }}\)

Lời giải chi tiết:

Ta có: \(k\sqrt {k - 1}  + \left( {k - 1} \right)\sqrt k \, = \sqrt {k\left( {k - 1} \right)} \left( {\sqrt k  + \sqrt {k - 1} } \right)\) với \(k \ge 1\).

\(\begin{array}{l} \Rightarrow \frac{1}{{k\sqrt {k - 1}  + \left( {k - 1} \right)\sqrt k }} = \frac{1}{{\sqrt {k\left( {k - 1} \right)} \left( {\sqrt k  + \sqrt {k - 1} } \right)}} = \frac{{\left( {\sqrt k  - \sqrt {k - 1} } \right)}}{{\sqrt {k\left( {k - 1} \right)} \left( {\sqrt k  + \sqrt {k - 1} } \right)\left( {\sqrt k  - \sqrt {k - 1} } \right)}}\\ = \frac{{\sqrt k  - \sqrt {k - 1} }}{{\sqrt {k\left( {k - 1} \right)} }} = \frac{{\sqrt k  - \sqrt {k - 1} }}{{\sqrt k .\sqrt {k - 1} }} = \frac{1}{{\sqrt {k - 1} }} - \frac{1}{{\sqrt k }}\end{array}\)  

Thay lại vào A ta được:

\(\begin{array}{l}A = \frac{1}{{2\sqrt 1  + 1\sqrt 2 }} + \frac{1}{{3\sqrt 2  + 2\sqrt 3 }} + ... + \frac{1}{{2018\sqrt {2017}  + 2017\sqrt {2018} }}\\\,\,\,\,\, = \,\left( {\frac{1}{{\sqrt 1 }} - \frac{1}{{\sqrt 2 }}} \right) + \left( {\frac{1}{{\sqrt 2 }} - \frac{1}{{\sqrt 3 }}} \right) + ..... + \left( {\frac{1}{{\sqrt {2017} }} - \frac{1}{{\sqrt {2018} }}} \right)\\\,\,\,\,\, = 1 - \frac{1}{{\sqrt {2018} }}\end{array}\)