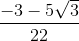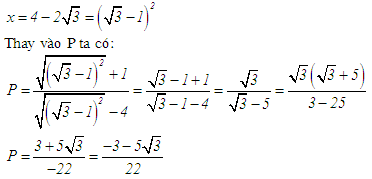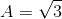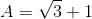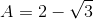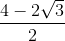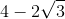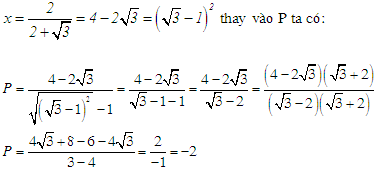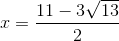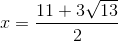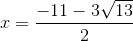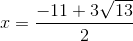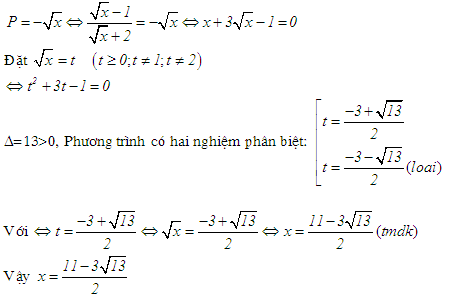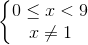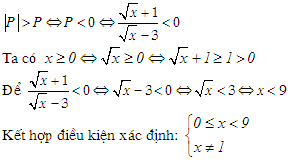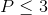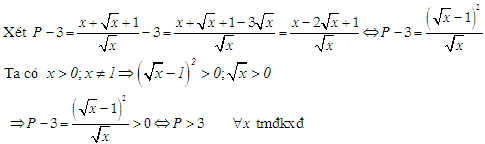Phương pháp giải:

Phương pháp:

+) Ta đưa biểu thức dưới dấu căn về dạng hằng đẳng thức \({{\left( A+B \right)}^{2}}\) hoặc \({{\left( A-B \right)}^{2}}\)  sau đó khai căn theo quy tắc: \(\sqrt{{{A}^{2}}}=\left| A \right|.\)

+) Trục căn thức ở mẫu để khử căn thức ở dưới mẫu sau đó rút gọn biểu thức.

 \(\frac{C}{A+\sqrt{B}}=\frac{C\left( A-\sqrt{B} \right)}{{{A}^{2}}-B};\,\,\,\frac{C}{A-\sqrt{B}}=\frac{C\left( A+\sqrt{B} \right)}{{{A}^{2}}-B}\) 

Lời giải chi tiết:

Giải:

\(\begin{array}{l}A = \sqrt {4 - 2\sqrt 3 } - \sqrt 3 \\\,\,\,\,\, = \sqrt {{{(\sqrt 3 - 1)}^2}} - \sqrt 3 \\\,\,\,\,\, = \sqrt 3 - 1 - \sqrt 3 \\\,\,\,\,\, = - 1.\end{array}\)

\(\begin{array}{l}B = \frac{4}{{3 - \sqrt 5 }} + \frac{4}{{3 + \sqrt 5 }}\\\,\,\,\, = \frac{{4\left( {3 + \sqrt 5 } \right)}}{{\left( {3 - \sqrt 5 } \right)\left( {3 + \sqrt 5 } \right)}} + \frac{{4\left( {3 - \sqrt 5 } \right)}}{{\left( {3 - \sqrt 5 } \right)\left( {3 + \sqrt 5 } \right)}}\\\,\,\,\,\, = \frac{{4\left( {3 + \sqrt 5 } \right)}}{{9 - 5}} + \frac{{4\left( {3 - \sqrt 5 } \right)}}{{9 - 5}}\\\,\,\,\,\, = 3 + \sqrt 5 + 3 - \sqrt 5 \\\,\,\,\,\, = 6.\end{array}\)

Phương pháp giải:

Lời giải chi tiết:

Phương pháp giải:

+) Tìm điều kiện xác định của biểu thức.

+) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức.

Lời giải chi tiết:

Điều kiện \(x \ge 0;x \ne 4\)

\(P = \left( {\frac{{3\sqrt x }}{{\sqrt x  + 2}} + \frac{{\sqrt x }}{{2 - \sqrt x }} + \frac{{8\sqrt x }}{{x - 4}}} \right):\left( {2 - \frac{{2\sqrt x  + 3}}{{\sqrt x  + 2}}} \right)\)

\(\begin{array}{l} = \left( {\frac{{3\sqrt x \left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}} - \frac{{\sqrt x \left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}} + \frac{{8\sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}} \right):\left( {\frac{{2\left( {\sqrt x  + 2} \right)}}{{\sqrt x  + 2}} - \frac{{2\sqrt x  + 3}}{{\sqrt x  + 2}}} \right)\\ = \frac{{3x - 6\sqrt x  - x - 2\sqrt x  + 8\sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}:\frac{{2\sqrt x  + 4 - 2\sqrt x  - 3}}{{\sqrt x  + 2}}\\ = \frac{{2x}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}.\left( {\sqrt x  + 2} \right) = \frac{{2x}}{{\sqrt x  - 2}}.\end{array}\)

Phương pháp giải:

+) Tìm điều kiện xác định của biểu thức.

+) Quy đồng mẫu các phân thức, biến đổi và rút gọn biểu thức.

+) Biến đổi \(x,\) thay giá trị \(x = \frac{8}{{3 + \sqrt 5 }}\,\,\,\left( {tm} \right)\) vào biểu thức \(P\) rồi tính giá trị biểu thức.

Lời giải chi tiết:

Điều kiện \(x \ge 0;x \ne 4\)

\(\begin{array}{l}P = \left( {\frac{{3\sqrt x }}{{\sqrt x  + 2}} + \frac{{\sqrt x }}{{2 - \sqrt x }} + \frac{{8\sqrt x }}{{x - 4}}} \right):\left( {2 - \frac{{2\sqrt x  + 3}}{{\sqrt x  + 2}}} \right)\\ = \left( {\frac{{3\sqrt x \left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}} - \frac{{\sqrt x \left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}} + \frac{{8\sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}} \right):\left( {\frac{{2\left( {\sqrt x  + 2} \right)}}{{\sqrt x  + 2}} - \frac{{2\sqrt x  + 3}}{{\sqrt x  + 2}}} \right)\\ = \frac{{3x - 6\sqrt x  - x - 2\sqrt x  + 8\sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}:\frac{{2\sqrt x  + 4 - 2\sqrt x  - 3}}{{\sqrt x  + 2}}\\ = \frac{{2x}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}.\left( {\sqrt x  + 2} \right) = \frac{{2x}}{{\sqrt x  - 2}}.\end{array}\)

Ta có : \(x = \frac{8}{{3 + \sqrt 5 }} = \frac{{8\left( {3 - \sqrt 5 } \right)}}{{{3^2} - 5}} = 2\left( {3 - \sqrt 5 } \right)\,\,\,\,\left( {tm} \right).\)

\( \Rightarrow \sqrt x  = \sqrt {2\left( {3 - \sqrt 5 } \right)}  = \sqrt {6 - 2\sqrt 5 }  = \sqrt {{{\left( {\sqrt 5  - 1} \right)}^2}}  = \left| {\sqrt 5  - 1} \right| = \sqrt 5  - 1.\)  

Khi đó ta có:  \(P = \frac{{2.\left( {6 - 2\sqrt 5 } \right)}}{{\sqrt 5  - 1 - 2}} = \frac{{2.\left( {6 - 2\sqrt 5 } \right)\left( {\sqrt 5  + 3} \right)}}{{ - 4}} =  - 4.\)

Phương pháp giải:

Bình luận về bài toán:

Đây là một câu thuộc dạng “cho điểm” những học sinh có học lực từ trung bình.

Các em lưu ý về bài rút gọn căn thức dạng phân số: Nếu ta không thể nhóm nhân tử chung của tử số để rút gọn phân số thì phương pháp hữu hiệu nhất là “liên hợp”. Liên hợp là phương pháp có sức mạnh rất lớn trong việc giải quyết bài toán rút gọn biểu thức chứa phân số.

Liên hợp là cách thức ta nhân cả tử và mẫu với cùng một biểu thức để mẫu số cho ra dạng hằng đẳng thức số 3:  \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\)

Lời giải chi tiết:

\(\eqalign{& A = {4 \over {\sqrt 3  - 1}} - {{\sqrt {15}  + \sqrt 3 } \over {\sqrt 5  + 1}} - 3\sqrt {{1 \over 3}}   \cr  & \,\,\,\, = {{4.\left( {\sqrt 3  + 1} \right)} \over {\left( {\sqrt 3  - 1} \right)\left( {\sqrt 3  + 1} \right)}} - {{\sqrt 3 .\left( {\sqrt 5  + 1} \right)} \over {\sqrt 5  + 1}} - 3{{\sqrt 1 } \over {\sqrt 3 }}  \cr & \,\,\,\, = {{4.\left( {\sqrt 3  + 1} \right)} \over 2} - \sqrt 3  - \sqrt 3   \cr  & \,\,\,\, = 2.\left( {\sqrt 3  + 1} \right) - 2\sqrt 3   \cr & \,\,\,\, = 2\sqrt 3  + 2 - 2\sqrt 3   \cr & \,\,\,\, = 2 \cr} \)

Phương pháp giải:

Bình luận về bài toán:

Đây là dạng bài tập rút gọn biểu thức chứa chữ. Dạng bài tập này những năm gần đây không xuất hiện. Tuy nhiên, điều  đó không có nghĩa là sẽ không thi và chúng ta chủ quan bỏ qua. Trong đề thi minh họa năm vừa rồi dạng bài này vẫn có một bài. Trong tình hình thi cử năm nay, chúng ta không nên suy đoán chủ quan và “học tủ”. Những dạng toán cơ bản, mà nhiều khi chúng ta bỏ qua thì cơ hội năm nay thi sẽ rất cao. Những dạng toán truyền thống thì ngược lại sẽ không nhiều nữa. Có rất nhiều em, bài tập khó thì làm được, bài tập dễ thì không biêt làm, hoặc làm sai, trình bày không được. Các em vốn quen học theo kiểu được “luyện gà chọi”  nên cái gì “lạ lạ” mà gặp phải là lúng túng không làm được.

Để làm dạng bài tập này, trước hết nếu đề chưa cho điều kiện thì các em phải tìm điều kiện cho biểu thức xác định. Cụ thể:

\(\sqrt{A}\)  xác định \(\Leftrightarrow A\ge 0\). Nếu có dạng:  \(\dfrac{f(x)}{\sqrt{A}}\)  xác định \(\Leftrightarrow A>0\)

\(\dfrac{A}{B}\)  xác định \(\Leftrightarrow B\ne 0\)

Sau khi tìm điều kiện xong (nếu đề chưa cho điều kiện), các em sẽ tìm mẫu số chung của biểu thức rồi tiến hành quy đồng và thực hiện các phép tính. Nếu có có biểu thức trong ngoặc thì tiến hành rút gọn biểu thức trong ngoặc trước.

Lời giải chi tiết:

\(\begin{array}{l}A = \left( {\dfrac{1}{{\sqrt x - 1}} - \dfrac{{\sqrt x }}{{1 - x}}} \right).\dfrac{{x - \sqrt x }}{{2\sqrt x + 1}}\\A = \left( {\dfrac{1}{{\sqrt x - 1}} + \dfrac{{\sqrt x }}{{x - 1}}} \right).\dfrac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{2\sqrt x + 1}}\\A = \left( {\dfrac{1}{{\sqrt x - 1}} + \dfrac{{\sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right).\dfrac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{2\sqrt x + 1}}\\A = \left( {\dfrac{{\sqrt x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} + \dfrac{{\sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right).\dfrac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{2\sqrt x + 1}}\\A = \left( {\dfrac{{\sqrt x + 1 + \sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right).\dfrac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{2\sqrt x + 1}}\\A = \left( {\dfrac{{2\sqrt x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right).\dfrac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{2\sqrt x + 1}}\\A = \dfrac{{\sqrt x }}{{\sqrt x + 1}}\end{array}\)

Phương pháp giải:

Rút gọn biểu phân thức 

Lời giải chi tiết:

Vì \(a \ge 0,\)  ta có \(P = \sqrt {\frac{{5a}}{{32}}} .\sqrt {\frac{{2a}}{5}}  = \sqrt {\frac{{5a.2a}}{{32.5}}}  = \sqrt {\frac{{{a^2}}}{{16}}}  = \frac{{\left| a \right|}}{4} = \frac{a}{4}.\)

Chọn đáp án B

Phương pháp giải:

Trục căn thức ở mẫu hoặc quy đồng mẫu các phân thức để tính giá trị của biểu thức.

Lời giải chi tiết:

\(E = \frac{1}{{\sqrt 2  - 1}} - \frac{1}{{\sqrt 2  + 1}} = \frac{{\sqrt 2  + 1 - \sqrt 2  + 1}}{{\left( {\sqrt 2  - 1} \right)\left( {\sqrt 2  + 1} \right)}} = \frac{2}{{2 - 1}} = 2.\)

Chọn C.

Phương pháp giải:

Phân tích tử và mẫu thành nhân tử rồi rút gọn.

Lời giải chi tiết:

\(\begin{array}{l}T = \dfrac{{\left( {\sqrt {2a}  - 2\sqrt 2 } \right)\left( {a - 1} \right)}}{{a - \sqrt a  - 2}}\,\,\,\,\left( {a > 0;a \ne 4} \right)\\ = \dfrac{{\sqrt 2 \left( {\sqrt a  - 2} \right)\left( {\sqrt a  - 1} \right)\left( {\sqrt a  + 1} \right)}}{{\left( {\sqrt a  - 2} \right)\left( {\sqrt a  + 1} \right)}}\\ = \sqrt 2 \left( {\sqrt a  - 1} \right)\end{array}\)

Vậy \(T = \sqrt 2 \left( {\sqrt a  - 1} \right)\).

Phương pháp giải:

Lời giải chi tiết:

Phương pháp giải:

Lời giải chi tiết:

Phương pháp giải:

Lời giải chi tiết:

Phương pháp giải:

Lời giải chi tiết:

Phương pháp giải:

Lời giải chi tiết:

Phương pháp giải:

Lời giải chi tiết:

a) Hàm số xác định \(  \Leftrightarrow \left\{ \matrix{ x \ge 0 \hfill \cr  x - 1 \ge 0 \hfill \cr \sqrt x  + \sqrt {x - 1}  \ne 0 \hfill \cr  \sqrt x  - \sqrt {x - 1}  \ne 0 \hfill \cr 1 - \sqrt x  \ne 0 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{x \ge 0 \hfill \cr x \ge 1 \hfill \cr \forall x \ge 1 \hfill \cr  \sqrt x  \ne \sqrt {x - 1}  \hfill \cr \sqrt x  \ne 1 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{ x \ge 1 \hfill \cr x \ne x - 1 \hfill \cr  x \ne 1 \hfill \cr}  \right. \Leftrightarrow x > 1.  \)

b) Ta có:  \( \left( {\sqrt x  + \sqrt {x - 1} } \right)\left( {\sqrt x  - \sqrt {x - 1} } \right) = {\left( {\sqrt x } \right)^2} - {\left( {\sqrt {x - 1} } \right)^2} = x - \left( {x - 1} \right) = 1.\)

\( \eqalign{& C = {1 \over {\sqrt x  + \sqrt {x - 1} }} - {1 \over {\sqrt x  - \sqrt {x - 1} }} - {{x\sqrt x  - x} \over {1 - \sqrt x }}  \cr & \,\,\,\,\, = {{\sqrt x  - \sqrt {x - 1}  - \left( {\sqrt x  + \sqrt {x - 1} } \right)} \over {\left( {\sqrt x  + \sqrt {x - 1} } \right)\left( {\sqrt x  - \sqrt {x - 1} } \right)}} - {{x\left( {\sqrt x  - 1} \right)} \over {1 - \sqrt x }}  \cr & \,\,\,\,\, = {{\sqrt x  - \sqrt {x - 1}  - \sqrt x  - \sqrt {x - 1} } \over 1} + x\, = x - 2\sqrt {x - 1} . \cr} \)

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

\( \eqalign{ & D = \left( {{{\sqrt x  + \sqrt y } \over {1 - \sqrt {xy} }} - {{\sqrt x  - \sqrt y } \over {1 + \sqrt {xy} }}} \right):\left( {{{y + xy} \over {1 - xy}}} \right)  \cr & \,\,\,\,\, = {{\left( {\sqrt x  + \sqrt y } \right)\left( {1 + \sqrt {xy} } \right) - \left( {\sqrt x  - \sqrt y } \right)\left( {1 - \sqrt {xy} } \right)} \over {\left( {1 - \sqrt {xy} } \right)\left( {1 + \sqrt {xy} } \right)}}.{{1 - xy} \over {y + xy}}  \cr  & \,\,\,\,\, = {{\sqrt x  + \sqrt y  + x\sqrt y  + y\sqrt x  - \left( {\sqrt x  - \sqrt y  - x\sqrt y  + y\sqrt x } \right)} \over {1 - xy}}.{{1 - xy} \over {y + xy}}  \cr  & \,\,\,\,\, = {{\sqrt x  + \sqrt y  + x\sqrt y  + y\sqrt x  - \sqrt x  + \sqrt y  + x\sqrt y  - y\sqrt x } \over {y + xy}}  \cr  & \,\,\,\,\, = {{2\sqrt y  + 2x\sqrt y } \over {y + xy}} = {{2\sqrt y \left( {x + 1} \right)} \over {y\left( {x + 1} \right)}} = {2 \over {\sqrt y }}. \cr} \)

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

\( \eqalign{ & M = \left( {{{x\sqrt x } \over {\sqrt x  + 1}} + {{{x^2}} \over {x\sqrt x  + x}}} \right)\left( {2 - {1 \over {\sqrt x }}} \right) = \left( {{{x\sqrt x } \over {\sqrt x  + 1}} + {x \over {\sqrt x  + 1}}} \right){{2\sqrt x  - 1} \over {\sqrt x }}  \cr  & \,\,\,\,\,\, = {{x\left( {\sqrt x  + 1} \right)} \over {\sqrt x  + 1}}.{{2\sqrt x  - 1} \over {\sqrt x }} = \sqrt x \left( {2\sqrt x  - 1} \right) = 2x - \sqrt x . \cr}  \)

Chọn B.

Phương pháp giải:

Lời giải chi tiết:

\(  \eqalign{ & N = \left( {{1 \over {\sqrt x  - 3}} - {1 \over {\sqrt x }}} \right):\left( {{{\sqrt x  + 3} \over {\sqrt x  - 2}} - {{\sqrt x  + 2} \over {\sqrt x  - 3}}} \right)  \cr & \,\,\,\,\, = {{\sqrt x  - \sqrt x  + 3} \over {\sqrt x \left( {\sqrt x  - 3} \right)}}:{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right) - \left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)} \over {\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}  \cr  & \,\,\,\,\,\, = {3 \over {\sqrt x \left( {\sqrt x  - 3} \right)}}:{{x - 9 - x + 4} \over {\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)}}  \cr  & \,\,\,\,\,\, = {3 \over {\sqrt x \left( {\sqrt x  - 3} \right)}}.{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 3} \right)} \over { - 5}}\, = {{ - 3\left( {\sqrt x  - 2} \right)} \over {5\sqrt x }} = {{6 - 3\sqrt x } \over {5\sqrt x }}. \cr} \)

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

\( \eqalign{& P = \left( {{{\sqrt a } \over {\sqrt a  - 1}} - {1 \over {a - \sqrt a }}} \right):\left( {{1 \over {\sqrt a  + 1}} + {2 \over {a - 1}}} \right)  \cr & \,\,\,\,\, = \left( {{{\sqrt a } \over {\sqrt a  - 1}} - {1 \over {\sqrt a \left( {\sqrt a  - 1} \right)}}} \right):\left( {{1 \over {\sqrt a  + 1}} + {2 \over {\left( {\sqrt a  + 1} \right)\left( {\sqrt a  - 1} \right)}}} \right)  \cr & \,\,\,\,\, = {{a - 1} \over {\sqrt a \left( {\sqrt a  - 1} \right)}}:{{\sqrt a  - 1 + 2} \over {\left( {\sqrt a  + 1} \right)\left( {\sqrt a  - 1} \right)}}  \cr  & \,\,\,\,\, = {{\sqrt a  + 1} \over {\sqrt a }}.{{\left( {\sqrt a  + 1} \right)\left( {\sqrt a  - 1} \right)} \over {\sqrt a  + 1}}  \cr & \,\,\,\,\, = {{a - 1} \over {\sqrt a }}. \cr}  \)

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

a) Hàm số xác định \(  \Leftrightarrow \left\{ \matrix{x \ge 0 \hfill \cr \sqrt x  - 1 \ne 0 \hfill \cr  \sqrt x  - 3 \ne 0 \hfill \cr 1 - {1 \over {\sqrt x  - 1}} \ne 0 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{x \ge 0 \hfill \cr \sqrt x  \ne 1 \hfill \cr \sqrt x  \ne 3 \hfill \cr  {1 \over {\sqrt x  - 1}} \ne 1 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{x \ge 0 \hfill \cr x \ne 1 \hfill \cr x \ne 9 \hfill \cr \sqrt x  - 1 \ne 1 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{x \ge 0 \hfill \cr x \ne 1 \hfill \cr x \ne 9 \hfill \cr  \sqrt x  \ne 2 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{x \ge 0 \hfill \cr  x \ne 1 \hfill \cr x \ne 4 \hfill \cr x \ne 9 \hfill \cr}  \right..  \)

\( \eqalign{& b)\,B = \left( {{{\sqrt x  + 2} \over {\sqrt x  - 1}} - {{\sqrt x  + 1} \over {\sqrt x  - 3}} + {{3\sqrt x  - 1} \over {\left( {\sqrt x  - 1} \right)\left( {\sqrt x  - 3} \right)}}} \right):\left( {1 - {1 \over {\sqrt x  - 1}}} \right)  \cr  & \,\,\,\,\,\,\,\,\,\,\, = {{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 3} \right) - \left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right) + 3\sqrt x  - 1} \over {\left( {\sqrt x  - 1} \right)\left( {\sqrt x  - 3} \right)}}:{{\sqrt x  - 1 - 1} \over {\sqrt x  - 1}}  \cr & \,\,\,\,\,\,\,\,\,\,\, = {{x - \sqrt x  - 6 - x + 1 + 3\sqrt x  - 1} \over {\left( {\sqrt x  - 1} \right)\left( {\sqrt x  - 3} \right)}}.{{\sqrt x  - 1} \over {\sqrt x  - 2}}  \cr & \,\,\,\,\,\,\,\,\,\,\, = {{2\sqrt x  - 6} \over {\left( {\sqrt x  - 3} \right)\left( {\sqrt x  - 2} \right)}} = {{2\left( {\sqrt x  - 3} \right)} \over {\left( {\sqrt x  - 3} \right)\left( {\sqrt x  - 2} \right)}} = {2 \over {\sqrt x  - 2}}. \cr}   \)

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

\( \eqalign{ & P = {{{a^2} + \sqrt a } \over {a - \sqrt a  + 1}} - {{2a + \sqrt a } \over {\sqrt a }} + 1  \cr & \,\,\,\, = {{\sqrt a \left( {a\sqrt a  + 1} \right)} \over {a - \sqrt a  + 1}} - {{\sqrt a \left( {2\sqrt a  + 1} \right)} \over {\sqrt a }} + 1  \cr & \,\,\,\, = {{\sqrt a \left( {\sqrt a  + 1} \right)\left( {a - \sqrt a  + 1} \right)} \over {a - \sqrt a  + 1}} - \left( {2\sqrt a  + 1} \right) + 1  \cr & \,\,\,\, = \sqrt a \left( {\sqrt a  + 1} \right) - 2\sqrt a  - 1 + 1  \cr & \,\,\,\, = a + \sqrt a  - 2\sqrt a   \cr & \,\,\,\, = a - \sqrt a . \cr}  \)

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

a) Hàm số xác định \( \Leftrightarrow \left\{ \matrix{x \ge 0 \hfill \cr \sqrt x  + 3 \ne 0 \hfill \cr 3 - \sqrt x  \ne 0 \hfill \cr x - 9 \ne 0 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{x \ge 0 \hfill \cr  \forall x \ge 0 \hfill \cr  x \ne 9 \hfill \cr x \ne 9 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{x \ge 0 \hfill \cr  x \ne 9 \hfill \cr}  \right..\)

\( \eqalign{& b)\,A = {{2\sqrt x } \over {\sqrt x  + 3}} - {{\sqrt x  - 1} \over {3 - \sqrt x }} - {{3 - 11\sqrt x } \over {x - 9}}  \cr & \,\,\,\,\,\,\,\,\,\,\,\, = {{2\sqrt x } \over {\sqrt x  + 3}} + {{\sqrt x  - 1} \over {\sqrt x  - 3}} - {{3 - 11\sqrt x } \over {\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}  \cr & \,\,\,\,\,\,\,\,\,\,\,\, = {{2\sqrt x \left( {\sqrt x  - 3} \right) + \left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right) - 3 + 11\sqrt x } \over {\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}  \cr  & \,\,\,\,\,\,\,\,\,\,\,\, = {{2x - 6\sqrt x  + x + 2\sqrt x  - 3 - 3 + 11\sqrt x } \over {\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}  \cr & \,\,\,\,\,\,\,\,\,\,\,\, = \,{{3x + 7\sqrt x  - 6} \over {\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}  \cr & \,\,\,\,\,\,\,\,\,\,\,\, = {{\left( {3\sqrt x  - 2} \right)\left( {\sqrt x  + 3} \right)} \over {\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}} = {{3\sqrt x  - 2} \over {\sqrt x  - 3}}. \cr}  \)

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

a) Biếu thức P xác định  \(  \Leftrightarrow \left\{ \matrix{x \ge 0 \hfill \cr \sqrt x  - 2 \ne 0 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{x \ge 0 \hfill \cr  \sqrt x  \ne 2 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{x \ge 0 \hfill \cr x \ne 4 \hfill \cr}  \right..\)

Biểu thức Q xác định \(  \Leftrightarrow \left\{ \matrix{ x \ge 0 \hfill \cr \sqrt x  + 2 \ne 0 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{x \ge 0 \hfill \cr \forall x \ge 0 \hfill \cr}  \right. \Leftrightarrow x \ge 0. \)

b) Ta có:

\( \eqalign{& P = {{2x - 3\sqrt x  - 2} \over {\sqrt x  - 2}} = {{\left( {\sqrt x  - 2} \right)\left( {2\sqrt x  + 1} \right)} \over {\sqrt x  - 2}} = 2\sqrt x  + 1.  \cr & Q = {{\sqrt {{x^3}}  - \sqrt x  + 2x - 2} \over {\sqrt x  + 2}} = {{\sqrt x \left( {x - 1} \right) + 2\left( {x - 1} \right)} \over {\sqrt x  + 2}}  \cr & \,\,\,\,\, = {{\left( {\sqrt x  + 2} \right)\left( {x - 1} \right)} \over {\sqrt x  + 2}} = x - 1. \cr} \)

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

a) Biểu thức xác định \( \Leftrightarrow \left\{ \matrix{x \ge 0 \hfill \cr \sqrt x  \ne 0 \hfill \cr x - \sqrt x  \ne 0 \hfill \cr  x + \sqrt x  \ne 0 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{ x \ge 0 \hfill \cr x \ne 0 \hfill \cr \sqrt x \left( {\sqrt x  - 1} \right) \ne 0 \hfill \cr \sqrt x \left( {\sqrt x  + 1} \right) \ne 0 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{ x > 0 \hfill \cr  \sqrt x  - 1 \ne 0 \hfill \cr \forall x \ge 0 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{ x > 0 \hfill \cr  x \ne 1 \hfill \cr}  \right.. \)

\(  \eqalign{& b)\,P = {{2x + 2} \over {\sqrt x }} + {{x\sqrt x  - 1} \over {x - \sqrt x }} - {{x\sqrt x  + 1} \over {x + \sqrt x }}  \cr & \,\,\,\,\,\,\,\,\,\,\, = {{2x + 2} \over {\sqrt x }} + {{\left( {\sqrt x  - 1} \right)\left( {x + \sqrt x  + 1} \right)} \over {\sqrt x \left( {\sqrt x  - 1} \right)}} - {{\left( {\sqrt x  + 1} \right)\left( {x - \sqrt x  + 1} \right)} \over {\sqrt x \left( {\sqrt x  + 1} \right)}}  \cr& \,\,\,\,\,\,\,\,\,\,\, = {{2x + 2} \over {\sqrt x }} + {{x + \sqrt x  + 1} \over {\sqrt x }} - {{x - \sqrt x  + 1} \over {\sqrt x }}  \cr & \,\,\,\,\,\,\,\,\,\,\, = {{2x + 2 + x + \sqrt x  + 1 - x + \sqrt x  - 1} \over {\sqrt x }}  \cr & \,\,\,\,\,\,\,\,\,\,\, = {{2x + 2\sqrt x  + 2} \over {\sqrt x }}. \cr}  \)

Chọn B.

Phương pháp giải:

Lời giải chi tiết:

\( \eqalign{& P = \left( {{{3x + \sqrt {9x}  - 3} \over {x + \sqrt x  - 2}} + {1 \over {\sqrt x  - 1}} + {1 \over {\sqrt x  + 2}}} \right):{1 \over {x - 1}}  \cr & \,\,\,\, = \left( {{{3x + 3\sqrt x  - 3} \over {\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}} + {1 \over {\sqrt x  - 1}} + {1 \over {\sqrt x  + 2}}} \right):{1 \over {x - 1}}  \cr & \,\,\,\, = {{3x + 3\sqrt x  - 3 + \sqrt x  + 2 + \sqrt x  - 1} \over {\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}.\left( {x - 1} \right)  \cr & \,\,\,\, = {{3x + 5\sqrt x  - 2} \over {\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}.\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)  \cr & \,\,\,\, = {{\left( {3\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)} \over {\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 2} \right)}}  \cr & \,\,\,\, = \left( {3\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right). \cr}  \)

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

\(\begin{array}{l}B = \frac{1}{{\sqrt x  + 1}} - \frac{{x + 2}}{{x\sqrt x  + 1}} = \frac{1}{{\sqrt x  + 1}} - \frac{{x + 2}}{{\left( {\sqrt x  + 1} \right)\left( {x - \sqrt x  + 1} \right)}}\\ = \frac{{x - \sqrt x  + 1 - x - 2}}{{\left( {\sqrt x  + 1} \right)\left( {x - \sqrt x  + 1} \right)}} = \frac{{ - \sqrt x  - 1}}{{\left( {\sqrt x  + 1} \right)\left( {x - \sqrt x  + 1} \right)}}\\ = \frac{{ - \left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {x - \sqrt x  + 1} \right)}} = \frac{{ - 1}}{{x - \sqrt x  + 1}}\end{array}\)

Phương pháp giải:

a) Sử dụng biểu thức liên hợp.

b) Sử dụng biểu thức liên hợp.

Lời giải chi tiết:

\(\begin{array}{l}a)\,\,A = \frac{1}{{\sqrt 5  - 1}} + \frac{1}{{\sqrt 5  + 1}} = \frac{{\sqrt 5  + 1}}{{(\sqrt 5  - 1)(\sqrt 5  + 1)}} + \frac{{\sqrt 5  - 1}}{{\left( {\sqrt 5  + 1} \right)\left( {\sqrt 5  - 1} \right)}}\\\,\,\,\,\,A = \frac{{\sqrt 5  + 1}}{4} + \frac{{\sqrt 5  - 1}}{4} = \frac{{\sqrt 5 }}{2}\\b)\,\,B = \frac{1}{{\sqrt 1  + \sqrt 2 }} + \frac{1}{{\sqrt 2  + \sqrt 3 }} + ... + \frac{1}{{\sqrt {99}  + \sqrt {100} }}\\\,\,\,\,\,B = \frac{1}{{\sqrt 2  + \sqrt 1 }} + \frac{1}{{\sqrt 3  + \sqrt 2 }} + ... + \frac{1}{{\sqrt {100}  + \sqrt {99} }}\\\,\,\,\,\,B = \frac{{\sqrt 2  - \sqrt 1 }}{{2 - 1}} + \frac{{\sqrt 3  - \sqrt 2 }}{{3 - 2}} + \frac{{\sqrt 4  - \sqrt 3 }}{{4 - 3}}... + \frac{{\sqrt {100}  - \sqrt {99} }}{{100 - 99}}\\\,\,\,\,\,B =  - \sqrt 1  + \sqrt {100}  =  - 1 + 10 = 9\end{array}\)

Phương pháp giải:

Quy đồng và rút gọn biểu thức.

Lời giải chi tiết:

ĐK: \(\left\{ \begin{array}{l}x \ge 0\\\sqrt x  - 1 \ne 0\\\sqrt x  + 3 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\x \ne 1\\x \ne 9\end{array} \right.\,\,\left( * \right)\)

Với đk (*) ta có:

\(\begin{array}{l}P = \frac{{x\sqrt x  + 26\sqrt x  - 19}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right)}} - \frac{{2\sqrt x }}{{\sqrt x  - 1}} + \frac{{\sqrt x  - 3}}{{\sqrt x  + 3}}\\P = \frac{{x\sqrt x  + 26\sqrt x  - 19 - 2\sqrt x \left( {\sqrt x  + 3} \right) + \left( {\sqrt x  - 3} \right)\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right)}}\\P = \frac{{x\sqrt x  + 26\sqrt x  - 19 - 2x - 6\sqrt x  + x - 4\sqrt x  + 3}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right)}}\\P = \frac{{x\sqrt x  - x + 16\sqrt x  - 16}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right)}}\\P = \frac{{x\left( {\sqrt x  - 1} \right) + 16\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right)}}\\P = \frac{{\left( {x + 16} \right)\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 3} \right)}} = \frac{{x + 16}}{{\sqrt x  + 3}}\end{array}\)

Vậy \(P = \frac{{x + 16}}{{\sqrt x  + 3}}\)

Phương pháp giải:

Quy đồng và rút gọn.

Lời giải chi tiết:

ĐKXĐ : \(x \ge 0;y \ge 0;xy \ne 1\).

\(\begin{array}{l}P = \left( {\frac{{\sqrt x  + \sqrt y }}{{1 - \sqrt {xy} }} + \frac{{\sqrt x  - \sqrt y }}{{1 + \sqrt {xy} }}} \right):\left( {1 + \frac{{x + y + 2xy}}{{1 - xy}}} \right)\\P = \frac{{\left( {\sqrt x  + \sqrt y } \right)\left( {1 + \sqrt {xy} } \right) + \left( {\sqrt x  - \sqrt y } \right)\left( {1 - \sqrt {xy} } \right)}}{{1 - xy}}:\frac{{1 - xy + x + y + 2xy}}{{1 - xy}}\\P = \frac{{\sqrt x  + x\sqrt y  + \sqrt y  + y\sqrt x  + \sqrt x  - x\sqrt y  - \sqrt y  + y\sqrt x }}{{1 - xy}}.\frac{{1 - xy}}{{1 + x + y + xy}}\\P = \frac{{2\left( {\sqrt x  + y\sqrt x } \right)}}{{\left( {1 + x} \right)\left( {1 + y} \right)}} = \frac{{2\sqrt x \left( {1 + y} \right)}}{{\left( {1 + x} \right)\left( {1 + y} \right)}} = \frac{{2\sqrt x }}{{1 + x}}\end{array}\)

Phương pháp giải:

Quy đồng và rút gọn biểu thức.

Lời giải chi tiết:

\(\begin{array}{l}P = \left( {\frac{{\sqrt x  + 1}}{{\sqrt x  - 1}} + \frac{{\sqrt x }}{{2 + \sqrt x }} - \frac{{4x + 2\sqrt x  - 4}}{{x - 4}}} \right)\left( {\frac{2}{{2 - \sqrt x }} - \frac{{\sqrt x  + 3}}{{2\sqrt x  - x}}} \right)\\P = \frac{{\left( {\sqrt x  + 1} \right)\left( {x - 4} \right) + \sqrt x \left( {\sqrt x  - 1} \right)\left( {\sqrt x  - 2} \right) - \left( {4x + 2\sqrt x  - 4} \right)\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}.\frac{{2\sqrt x  - \left( {\sqrt x  + 3} \right)}}{{\sqrt x \left( {2 - \sqrt x } \right)}}\\P = \frac{{\left( {x\sqrt x  + x - 4\sqrt x  - 4} \right) + \left( {x\sqrt x  - 3x + 2\sqrt x } \right) - \left( {4x\sqrt x  - 2x - 6\sqrt x  + 4} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}.\frac{{\sqrt x  - 3}}{{\sqrt x \left( {2 - \sqrt x } \right)}}\\P = \frac{{ - 2x\sqrt x  + 4\sqrt x  - 8}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}.\frac{{\sqrt x  - 3}}{{\sqrt x \left( {2 - \sqrt x } \right)}}\\P = \frac{{ - 2.\left( {x\sqrt x  + 8 - 2\sqrt x  - 4} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}.\frac{{\sqrt x  - 3}}{{\sqrt x \left( {2 - \sqrt x } \right)}}\\P = \frac{{ - 2.\left[ {\left( {\sqrt x  + 2} \right)\left( {x - 2\sqrt x  + 4} \right) - 2\left( {\sqrt x  + 2} \right)} \right]}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}.\frac{{\sqrt x  - 3}}{{\sqrt x \left( {2 - \sqrt x } \right)}}\\P = \frac{{2\left( {\sqrt x  + 2} \right)\left( {x - 2\sqrt x  + 2} \right)\left( {\sqrt x  - 3} \right)}}{{\sqrt x \left( {\sqrt x  - 1} \right){{\left( {\sqrt x  - 2} \right)}^2}\left( {\sqrt x  + 2} \right)}}\\P = \frac{{2\left( {x - 2\sqrt x  + 2} \right)\left( {\sqrt x  - 3} \right)}}{{\sqrt x \left( {\sqrt x  - 1} \right){{\left( {\sqrt x  - 2} \right)}^2}}}\end{array}\)