40 bài tập trắc nghiệm một số phương trình lượng giác thường gặp mức độ nhận biết, thông hiểuLàm bàiQuảng cáo
Câu hỏi 1 : Trong các phương trình sau phương trình nào có nghiệm ?
Đáp án: D Phương pháp giải: Xét các điều kiện có nghiệm của từng hàm số. Lời giải chi tiết: +) phương trình \(\sqrt 3 \sin \left( {3x - \dfrac{\pi }{3}} \right) - 3 = 0 \Leftrightarrow \sin \left( {3x - \dfrac{\pi }{3}} \right) = \sqrt 3 > 1\) (Loại). +) Phương trình \(\sin 3x + \sqrt 3 {\rm{cos}}3x = - 4\) có nghiệm khi \({1^2} + 3 \ge {\left( { - 4} \right)^2}\)(vô lí). +)Phương trình \(2\cos 3x + 3 = 0 \Leftrightarrow cos3x = - \dfrac{3}{2} < - 1\) (Loại). Chọn D Câu hỏi 2 : Cho phương trình \(3{\cos ^2}x + 2\cos x - 5 = 0\). Nghiệm của phương trình là :
Đáp án: B Phương pháp giải: Giải phương trình bậc hai rồi tìm nghiệm. Lời giải chi tiết: \(\begin{array}{l}3{\cos ^2}x + 2\cos x - 5 = 0 \Leftrightarrow \left( {3\cos x + 5} \right)\left( {\cos x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\cos x = 1\\\cos x = - \dfrac{5}{3}\,\,\left( {loai} \right)\end{array} \right. \Leftrightarrow x = k2\pi \,\,\left( {k \in \mathbb{Z}} \right).\end{array}\) Chọn A. Câu hỏi 3 : Điều kiện cần và đủ để phương trình \(a\sin x + b\cos x = c\) có nghiệm là:
Đáp án: D Phương pháp giải: + Phương trình \(a\sin x + b\cos x = c\) có nghiệm khi \({a^2} + {b^2} \ge {c^2}.\) + Phương trình \(a\sin x + b\cos x = c\) có nghiệm khi \({a^2} + {b^2} < {c^2}.\) Lời giải chi tiết: Phương trình \(a\sin x + b\cos x = c\) có nghiệm khi \({a^2} + {b^2} \ge {c^2}.\) Chọn D. Câu hỏi 4 : Có bao nhiêu số nguyên \(m\) để phương trình \(12\sin x - 5\cos x = m\) có nghiệm.
Đáp án: D Phương pháp giải: Phương trình \(a\sin x + b\cos x = c\) có nghiệm \( \Leftrightarrow {a^2} + {b^2} \ge {c^2}\). Lời giải chi tiết: Phương trình \(12\sin x - 5\cos x = m\) có nghiệm \( \Leftrightarrow {12^2} + {5^2} \ge {m^2} \Leftrightarrow {m^2} \le 169 \Leftrightarrow - 13 \le m \le 13\). Vậy có \(27\) số nguyên \(m\) thỏa mãn yêu cầu bài toán. Chọn D. Câu hỏi 5 : Giải phương trình : \(2\sin x + \sqrt 3 = 0.\)
Đáp án: A Phương pháp giải: Lời giải chi tiết: Ta có : \(2\sin x = \sqrt 3 \Leftrightarrow \sin x = - \dfrac{{\sqrt 3 }}{2} \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{\pi }{3} + k2\pi \\x = \pi + \dfrac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{\pi }{3} + k2\pi \\x = \dfrac{{4\pi }}{3} + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right).\) Vậy phương trình đã cho có nghiệm: \(x = - \dfrac{\pi }{3} + k2\pi ;\,\,x = \dfrac{{4\pi }}{3} + k2\pi \,\left( {k \in \mathbb{Z}} \right).\) Câu hỏi 6 : Nghiệm của phương trình \(\sqrt 3 \tan x - 1 = 0\) là:
Đáp án: B Phương pháp giải: Giải phương trình lượng giác cơ bản: \(\tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\). Lời giải chi tiết: \(\sqrt 3 \tan x - 1 = 0 \Leftrightarrow \tan x = \dfrac{1}{{\sqrt 3 }} \Leftrightarrow x = \dfrac{\pi }{6} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\). Chọn B. Câu hỏi 7 : Phương trình \(\sin x + \sqrt 3 \cos x = 0\) có nghiệm dương nhỏ nhất là:
Đáp án: D Phương pháp giải: \(a\sin x+b\cos x=0\Leftrightarrow a\sin x=-b\cos x\Leftrightarrow \tan x=-\dfrac{b}{a}\) Lời giải chi tiết: \(\sin x+\sqrt{3}\cos x=0\Leftrightarrow \sin x=-\sqrt{3}\cos x\Leftrightarrow \tan x=-\sqrt{3}\Leftrightarrow x=-\dfrac{\pi }{3}+k\pi \,\,\left( k\in \mathbb{Z} \right)\). \(x > 0 \Leftrightarrow - \dfrac{\pi }{3} + k\pi > 0 \Leftrightarrow k > \dfrac{1}{3}\,\,\left( {k \in \mathbb{Z}} \right)\). Ta có \(x=-\dfrac{\pi }{3}+k\pi \Rightarrow {{x}_{\min }}\Leftrightarrow {{k}_{\min }}\,\,\left( k\in \mathbb{Z} \right)\Leftrightarrow k=1\). Vậy nghiệm dương nhỏ nhất của phương trình là \(x=-\dfrac{\pi }{3}+\pi =\dfrac{2\pi }{3}\). Chọn D. Câu hỏi 8 : Phương trình \(\sqrt 3 \cos x - \sin x = 0\) có nghiệm là:
Đáp án: B Phương pháp giải: \(a\sin x+b\cos x=0\Leftrightarrow a\sin x=-b\cos x\Leftrightarrow \tan x=-\dfrac{b}{a}\). Lời giải chi tiết: \(\sqrt 3 \cos x - \sin x = 0\). + Chia cả 2 vế cho \(\sqrt{{{\left( -1 \right)}^{2}}+{{\left( \sqrt{3} \right)}^{2}}}=2\). + Phương trình \(\Leftrightarrow \sin x=\sqrt{3}\cos x\Leftrightarrow \tan x=\sqrt{3}\Leftrightarrow x=\dfrac{\pi }{3}+k\pi \,\,\left( k\in \mathbb{Z} \right)\). Chọn B. Câu hỏi 9 : Nghiệm của phương trình \(\sin x + \cos x = 1\) là:
Đáp án: C Phương pháp giải: Phương trình dạng \(a\sin x + b\cos x = c\). Chia cả 2 vế của phương trình cho \(\sqrt{{{a}^{2}}+{{b}^{2}}}\). Lời giải chi tiết: \(\sin x+\cos x=1\Leftrightarrow \sqrt{2}\sin \left( x+\dfrac{\pi }{4} \right)=1\Leftrightarrow \sin \left( x+\dfrac{\pi }{4} \right)=\dfrac{1}{\sqrt{2}}\) \( \Leftrightarrow \left[ \matrix{ Chọn C. Câu hỏi 10 : Nghiệm của phương trình \(2{\tan ^2}x + 5\tan x + 3 = 0\) là:
Đáp án: A Phương pháp giải: Giải phương trình bậc hai tìm \(\tan x\) sau đó giải phương trình lượng giác cơ bản. Lời giải chi tiết: \(\begin{array}{l}2{\tan ^2}x + 5\tan x + 3 = 0\,\,\left( {a - b + c = 0} \right)\\ \Leftrightarrow \left[ \begin{array}{l}\tan x = - 1\\\tan x = - \dfrac{3}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{\pi }{4} + k\pi \\x = \arctan \left( { - \dfrac{3}{2}} \right) + k\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\) Chọn A Câu hỏi 11 : Phương trình \({\cos ^2}2x + \cos 2x - \dfrac{3}{4} = 0\) có nghiệm là:
Đáp án: C Phương pháp giải: Giải phương trình bậc hai tìm \(\cos 2x\) sau đó giải phương trình lượng giác cơ bản. Lời giải chi tiết: \(\begin{array}{l}{\cos ^2}2x + \cos 2x - \dfrac{3}{4} = 0 \Leftrightarrow 4{\cos ^2}2x + 4\cos 2x - 3 = 0\\ \Leftrightarrow \left[ \begin{array}{l}\cos 2x = - \dfrac{3}{2}\,\,\left( {loai} \right)\\\cos 2x = \dfrac{1}{2}\,\,\,\left( {tm} \right)\end{array} \right. \Leftrightarrow 2x = \pm \dfrac{\pi }{3} + k2\pi \Leftrightarrow x = \pm \dfrac{\pi }{6} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\end{array}\) Chọn C Câu hỏi 12 : Phương trình \(2{\sin ^2}x + \sin x - 3 = 0\) có nghiệm là:
Đáp án: D Phương pháp giải: Sử dụng công thức nhẩm nghiệm \(\left( {a + b + c = 0} \right)\) sau đó giải phương trình lượng giác cơ bản. Lời giải chi tiết: \(\begin{array}{l}2{\sin ^2}x + \sin x - 3 = 0\,\,\left( {a + b + c = 0} \right)\\ \Leftrightarrow \left[ \begin{array}{l}\sin x = 1\,\,\,\,\,\,\,\,\left( {tm} \right)\\\sin x = - \dfrac{3}{2}\,\,\left( {loai} \right)\end{array} \right. \Leftrightarrow x = \dfrac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\end{array}\). Chọn D Câu hỏi 13 : Tất cả các nghiệm của phương trình \(\cos 2x - 5\cos x + 3 = 0\).
Đáp án: B Phương pháp giải: Sử dụng công thức nhân đôi \(\cos 2x = 2{\cos ^2}x - 1\). Lời giải chi tiết: \(\begin{array}{l}\cos 2x - 5\cos x + 3 = 0 \Leftrightarrow 2{\cos ^2}x - 1 - 5\cos x + 3 = 0\\ \Leftrightarrow 2{\cos ^2}x - 5\cos x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}\cos x = 2\,\,\left( {loai} \right)\\\cos x = \dfrac{1}{2}\,\,\,\left( {tm} \right)\end{array} \right. \Leftrightarrow x = \pm \dfrac{\pi }{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\end{array}\) Chọn B Câu hỏi 14 : Phương trình \(\sqrt 3 \sin x - \cos x = 1\) tương đương với phương trình nào sau đây:
Đáp án: A Phương pháp giải: Phương trình dạng \(a\sin x+b\cos x=c\). Chia cả 2 vế của phương trình cho \(\sqrt {{a^2} + {b^2}} \). Lời giải chi tiết: \(\sqrt{3}\sin x-\cos x=1\). + Chia cả 2 vế cho \(\sqrt{{{\left( \sqrt{3} \right)}^{2}}+{{\left( -1 \right)}^{2}}}=2\). + Phương trình \(\Leftrightarrow \dfrac{\sqrt{3}}{2}\sin x-\dfrac{1}{2}\cos x=\dfrac{1}{2}\Leftrightarrow \sin x\cos \dfrac{\pi }{6}-\cos x\sin \dfrac{\pi }{6}=\dfrac{1}{2}\Leftrightarrow \sin \left( x-\dfrac{\pi }{6} \right)=\dfrac{1}{2}\). Chọn A. Câu hỏi 15 : Giải phương trình \(\sqrt 3 \sin 2x + \cos 2x = 2\cos x\).
Đáp án: A Phương pháp giải: Phương trình dạng \(a\sin x + b\cos x = c\). Chia cả 2 vế cho \(\sqrt {{a^2} + {b^2}} \). Lời giải chi tiết: Ta có: \(\begin{array}{l}\,\,\,\,\,\sqrt 3 \sin 2x + \cos 2x = 2\cos x \Leftrightarrow \dfrac{{\sqrt 3 }}{2}\sin 2x + \dfrac{1}{2}\cos 2x = \cos x\\ \Leftrightarrow \sin \dfrac{\pi }{3}.\sin 2x + \cos \dfrac{\pi }{3}.\cos 2x = \cos x\\ \Leftrightarrow \cos \left( {2x - \dfrac{\pi }{3}} \right) = \cos x \Leftrightarrow \left[ \begin{array}{l}2x - \dfrac{\pi }{3} = x + k2\pi \\2x - \dfrac{\pi }{3} = - x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{3} + k2\pi \\x = \dfrac{\pi }{9} + k\dfrac{{2\pi }}{3}\end{array} \right.\,\,\left( {k \in Z} \right)\end{array}\) Vậy, phương trình đã cho có nghiệm \(x = \dfrac{\pi }{3} + k2\pi ,\,\,x = \dfrac{\pi }{9} + k\dfrac{{2\pi }}{3};\,\,k \in Z\). Câu hỏi 16 : Phương trình \({\sin ^2}x = 1\) tương đương với phương trình nào sau đây?
Đáp án: D Phương pháp giải: Sử dụng công thức nhân đôi: \(\cos 2x = 1 - 2{\sin ^2}x\). Lời giải chi tiết: Ta có: \({\sin ^2}x = 1 \Leftrightarrow \cos 2x = 1 - 2{\sin ^2}x = 1 - 2.1 = - 1\). Chọn: D Câu hỏi 17 : Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(\sqrt 3 \cos x + m - 1 = 0\) có nghiệm?
Đáp án: C Phương pháp giải: +) Quy về dạng \(\cos (f(x)) = f(m) \Rightarrow - 1 \le f(m) \le 1\) +) Giải điều kiện tìm m. Lời giải chi tiết: Ta có \(\sqrt 3 \cos x + m - 1 = 0 \Leftrightarrow \cos x = \frac{{1 - m}}{{\sqrt 3 }}\). Phương trình có nghiệm \( \Leftrightarrow - 1 \le \frac{{1 - m}}{{\sqrt 3 }} \le 1\) \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}1 - m \ge - \sqrt 3 \\1 - m \le \sqrt 3 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 1 + \sqrt 3 \\m \ge 1 - \sqrt 3 \end{array} \right.\\ \Leftrightarrow 1 - \sqrt 3 \le m \le 1 + \sqrt 3 \,\,\,\left( {m \in Z} \right) \Rightarrow m \in \left\{ {0;1;2} \right\}.\end{array}\) Vậy có tất cả 3 giá trị nguyên của tham số \(m\). Chọn C Câu hỏi 18 : Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) để phương trình \({\rm{cos}}\left( {2x - \frac{\pi }{3}} \right) - m = 2\) có nghiệm. Tính tổng \(T\) của các phần tử trong \(S\).
Đáp án: D Phương pháp giải: +) Quy về dạng \(\cos (f(x)) = f(m) \Rightarrow - 1 \le f(m) \le 1\) +) Giải điều kiện tìm m. +) Tính tổng. Lời giải chi tiết: Phương trình \({\rm{cos}}\left( {2x - \frac{\pi }{3}} \right) - m = 2 \Leftrightarrow {\rm{cos}}\left( {2x - \frac{\pi }{3}} \right) = m + 2\). Phương trình có nghiệm \( \Leftrightarrow - 1 \le m + 2 \le 1 \Leftrightarrow - 3 \le m \le - 1\). Mà \(m \in Z \Rightarrow S = \left\{ { - 3; - 2; - 1} \right\} \Rightarrow T = \left( { - 3} \right) + \left( { - 2} \right) + \left( { - 1} \right) = - 6\). Chọn D Câu hỏi 19 : Cho phương trình: \(\cos 2x + \sin x - 1 = 0\;\;\left( * \right).\) Bằng cách đặt \(t = \sin x\;\;\left( { - 1 \le t \le 1} \right)\) thì phương trình \(\left( * \right)\)trở thành phương trình nào sau đây?
Đáp án: A Phương pháp giải: Sử dụng công thức : \(\cos 2x = 1 - 2{\sin ^2}x\) Đặt \(\sin x = t\) quy về phương trình bậc 2 ẩn t. Lời giải chi tiết: \(\cos 2x + \sin x - 1 = 0 \Leftrightarrow 1 - 2{\sin ^2}x + \sin x - 1 = 0 \Leftrightarrow - 2{\sin ^2}x + \sin x = 0\;\;\left( * \right)\) Đặt \(\sin x = t \Rightarrow \left( * \right) \Leftrightarrow - 2{t^2} + t = 0\) Chọn A Câu hỏi 20 : Nghiệm của phương trình \({\sin ^2}x = -\sin x + 2\) là:
Đáp án: A Phương pháp giải: Đặt \(t = \sin x\) quy về phương trình bậc 2 ẩn t. Lời giải chi tiết: Đặt \(t = \sin x\). Điều kiện \(\left| t \right| \le 1\) Phương trình trở thành: \({t^2} = - t + 2 \Leftrightarrow {t^2} + t - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1{\rm{ (tm)}}\\t = - 2{\rm{ (ktm)}}\end{array} \right..\) Với \(t = 1 \Rightarrow \sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi {\rm{ (k}} \in {\rm{Z)}}{\rm{.}}\) Chọn A Câu hỏi 21 : Với giá trị nào của \(m\) thì phương trình \(\sin {\mkern 1mu} x - m = 1\) có nghiệm là:
Đáp án: D Phương pháp giải: +) Quy về dạng \(\sin \,x = f(m) \Rightarrow - 1 \le f(m) \le 1\) +) Giải điều kiện tìm m. Lời giải chi tiết: Ta có \(\sin \,x - m = 1 \Leftrightarrow \sin x = m + 1\;\;\left( * \right)\) Vì \( - 1 \le \sin x \le 1 \Rightarrow \) phương trình (*) có nghiệm \( \Leftrightarrow - 1 \le m + 1 \le 1 \Leftrightarrow - 2 \le m \le 0\). Vậy để phương trình đã cho có nghiệm thì \( - 2 \le m \le 0.\) Chọn D Câu hỏi 22 : Tìm số nghiệm của phương trình \(\sin 3x = \cos 2x\) thuộc \(\left[ {0;10\pi } \right]\)?
Đáp án: A Phương pháp giải: +) Giải phương trình bằng công thức nghiệm. +) Từ công thức nghiệm tìm số nguyên k để tìm nghiệm thỏa mãn bài toán. Lời giải chi tiết: \(\sin 3x = \cos 2x \Leftrightarrow \sin 3x = \sin \left( {\frac{\pi }{2} - 2x} \right) \Leftrightarrow \left[ \begin{array}{l}3x = \frac{\pi }{2} - 2x + k2\pi \\3x = \pi - \left( {\frac{\pi }{2} - 2x} \right) + m2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{10}} + \frac{{k2\pi }}{5}\\x = \frac{\pi }{2} + m2\pi \end{array} \right.\,\,\,\left( {k,\;m \in \mathbb{Z}} \right).\) Phương trình có nghiệm thuộc \(\left[ {0;\;10\pi } \right]\) \( \Leftrightarrow \left[ \begin{array}{l}0 \le \frac{\pi }{{10}} + \frac{{k2\pi }}{5} \le 10\pi \Leftrightarrow - \frac{1}{4} \le k \le \frac{{99}}{4} = 24\frac{3}{4} \Leftrightarrow k \in \left\{ {0;\;1;\;2;...;\;24} \right\}\\0 \le \frac{\pi }{2} + m2\pi \le 10\pi \Leftrightarrow - \frac{1}{4} \le k \le \frac{{19}}{4} = 4\frac{3}{4} \Leftrightarrow m \in \left\{ {0;\;1;...;\;4} \right\}\end{array} \right.\) Phương trình có \(25 + 5 = 30\) nghiệm thỏa mãn. Chọn A. Câu hỏi 23 : Nghiệm dương nhỏ nhất của phương trình \(\sin x+\sqrt{3}\cos x=\sqrt{2}\) là:
Đáp án: D Phương pháp giải: Áp dụng phương pháp giải phương trình bậc nhất đối với sin và cos \(a\sin x+b\cos x=c\) bằng cách chia cả 2 vế cho \(\sqrt{{{a}^{2}}+{{b}^{2}}}\). Lời giải chi tiết: \(\begin{array}{l}\sin x + \sqrt 3 \cos x = \sqrt 2 \Leftrightarrow \frac{1}{2}\sin x + \frac{{\sqrt 3 }}{2}\cos x = \frac{{\sqrt 2 }}{2} \Leftrightarrow \sin x\cos \frac{\pi }{3} + \cos x\sin \frac{\pi }{3} = \frac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sin \left( {x + \frac{\pi }{3}} \right) = \frac{{\sqrt 2 }}{2} \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{3} = \frac{\pi }{4} + k2\pi \\x + \frac{\pi }{3} = \frac{{3\pi }}{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \frac{\pi }{{12}} + k2\pi \\x = \frac{{5\pi }}{{12}} + k2\pi \end{array} \right.\,\,\left( {k \in Z} \right)\end{array}\) Vậy nghiệm dương nhỏ nhất của phương trình trên là \(x = \frac{{5\pi }}{{12}}.\) Chọn D. Câu hỏi 24 : Với giá trị nào của m thì phương trình \(\sin x+\cos x=m\) có nghiệm:
Đáp án: D Phương pháp giải: Phương trình bậc nhất đối với sin và cos: \(a\sin x+b\cos x=c\) có nghiệm khi và chỉ khi \({{a}^{2}}+{{b}^{2}}\ge {{c}^{2}}\) Lời giải chi tiết: Phương trình có nghiệm khi và chỉ khi \({{1}^{2}}+{{1}^{2}}\ge {{m}^{2}}\Leftrightarrow -\sqrt{2}\le m\le \sqrt{2}\) Chọn D. Câu hỏi 25 : Phương trình \({\rm{co}}{{\rm{s}}^2}x - {\sin ^2}x = 1\) có bao nhiêu nghiệm thuộc đoạn \(\left[ {0;\pi } \right]\)?
Đáp án: A Phương pháp giải: - Sử dụng công thức: \({\rm{co}}{{\rm{s}}^2}x - {\sin ^2}x = {\rm{cos}}\,{\rm{2}}x.\) - Giải phương trình lượng giác đặc biệt: \(\cos \alpha = 1 \Leftrightarrow \alpha = k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\). Lời giải chi tiết: Ta có: \(\begin{array}{l}{\rm{co}}{{\rm{s}}^2}x - {\sin ^2}x = 1 \Leftrightarrow {\rm{cos}}\,{\rm{2}}x = 1\\ \Leftrightarrow 2x = k2\pi ,\,\,k \in \mathbb{Z} \Leftrightarrow x = k\pi ,\,\,k \in \mathbb{Z}\end{array}\) Mà \(x \in \left[ {0;\pi } \right] \Rightarrow x \in \left\{ {0;\pi } \right\}\). Vậy phương trình có 2 nghiệm thỏa mãn. Chọn A. Câu hỏi 26 : Nghiệm của phương trình \(\cos \left( {x - \dfrac{\pi }{3}} \right) - \sqrt 3 \sin \left( {x - \dfrac{\pi }{3}} \right) = 1\) là.
Đáp án: A Phương pháp giải: Phương pháp giải phương trình lượng giác: \(a\sin x + b\cos x = c\). - Chia cả 2 vế của phương trình cho \(\sqrt {{a^2} + {b^2}} \). - Sử dụng công thức \(\sin a\cos b \pm \cos a\sin b = \sin \left( {a \pm b} \right)\), \(\cos a\cos b \pm \sin a\sin b = \cos \left( {a \mp b} \right)\) đưa phương trình về phương trình lượng giác cơ bản: \(\sin x = \sin \alpha \) hoặc \(\cos x = \cos \alpha \). - Giải phương trình lượng giác cơ bản: \(\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\) hoặc \(\cos x = \cos \alpha \Leftrightarrow x = \pm \alpha + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\). Lời giải chi tiết: TXĐ: \(D = \mathbb{R}\). \(\begin{array}{l}\,\,\,\,\,\,\cos \left( {x - \dfrac{\pi }{3}} \right) - \sqrt 3 \sin \left( {x - \dfrac{\pi }{3}} \right) = 1\\ \Leftrightarrow \dfrac{1}{2}.\cos \left( {x - \dfrac{\pi }{3}} \right) - \dfrac{{\sqrt 3 }}{2}\sin \left( {x - \dfrac{\pi }{3}} \right) = \dfrac{1}{2}\\ \Leftrightarrow \cos \dfrac{\pi }{3}.\cos \left( {x - \dfrac{\pi }{3}} \right) - \sin \dfrac{\pi }{3}.\sin \left( {x - \dfrac{\pi }{3}} \right) = \dfrac{1}{2}\\ \Leftrightarrow \cos \left( {x - \dfrac{\pi }{3} + \dfrac{\pi }{3}} \right) = \cos \dfrac{\pi }{3}\\ \Leftrightarrow \cos x = \cos \dfrac{\pi }{3} \Leftrightarrow x = \pm \dfrac{\pi }{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\end{array}\) Chọn A. Câu hỏi 27 : Tập tất cả các giá trị của m để phương trình \(5\sin \,x - 12{\rm{cos}}\,x = m\) có nghiệm là:
Đáp án: A Phương pháp giải: Phương trình \(a\sin \,x + b\,{\rm{cos}}\,x = c\) có nghiệm \( \Leftrightarrow {a^2} + {b^2} \ge {c^2}.\) Lời giải chi tiết: Phương trình \(5\sin \,x - 12{\rm{cos}}\,x = m\) có nghiệm \( \Leftrightarrow {5^2} + {12^2} \ge {m^2} \Leftrightarrow \)\( - 13 \le m \le 13\). Chọn A. Câu hỏi 28 : Nghiệm của phương trình \(\sqrt 3 \sin x - \cos x = 2\) là:
Đáp án: A Phương pháp giải: Giải phương trình lượng giác có dạng \(a\sin x + b\cos x = c\). - Chia cả 2 vế của phương trình cho \(\sqrt {{a^2} + {b^2}} \). - Sử dụng công thức \(\sin \left( {a \pm b} \right) = \sin a\cos b \pm \cos a\sin b\) đưa về phương trình lượng giác cơ bản \(\sin \alpha = \sin m\). - Giải phương trình lượng giác cơ bản: \(\sin \alpha = \sin m \Leftrightarrow \left[ \begin{array}{l}\alpha = m + k2\pi \\\alpha = \pi - m + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\). Lời giải chi tiết: \(\begin{array}{l}\,\,\,\,\,\,\sqrt 3 \sin x - \cos x{\rm{ = 2}}\\ \Leftrightarrow \dfrac{{\sqrt 3 }}{2}\sin x - \dfrac{1}{2}\cos x{\rm{ = 1}}\\ \Leftrightarrow \cos \dfrac{\pi }{6}.\sin x - \sin \dfrac{\pi }{6}.\cos x = 1\\ \Leftrightarrow \sin \left( {x - \dfrac{\pi }{6}} \right) = 1\\ \Leftrightarrow x - \dfrac{\pi }{6} = \dfrac{\pi }{2} + k2\pi \\ \Leftrightarrow x = \dfrac{{2\pi }}{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\end{array}\) Chọn A. Câu hỏi 29 : Phương trình \(3{\tan ^2}x + \left( {6 - \sqrt 3 } \right)\tan x - 2\sqrt 3 = 0\) có nghiệm là :
Đáp án: C Phương pháp giải: Giải phương trình bậc 2 rồi tìm nghiệm. Lời giải chi tiết: Ta có \(3{\tan ^2}x + \left( {6 - \sqrt 3 } \right)\tan x - 2\sqrt 3 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}\tan x = \dfrac{{\sqrt 3 }}{3}\\\tan x = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k\pi \\x = \arctan \left( { - 2} \right) + k\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\) Chọn C. Câu hỏi 30 : Cho phương trình \(m{\sin ^2}x + 2\sin x\cos x + 3m{\cos ^2}x = 1\). Có bao nhiêu giá trị nguyên thuộc khoảng \(\left( {0;2019} \right)\) của tham số \(m\) để phương trình vô nghiệm.
Đáp án: A Phương pháp giải: - TH1: \(\cos x = 0\). - TH2: \(\cos x \ne 0\): Giải phương trình bậc hai đối với \(\sin x,\,\,\cos x\) bằng cách chia cả hai vế cho \({\cos ^2}x\), đưa phương trình về phương trình bậc hai đối với \(\tan x\). - Điều kiện để phương trình bậc hai vô nghiệm là \(\Delta < 0\) hoặc \(\Delta ' < 0\). Lời giải chi tiết: Xét phương trình \(m{\sin ^2}x + 2\sin x\cos x + 3m{\cos ^2}x = 1\) (*) TH1: \(\cos x = 0\), phương trình trở thành: \(m = 1\) (luôn đúng). Khi đó phương trình luôn có nghiệm \(x = \dfrac{\pi }{2} + k\pi \,\,\left( {\,k \in \mathbb{Z}} \right)\) khi \(m = 1\).Loại \(m = 1.\) TH2: \(\cos x \ne 0\). Phương trình không có nghiệm \(x = \dfrac{\pi }{2} + k\pi \,\,\left( {\,k \in \mathbb{Z}} \right)\) Chia cả hai vế của phương trình (*) cho \({\cos ^2}x\) ta được: \(\begin{array}{l}\,\,\,\,\,\,\,m{\tan ^2}x + 2\tan \,x + 3m = 1 + {\tan ^2}x\\ \Leftrightarrow \left( {m - 1} \right){\tan ^2}x + 2\tan \,x + 3m - 1 = 0\,\,\left( {**} \right)\end{array}\) Phương trình (**) vô nghiệm \( \Leftrightarrow \left\{ \begin{array}{l}m - 1 \ne 0\\\Delta ' = 1 - \left( {m - 1} \right)\left( {3m - 1} \right) < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 1\\ - 3{m^2} + 4m < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 1\\\left[ \begin{array}{l}m > \dfrac{4}{3}\\m < 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m > \dfrac{4}{3}\\m < 0\end{array} \right.\) Kết hợp 2 trường hợp ta có: \(m \in \left( { - \infty ;0} \right) \cup \left( {\dfrac{4}{3}; + \infty } \right)\). Mà \(m \in \mathbb{Z},\,\,m \in \left( {0;2019} \right)\)\( \Rightarrow m \in \left\{ {2;3;4;...;2018} \right\}\). Vậy có 2017 giá trị của \(m\) thỏa mãn yêu cầu bài toán. Chọn: A. Câu hỏi 31 : \({\sin ^2}x - 3\sin x\cos x = - 1.\)
Đáp án: B Phương pháp giải: Lời giải chi tiết: \({\sin ^2}x - 3\sin x.\cos x = - 1\) +Xét \(\cos x = 0 \Rightarrow {\sin ^2}x = - 1(L)\) +Xét \(\cos x \ne 0\). Chia 2 vế cho \({\cos ^2}x\) \(\begin{array}{l} \Rightarrow {\tan ^2}x - 3\tan x = \frac{{ - 1}}{{{{\cos }^2}x}} = - 1\left( {1 + {{\tan }^2}x} \right)\\ \Leftrightarrow \left[ \begin{array}{l}\tan x = \frac{1}{2}\\\tan x = 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + k\pi \\x = \arctan \frac{1}{2} + k\pi \end{array} \right.\,\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\) Chọn B. Câu hỏi 32 : \({\sin ^2}x + 2{\cos ^2}x = 3\sin x\cos x.\)
Đáp án: C Phương pháp giải: Lời giải chi tiết: \({\sin ^2}x + 2{\cos ^2}x = 3\sin x.\cos x\) +Xét \(\cos x = 0 \Rightarrow {\sin ^2}x = 0 \Rightarrow x = 0\) +Xét \(\cos x \ne 0\). Chia 2 vế cho \({\cos ^2}x\) \(\begin{array}{l} \Rightarrow {\tan ^2}x + 2 - 3\tan x = 0\\ \Leftrightarrow \left[ \begin{array}{l}\tan x = 2\\\tan x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \arctan 2 + k\pi \\x = \frac{\pi }{4} + k\pi \end{array} \right.\,\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\) Chọn C. Câu hỏi 33 : Giải phương trình: \(2\sin 2x\cos 2x + \sqrt 3 \cos 4x + \sqrt 2 = 0\)
Đáp án: D Phương pháp giải: Lời giải chi tiết: \(2\sin 2x\cos 2x + \sqrt 3 \cos 4x + \sqrt 2 = 0 \Leftrightarrow \sin 4x + \sqrt 3 .\cos 4x = - \sqrt 2 \) Chia cả 2 vế cho \(\sqrt {1 + {{\left( {\sqrt 3 } \right)}^2}} = 2\) , ta có: \(\begin{array}{l}\frac{1}{2}.\sin 4x + \frac{{\sqrt 3 }}{2}.cos4x = - \frac{{\sqrt 2 }}{2} \Leftrightarrow \sin \left( {4x + \frac{\pi }{3}} \right) = - \frac{{\sqrt 2 }}{2}\\ \Leftrightarrow \left[ \begin{array}{l}4x + \frac{\pi }{3} = - \frac{\pi }{4} + k2\pi \\4x + \frac{\pi }{3} = \pi - \left( { - \frac{\pi }{4}} \right) + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \frac{{7\pi }}{{48}} + \frac{{k\pi }}{2}\\x = \frac{{11\pi }}{{48}} + \frac{{k\pi }}{2}\end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\) KL: \(x \in \left\{ {\frac{{ - 7\pi }}{{48}} + \frac{{k\pi }}{2};\frac{{11\pi }}{{48}} + \frac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\). Chọn D. Câu hỏi 34 : Giải phương trình: \(\cos x - \sqrt 3 \sin x = 2\cos 3x.\)
Đáp án: C Phương pháp giải: Lời giải chi tiết: Chia cả 2 vế cho \(\sqrt {1 + {{\left( {\sqrt 3 } \right)}^2}} = 2\), ta có: \(\begin{array}{l}\frac{1}{2}.\cos x - \frac{{\sqrt 3 }}{2}.\sin x = \cos 3x \Leftrightarrow \cos \left( {x + \frac{\pi }{3}} \right) = \cos 3x\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{3} = 3x + k2\pi \\x + \frac{\pi }{3} = - 3x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} - k\pi \\x =- \frac{\pi }{{12}} + \frac{{k\pi }}{2}\end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\) KL: \(x \in \left\{ {\frac{\pi }{6} - k\pi ;-\frac{\pi }{{12}} + \frac{{k\pi }}{2};k \in \mathbb{Z}} \right\}\) . Chọn C. Câu hỏi 35 : Số các giá trị nguyên của tham số \(m\) để phương trình \(m\sin x + 3\cos x = 2m\) có nghiệm là:
Đáp án: D Phương pháp giải: Phương trình dạng \(a\sin x + b\cos x = c\) có nghiệm \( \Leftrightarrow {a^2} + {b^2} \ge {c^2}\). Lời giải chi tiết: Phương trình \(m\sin x + 3\cos x = 2m\)có nghiệm \( \Leftrightarrow {m^2} + {3^2} \ge {\left( {2m} \right)^2}\). \( \Leftrightarrow 3{m^2} \le 9 \Leftrightarrow {m^2} \le 3 \Leftrightarrow - \sqrt 3 \le m \le \sqrt 3 \). Lại có \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 1;0;1} \right\}\). Chọn D. Câu hỏi 36 : Giải phương trình \(2\tan x + \cot x - 3 = 0.\)
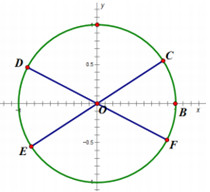
Đáp án: C Phương pháp giải: Lời giải chi tiết: \(2\tan x + \cot x - 3 = 0\) (ĐK: \(x \ne k\pi ;\,\,x \ne \dfrac{\pi }{2} + k\pi \)). Đặt \(\tan x = t \to 2t + \dfrac{1}{t} - 3 = 0\) \(\begin{array}{l} \Leftrightarrow 2{t^2} - 3t + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = \dfrac{1}{2}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\tan x = 1\\\tan x = \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{4} + k\pi \\x = \arctan \left( {\dfrac{1}{2}} \right) + k\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\) Câu hỏi 37 : Xét đường tròn lượng giác như hình vẽ,biết \(\widehat {BOC} = \widehat {BOF} = {30^0}\) lần lượt là các điểm đối xứng với \(C,\,\,F\) qua gốc \(O\). Nghiệm của phương trình \(2\sin x - 1 = 0\) được biểu diễn trên đường tròn lượng giác là những điểm nào?
Đáp án: A Phương pháp giải: Giải phương trình lượng giác cơ bản \(\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\). Lời giải chi tiết: \(2\sin x - 1 = 0 \Leftrightarrow \sin x = \dfrac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\). Các điểm biểu diễn hai họ nghiệm trên là điểm \(C\) và điểm \(D\). Chọn A. Câu hỏi 38 : Giải phương trình \(4{\sin ^4}x + 12{\cos ^2}x - 7 = 0\) có nghiệm là:
Đáp án: B Phương pháp giải: Giải phương trình trùng phương đối với một hàm số lượng giác, sử dụng công thức \({\cos ^2}x = 1 - {\sin ^2}x\). Lời giải chi tiết: \(\begin{array}{l}4{\sin ^4}x + 12{\cos ^2}x - 7 = 0 \Leftrightarrow 4{\sin ^4}x + 12\left( {1 - {{\sin }^2}x} \right) - 7 = 0\\ \Leftrightarrow 4{\sin ^4}x - 12{\sin ^2}x + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}{\sin ^2}x = \dfrac{5}{2}\,\,\left( {loai} \right)\\{\sin ^2}x = \dfrac{1}{2}\,\,\left( {tm} \right)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\sin x = \dfrac{{\sqrt 2 }}{2}\\\sin x = - \dfrac{{\sqrt 2 }}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{4} + k2\pi \\x = \dfrac{{3\pi }}{4} + k2\pi \\x = - \dfrac{\pi }{4} + k2\pi \\x = \dfrac{{5\pi }}{4} + k2\pi \end{array} \right. \Leftrightarrow x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\) Chọn B. Câu hỏi 39 : Phương trình \(1 + \sin x - \cos x - \sin 2x = 0\) có bao nhiêu nghiệm trên \(\left[ {0;\dfrac{\pi }{2}} \right)\)?
Đáp án: A Phương pháp giải: - Đặt \(t = \sin x - \cos x\,\,\left( { - \sqrt 2 \le t \le \sqrt 2 } \right) \Rightarrow \sin x\cos x = \dfrac{{1 - {t^2}}}{2}\). - Giải phương trình bậc hai đối với \(t\), sau đó tìm nghiệm \(x\). - Tìm các nghiệm thuộc khoảng đề bài cho. Lời giải chi tiết: \(1 + \sin x - \cos x - \sin 2x = 0 \Leftrightarrow 1 + \sin x - \cos x - 2\sin x\cos x = 0\). Đặt \(t = \sin x - \cos x\,\,\left( { - \sqrt 2 \le t \le \sqrt 2 } \right) \Rightarrow \sin x\cos x = \dfrac{{1 - {t^2}}}{2}\). Khi đó phương trình trở thành: \(1 + t + 1 - {t^2} = 0 \Leftrightarrow {t^2} - t - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 2\,\,\,\,\left( {ktm} \right)\\t = - 1\,\,\left( {tm} \right)\end{array} \right.\). Với \(t = - 1\) ta có: \(\begin{array}{l}\sin x - \cos x = - 1 \Leftrightarrow \sin \left( {x - \dfrac{\pi }{4}} \right) = - \dfrac{1}{{\sqrt 2 }}\\ \Leftrightarrow \left[ \begin{array}{l}x - \dfrac{\pi }{4} = - \dfrac{\pi }{4} + k2\pi \\x - \dfrac{\pi }{4} = \dfrac{{5\pi }}{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k2\pi \\x = \dfrac{{3\pi }}{2} + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\) Xét họ nghiệm \(x = k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\) thuộc \(\left[ {0;\dfrac{\pi }{2}} \right)\) ta có: \(0 \le k2\pi < \dfrac{\pi }{2} \Leftrightarrow 0 \le k < \dfrac{1}{4}\,\,\left( {k \in \mathbb{Z}} \right) \Rightarrow k = 0 \Rightarrow x = 0\). Xét họ nghiệm \(x = \dfrac{{3\pi }}{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\) thuộc \(\left[ {0;\dfrac{\pi }{2}} \right)\) ta có: \(0 \le \dfrac{{3\pi }}{2} + k2\pi < \dfrac{\pi }{2} \Leftrightarrow 0 \le \dfrac{3}{2} + 2k < \dfrac{1}{2} \Leftrightarrow - \dfrac{3}{4} \le k < - \dfrac{1}{2}\,\,\left( {k \in \mathbb{Z}} \right) \Rightarrow k \in \emptyset \). Vậy phương trình có duy nhất 1 nghiệm \(x\) thỏa mãn yêu cầu bài toán. Chọn A Câu hỏi 40 : Giải phương trình \({\left( {\sin x + \cos x} \right)^2} - \sqrt 2 \left( {\sin 2x + 1} \right) + \sin x + \cos x = - \sqrt 2 \).
Đáp án: D Phương pháp giải: Đặt \(t = \sin x + \cos x\,\,\left( { - \sqrt 2 \le t \le \sqrt 2 } \right) \Rightarrow \sin x\cos x = \dfrac{{{t^2} - 1}}{2}\). Lời giải chi tiết: \(\begin{array}{l}\,\,\,\,\,\,{\left( {\sin x + \cos x} \right)^2} - \sqrt 2 \left( {\sin 2x + 1} \right) + \sin x + \cos x = - \sqrt 2 \\ \Leftrightarrow {\left( {\sin x + \cos x} \right)^2} - \sqrt 2 \left( {2\sin x\cos x + 1} \right) + \sin x + \cos x = - \sqrt 2 \end{array}\) Đặt \(t = \sin x + \cos x\,\,\left( { - \sqrt 2 \le t \le \sqrt 2 } \right) \Rightarrow \sin x\cos x = \dfrac{{{t^2} - 1}}{2}\). Khi đó phương trình trở thành: \({t^2} - \sqrt 2 \left( {{t^2} - 1 + 1} \right) + t = \sqrt 2 \Leftrightarrow \left( {1 - \sqrt 2 } \right){t^2} + t + \sqrt 2 = 0 \Leftrightarrow \left[ \begin{array}{l}t = - 1\,\,\,\,\,\,\,\,\,\,\,\,\left( {tm} \right)\\t = 2 + \sqrt 2 \,\,\left( {ktm} \right)\end{array} \right.\) Khi \(t = - 1 \Rightarrow \sin x + \cos x = - 1 \Leftrightarrow \sin \left( {x + \dfrac{\pi }{4}} \right) = - \dfrac{1}{{\sqrt 2 }}\) \( \Leftrightarrow \left[ \begin{array}{l}x + \dfrac{\pi }{4} = - \dfrac{\pi }{4} + k2\pi \\x + \dfrac{\pi }{4} = \dfrac{{5\pi }}{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{\pi }{2} + k2\pi \\x = \pi + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\). Chọn D Quảng cáo
|