40 bài tập trắc nghiệm mặt cầu mức độ thông hiểuLàm bàiQuảng cáo
Câu hỏi 1 : Cho khối cầu có thể tích \(V = 4\pi {a^3}\,\,\,\left( {a > 0} \right),\) bán kính \(R\) của khối cầu trên theo \(a\) là:
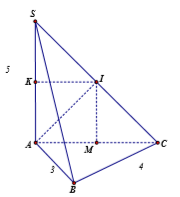
Đáp án: B Phương pháp giải: Thể tích của khối cầu có bán kính \(R\) là: \(V = \dfrac{4}{3}\pi {R^3}.\) Lời giải chi tiết: Thể tích khối cầu đã cho là: \(V = 4\pi {a^3}\) \( \Leftrightarrow \dfrac{4}{3}\pi {R^3} = 4\pi {a^3}\) \( \Leftrightarrow {R^3} = 3{a^3} \Leftrightarrow R = a\sqrt[3]{3}\) Chọn B. Câu hỏi 2 : Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(B\), \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\), \(SA = 5\), \(AB = 3\), \(BC = 4\). Bán kính \(R\) của mặt cầu ngoại tiếp hình chóp \(S.ABC\) bằng:
Đáp án: A Phương pháp giải: - Xác định điểm cách đều tất cả các đỉnh \(S,\,\,A,\,\,B,\,\,C\). - Sử dụng định lí Pytago để tính bán kính. Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(AC\). Vì tam giác \(ABC\) vuông tại \(B\) nên \(M\) là tâm đường tròn ngoại tiếp \(\Delta ABC\) Qua \(M\) dựng đường thẳng \(d\parallel SA,\,\,d \cap SC = \left\{ I \right\}\), khi đó ta có \(IA = IB = IC\,\,\,\left( 1 \right)\). Xét tam giác \(SAC\) có: \(M\) là trung điểm \(AC\), \(MI\parallel SA\) \( \Rightarrow I\) là trung điểm của \(SC\) (định lí đường trung bình của tam giác). Mà \(\Delta SAC\) vuông tại \(C\) nên \(I\) là tâm đường tròn ngoại tiếp \(\Delta SAC\) \( \Rightarrow IA = IC = IS\,\,\left( 2 \right)\). Từ (1) và (2) \( \Rightarrow IA = IB = IC = IS\) \( \Rightarrow I\) là tâm mặt cầu ngoại tiếp chóp \(S.ABC\), khối cầu này có bán kính \(R = IA\). Ta có \(IM = \dfrac{1}{2}SA = \dfrac{5}{2}\), \(AM = \dfrac{1}{2}AC = \dfrac{1}{2}\sqrt {{3^2} + {4^2}} = \dfrac{5}{2}\). Áp dụng định lí Pytago trong tam giác vuông \(AIM\) có: \(R = IA = \sqrt {A{M^2} + I{M^2}} = \sqrt {\dfrac{{25}}{4} + \dfrac{{25}}{4}} = \dfrac{{5\sqrt 2 }}{2}\). Chọn A. Câu hỏi 3 : Cho mặt cầu \(\left( {{S_1}} \right)\)có bán kính \({R_1}\), mặt cầu \(\left( {{S_2}} \right)\)có bán kính \({R_2} = 2{R_1}.\) Tính tỉ số diện tích của mặt cầu \(\left( {{S_2}} \right)\) và \(\left( {{S_1}} \right).\)
Đáp án: A Phương pháp giải: Công thức diện tích mặt cầu bán kính R là: \(S = 4\pi {R^2}\). Lời giải chi tiết: Ta có: \(\dfrac{{{S_2}}}{{{S_1}}} = \dfrac{{4\pi R_2^2}}{{4\pi R_1^2}} = \dfrac{{R_2^2}}{{R_1^2}} = {2^2} = 4\). Chọn A. Câu hỏi 4 : Cho khối cầu có bán kính \(R = 2.\) Thể tích của khối cầu đã cho bằng:
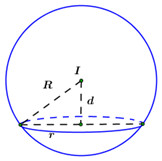
Đáp án: B Phương pháp giải: Thể tích của khối cầu có bán kính \(R\) là:\(V = \dfrac{4}{3}\pi {R^3}.\) Lời giải chi tiết: Thể tích của khối cầu đã cho là: \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {.2^3} = \dfrac{{32\pi }}{3}.\) Chọn B. Câu hỏi 5 : Khối cầu có thể tích \(\dfrac{{32\pi {a^3}}}{3}\) thì bán kính bằng:
Đáp án: C Phương pháp giải: Khối cầu có bán kính \(R\) thì có thể tích \(V = \dfrac{4}{3}\pi {R^3}\) Lời giải chi tiết: Gọi bán kính là \(R\) Ta có: \(V = \dfrac{{32\pi {a^3}}}{3}\) nên \(\dfrac{4}{3}\pi {R^3} = \dfrac{{32}}{3}\pi {a^3}\)\( \Leftrightarrow {R^3} = 8{a^3} \Leftrightarrow R = 2a\) Chọn C. Câu hỏi 6 : Cho mặt cầu \(S\left( {I;R} \right)\) và mặt phẳng \(\left( P \right)\) cách I một khoảng bằng \(\frac{R}{2}\). Khi đó giao của \(\left( P \right)\) và \(\left( S \right)\) là đường tròn có chu vi bằng:
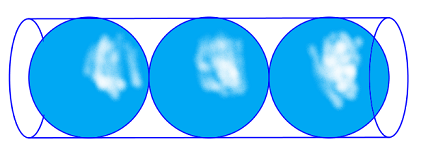
Đáp án: C Phương pháp giải: Giao tuyến của mặt cầu tâm I và mặt phẳng \(\left( P \right)\) là đường tròn có bán kính bằng: \(r = \sqrt {{R^2} - d_{\left( {I;\left( p \right)} \right)}^2} \) Áp dụng công thức tính chu vi đường tròn. Lời giải chi tiết: Ta thấy \(d\left( {I;\left( P \right)} \right) = \frac{R}{2} \Rightarrow r = \sqrt {{R^2} - d_{\left( {I;\left( p \right)} \right)}^2} = \frac{{R\sqrt 3 }}{2}\). Khi đó chu vi đường tròn bằng \(S = 2\pi r = R\sqrt 3 \pi \) Chọn C. Câu hỏi 7 : Cho mặt cầu \(\left( S \right)\)có đường kính 10 cm và mặt phẳng \(\left( P \right)\)cách tâm mặt cầu một khoảng 4 cm. Khẳng định nào sau đây sai?
Đáp án: C Phương pháp giải: - Tìm bán kính của mặt cầu. - So sánh bán kính \(R\) của mặt cầu với khoảng cách \(d\) từ tâm đến mặt phẳng \(\left( P \right)\). + Nếu \(R > d\) thì \(\left( P \right)\) cắt \(\left( S \right)\) theo một đường tròn có bán kính \(r = \sqrt {{R^2} - {d^2}} \). + Nếu \(R = d\) thì \(\left( P \right)\) tiếp xúc với \(\left( S \right)\). + Nếu \(R < d\) thì \(\left( P \right)\) và \(\left( S \right)\) không có điểm chung nào. Lời giải chi tiết: Mặt cầu \(\left( S \right)\) có đường kính là 10cm bán kính \(R = 5cm\). Mà khoảng cách từ tâm của mặt cầu và mặt phẳng \(\left( P \right)\) là \(d = 4cm < R\). Do đó mặt phẳng \(\left( P \right)\) cắt \(\left( S \right)\) theo một đường tròn có bán kính \(r = \sqrt {{R^2} - {d^2}} = 3\,\,\left( {cm} \right)\). Vậy trong 4 đáp án chỉ có đáp án C sai. Chọn C. Câu hỏi 8 : Người ta bỏ ba quả bóng bàn cùng kích thước vào trong một chiếc hộp hình trụ có đáy bằng hình tròn lớn của quả bóng bán và chiều cao bằng ba lần đường kính quả bóng bàn. Gọi \({S_1}\) là tổng diện tích ba quả bóng bàn, \({S_2}\) là diện tích xung quanh của hình trụ. Tỉ số \(\dfrac{{{S_1}}}{{{S_2}}}\) bằng
Đáp án: C Phương pháp giải: Diện tích mặt cầu bán kính R là: \(S = 4\pi {R^2}\) Diện tích xung quanh của hình trụ có chiều cao h, bán kính đáy R là: \({S_{xq}} = 2\pi Rh\) Lời giải chi tiết: Giả sử mỗi quả bóng bàn có bán kính là R. Khi đó, bán kính đáy của hình trụ cũng là \(R\), chiều cao của hình trụ là \(6R\). Tổng diện tích ba quả bóng bàn: \({S_1} = 3.\left( {4\pi {R^2}} \right) = 12\pi {R^2}\) Diện tích xung quanh của hình trụ: \({S_2} = 2\pi Rh = 2\pi R.6R = 12\pi {R^2}\)\( \Rightarrow \dfrac{{{S_1}}}{{{S_2}}} = 1\). Chọn C. Câu hỏi 9 : Cho hai khối cầu có bán kính lần lượt bằng a và 2a. Tỉ số thể tích của khối cầu nhỏ với thể tích của khối cầu lớn bằng:
Đáp án: C Phương pháp giải: Công thức tính thể của khối cầu có bán kính \(r:\;\;V = \frac{4}{3}\pi {r^3}.\) Lời giải chi tiết: Thể tích khối cầu có bán kính \(r = a\) là: \({V_1} = \frac{4}{3}\pi {r^3} = \frac{4}{3}\pi {a^3}.\) Thể tích khối cầu có bán kính \(R = 2a\) là: \({V_2} = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {2a} \right)^3} = \frac{{32}}{3}\pi {a^3}.\) \( \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{4}{3}\pi {a^3}}}{{\frac{{32}}{3}\pi {a^3}}} = \frac{4}{{32}} = \frac{1}{8}.\) Chọn C. Câu hỏi 10 : Nếu tăng bán kính của mặt cầu lên 4 lần thì diện tích mặt cầu tăng lên bao nhiêu lần?
Đáp án: A Phương pháp giải: Công thức tính diện tích mặt cầu bán kính \(R\) là: \(S = 4\pi {R^2}.\) \( \Rightarrow \) Nếu tăng bán kính mặt cầu lên \(k\) lần thì diện tích mặt cầu tăng \({k^2}\) lần. Lời giải chi tiết: Tăng bán kính mặt cầu lên 4 lần thì diện tích mặt cầu tăng 16 lần. Chọn A. Câu hỏi 11 : Khối cầu có bán kính bằng 3 thì có thể tích bằng:
Đáp án: A Phương pháp giải: Công thức tính thể của khối cầu có bán kính \(r:\;\;V = \dfrac{4}{3}\pi {r^3}.\) Lời giải chi tiết: Khối cầu có bán kính bằng 3 thì có thể tích bằng: \(V = \dfrac{4}{3}\pi {r^3} = \dfrac{4}{3}\pi {.3^3} = 36\pi .\) Chọn A. Câu hỏi 12 : Cho khối cầu có thể tích bằng \(36\pi .\) Diện tích mặt cầu đã cho bằng:
Đáp án: B Phương pháp giải: Tính bán kính mặt cầu thông qua công thức tính thể tích khối cầu bán kính \(R\) là: \(V = \frac{4}{3}\pi {R^2}.\) Diện tích mặt cầu có bán kính \(R\) là: \(S = 4\pi {R^2}.\) Lời giải chi tiết: Theo đề bài ta có: \(V = 36\pi \) \( \Leftrightarrow \frac{4}{3}\pi {R^3} = 36\pi \)\( \Leftrightarrow {R^3} = 27\)\( \Leftrightarrow R = 3\) Diện tích mặt cầu đã cho là: \(S = 4\pi {R^2} = 4\pi {.3^2} = 36\pi .\) Chọn B. Câu hỏi 13 : HÌnh chóp \(S.ABC\) có \(SA,\)\(SB,\)\(SC\) đôi một vuông góc và \(SA = 4;SB = 5;SC = 7\). Bán kính mặt cầu ngoại tiếp hình chóp \(S.ABC\) bằng :
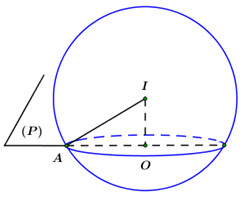
Đáp án: A Phương pháp giải: Hình chóp \(S.ABC\) có 2 cạnh \(SA,SB,SC\) đôi một vuông góc nên bán kính mặt cầu ngoại tiếp hình chóp được tính bởi công thức : \(R = \dfrac{1}{2}\sqrt {S{A^2} + S{B^2} + S{C^2}} \). Lời giải chi tiết: Hình chóp \(S.ABC\) có 2 cạnh \(SA,SB,SC\) đôi một vuông góc nên bán kính mặt cầu ngoại tiếp hình chóp là : \(R = \dfrac{1}{2}\sqrt {S{A^2} + S{B^2} + S{C^2}} = \dfrac{1}{2}\sqrt {{4^2} + {5^2} + {7^2}} = \dfrac{{3\sqrt {10} }}{2}\). Chọn A. Câu hỏi 14 : Thể tích \(V\) của khối cầu có đường kính \(4\,cm\) là
Đáp án: D Phương pháp giải: Thể tích khối cầu bán kính \(R\) là \(V = \dfrac{4}{3}\pi {R^3}\) Lời giải chi tiết: Thể tích \(V = \dfrac{4}{3}\pi {.2^3} = \dfrac{{32\pi }}{3}\left( {c{m^3}} \right)\) Chọn B. Câu hỏi 15 : Cho mặt cầu \(\left( S \right)\) có tâm \(I,\) bán kính \(R = \sqrt 3 \) và điểm \(A\) thuộc \(\left( S \right).\) Gọi \(\left( P \right)\) là mặt phẳng đi qua \(A\) và tạo với \(IA\) một góc bằng \(\alpha .\) Biết rằng \(\sin \alpha = \dfrac{1}{3}.\) Tính diện tích của hình tròn có biên là đường tròn giao tuyến của mặt phẳng \(\left( P \right)\) và mặt cầu \(\left( S \right).\)
Đáp án: B Phương pháp giải: Công thức tính diện tích đường tròn bán kính \(R\) là: \(S = \pi {R^2}.\) Lời giải chi tiết:
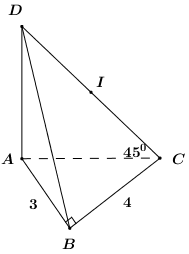
Gọi \(O\) là tâm đường tròn giao tuyến của \(\left( P \right)\) và \(\left( S \right)\) \( \Rightarrow IO \bot \left( P \right).\) Khi đó ta có: \(\angle \left( {IA;\,\,\left( P \right)} \right) = \angle \left( {IA,\,\,OA} \right) = \angle IAO.\) \(\begin{array}{l} \Rightarrow \sin \angle IAO = \dfrac{1}{3} \Leftrightarrow \dfrac{{OI}}{{IA}} = \dfrac{1}{3} \Rightarrow OI = \dfrac{{\sqrt 3 }}{3}.\\ \Rightarrow AO = r = \sqrt {I{A^2} - O{I^2}} = \sqrt {{{\left( {\sqrt 3 } \right)}^2} - {{\left( {\dfrac{{\sqrt 3 }}{3}} \right)}^2}} = \dfrac{{2\sqrt 6 }}{3}\\ \Rightarrow {S_{\left( O \right)}} = \pi {r^2} = \pi {\left( {\dfrac{{2\sqrt 6 }}{3}} \right)^2} = \dfrac{{8\pi }}{3}.\end{array}\) Chọn B. Câu hỏi 16 : Cho tứ diện \(ABCD\) có cạnh \(AD\) vuông góc với mặt phẳng \(\left( {ABC} \right)\), tam giác \(ABC\) vuông tại \(B\) có cạnh \(AB = 3;\)\(BC = 4\) và góc giữa \(DC\) và mặt phẳng \(\left( {ABC} \right)\) bằng \({45^0}\). Tính thể tích mặt cầu ngoại tiếp tứ diện.
Đáp án: C Phương pháp giải: - Gọi \(I\) là trung điểm của \(CD\), sử dụng định lí: Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền chứng minh \(I\) là tâm mặt cầu ngoại tiếp tứ diện ... - Áp dụng định lí Pytago và các tỉ số lượng giác của góc nhọn trong tam giác vuông để tính bán kính khối cầu. - Sử dụng công thức: Thể tích khối cầu bán kính \(R\) là: \(V = \dfrac{4}{3}\pi {R^3}\). Lời giải chi tiết:
Gọi \(I\) là trung điểm của \(CD\). Ta có \(\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot AD\,\,\left( {AD \bot \left( {ABC} \right)} \right)\end{array} \right.\)\( \Rightarrow BC \bot \left( {ABD} \right) \Rightarrow BC \bot BD.\) Suy ra \(\Delta BCD\) vuông tại \(B\) \( \Rightarrow IB = IC = ID\) (tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền). Lại có \(\Delta ACD\) vuông tại \(A\) (do \(AD \bot \left( {ABC} \right) \Rightarrow AD \bot AC\)) \( \Rightarrow IA = IC = ID\). Do đó \(IA = IB = IC = ID\) hay \(I\) là tâm mặt cầu ngoại tiếp tứ diện \(ABCD\). Khi đó bán kính mặt cầu là \(R = IC = \dfrac{{CD}}{2}.\) Ta có: \(AD \bot \left( {ABC} \right)\) nên \(AC\) là hình chiếu của \(CD\) lên \(\left( {ABC} \right)\) \( \Rightarrow \angle \left( {CD;\left( {ABC} \right)} \right) = \angle \left( {CD;CA} \right) = \angle ACD = {45^0}\). Xét tam giác vuông \(ABC\) có: \(AC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{3^2} + {4^2}} = 5\) (định lí Pytago). Xét tam giác vuông \(ACD\) có: \(CD = \dfrac{{AC}}{{\cos {{45}^0}}} = 5\sqrt 2 \) \( \Rightarrow R = \dfrac{{5\sqrt 2 }}{2}\). Vậy thể tích khối cầu ngoại tiếp tứ diện \(ABCD\) là: \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{{125\sqrt 2 }}{3}\pi .\) Chọn C. Câu hỏi 17 : Mặt cầu \(\left( S \right)\) tâm O có diện tích bằng \(400\pi \,c{m^2}\). Mặt phẳng \(\left( P \right)\) cách tâm O một khoảng bằng 6cm và cắt mặt cầu \(\left( S \right)\) theo thiết diện là một đường tròn. Tính bán kính \(r\) của đường tròn đó.
Đáp án: A Phương pháp giải: Sử dụng công thức: \({d^2} + {r^2} = {R^2}\)
Trong đó, \(d\,\) : khoảng cách từ tâm O đến mặt phẳng (P), \(r\): bán kính đường tròn là giao tuyến của mặt cầu (S) và mặt phẳng (P), \(R\): bán kính hình cầu. Lời giải chi tiết: Gọi \(R,\,\,r\) lần lượt là bán kính mặt cầu và bán kính đường tròn giao tuyến giữa \(\left( P \right)\) và \(\left( S \right)\). Ta có: \({S_{cau}} = 4\pi {R^2} = 400\pi \,\,\,\left( {c{m^2}} \right) \Rightarrow r = 10\,\,\,\left( {cm} \right).\) Gọi \(d = d\left( {O;\left( P \right)} \right) \Rightarrow d = 6\,\,\left( {cm} \right)\). Ta có: \({d^2} + {r^2} = {R^2} \Rightarrow {6^2} + {r^2} = {10^2} \Rightarrow r = 8\,\,\,\left( {cm} \right).\) Chọn A. Câu hỏi 18 : Trong không gian cho hai điểm phân biệt A, B cố định. Tập hợp các điểm M thỏa mãn đẳng thức \(\overrightarrow {MA} .\overrightarrow {MB} = 0\) là:
Đáp án: C Phương pháp giải: Biến đổi đẳng thức vecto bài cho, từ đó suy ra tập hợp các điểm \(M.\) Lời giải chi tiết: Ta có: \(\overrightarrow {MA} .\overrightarrow {MB} = 0\) Gọi \(I\) là trung điểm của \(AB.\) \(\begin{array}{l} \Rightarrow \overrightarrow {MA} .\overrightarrow {MB} = 0 \Leftrightarrow \left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right) = 0\\ \Leftrightarrow {\overrightarrow {MI} ^2} + \overrightarrow {MI} .\overrightarrow {IB} + \overrightarrow {IA} .\overrightarrow {MI} + \overrightarrow {IA} .\overrightarrow {IB} = 0\\ \Leftrightarrow M{I^2} + \overrightarrow {MI} \left( {\overrightarrow {IB} + \overrightarrow {IA} } \right) + IA.IB.\cos \left( {\overrightarrow {IA} ,\,\overrightarrow {IB} } \right) = 0\\ \Leftrightarrow M{I^2} + I{A^2}\cos {180^0} = 0\\ \Leftrightarrow M{I^2} = I{A^2}\\ \Leftrightarrow MI = IA\end{array}\) Vậy tập hợp điểm \(M\) thỏa mãn bài toán là mặt cầu tâm \(I,\) đường kính \(AB.\) Chọn C. Câu hỏi 19 : Trong các hình chóp tứ giác sau, hình chóp nào có mặt cầu ngoại tiếp:
Đáp án: B Phương pháp giải: Hình chóp muốn có mặt cầu ngoại tiếp thì tất cả các mặt của hình chóp đều phải có đường tròn ngoại tiếp. Lời giải chi tiết: Trong các hình: Hình thang vuông, hình thang cân, hình bình hành, hình thang, chỉ có duy nhất hình thang cân là tứ giác có đường tròn nội tiếp. Vậy trong 4 đáp án chỉ có hình chóp có đáy là hình thang cân có mặt cầu ngoại tiếp. Chọn B. Câu hỏi 20 : Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên \(A'A = a\sqrt 2 .\) Mặt cầu đi qua tất cả các đỉnh của khối họp chữ nhật có bán kính bằng :
Đáp án: A Phương pháp giải: - Tìm tâm của mặt cầu ngoại tiếp hình lập phương. - Áp dụng định lí Pytago để tính bán kính của mặt cầu. Lời giải chi tiết: Gọi \(O,\,\,O'\) lần lượt là tâm của hình vuông \(ABCD,\,\,A'B'C'D'\). Gọi \(I\) là trung điểm của \(OO'\). Suy ra \(I\) cách đều 8 đỉnh của hình lập phương nên \(I\) là tâm mặt cầu cần tìm. Hình vuông \(ABCD\) có cạnh bằng \(a\)\( \Rightarrow AO = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}.\) Mặt khác: \(OI = \frac{{A'A}}{2} = \frac{{a\sqrt 2 }}{2}.\) Áp dụng định lí Pytago trong tam giác vuông \(AOI\) có: \(AI = \sqrt {A{O^2} + O{I^2}} = \sqrt {{{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = a\) Chọn A. Câu hỏi 21 : Một hình lập phương cạnh \(a\) có bán kính mặt cầu ngoại tiếp bằng
Đáp án: D Phương pháp giải: Bán kính mặt cầu ngoại tiếp hình lập phương bằng nửa đường chéo của hình lập phương đó. Lời giải chi tiết: Hình lập phương cạnh \(a\) có đường chéo bằng \(a\sqrt 3 \). Vậy bán kính mặt cầu ngoại tiếp hình lập phương là \(R = \dfrac{{a\sqrt 3 }}{2}\). Đáp án D. Câu hỏi 22 : Cho mặt cầu có diện tích là S, thể tích khối cầu đó là V. Bán kính R của mặt cầu là
Đáp án: D Phương pháp giải: Sử dụng công thức tính diện tích và thể tích hình cầu. Lời giải chi tiết: Diện tích hình cầu là \(S = 4\pi {R^2}\) Thể tích hình cầu là \(V=\frac{4}{3}\pi R^{3}\) Chia từng vế của hai phương trình trên ta có: \(R = \frac{{3V}}{S}.\) Chọn D. Câu hỏi 23 : Trong không gian, cho hai điểm phân biệt A và B. Tập hợp tâm các mặt cầu đi qua A và B là
Đáp án: A Phương pháp giải: Dạng bài về tìm quỹ tích Lời giải chi tiết: Gọi \(I\) là tâm mặt cầu đi qua \(A,\,\,B \Rightarrow IA = IB\). \( \Rightarrow I\) nằm trên mặt phẳng trung trực của \(AB\). Chọn A. Câu hỏi 24 : Mặt cầu \(\left( S \right)\) tâm \(O\) có diện tích bằng \(400\pi \)\(c{m^2}\), mặt phẳng \(\left( P \right)\) cách tâm \(O\) một khoảng bằng \(6cm\) và cắt mặt cầu \(\left( S \right)\) theo một thiết diện là đường tròn. Tính bán kính \(r\) của đường tròn đó
Đáp án: D Phương pháp giải: - Diện tích của mặt cầu có bán kính bằng \(R\) là \(S = 4\pi {R^2}\). - Áp dụng định lí Pytago tính bán kính \(r\) của đường tròn. Lời giải chi tiết:
Gọi \(I\) là tâm thiết diện khi cắt mặt cầu \(\left( S \right)\) bởi mặt phẳng \(\left( P \right)\), \(AB\) là đường kính của đường tròn. Gọi \(R\) là bán kính của mặt cầu \(\left( S \right)\). Diện tích của mặt cầu bằng \(400\pi \left( {c{m^2}} \right)\) nên : \(S = 400\pi \Leftrightarrow 4\pi {R^2} = 400\pi \Rightarrow R = 10\left( {cm} \right)\) \(A,B\) nằm trên đường tròn nên \(A,B\) cũng nằm trên mặt cầu hay \(OA = OB = R = 10\,\,\,\left( {cm} \right)\) Khoảng cách từ tâm \(O\) đến mặt phẳng \(\left( P \right)\) là \(OI = 6\left( {cm} \right)\). Áp dụng định lí Pytago trong tam giác \(OIA\) vuông tại \(I\) ta có: \(O{I^2} + I{A^2} = O{A^2} \Leftrightarrow {6^2} + I{A^2} = {10^2} \Leftrightarrow IA = 8\,\,\,\left( {cm} \right)\). Vậy bán kính \(r\) của đường tròn là \(r = IA = 8\left( {cm} \right)\). Chọn D. Câu hỏi 25 : Nếu tăng bán kính của một khối cầu gấp 2 lần thì thể tích thay đổi như thế nào?
Đáp án: C Phương pháp giải: Thể tích khối cầu bán kính \(R\) là \(V = \frac{4}{3}\pi {R^3}\). Lời giải chi tiết: Gọi bán kính khối cầu là \(R\). Diện tích ban đầu của khối cầu là \(V = \frac{4}{3}\pi {R^3}\). Sau khi tăng bán kính gấp 2 lần thì bán kính mới của khối cầu là \(R' = 2R\). Diện tích mới của khối cầu là \(V' = \frac{4}{3}\pi R{'^3}\). Ta có: \(\frac{{V'}}{V} = \frac{{\frac{4}{3}\pi R{'^3}}}{{\frac{4}{3}\pi {R^3}}} = {\left( {\frac{{R'}}{R}} \right)^3} = {\left( {\frac{{2R}}{R}} \right)^3} = 8 \Rightarrow \Rightarrow V' = 8V\). Vậy khi tăng bán kính của một khối cầu gấp 2 lần thì thể tích khối cầu tăng gấp 8 lần. Chọn C. Câu hỏi 26 : Cho hình chóp đều \(S.ABCD\) có \(ABCD\) là hình vuông cạnh \(2a\) và \(SA \bot SC.\) Bán kính mặt cầu ngoại tiếp hình chóp đều đã cho bằng:
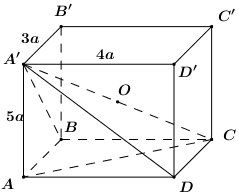
Đáp án: B Phương pháp giải: Tâm mặt cầu ngoại tiếp hình chóp là điểm cách đều tất cả các đỉnh của hình chóp. Lời giải chi tiết: Gọi \(O = AC \cap BD \Rightarrow OA = OB = OC = OC\). Xét tam giác vuông \(SAC\) có trung tuyến \(SO \Rightarrow OS = \frac{1}{2}AC = OA = OC\). \( \Rightarrow OA = OB = OC = OD = OS\). \( \Rightarrow O\) là tâm mặt cầu ngoại tiếp khối chóp \(S.ABC\) và bán kính khối cầu là \(R = OA\). Vì \(ABCD\) là hình vuông cạnh \(2a\) nên \(AC = 2a\sqrt 2 \Rightarrow OA = a\sqrt 2 \). Vậy \(R = a\sqrt 2 \). Chọn B. Câu hỏi 27 : Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = 3a,\,\,AD = 4a,\,\,AA' = 5a\). Bán kính mặt cầu ngoại tiếp hình chóp \(A'.ABCD\) bằng:
Đáp án: C Phương pháp giải: Thể tích khối nón chiều cao \(h\), bán kính đáy \(r\) là \(V = \frac{1}{3}\pi {r^2}h\). Lời giải chi tiết: Gọi \(O\) là trung điểm của \(A'C\), khi đó \(O\) là tâm mặt cầu ngoại tiếp khối hộp chữ nhật \(ABCD.A'B'C'D'\). \( \Rightarrow OA' = OA = OB = OC = OD \Rightarrow O\) cũng là tâm mặt cầu ngoại tiếp chóp \(A'ABCD\). Áp dụng định lí Pytago trong tam giác vuông \(ABC\) ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{\left( {3a} \right)}^2} + {{\left( {4a} \right)}^2}} = 5a\). Áp dụng định lí Pytago trong tam giác vuông \(A'AC\) có: \(A'C = \sqrt {AA{'^2} + A{C^2}} = \sqrt {{{\left( {5a} \right)}^2} + {{\left( {5a} \right)}^2}} = 5a\sqrt 2 \). Vậy bán kính mặt cầu ngoại tiếp chóp \(A'.ABCD\) là \(R = \frac{1}{2}A'C = \frac{{5a\sqrt 2 }}{2}\). Chọn C. Câu hỏi 28 : Cho hình chóp tam giác đều \(S.ABC\) có cạnh đáy bằng \(a\) và mỗi cạnh bên bằng \(a\sqrt 2 \). Khi đó bán kính mặt cầu ngoại tiếp hình chóp \(S.ABC\) là:
Đáp án: C Phương pháp giải: Lời giải chi tiết:
\( + )\)\(S.ABC\) là chóp tam giác đều \( \Rightarrow \Delta ABC\) đều. \( \Rightarrow AG = \dfrac{2}{3}.AH = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\) \( + )\)Xét \(\Delta SGA\)có: \(S{G^2} + A{G^2} = S{A^2}\) \( \Rightarrow SG = \sqrt {2{a^2} - \dfrac{{{a^2}.3}}{9}} = \dfrac{{a\sqrt 5 }}{{\sqrt 3 }}\) \( \Rightarrow {R_{mcnt}} = \dfrac{{S{A^2}}}{{2.SG}} = \dfrac{{{{\left( {a\sqrt 2 } \right)}^2}}}{{2.\dfrac{{a\sqrt 5 }}{{\sqrt 3 }}}} = \dfrac{{a\sqrt {15} }}{5}\). Chọn C Câu hỏi 29 : Cho hình chóp tam giác đều \(S.ABC\). Biết \(SA = a\) và \(\widehat {ASB} = {90^0}\). Tính theo \(a\) bán kính \(R\) của mặt cầu ngoại tiếp hình chóp \(S.ABC\).
Đáp án: A Phương pháp giải: Lời giải chi tiết:
\( + )\)Xét \(\Delta SAB\)có: \(\left\{ \begin{array}{l}\widehat S = {90^0}\\SA = SB\end{array} \right. \Rightarrow \Delta SAB\)vuông cân tại \(S\). \( \Rightarrow AB = \sqrt {S{A^2} + S{B^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \) \( + )\) Lại có \(\Delta ABC\)đều \( \Rightarrow AG = \dfrac{2}{3}AH = \dfrac{2}{3}.\dfrac{{a\sqrt 2 .\sqrt 3 }}{2} = \dfrac{{a\sqrt 6 }}{3}\). \( + )\)Xét \(\Delta SAG\)vuông tại \(G\): \(S{G^2} + A{G^2} = S{A^2}\) \( \Rightarrow SG = \sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 6 }}{3}} \right)}^2}} = \dfrac{{a\sqrt 3 }}{3}\) \( \Rightarrow {R_{mcnt}} = \dfrac{{S{A^2}}}{{2.SG}} = \dfrac{{{a^2}}}{{2.\dfrac{{a\sqrt 3 }}{3}}} = \dfrac{{a\sqrt 3 }}{2}\) Chọn A Câu hỏi 30 : Cho hình chóp \(S.ABCD\) có \(SA = SB = SC = SD = \sqrt 5 \), \(ABCD\)nội tiếp đường tròn có bán kính \(r = 1\). Mặt cầu ngoại tiếp \(S.ABCD\)có bán kính là:
Đáp án: B Phương pháp giải: Lời giải chi tiết:
\( + )\)\(ABCD\) nội tiếp đường tròn có \(r = 1 \Rightarrow OA = 1.\) \( + )\)Xét \(\Delta SOA\) có: \(S{A^2} = S{O^2} + O{A^2}\) \( \Rightarrow S{O^2} = S{A^2} - O{A^2} = 5 - 1 = 4 \Rightarrow SO = 2\) \( + )\)\({R_{mcnt}} = \dfrac{{S{A^2}}}{{2.SO}} = \dfrac{{{{\left( {\sqrt 5 } \right)}^2}}}{{2.2}} = \dfrac{5}{4}\) Chọn B Câu hỏi 31 : Cho mặt cầu \(S(I;R)\) và mặt phẳng \((P)\) cách \(I\) một khoảng bằng \(\dfrac{R}{2}\). Khi đó thiết diện của \((P)\) và \(\left( S \right)\) là một đường tròn có bán kính bằng:
Đáp án: B Phương pháp giải: Gọi \(R\) là bán kính mặt cầu\(\left( S \right),\)\(d = d\left( {I;\,\,\left( P \right)} \right)\) là khoảng cách từ tâm \(I\) đến mặt phẳng \(\left( P \right)\) và \(r\) là bán kính đường tròn giao tuyến mà \(\left( P \right)\) cắt \(\left( S \right).\) Khi đó ta có: \(r = \sqrt {{R^2} - {d^2}} .\) Lời giải chi tiết:
Áp dụng công thức: \(r = \sqrt {{R^2} - {d^2}} \) ta có: \(r = \sqrt {{R^2} - {{\left( {\dfrac{R}{2}} \right)}^2}} = \sqrt {\dfrac{{3{R^2}}}{4}} = \dfrac{{R\sqrt 3 }}{2}.\) Chọn B. Câu hỏi 32 : Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a;\,\,AD = 2a;\,\,AA' = 2a\). Bán kính \(R\) của mặt cầu ngoại tiếp hình hộp đã cho là:
Đáp án: C Phương pháp giải: Hình hộp chữ nhật có kích thước \(a \times b \times c\) có bán kính mặt cầu ngoại tiếp là \(R = \dfrac{{\sqrt {{a^2} + {b^2} + {c^2}} }}{2}\). Lời giải chi tiết: Bán kính mặt cầu ngoại tiếp khối hộp là \(R = \dfrac{{\sqrt {A{B^2} + A{D^2} + AA{'^2}} }}{2} = \dfrac{{\sqrt {{a^2} + 4{a^2} + 4{a^2}} }}{2} = \dfrac{{3a}}{2}\). Chọn C. Câu hỏi 33 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang cân, đáy lớn \(AD = 2a\), \(AB = BC = CD = a.\) Cạnh bên \(SA = 2a\) và vuông góc với đáy. Gọi \(R\) là bán kính mặt cầu ngoại tiếp khối chóp \(S.ABCD.\) Tỉ số \(\dfrac{R}{a}\) nhận giá trị nào sau đây ?
Đáp án: D Phương pháp giải: Lời giải chi tiết:
+ Gọi \(O\) là trung điểm \(AD \Rightarrow OA = OB = OC = OD = a\). \(\begin{array}{l} \Rightarrow {{\rm{R}}_{day}} = a\\ \Rightarrow {R_{mcnt}} = \sqrt {{a^2} + \dfrac{{{{\left( {2a} \right)}^2}}}{4}} = a\sqrt 2 \end{array}\) Chọn D. Câu hỏi 34 : Cho hình chóp \(S.ABCD\) có tất cả các cạnh đều bằng 2. Xác định bán kính mặt cầu ngoại tiếp hình chóp \(S.ABCD\).
Đáp án: C Phương pháp giải: Lời giải chi tiết: \( + \)\(\left\{ O \right\} = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\) \( + \)Xét \(\Delta ABC\)có \(\widehat {ABC} = {90^0}\) ta có:
\(A{B^2} + B{C^2} = A{C^2}\) (Định lí Pytago) \(\begin{array}{l} \Leftrightarrow {2^2} + {2^2} = A{C^2} \Leftrightarrow AC = 2\sqrt 2 \\ \Rightarrow OA = OC = OB = OD = \dfrac{{AC}}{2} = \dfrac{{2\sqrt 2 }}{2} = \sqrt 2 \end{array}\) \( + \)Xét \(\Delta SOC\) có \(\widehat {SOC} = {90^0}\): \(S{O^2} + O{C^2} = S{C^2}\)(Định lí Pytago) \( \Leftrightarrow S{O^2} = {2^2} - {\left( {\sqrt 2 } \right)^2} = 2 \Leftrightarrow SO = \sqrt 2 \) \( \Rightarrow R = \dfrac{{S{C^2}}}{{2.SO}} = \dfrac{{{2^2}}}{{2\sqrt 2 }} = \dfrac{2}{{\sqrt 2 }} = \sqrt 2 \). Chọn C Câu hỏi 35 : Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh bằng \(a.\) Diện tích mặt cầu ngoại tiếp hình chóp \(S.ABCD\) là:
Đáp án: C Phương pháp giải: Lời giải chi tiết:
\( + )\)Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\). \( + )\)Xét \(\Delta ABC\)có \(\widehat {ABC} = {90^0}\): \(A{B^2} + B{C^2} = A{C^2}\) (Định lí Pytago) \( \Leftrightarrow {a^2} + {a^2} = A{C^2} \Rightarrow AC = a\sqrt 2 \) \( \Rightarrow OA = OB = OC = OD = \dfrac{{AC}}{2} = a\dfrac{{\sqrt 2 }}{2}\) \( + )\)Xét \(\Delta SOC\) có \(\widehat {SOC} = {90^0}\): \(S{O^2} + O{C^2} = S{C^2}\) (Định lí Pytago) \( \Leftrightarrow S{O^2} = {a^2} - {\left( {\dfrac{{\sqrt 2 }}{2}a} \right)^2} \Leftrightarrow SO = \dfrac{{\sqrt 2 }}{2}a\) \(\begin{array}{l} \Rightarrow R = \dfrac{{S{C^2}}}{{2.SO}} = \dfrac{{{a^2}}}{{2.\dfrac{{\sqrt 2 }}{2}a}} = \dfrac{{\sqrt 2 }}{2}a\\ \Rightarrow S = 4\pi .{R^2} = 4\pi {\left( {\dfrac{{\sqrt 2 }}{2}a} \right)^2} = 2\pi {a^2}\end{array}\) Chọn C Câu hỏi 36 : Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(1,\) chiều cao \(SH = 2.\) Tính bán kính mặt cầu ngoại tiếp hình chóp \(S.ABCD.\)
Đáp án: A Phương pháp giải: Lời giải chi tiết:
\( + )\)Xét \(\Delta ABC\)có \(\widehat {ABC} = {90^0}\): \(A{B^2} + B{C^2} = A{C^2}\) (Định lí Pytago) \( \Leftrightarrow {1^2} + {1^2} = A{C^2} \Leftrightarrow AC = \sqrt 2 \) \( \Rightarrow HC = HA = HB = HD = \dfrac{{AC}}{2} = \dfrac{{\sqrt 2 }}{2}\) \( + )\)Xét \(\Delta SHC\)có \(\widehat {SHC} = {90^0}\): \(S{H^2} + H{C^2} = S{C^2}\) (Định lí Pytago) \( \Leftrightarrow {2^2} + {\left( {\dfrac{{\sqrt 2 }}{2}} \right)^2} = S{C^2} \Rightarrow SC = \dfrac{{3\sqrt 2 }}{2}\) \( \Rightarrow R = \dfrac{{S{C^2}}}{{2.SH}} = \dfrac{{{{\left( {\dfrac{{3\sqrt 2 }}{2}} \right)}^2}}}{{2.2}} = \dfrac{9}{8}\). Chọn A Câu hỏi 37 : Một tứ diện đều có độ dài mỗi cạnh là 2. Tính thể tích khối cầu ngoại tiếp tứ diện này.
Đáp án: A Phương pháp giải: Lời giải chi tiết:
\( + )\)\({V_{SABC}} = \dfrac{{\sqrt 2 }}{{12}}{.2^3} = \dfrac{{2\sqrt 2 }}{3}\) \( + )\) Gọi \(H\) là trọng tâm \(\Delta ABC\)\( \Rightarrow SH \bot \left( {ABC} \right)\) \( + )\)Có \({V_{SABC}} = \dfrac{1}{3}.SH.{S_{\Delta ABC}} \Leftrightarrow \dfrac{{2\sqrt 2 }}{3} = \dfrac{1}{3}.SH.\dfrac{{\sqrt 3 }}{4}{.2^2} \Rightarrow SH = \dfrac{{2\sqrt 6 }}{3}\) \( \Rightarrow R = \dfrac{{S{C^2}}}{{2.SH}} = \dfrac{{{2^2}}}{{2.\dfrac{{2\sqrt 6 }}{3}}} = \dfrac{{\sqrt 6 }}{2}\) \( \Rightarrow \)Vcầu \( = \dfrac{4}{3}\pi .{R^3} = \dfrac{4}{3}\pi .{\left( {\dfrac{{\sqrt 6 }}{2}} \right)^3} = \pi \sqrt 6 \). Chọn A Câu hỏi 38 : Cho \(a\) là một số thực dương. Một mặt cầu có diện tích bằng \(16\pi {a^2}\) thì thể tích của nó bằng :
Đáp án: B Phương pháp giải: Lời giải chi tiết: \(\begin{array}{l} + \,\,{S_{mat\,cau}} = 16\pi {a^2} \Leftrightarrow 4\pi {R^2} = 16\pi {a^2} \Leftrightarrow {R^2} = 4{a^2} \Leftrightarrow R = 2a.\\ + \,\,V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi .{\left( {2a} \right)^3} = \dfrac{{32\pi }}{3}{a^3}.\end{array}\) Chọn B Câu hỏi 39 : Một khối cầu có thể tích \(V = \dfrac{{500}}{3}\pi .\) Tính diện tích \(S\) của mặt cầu tương ứng.
Đáp án: D Phương pháp giải: Lời giải chi tiết: \(\begin{array}{l}V = \dfrac{{500}}{3}\pi \Rightarrow \dfrac{4}{3}\pi {R^3} = \dfrac{{500}}{3}\pi \Leftrightarrow {R^3} = 125 \Leftrightarrow R = 5\\ \Rightarrow {S_{mc}} = 4\pi {R^2} = 4\pi {5^2} = 100\pi .\end{array}\) Chọn D Câu hỏi 40 : Cho 2 khối cầu \(\left( {{S_1}} \right)\) có bán kính \({R_1}\), thể tích \({V_1}\) và \(\left( {{S_2}} \right)\) có bán kính \({R_2}\), thể tích \({V_2}\). Biết \({V_2} = 8{V_1}\), khẳng định nào sau đây đúng?
Đáp án: C Phương pháp giải: Lời giải chi tiết: \(\begin{array}{l}{V_1} = \dfrac{4}{3}\pi R_1^3;\,\,{V_2} = \dfrac{4}{3}\pi R_2^3\\{V_2} = 8{V_1} \Leftrightarrow \dfrac{4}{3}\pi R_2^3 = 8.\dfrac{4}{3}\pi R_1^3 \Leftrightarrow R_2^3 = 8R_1^3 \Leftrightarrow R_2^3 = {\left( {2{R_1}} \right)^3} \Leftrightarrow {R_2} = 2{R_1}\end{array}\) Chọn C Quảng cáo
|