40 bài tập trắc nghiệm mặt cầu mức độ nhận biếtLàm bàiQuảng cáo
Câu hỏi 1 : Cho khối cầu có bán kính \(R = 6\). Thể tích của khối cầu bằng
Đáp án: C Phương pháp giải: Thể tích của khối cầu có bán kính R là \(V = \dfrac{4}{3}\pi {R^3}\). Lời giải chi tiết: Thể tích của khối cầu bằng \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {.6^3} = 288\pi \). Chọn C. Câu hỏi 2 : Cho khối cầu có đường kính bằng 1. Thể tích của khối cầu đã cho bằng
Đáp án: B Phương pháp giải: Thể tích khối cầu có bán kính \(R\) là: \(V = \dfrac{4}{3}\pi {R^3}.\) Lời giải chi tiết: Bán kính khối cầu đã cho là: \(R = \dfrac{1}{2}.\) \( \Rightarrow \) Thể tích khối cầu đã cho là: \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {\left( {\dfrac{1}{2}} \right)^3} = \dfrac{\pi }{6}.\) Chọn B. Câu hỏi 3 : Cho khối cầu có bán kính bằng 2. Thể tích khối cầu đã cho bằng:
Đáp án: A Phương pháp giải: Thể tích khối cầu có bán kính \(R\) là: \(V = \dfrac{4}{3}\pi {R^3}.\) Lời giải chi tiết: Thể tích khối cầu đã cho là: \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {.2^3} = \dfrac{{32\pi }}{3}.\) Chọn A. Câu hỏi 4 : Mặt cầu có bán kính bằng 6 thì có diện tích bằng
Đáp án: B Phương pháp giải: Diện tích mặt cầu bán kính \(r\) là: \(S = 4\pi {r^2}.\) Lời giải chi tiết: Diện tích mặt cầu đã cho là:\(S = 4\pi {r^2} = 4\pi {.6^2} = 144\pi .\) Chọn B. Câu hỏi 5 : Một mặt cầu có bán kính bằng \(a.\) Diện tích của mặt cầu đó là:
Đáp án: B Phương pháp giải: Diện tích mặt cầu bán kính \(r\) là: \(S = 4\pi {r^2}.\) Lời giải chi tiết: Diện tích mặt cầu đã cho là:\(S = 4\pi {a^2}.\) Chọn B. Câu hỏi 6 : Cho khối cầu có đường kính bằng 12. Thể tích khối cầu đã cho bằng
Đáp án: D Phương pháp giải: Thể tích khối cầu bán kính \(R\) là \(V = \dfrac{4}{3}\pi {R^3}.\) Lời giải chi tiết: Bán kính của mặt cầu đã cho là:\(R = 12:2 = 6.\) Thể tích khối cầu đã cho là: \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {.6^3} = 288\pi .\) Chọn D. Câu hỏi 7 : Một mặt cầu có độ dài đường kính bằng \(4\). Tính diện tích của mặt cầu đó?
Đáp án: D Phương pháp giải: - Tính bán kính mặt cầu đó. - Áp dụng công thức tính diện tích mặt cầu bán kính r là: \(S = 4\pi {r^2}.\) Lời giải chi tiết: Mặt cầu có đường kính bằng 4 nên bán kính mặt cầu là \(r = 2\). Khi đó diện tích mặt cầu bằng \(S = 4\pi {r^2} = 4\pi {.2^2} = 16\pi .\) Chọn D. Câu hỏi 8 : Diện tích của mặt cầu bán kính R được xác định theo công thức:
Đáp án: C Phương pháp giải: Diện tích của mặt cầu bán kính R được xác định theo công thức: \(S = 4\pi {R^2}.\) Lời giải chi tiết: Diện tích của mặt cầu bán kính R được xác định theo công thức: \(S = 4\pi {R^2}.\) Chọn C. Câu hỏi 9 : Cho khối cầu có đường kính \(d = 3\). Thể tích khối cầu đã cho bằng
Đáp án: B Phương pháp giải: Áp dụng công thức tính thể tích khối cầu bán kính \(R\): \(V = \dfrac{4}{3}\pi {R^3}.\) Lời giải chi tiết: Ta có khối cầu có đường kính \(d = 3\) nên có bán kính là \(R = \dfrac{d}{2} = \dfrac{3}{2}.\) Vậy thể tích khối cầu là \(V = \dfrac{4}{3}\pi {\left( {\dfrac{3}{2}} \right)^3} = \dfrac{{9\pi }}{2}.\) Chọn B. Câu hỏi 10 : Cho mặt cầu có bán kính \(R = 3.\) Diện tích của mặt cầu đã cho bằng
Đáp án: B Phương pháp giải: Diện tích của mặt cầu bán kính R là: \(S = 4\pi {R^2}\). Lời giải chi tiết: Diện tích của mặt cầu đã cho bằng: \(S = 4\pi {R^2} = 4\pi {.3^2} = 36\pi \). Chọn B. Câu hỏi 11 : Thể tích của khối cầu bán kính r là:
Đáp án: A Phương pháp giải: Công thức tính thể của khối cầu có bán kính \(r:\;\;V = \dfrac{4}{3}\pi {r^3}.\) Lời giải chi tiết: Công thức tính thể của khối cầu có bán kính \(r:\;\;V = \dfrac{4}{3}\pi {r^3}.\) Chọn A. Câu hỏi 12 : Một mặt cầu có bán kính \(R = 4\). Diện tích mặt cầu đó bằng:
Đáp án: D Phương pháp giải: Diện tích mặt cầu bán kính \(R\) là: \({S_{mc}} = 4\pi {R^2}.\) Lời giải chi tiết: Diện tích mặt cầu đó bằng: \(S = 4\pi {.4^2} = 64\pi \). Chọn D. Câu hỏi 13 : Cho khối cầu có thể tích \(36\pi \). Bán kính của khối cầu đã cho bằng:
Đáp án: C Phương pháp giải: Thể tích khối cầu có bán kính \(R\) là: \({V_{cau}} = \dfrac{4}{3}\pi {R^3}.\) Lời giải chi tiết: Khối cầu có thể tích \(36\pi \)\( \Rightarrow \dfrac{4}{3}\pi {R^3} = 36\pi \Leftrightarrow R = 3.\) Chọn C. Câu hỏi 14 : Cho mặt cầu \(\left( S \right)\) có bán kính \(R = 2\,\,\left( {cm} \right).\) Tính diện tích \(S\) của mặt cầu.
Đáp án: C Phương pháp giải: Diện tích mặt cầu bán kính \(R\) là \(S = 4\pi {R^2}.\) Lời giải chi tiết: Diện tích của mặt cầu đã cho là \(S = 4\pi {R^2} = 4\pi {.2^2} = 16\pi \,\,\left( {c{m^2}} \right).\) Chọn C. Câu hỏi 15 : Diện tích mặt cầu có đường kính \(R\) là:
Đáp án: B Phương pháp giải: Công thức tính diện tích mặt cầu có bán kính \(r\) là: \(S = 4\pi {r^2}.\) Lời giải chi tiết: Diện tích mặt cầu có đường kính \(R\) là: \(S = 4\pi {\left( {\dfrac{R}{2}} \right)^2} = \pi {R^2}.\) Chọn B. Câu hỏi 16 : Một quả bóng đá có dạng hình cầu bán kính 12cm. Diện tích mặt ngoài quả bóng là
Đáp án: D Phương pháp giải: Diện tích khối cầu bán kính \(R\) là \(S = 4\pi {R^2}\). Lời giải chi tiết: Diện tích mặt ngoài của quả bóng dạng hình cầu bán kính \(12\,\,cm\) là \(S = 4\pi {.12^2} = 576\pi \,\,\left( {c{m^2}} \right)\). Chọn D. Câu hỏi 17 : Thể tích của khối cầu đường kính 3R bằng:
Đáp án: C Phương pháp giải: Công thức tính thể của khối cầu có bán kính \(r:\;\;V = \dfrac{4}{3}\pi {r^3}.\) Lời giải chi tiết: Bán kính khối cầu là: \(r = \dfrac{{3R}}{2}.\) Thể tích của khối cầu là:\(V = \dfrac{4}{3}\pi {r^3} = \dfrac{4}{3}\pi {\left( {\dfrac{{3R}}{2}} \right)^3} = \dfrac{{9\pi {R^3}}}{2}.\) Chọn C. Câu hỏi 18 : Thể tích của khối cầu có bán kính \(6cm\) là
Đáp án: B Phương pháp giải: Thể tích của khối cầu có cạnh bằng \(a\) là \(V = \dfrac{4}{3}\pi {a^3}\) Lời giải chi tiết: Thể tích của khối cầu có bán kính \(6cm\) là : \(V = \dfrac{4}{3}\pi {.6^3} = 288\pi \left( {c{m^3}} \right)\) Chọn B Câu hỏi 19 : Một quả bóng bàn có mặt ngoài là mặt cầu đường kính \(4cm.\) Diện tích mặt ngoài quả bóng bàn là
Đáp án: C Phương pháp giải: Diện tích mặt cầu bán kính \(R\) là \(S = 4\pi {R^2}\). Lời giải chi tiết: Quả bóng bàn có đường kính 4cm nên có bán kính \(R = 2cm\). Vậy diện tích mặt cầu là \(S = 4\pi {R^2} = 4\pi {.2^2} = 16\pi \,\,\left( {c{m^2}} \right)\). Đáp án C. Câu hỏi 20 : Tính bán kính của khối cầu có thể tích bằng \(36\pi \left( {c{m^3}} \right)\)?
Đáp án: B Phương pháp giải: Công thức tính thể tích của khối cầu : \(V = \dfrac{4}{3}\pi {R^3}\), \(R\) là bàn kính của khối cầu. Lời giải chi tiết: \(V = \dfrac{4}{3}\pi {R^3} \Leftrightarrow 36\pi = \dfrac{4}{3}\pi {R^3} \Leftrightarrow R = 3\,\,\left( {cm} \right)\) Vậy bán kính của khối cầu đã cho là \(3\left( {cm} \right).\) Chọn B. Câu hỏi 21 : Thể tích của khối cầu có bán kính \(r = 2\) là :
Đáp án: A Phương pháp giải: Sử dụng công thức tính thể tích khối cầu bán kính \(R\) là \(V = \dfrac{4}{3}\pi {R^3}\) Lời giải chi tiết: Thể tích khối cầu là: \(V = \dfrac{4}{3}\pi {r^3} = \dfrac{4}{3}\pi {.2^3} = \dfrac{{32}}{3}\pi \) Chọn A Câu hỏi 22 : Nếu một mặt cầu có đường kính bằng \(a\) thì có diện tích bằng:
Đáp án: A Phương pháp giải: Công thức tính diện tích mặt cầu bán kính \(R:\,\,S = 4\pi {R^2}.\) Lời giải chi tiết: Bán kính của mặt cầu là:\(r = \frac{a}{2}.\) \( \Rightarrow \) Diện tích mặt cầu đã cho là: \(S = 4\pi .{\left( {\frac{a}{2}} \right)^2} = \pi {a^2}.\) Chọn A. Câu hỏi 23 : Cho mặt cầu tâm \(O\) đường kính 9cm. Mặt phẳng \(\left( P \right)\) tiếp xúc với mặt cầu đã cho khi và chỉ khi khoảng cách từ \(O\) đến \(\left( P \right)\) bằng:
Đáp án: B Phương pháp giải: \(\left( P \right)\) tiếp xúc với mặt cầu \(\left( S \right)\) tâm \(I\), bán kính \(R \Leftrightarrow d\left( {I;\left( P \right)} \right) = R\). Lời giải chi tiết: Mặt cầu tâm \(O\) có đường kính \(9cm \Rightarrow \) Bán kính \(R = \frac{9}{2} = 4,5\,\,\left( {cm} \right)\). Vì mặt cầu tâm \(\left( P \right)\) tiếp xúc với mặt phẳng \(\left( P \right)\) nên \(d\left( {O;\left( P \right)} \right) = R = 4,5\,\,\left( {cm} \right)\). Chọn B. Câu hỏi 24 : Một khối cầu có bán kính \(2R\) thì có thể tích \(V\) bằng bao nhiêu?
Đáp án: C Phương pháp giải: Lời giải chi tiết: \(V = \dfrac{4}{3}\pi .{\left( {2R} \right)^3} = \dfrac{{32\pi }}{3}.{R^3}\) Chọn C Câu hỏi 25 : Cho hai khối cầu \({S_1}\) và \({S_2}\) có bán kính và thể tích lần lượt là \({R_1},\,\,{R_2}\) và \({V_1},\,\,{V_2}\). Biết \({R_2} = \sqrt 3 {R_1}\), tính \(\dfrac{{{V_2}}}{{{V_1}}}\).
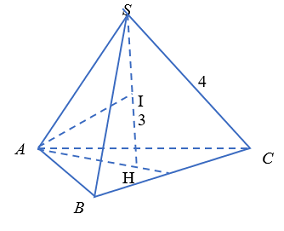
Đáp án: D Phương pháp giải: Lời giải chi tiết: \(\begin{array}{l}{V_1} = \dfrac{4}{3}\pi R_1^3;\,\,\,\,{V_2} = \dfrac{4}{3}\pi R_2^3\\ \Rightarrow \dfrac{{{V_2}}}{{{V_1}}} = \dfrac{{\dfrac{4}{3}\pi R_2^3}}{{\dfrac{4}{3}\pi R_1^3}} = \dfrac{{R_2^3}}{{R_1^3}} = \dfrac{{{{\left( {\sqrt 3 {R_1}} \right)}^3}}}{{R_1^3}} = 3\sqrt 3 \end{array}\) Chọn D Câu hỏi 26 : Cho hình chóp \(S.ABC\) có \(SA = SB = SC = 4\), đường cao \(SH = 3\). Tính bán kính \(r\) của mặt cầu ngoại tiếp hình chóp\(S.ABC\).
Đáp án: C Phương pháp giải: Lời giải chi tiết:
\({R_{mcnt}} = \dfrac{{S{A^2}}}{{2.SH}} = \dfrac{{{4^2}}}{{2.3}} = \dfrac{8}{3}\) Chọn C Câu hỏi 27 : Tính diện tích \(S\) của mặt cầu có đường kính bằng \(6\).
Đáp án: B Phương pháp giải: Công thức diện tích mặt cầu bán kính \(R\) là \(S = 4\pi {R^2}\). Lời giải chi tiết: Diện tích mặt cầu là \(S = 4\pi .{\left( {\dfrac{6}{2}} \right)^2} = 36\pi \). Chọn B Câu hỏi 28 : Diện tích của mặt cầu đường kính 2a bằng
Đáp án: C Phương pháp giải: Diện tích mặt cầu có bán kính r là \(4\pi {r^2}\). Lời giải chi tiết: Diện tích của mặt cầu đường kính 2a bằng \(4\pi {\left( {\dfrac{{2a}}{2}} \right)^2} = 4\pi {a^2}\). Chọn: C Câu hỏi 29 : Hình cầu có đường kính bằng 2 thì thể tích bằng
Đáp án: B Phương pháp giải: Thể tích hình cầu bán kính \(R\) là \(V = \frac{4}{3}\pi {R^3}\) Lời giải chi tiết: Bán kính hình cầu là \(R = \frac{d}{2} = \frac{2}{2} = 1\) Thể tích hình cầu là \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi \) Chọn B. Câu hỏi 30 : Tính đường kính mặt cầu ngoại tiếp hình lập phương có cạnh bằng \(a\sqrt 3 \).
Đáp án: A Phương pháp giải: - Mặt cầu ngoại tiếp hình lập phương có đường kính là đường chéo chính của hình lập phương. - Hình lập phương cạnh \(a\) có độ dài đường chéo chính là \(a\sqrt 3 \). Lời giải chi tiết: Đường kính mặt cầu ngoại tiếp hình lập phương cạnh \(a\sqrt 3 \) là \(a\sqrt 3 .\sqrt 3 = 3a\). Chọn A Câu hỏi 31 : Diện tích hình cầu bán kính \(a\sqrt 3 \) là
Đáp án: C Phương pháp giải: Lời giải chi tiết: Chọn C. Câu hỏi 32 : Tính thể tích khối cầu có đường kính \(2a\).
Đáp án: C Phương pháp giải: Khối cầu có bán kính \(R\) thì có thể tích \(V = \frac{4}{3}\pi {R^3}\) Lời giải chi tiết: Bán kính mặt cầu là \(R = 2a:2 = a\) Thể tích khối cầu là \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {a^3}.\) Chọn C. Câu hỏi 33 : Diện tích của mặt cầu có đường kính 3m là:
Đáp án: A Phương pháp giải: Diện tích của mặt cầu có bán kính R là: \(4\pi {R^2}\). Lời giải chi tiết: Diện tích của mặt cầu có đường kính 3m là: \(4\pi {\left( {\dfrac{3}{2}} \right)^2} = \)\(9\pi \left( {{m^2}} \right)\). Chọn: A Câu hỏi 34 : Một quả bóng đá có dạng hình cầu bán kính 12cm. Diện tích mặt ngoài quả bóng là
Đáp án: C Phương pháp giải: Công thức tính diện tích mặt cầu bán kính \(R:\;\;S = 4\pi {R^2}.\) Lời giải chi tiết: Ta có: \(S = 4\pi {R^2} = 4\pi {.12^2} = 576\pi \,\,\left( {c{m^2}} \right).\) Chọn C. Câu hỏi 35 : Tính diện tích S của mặt cầu và thể tích V của khối cầu có bán kính bằng 3cm.
Đáp án: A Phương pháp giải: Diện tích mặt cầu bán kính R là: \(S = 4\pi {R^2}\) Thể tích mặt cầu bán kính R là: \(V = \dfrac{4}{3}\pi {R^3}\) Lời giải chi tiết: Diện tích mặt cầu đó là: \(S = 4\pi {.3^2} = 36\pi \left( {c{m^2}} \right)\) Thể tích mặt cầu đó là: \(V = \dfrac{4}{3}\pi {.3^3} = 36\pi \left( {c{m^3}} \right)\) Chọn: A Câu hỏi 36 : Thể tích khối cầu có bán kính bằng \(\frac{a}{2}\) là:
Đáp án: C Phương pháp giải: Công thức tính thể tích khối cầu có bán kính \(r\) là: \(V = \frac{4}{3}\pi {r^3}\). Lời giải chi tiết: Thể tích khối cầu có bán kính bằng \(\frac{a}{2}\) là: \(V = \frac{4}{3}\pi {\left( {\frac{a}{2}} \right)^3} = \)\(\frac{{\pi {a^3}}}{6}\). Chọn: C Câu hỏi 37 : Tính diện tích của mặt cầu có bán kính \(r = 2\)
Đáp án: D Phương pháp giải: Công thức tính diện tích mặt cầu bán kính \(R:\;\;S = 4\pi {R^2}.\) Lời giải chi tiết: Công thức tính diện tích mặt cầu bán kính \(r = \;2:\;\;S = 4\pi {.2^2} = 16\pi .\) Chọn D. Câu hỏi 38 : Một mặt cầu có diện tích xung quanh là \(\pi \) thì có bán kính bằng
Đáp án: C Phương pháp giải: Công thức tính diện tích mặt cầu bán kính \(R\) là: \(S = 4\pi {R^2}\). Lời giải chi tiết: Ta có: \(S = \pi = 4\pi {R^2} \Leftrightarrow {R^2} = \dfrac{1}{4} \Leftrightarrow R = \dfrac{1}{2}\). Chọn C. Câu hỏi 39 : Một khối cầu có đường kính bằng \(2\sqrt 3 \) có thể tích bằng:
Đáp án: C Phương pháp giải: Sử dụng công thức tính thể tích khối cầu \(V = \frac{4}{3}\pi {R^3}\) trong đó R là bán kính khối cầu. Lời giải chi tiết: Thể tích khối cầu là \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {\frac{{2\sqrt 3 }}{2}} \right)^3} = 4\sqrt 3 \pi \). Chọn C. Câu hỏi 40 : Tập hợp tâm các mặt cầu đi qua ba điểm phân biệt không thẳng hàng là :
Đáp án: B Phương pháp giải: Tập hợp tâm các mặt cầu đi qua ba điểm phân biệt A, B, C không thẳng hàng là trục của đường tròn ngoại tiếp tam giác ABC. Lời giải chi tiết: Tập hợp tâm các mặt cầu đi qua ba điểm phân biệt A, B, C không thẳng hàng là trục của đường tròn ngoại tiếp tam giác ABC. Chọn B. Quảng cáo
|