40 bài tập đường thẳng song song với mặt phẳng mức độ thông hiểuLàm bàiQuảng cáo
Câu hỏi 1 : Trong các mệnh đề sau đây mệnh đề nào đúng?
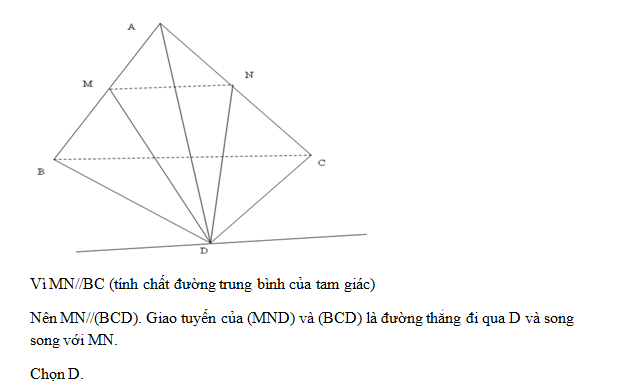
Đáp án: D Phương pháp giải: Lời giải chi tiết: A sai, vì có thể hai đường thẳng cắt nhau. B sai, vì có thể đường thẳng nằm trên mặt phẳng đó. C sai, vì có thể hai đường thẳng đó chéo nhau. D đúng Chọn D. Câu hỏi 2 : Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB và AC. Khi đó giao tuyến của (DMN) và (DBC) là:
Đáp án: D Phương pháp giải: Lời giải chi tiết:
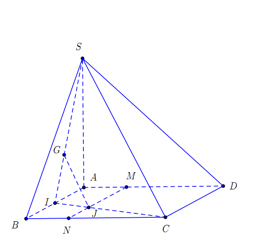
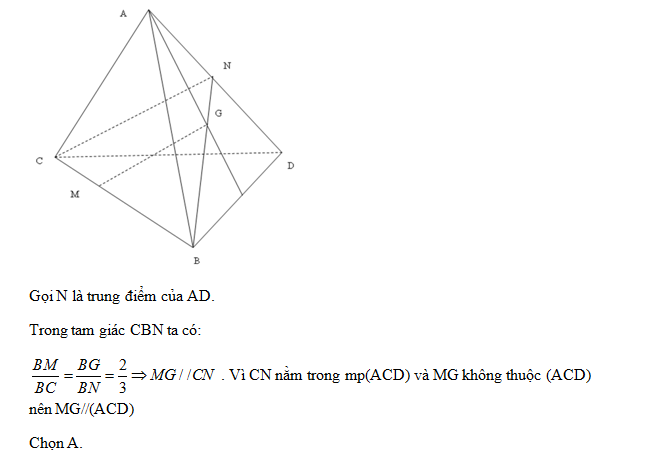
Câu hỏi 3 : Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD. Trên đoạn BC lấy điểm M sao cho MB=2MC. Khi đó
Đáp án: A Phương pháp giải: Lời giải chi tiết:
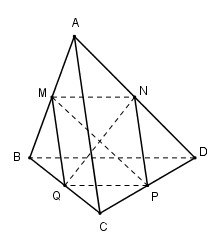
Câu hỏi 4 : Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, AD, CD, BC. Mệnh đề nào sau đây là sai ?
Đáp án: A Phương pháp giải: - Đưa về cùng mặt phẳng. - Sử dụng các tính chất đường trung bình của tam giác. Lời giải chi tiết:
Ta có: MN, PQ lần lượt là đường trung bình của tam giác ABD và CBD nên MN // BD ; \(MN = {1 \over 2}BD\) và PQ // BD ; \(PQ = {1 \over 2}BD\) \( \Rightarrow \) MN // PQ và MN = PQ. Do đó MNPQ là hình bình hành. Vậy A sai. Chọn A. Câu hỏi 5 : Mệnh đề nào dưới đây đúng?
Đáp án: C Phương pháp giải: Sử dụng các kiến thức về đường thẳng song song với đường thẳng và đường thẳng song song với mặt phẳng. Lời giải chi tiết: A và D sai vì hai đường thẳng cùng song song với một mặt phẳng thì hai đường thẳng đó song song với nhau hoặc trùng nhau. Chọn C. Câu hỏi 6 : Cho các mệnh đề sau: a. Nếu a // (P) thì a song song với mọi đường thẳng nằm trong (P). b. Nếu a // (P) thì a song song với một đường thẳng nào đó nằm trong (P). c. Nếu a // (P) thì có vô số đường thẳng nằm trong (P) và song song với a. d. Nếu a // (P) thì có một đường thẳng d nào đó nằm trong (P) sao cho a và d đồng phẳng. Số mệnh đề đúng trong các mệnh đề trên là:
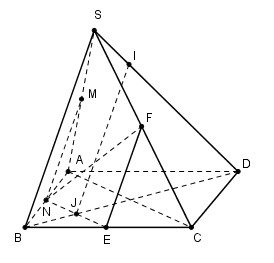
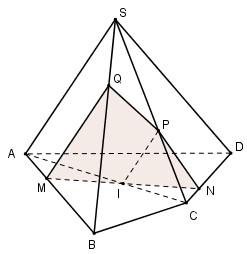
Đáp án: C Phương pháp giải: Vận dụng các kiến thức về đường thẳng song song với mặt phẳng. Lời giải chi tiết: Các mệnh đề b, c, d đúng. Chọn C. Câu hỏi 7 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD và BD tại M, N, E, F, I, J. Xét các khẳng định sau: (1) MN // (SCD) (2) EF // (SAD) (3) NE // (SAC) (3) IJ // (SAB) Có bao nhiêu khẳng định đúng?
Đáp án: B Phương pháp giải: - Đưa về cùng mặt phẳng - Chứng minh đường thẳng song song với mặt phẳng a // b a // (P). Lời giải chi tiết:
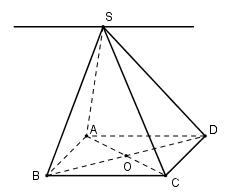
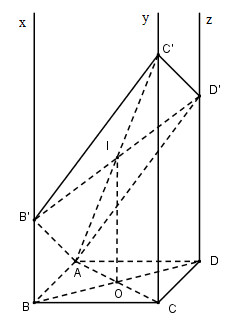
Trước hết ta lấy điểm \(M \in \left( P \right)\) sao cho \(M \in SA\). Trong mp(SAB) kẻ MN // SA \(\left( {N \in AB} \right)\), trong mp(ABCD) kẻ NE // AC \(\left( {E \in BC} \right)\). \(NE \cap BD = \left\{ J \right\}\) Trong mp(SBC) kẻ EF // SB \(\left( {F \in SC} \right)\), trong mp(SBD) kẻ JI // SD \(\left( {I \in SD} \right)\). Giả sử MN // (SCD) Lại có: MN // SB \( \Rightarrow SB \subset \left( {SCD} \right)\)(vô lý) nên (1) sai. Tương tự ta chứng minh được (2) sai. NE // AC \( \subset \left( {SAC} \right) \Rightarrow \)NE // (SAC). Do đó (3) đúng. IJ // SB \( \subset \left( {SAB} \right) \Rightarrow \)IJ // (SAB). Do đó (4) đúng. Chọn B. Câu hỏi 8 : Cho hình bình hành ABCD. Gọi Bx, Cy, Dz là các đường thẳng song song với nhau lần lượt đi qua B, C, D và nằm về một phía của mặt phẳng (ABCD), đồng thời không nằm trong mặt phẳng (ABCD). Một mặt phẳng đi qua A và cắt Bx, Cy, Dz lần lượt tại các điểm B’, C’, D’ với BB’ = 2, DD’ = 4. Khi đó CC’ bằng:
Đáp án: D Phương pháp giải: - Đưa về cùng mặt phẳng; - Sử dụng các tính chất của đường trung bình của tam giác, đường trung bình của hình thang. Lời giải chi tiết:
Trên Cx và Dy lấy điểm B’ và D’ sao cho BB’ = 2, DD’ = 4. Gọi O là tâm hình bình hành ABCD, I là trung điểm của B’D’ \(I \in B'D'\) Ta có BDD’B’ là hình thang, OI là đường trung bình của hình thang nên OI // BB’ // DD’ // Cz và \(OI = {{BB' + {\rm{DD}}'} \over 2} = {{2 + 4} \over 2} = 3\). Xét mặt phẳng tạo bởi OI và CC’ có: \(AI \cap Cz = C'\). Ta có OI // CC’, AO = OC suy ra AI = IC’ Suy ra OI là đường trung bình của tam giác ACC’ \( \Rightarrow CC' = 2OI = 6\) Chọn D. Câu hỏi 9 : Trong các mệnh đề sau, mệnh đề nào đúng?
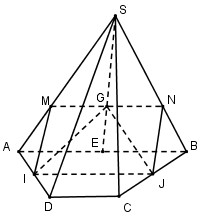
Đáp án: A Phương pháp giải: Lời giải chi tiết: B sai vì hai đường thẳng phân biệt không cắt nhau thì có thể chéo nhau hoặc song song. C sai vì hai đường thẳng phân biệt không song song thì có thể chéo nhau hoặc cắt nhau. D sai vì hai đường thẳng phân biệt lần lượt thuộc hai mặt phẳng khác nhau thì chéo nhau hoặc song song. Chọn A. Câu hỏi 10 : Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi I, J lần lượt là trung điểm của các cạnh AD và BC và G là trọng tâm tam giác SAB. Tìm giao tuyến của hai mặt phẳng (SAB) và (IJG)
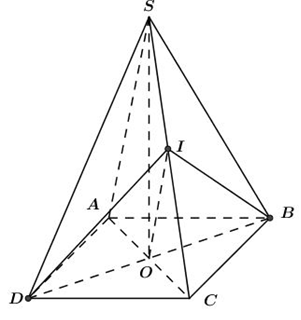
Đáp án: D Phương pháp giải: - Sử dụng tính chất: Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) có điểm chung M và lần lượt chứa hai đường thẳng song song d và d’ thì giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) là đường thẳng đi qua M và song song với d và d’. Lời giải chi tiết:
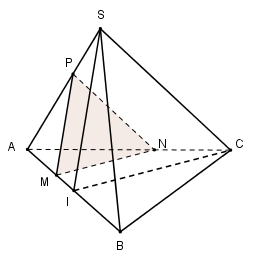
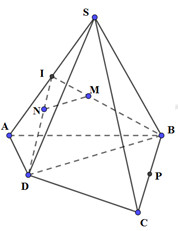
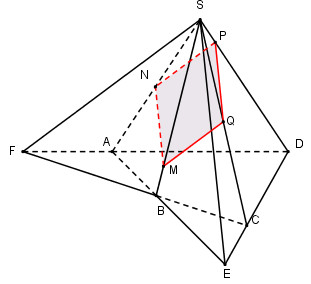
Ta có: ABCD là hình thang và I, J là trung điểm của AD và BC nên IJ là đường trung bình của hình thang ABCD. \( \Rightarrow \) IJ // AB // CD. \(\left\{ \matrix{ G \in \left( {SAB} \right) \cap \left( {{\rm{IJ}}G} \right) \hfill \cr AB \subset \left( {SAB} \right) \hfill \cr {\rm{IJ}} \subset \left( {{\rm{IJ}}G} \right) \hfill \cr AB//{\rm{IJ}} \hfill \cr} \right. \Rightarrow \) Trong (SAB) qua G kẻ MN // AB \(\left( {M \in SA;N \in SB} \right)\). \( \Rightarrow \left( {SAB} \right) \cap \left( {{\rm{IJ}}G} \right) = MN\) và MN // IJ // AB // CD. Chọn D. Câu hỏi 11 : Cho chóp tứ giác S.ABCD có hai đường chéo AC và BD. Gọi E và F lần lượt là giao điểm của AB và CD, AD và BC. Một mặt phẳng \(\left( \alpha \right)\) đi qua điểm M trên cạnh SB (M nằm giữa S và B) song song với SE và SF (SE không vuông góc với SF). Thiết diện của hình chóp cắt bởi \(mp\left( \alpha \right)\) có số cạnh là:
Đáp án: B Phương pháp giải: - Đưa về cùng mặt phẳng. - Sử dụng các yếu tố song song. - Xác định thiết diện của hình chóp dựa vào các yếu tố song song. Lời giải chi tiết:
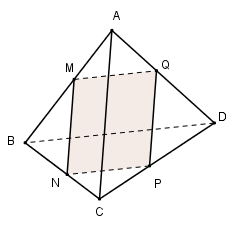
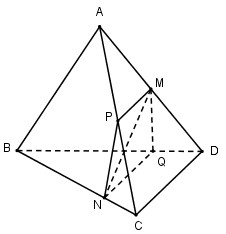
Giả sử thiết diện cần tìm đi qua điểm \(M \in SB.\) Trong (SAB) qua M kẻ MN // SE \(\left( {N \in SA} \right)\) ta có: \(\left( \alpha \right)\) và (SAB) có điểm M chung. \(\eqalign{ & \left( \alpha \right)//SE \subset \left( {SAB} \right) \cr & MN//SE \cr & \Rightarrow \left( \alpha \right) \cap \left( {SAB} \right) = MN. \cr} \) Tương tự trong (SAD) qua N kẻ NP // SF \(\left( {P \in SD} \right)\) ta có: \(\left( \alpha \right) \cap \left( {SAD} \right) = NP.\) Trong (SCD) kẻ PQ // SE \(\left( {Q \in SC} \right)\) ta có: \(\left( \alpha \right) \cap \left( {SCD} \right) = PQ.\) \(\left( \alpha \right) \cap \left( {SBC} \right) = MQ.\) Vậy thiết diện của hình chóp khi cắt bởi \(mp\left( \alpha \right)\) là tứ giác MNPQ. Chọn B. Câu hỏi 12 : Cho tứ diện ABCD. Trên cạnh AD lấy trung điểm M, trên cạnh BC lấy điểm N bất kỳ. Gọi \(\left( \alpha \right)\) là mặt phẳng chứa đường thẳng MN và song song với CD. Xác định vị trí của điểm N trên cạnh CD sao cho thiết diện là hình bình hành.
Đáp án: A Phương pháp giải: - Đưa về cùng mặt phẳng. - Xác định thiết diện dựa vào các yếu tố song song. - Sử dụng tính chất: Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) có điểm chung M và lần lượt chứa hai đường thẳng song song d và d’ thì giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) là đường thẳng đi qua M và song song với d và d’. - Sử dụng các tính chất đường trung bình của tam giác. - Vận dụng các dấu hiệu nhận biết hình thang, hình bình hành. Lời giải chi tiết:
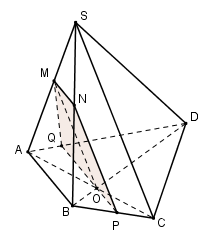
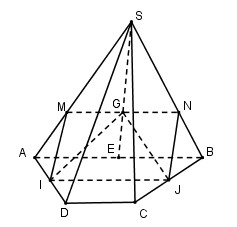
\(\left\{ \matrix{ M \in \left( \alpha \right) \cap \left( {ACD} \right) \hfill \cr CD\parallel \left( \alpha \right) \hfill \cr CD \subset \left( {ACD} \right) \hfill \cr} \right.\) Suy ra MP // CD với \(P \in CD\) Tương tự \(\left\{ \matrix{ N \in \left( \alpha \right) \cap \left( {BCD} \right) \hfill \cr CD\parallel \left( \alpha \right) \hfill \cr CD \subset \left( {BCD} \right) \hfill \cr} \right.\) Suy ra NQ // CD \(\left( {Q \in BD.} \right)\) Vậy thiết diện là tứ giác MPNQ có MP // NQ // CD nên MPNQ là hình thang. Để MPNQ là hình bình hành thì cần thêm điều kiện MP = NQ. Mà \(MP = {1 \over 2}CD\) (do MP là đường trung bình của tam giác ACD). Suy ra \(NQ = {1 \over 2}CD\). Mà NQ // CD nên NQ là đường trung bình của tam giác BCD. Vậy N là trung điểm của BC hay \(NB = {1 \over 2}BC\). Chọn A. Câu hỏi 13 : Cho hình chóp SABCD có đáy ABCD là hình vuông tâm O, tam giác SBD cân tại S. Gọi M là điểm tùy ý trên AO. Mặt phẳng \(\left( \alpha \right)\) đi qua M và song song với SA, BD cắt SO, SB, AB tại N, P, Q. Tứ giác MNPQ là hình gì?
Đáp án: C Phương pháp giải: - Dựa vào tính chất: Nếu hai mặt phẳng \(\left( \alpha \right) \) và \(\left( \beta \right)\) có điểm chung M và lần lượt chứa hai đường thẳng song song d và d’ thì giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) là đường thẳng đi qua M và song song với d và d’ để xác định thiết diện của hình chóp. - Sử dụng các tính chất về đường cao, đường trung tuyến trong tam giác cân. - Vận dụng các dấu hiệu nhận biết hình bình hành và hình chữ nhật. Lời giải chi tiết:
Tam giác SBD cân tại S nên SB = SD. Suy ra \(\Delta SBC = \Delta SDC\left( {c.c.c} \right) \Rightarrow \widehat {SCB} = \widehat {SCD}\). Gọi I là trung điểm của SC. Xét hai tam giác IBC và ICD có: IC chung BC = DC (ABCD là hình vuông) \(\widehat {ICB} = \widehat {ICD}\,\left( {cmt} \right)\) Do đó \(\Delta IBC = \Delta IDC\left( {c.g.c} \right) \Rightarrow IB = ID\) hay tam giác \(IBD\) cân tại \(I\). Do O là trung điểm của BD nên IO là đường trung tuyến trong tam giác cân \( \Rightarrow IO \bot BD.\) Mà SA // IO nên \(SA \bot BD.\) Ta có: \(\left\{ \matrix{ M \in \left( \alpha \right) \cap \left( {ABCD} \right) \hfill \cr BD\parallel \left( \alpha \right) \hfill \cr BD \subset \left( {ABCD} \right) \hfill \cr} \right.\) Suy ra giao tuyến của \(\left( \alpha \right)\) với (ABCD) là đường thẳng qua M và song song với BD cắt AB tại Q \( \Rightarrow MQ\parallel BD.\,\,\left( 1 \right)\) Ta có: \(\left\{ \matrix{ Q \in \left( \alpha \right) \cap \left( {SAB} \right) \hfill \cr SA\parallel \left( \alpha \right) \hfill \cr SA \subset \left( {SAB} \right) \hfill \cr} \right.\) suy ra giao tuyến của \(\left( \alpha \right)\) với (SAB) là đường thẳng đi qua Q và song song với SA cắt SB tại P. Do đó QP // SA (2). Ta có: \(\left\{ \matrix{ P \in \left( \alpha \right) \cap \left( {SBD} \right) \hfill \cr BD\parallel \left( \alpha \right) \hfill \cr BD \subset \left( {SBD} \right) \hfill \cr} \right.\) suy ra giao tuyến của \(\left( \alpha \right)\) với (SBD) là đường thẳng đi qua P và song song với BD cắt SO tại N. Do đó PN // BD (3). Ta có: \(\left\{ \matrix{ \left( \alpha \right) \cap \left( {SAC} \right) = MN \hfill \cr SA\parallel \left( \alpha \right) \hfill \cr SA \subset \left( {SAC} \right) \hfill \cr} \right. \Rightarrow MN\parallel SA.\) (4). Từ (1) và (3) suy ra PN // MQ // BD, từ (2) và (4) suy ra QP // MN // SA. Do đó MNPQ là hình bình hành. Lại có \(SA \bot BD \Rightarrow MN \bot MQ\). Vậy MNPQ là hình chữ nhật. Chọn C. Câu hỏi 14 : Cho hình chóp S.ABCD. Gọi M, N là hai điểm lần lượt thuộc cạnh AB và CD; là mặt phẳng đi qua MN và song song với SA. Tìm điều kiện của MN để thiết diện của hình chóp khi cắt bởi mp là một hình thang.
Đáp án: B Phương pháp giải: - Xác định thiết diện dựa vào yếu tố song song với SA. - Để một tứ giác trở thành hình thang cần thêm điều kiện một cặp cạnh đối song song. Lời giải chi tiết:
Ta có: \(\left\{ \matrix{M \in \left( \alpha \right) \cap \left( {SAB} \right) \hfill \cr \left( \alpha \right)\parallel SA \hfill \cr SA \subset \left( {SAB} \right) \hfill \cr} \right. \Rightarrow \left( {SAB} \right) \cap \left( \alpha \right) = MQ\parallel SA\,\,\left( {Q \in SB} \right).\) Trong (ABCD), gọi \(I = MN \cap AC\). Ta có: \(\eqalign{ & I \in MN,\,MN \subset \left( \alpha \right) \Rightarrow I \in \left( \alpha \right). \cr & I \in AC,\,AC \subset \left( {SAC} \right) \Rightarrow T \in \left( {SAC} \right) \cr & \Rightarrow I \in \left( \alpha \right) \cap \left( {SAC} \right). \cr}\) Vậy \(\left\{ \matrix{ I \in \left( \alpha \right) \cap \left( {SAC} \right) \hfill \cr \left( \alpha \right)\parallel SA \hfill \cr SA \subset \left( {SAC} \right) \hfill \cr} \right. \Rightarrow \left( {SAC} \right) \cap \left( \alpha \right) = IP\parallel SA\,\,\left( {P \in SC} \right).\) Thiết diện là tứ giác MNPQ. Để tứ giác MNPQ là hình thang thì cần MQ // NP hoặc MN // PQ. Trường hợp 1: Nếu MQ // NP thì Ta có: \(\left\{ \matrix{ MQ\parallel NP \hfill \cr MQ\parallel SA \hfill \cr} \right. \Rightarrow SA\parallel NP,\) mà \(NP \subset \left( {SCD} \right) \Rightarrow SA\parallel \left( {SCD} \right)\) (Vô lí). Trường hợp 2: Nếu MN // PQ thì ta có các mặt phẳng (ABCD), \(\left( \alpha \right),\) (SBC) đôi một cắt nhau theo ba giao tuyến là MN, BC, PQ nên MN // BC. Đảo lại nếu MN // BC thì \(\left\{ \matrix{ PQ = \left( \alpha \right) \cap \left( {SBC} \right) \hfill \cr MN \subset \left( \alpha \right) \hfill \cr BC \subset \left( {SBC} \right) \hfill \cr} \right. \Rightarrow PQ\parallel MN\parallel BC\) nên tứ giác MNPQ là hình thang. Vậy tứ giác MNPQ là hình thang thì điều kiện là MN // BC. Chọn B. Câu hỏi 15 : Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi I, J lần lượt là trung điểm của các cạnh AD và BC và G là trọng tâm tam giác SAB. Tìm điều kiện của AB và CD để thiết diện của (IJG) và hình chóp là một hình bình hành.
Đáp án: D Phương pháp giải: - Sử dụng tính chất: Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) có điểm chung M và lần lượt chứa hai đường thẳng song song d và d’ thì giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) là đường thẳng đi qua M và song song với d và d’. - Sử dụng các tính chất của đường trung bình của hình thang. - Sử dụng tính chất của trọng tâm tam giác. - Sử dụng định lí Ta-let để suy ra các tỉ lệ. - Dấu hiệu nhận biết các tứ giác đặc biệt. Lời giải chi tiết:
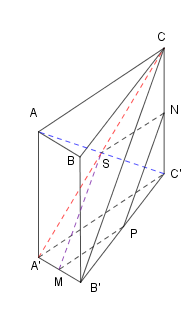
Ta có: ABCD là hình thang và I, J là trung điểm của AD và BC nên IJ là đường trung bình của hình thang ABCD. \( \Rightarrow \) IJ // AB // CD. \(\left\{ \matrix{ G \in \left( {SAB} \right) \cap \left( {{\rm{IJ}}G} \right) \hfill \cr AB \subset \left( {SAB} \right) \hfill \cr {\rm{IJ}} \subset \left( {{\rm{IJ}}G} \right) \hfill \cr AB//{\rm{IJ}} \hfill \cr} \right. \Rightarrow \) Trong (SAB) qua G kẻ MN // AB \(\left( {M \in SA;N \in SB} \right)\) \( \Rightarrow \left( {SAB} \right) \cap \left( {{\rm{IJ}}G} \right) = MN.\) và MN // IJ // AB // CD. Dễ thấy thiết diện của (IJG) và hình chóp là hình thang MNJI. G là trọng tâm của tam giác SAB và MN // AB nên theo định lí Ta-let ta có: \({{MN} \over {AB}} = {{SG} \over {SE}} = {2 \over 3}\) (Với E là trung điểm của AB). \( \Rightarrow MN = {2 \over 3}AB\) Lại có: IJ là đường trung bình của hình thang ABCD nên \({\rm{IJ}} = {{AB + CD} \over 2}.\) Để hình thang MNJI trở thành hình bình hành thì cần điều kiện MN = IJ. \( \Rightarrow {2 \over 3}AB = {1 \over 2}\left( {AB + CD} \right) \Leftrightarrow {1 \over 6}AB = {1 \over 2}CD \Leftrightarrow AB = 3CD.\) Chọn D. Câu hỏi 16 : Cho lăng trụ \(ABC.A'B'C'.\) Gọi \(M,N\) lần lượt là trung điểm của \(A'B'\) và \(CC'.\) Khi đó \(CB'\) song song với
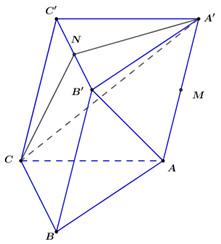
Đáp án: D Phương pháp giải: Phương pháp. Gọi \(P\) là trung điểm của \(B'C'.\)Chứng minh \(NP//\left( AMC' \right)\)và \(NP//B'C\) để suy ra \(B'C//\left( AMC' \right).\) Lời giải chi tiết: Lời giải chi tiết.
Giả sử \(S=AC'\cap A'C.\) Khi đó \(S\) là trung điểm của \(A'C.\) Vì \(SN\) là đường trung bình của \(\Delta A'C'C\)nên \(SN//A'C',\,SN=\frac{1}{2}A'C'\,\,\left( 1 \right).\) Vì \(MP\) là đường trung bình của \(\Delta A'B'C'\)nên \(MP//A'C',\,MP=\frac{1}{2}A'C'\,\,\left( 2 \right).\) Từ \(\left( 1 \right),\,\left( 2 \right)\) ta nhận được \(SN//MP,\,SN=MP.\) Do đó \(MPNS\) là hình bình hành. Kéo theo \(NP//MS.\) Vì \(MS\in \left( AMC' \right)\Rightarrow NP//\left( AMC' \right)\,\,\left( 3 \right).\) Vì \(NP\) là đường trung bình của \(\Delta B'C'C\) nên \(NP//B'C\,\,\left( 4 \right).\) Từ \(\left( 3 \right),\,\left( 4 \right)\) suy ra \(B'C//\left( AMC' \right).\) Chọn đáp án D. Câu hỏi 17 : Cho tứ diện đều SABC. Gọi I là trung điểm của AB, M là một điểm di động trên đoạn AI. Gọi (P) là mặt phẳng qua M và song song với (SIC). Thiết diện tạo bởi (P) và tứ diện S.ABC là:
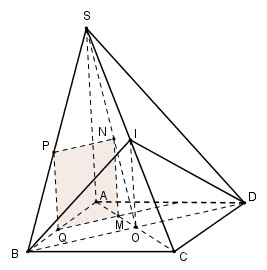
Đáp án: C Phương pháp giải: - Tìm thiết diện dựa vào các yếu tố song song để dựng thiết diện và nhận thấy thiết diện là tam giác - Sử dụng định lí Ta-let đảo để suy ra các đoạn thẳng tỉ lệ. - Tính độ dài các cạnh của tam giác. Lời giải chi tiết: Trong (ABC) qua M kẻ đường thẳng song song với CI cắt AC tại N \(\Rightarrow \left( \alpha \right)\cap \left( ABC \right)=MN\). Trong (SAB) qua M kẻ đường thẳng song song với SI cắt SA tại P \(\Rightarrow \left( \alpha \right)\cap \left( SAB \right)=MP.\) \(\Rightarrow \left( \alpha \right)\cap \left( SAC \right)=NP\) và NP // SC. Vậy thiết diện cần tìm là tam giác MNP. Ta có: \(ME\parallel CI\Rightarrow \frac{MN}{CI}=\frac{AM}{AI}\Leftrightarrow \frac{MN}{\frac{AB\sqrt{3}}{2}}=\frac{x}{\frac{AB}{2}}\Leftrightarrow MN=\frac{\frac{AB\sqrt{3}}{2}x}{\frac{AB}{2}}=x\sqrt{3}.\) \(\begin{array}{l}MP\parallel SI \Rightarrow \frac{{MP}}{{SI}} = \frac{{AM}}{{AI}} = \frac{{AP}}{{AS}} \Leftrightarrow \frac{{MP}}{{\frac{{AB\sqrt 3 }}{2}}} = \frac{x}{{\frac{{AB}}{2}}} \Rightarrow MP = \frac{{\frac{{AB\sqrt 3 }}{2}x}}{{\frac{{AB}}{2}}} = x\sqrt 3 \\PN\parallel SC \Rightarrow \frac{{AP}}{{AS}} = \frac{{PN}}{{SC}} \Rightarrow \frac{{PN}}{{SC}} = \frac{{AM}}{{AI}} \Leftrightarrow \frac{{PN}}{{SC}} = \frac{x}{{\frac{{AB}}{2}}} \Leftrightarrow PN = \frac{{xSC}}{{\frac{{AB}}{2}}} = 2x\,\,\left( {SC = AB} \right)\end{array}\) Tam giác MNP có MN = MP nên tam giác MNP cân tại M Chọn C. Câu hỏi 18 : Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi, O là giao điểm của hai đường chéo AC và BD. Thiết diện của hình chóp khi cắt bởi mặt phẳng \(\left( \alpha \right)\) qua O song song với AB và SC là hình gì?
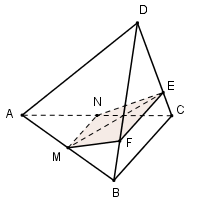
Đáp án: D Phương pháp giải: Sử dụng tính chất: Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) có điểm chung M và lần lượt chứa hai đường thẳng song song d và d’ thì giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) là đường thẳng đi qua M và song song với d và d’ để xác định thiết diện của hình chóp. Chứng minh thiết diện là hình thang mà không là hình bình hành. Lời giải chi tiết: Trong (ABCD) qua O kẻ PQ // AB \(\left( P\in BC,Q\in AD \right)\Rightarrow \left( \alpha \right)\cap \left( ABCD \right)=PQ\) Trong (SAC) qua O kẻ OM // SC \(\left( M\in SA \right)\Rightarrow \left( \alpha \right)\cap \left( SAD \right)=MQ.\) Trong (SAB) qua M kẻ MN // AB \(\left( N\in SB \right)\Rightarrow \left( \alpha \right)\cap \left( SAB \right)=MN\) \(\Rightarrow \left( \alpha \right)\cap \left( SBC \right)=NP\) và NP // AC. Vậy thiết diện tạo bởi mp\(\left( \alpha \right)\) và hình chóp là tứ giác MNPQ. Ta có MN // PQ // AB nên MNPQ là hình thang. Ta có MN // OM. Mà \(OM\cap MQ=M\Rightarrow \) NP và MQ không song song với nhau. Vậy MNPQ là hình thang. Chọn D. Câu hỏi 19 : Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và AC, E là điểm trên cạnh CD sao cho ED = 3EC. Thiết diện tạo bởi mp(MNE) và tứ diện ABCD là:
Đáp án: D Phương pháp giải: - Tìm thiết diện dựa vào các yếu tố song song. - Chứng minh thiết diện là hình thang mà không là hình bình hành. Lời giải chi tiết: MN là đường trung bình của tam giác ABC nên MN // BC Ta có: \(\left\{ \begin{array}{l}\left( {MNE} \right) \cap \left( {BCD} \right) = E\\\left( {MNE} \right) \supset MN\\\left( {BCD} \right) \supset BD\\MN\parallel BD\end{array} \right. \Rightarrow \) Giao tuyến của (MNE) và (BCD) là đường thẳng qua E và song song với MN và BC. Trong (BCD) qua E kẻ EF // BC \(\left( F\in BC \right)\). \(\Rightarrow \left( MNE \right)\cap \left( BCD \right)=EF.\) Vậy thiết diện là MNEF có MN // EF \(\Rightarrow \) MNEF là hình thang. Ta có: \(MN = \frac{1}{2}BC.\) \(\begin{array}{l}{\rm{EF}}\parallel {\rm{BC}} \Rightarrow \frac{{EF}}{{BC}} = \frac{{DE}}{{DC}} = \frac{3}{4} \Rightarrow EF = \frac{3}{4}BC\\ \Rightarrow MN \ne EF.\end{array}\) Do đó MNEF chỉ là hình thang mà không là hình bình hành. Chọn D. Câu hỏi 20 : Cho tứ diện ABCD, M thuộc đoạn AB, thiết diện của hình chóp cắt bởi mặt phẳng \(\left( \alpha \right)\) đi qua M song song với BD và AC là:
Đáp án: A Phương pháp giải: - Sử dụng tính chất: Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) có điểm chung M và lần lượt chứa hai đường thẳng song song d và d’ thì giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) là đường thẳng đi qua M và song song với d và d’ để xác định thiết diện. - Chứng minh thiết diện có các cạnh đối song song. Lời giải chi tiết: \(\left\{ \begin{array}{l}M \in \left( \alpha \right) \cap \left( {ABC} \right)\\\left( \alpha \right)\parallel AC \subset \left( {ABC} \right)\end{array} \right. \Rightarrow \)Giao tuyến của \(\left( \alpha \right)\) và (ABC) là đường thẳng qua M và song song với AC, cắt BC tại N \(\Rightarrow MN\parallel AC.\) \(\left\{ \begin{array}{l}N \in \left( \alpha \right) \cap \left( {BCD} \right)\\\left( \alpha \right)\parallel BD \subset \left( {BCD} \right)\end{array} \right. \Rightarrow \) Giao tuyến của \(\left( \alpha \right)\) và (BCD) là đường thẳng qua N và song song với BD, cắt CD tại P \(\Rightarrow NP\parallel BD.\) \(\left\{ \begin{array}{l}P \in \left( \alpha \right) \cap \left( {ACD} \right)\\\left( \alpha \right)\parallel AC \subset \left( {ACD} \right)\end{array} \right. \Rightarrow \) Giao tuyến của \(\left( \alpha \right)\) và (ACD) là đường thẳng qua P và song song với AC, cắt AD tại Q \(\Rightarrow PQ\parallel AC.\) \(\left\{ \begin{array}{l}\left( \alpha \right) \cap \left( {ABD} \right) = MQ\\\left( \alpha \right)\parallel BD \subset \left( {ABD} \right)\end{array} \right. \Rightarrow MQ\parallel BD.\) Vậy thiết diện là MNPQ là hình bình hành. Chọn A. Câu hỏi 21 : Trong không gian, xét vị trí tương đối của đường thẳng với mặt phẳng thì số khả năng xãy ra tối đa là:
Đáp án: B Phương pháp giải: Dựa vào vị trí tương đối của đường thẳng và mặt phẳng trong không gian. Lời giải chi tiết: Trong không gian có 3 vị trí tương đối giữa đường thẳng và mặt phẳng: Đường thẳng cắt mặt phẳng Đường thẳng nằm trong mặt phẳng. Đường thẳng song song với mặt phẳng. Chọn B. Câu hỏi 22 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành thì giao tuyến của (SAD) và (SBC) là:
Đáp án: A Phương pháp giải: Sử dụng tính chất: Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) có điểm chung M và lần lượt chứa hai đường thẳng song song d và d’ thì giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) là đường thẳng đi qua M và song song với d và d’. Lời giải chi tiết: \(\left\{ \begin{array}{l}S \in \left( {SAD} \right) \cap \left( {SBC} \right)\\AD \subset \left( {SAD} \right)\\BC \subset \left( {SBC} \right)\\AD//BC\end{array} \right. \Rightarrow \) Giao tuyến của (SAD) và (SBC) là đường thẳng qua S và song song với AD, BC. Chọn A.
Câu hỏi 23 : Cho hình chóp SABCD có đáy ABCD là hình bình hành tâm O, gọi I là trung điểm của cạnh SC. Mệnh đề nào sau đây sai?
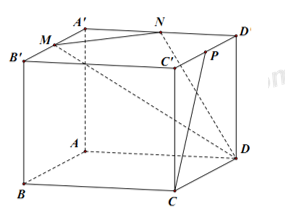
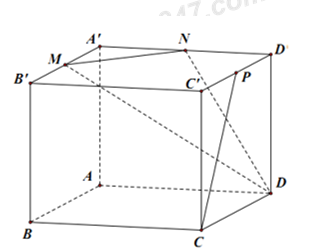
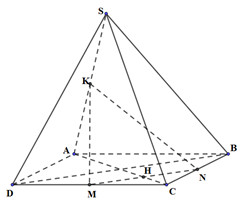
Đáp án: C Phương pháp giải: +) Sử dụng phương án loại trừ để giải bài toán. +) Ta có: \(a\subset \left( \alpha \right);\,\,b//a\Rightarrow b//\left( \alpha \right).\) Lời giải chi tiết: Ta có: O là trung điểm của AC, I là trung điểm của SC \(\Rightarrow OI//SA\) (OI là đường trung bình của tam giác SAC). \(\Rightarrow OI//\left( SAB \right)\Rightarrow \) A đúng. Tương tự \(\Rightarrow OI//\left( SAD \right)\Rightarrow \) B đúng. Ta có: \(\begin{align} & I\in SC\Rightarrow I\in \left( SAC \right);\,\,O\in AC\Rightarrow O\in \left( SAC \right) \\ & O\in BD\Rightarrow O\in \left( IBD \right) \\ \end{align}\) \(\Rightarrow \left( IBD \right)\cap \left( SAC \right)=IO\Rightarrow \) D đúng. Chọn C. Câu hỏi 24 : Cho hình hộp \(ABCD.A'B'C'D'\) có \(M,N,P\) lần lượt là trung điểm của các cạnh \(A'B',\,\,A'D',\,\,C'D'\). Góc giữa đường thẳng \(CP\) và mặt phẳng \((DMN)\) bằng
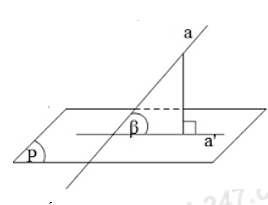
Đáp án: D Phương pháp giải: +) Xác định góc giữa đường thẳng và mặt phẳng: Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P). Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’. +) Nếu \(a//(P)\Rightarrow \left( \widehat{a;(P)} \right)={{0}^{0}}\). Lời giải chi tiết: Ta có: \(MN\) là đường trung bình của tam giác A’B’D’ \(\Rightarrow MN//B'D'\) Mà \(B'D'//BD\Rightarrow MN//BD\Rightarrow M,N,B,D\) đổng phẳng. Lại có \(CP//MB\Rightarrow CP//(MNDB)\) hay \(CP//(MND)\) \(\Rightarrow \left( \widehat{CP;(MND)} \right)={{0}^{0}}\) Chọn: D Câu hỏi 25 : Cho các đường thẳng a, b, c và các mặt phẳng \(\left( \alpha \right),\,\left( \beta \right)\). Giả thiết nào sau đây đủ để kết luân đường thẳng a song song với đường thẳng b?
Đáp án: D Phương pháp giải: Lời giải chi tiết: \(\left\{ \begin{array}{l}a//\left( \alpha \right)\\b//\left( \beta \right)\\\left( \alpha \right) \cap \left( \beta \right) = b\end{array} \right. \Rightarrow a//b\). Chọn: D Câu hỏi 26 : Cho mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(a \not\subset \left( \alpha \right)\). Khẳng định nào sau đây sai?
Đáp án: C Phương pháp giải: Lời giải chi tiết: Khẳng định sai là: Nếu \(a//\left( \alpha \right)\) và \(b \subset \left( \alpha \right)\) thì a // b. Chọn: C Câu hỏi 27 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm tam giác SAB và I là trung điểm của AB. Lấy điểm M trên đoạn AD sao cho \(AD = 3AM\). Đường thẳng qua M và song song với AB cắt CI tại J. Đường thẳng JG không song song với mặt phẳng:
Đáp án: B Phương pháp giải: Sử dụng định lí Ta-let. Lời giải chi tiết:
Ta có: \(\frac{{IJ}}{{IC}} = \frac{{AM}}{{AD}} = \frac{1}{3} = \frac{{IG}}{{IS}} \Rightarrow JG//SC \Rightarrow \left\{ \begin{array}{l}JG//\left( {SCD} \right)\\JG//\left( {SAC} \right)\\JG//\left( {SBC} \right)\end{array} \right.\). Chọn: B Câu hỏi 28 : Cho hai đường thẳng phân biệt a, b và mặt phẳng \(\left( \alpha \right)\). Mệnh đề nào sau đây là sai?
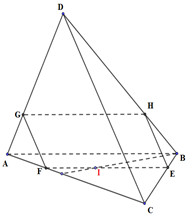
Đáp án: C Phương pháp giải: Lời giải chi tiết: *) \(\left\{ \begin{array}{l}a \not\subset \left( \alpha \right)\\a//b\\b \subset \left( \alpha \right)\end{array} \right. \Rightarrow a//\left( \alpha \right)\): đúng vì theo định nghĩa *) \(\left\{ \begin{array}{l}a \cap \left( \alpha \right) = K\\b \cap \left( \alpha \right) = K\end{array} \right. \Rightarrow a \cap b = K\): đúng vì a, b phân biệt *) \(\left\{ \begin{array}{l}a//b\\b//\left( \alpha \right)\end{array} \right. \Rightarrow a//\left( \alpha \right)\): sai trong trường hợp \(a \subset \left( \alpha \right)\) *) \(\left\{ \begin{array}{l}a//b\\a \cap \left( \alpha \right) = M\end{array} \right. \Rightarrow b \cap \left( \alpha \right) = N\): đúng. Chọn: C Câu hỏi 29 : Cho tứ diện ABCD, điểm I nằm trong tam giác ABC, mặt phẳng \(\left( \alpha \right)\) đi qua I và song song với AB và CD. Thiết diện của tứ diện ABCD và mặt phẳng \(\left( \alpha \right)\)là:
Đáp án: C Phương pháp giải: Xác định giao điểm của \(\left( \alpha \right)\) với các cạnh của tứ diện ABCD (nếu có). Từ đó kết luận thiết diện. Lời giải chi tiết:
Qua I dựng đường thẳng song song AB, cắt AC, BC lần lượt tại F, E Qua F, E lần lượt dựng các đường thẳng song song DC, cắt AD, BD tại G, H \( \Rightarrow \left( {EFGH} \right) \equiv \left( \alpha \right)\) Thiết diện của tứ diện ABCD và mặt phẳng \(\left( \alpha \right)\)là: hình bình hành EFGH (do \(GF//HE\) và \(GF = HE\)) Chọn: C Câu hỏi 30 : Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Giao tuyến của 2 mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBC} \right)\) là đường thẳng song song với đường thẳng nào sau đây?
Đáp án: C Phương pháp giải: Hai mặt phẳng chứa 2 đường thẳng song song cắt nhau theo giao tuyến song song với 2 mặt phẳng đó. Lời giải chi tiết: Vì AD // BC, (SAD) và (SBC) có điểm S chung nên giao tuyến của 2 mặt phẳng (SAD) và (SBC) đi qua S và song song với AD, BC. Chọn C. Câu hỏi 31 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M, N, K lần lượt là trung điểm của các cạnh DC, BC, SA. Gọi H là giao điểm của AC và MN. Trong các khẳng định sau, khẳng định nào sai?
Đáp án: C Phương pháp giải: Lời giải chi tiết:
MN là đường trung bình của tam giác BCD \( \Rightarrow MN//BD \Rightarrow MN//\left( {SBD} \right)\) \(MN \cap AC = H,\,\,AC \subset \left( {SAC} \right)\,\, \Rightarrow MN \cap \left( {SAC} \right) = H\) MN // (ABCD) là khẳng định sai: do \(MN \subset \left( {ABCD} \right)\) Chọn: C Câu hỏi 32 : Đường thẳng a và mặt phẳng (P) song song với nhau nếu:
Đáp án: D Phương pháp giải: Một đường thẳng (d) song song với mặt phẳng (P) nếu (d) song song với một đường thẳng trong (P). Lời giải chi tiết: Chọn D. Câu hỏi 33 : Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và AC. Đường thẳng MN song song với mặt phẳng:
Đáp án: B Phương pháp giải: Một đường thẳng (d) song song với mặt phẳng (P) nếu (d) song song với một đường thẳng trong (P). Lời giải chi tiết: Xét tam giác ABC có MN là đường trung bình \( \Rightarrow MN//BC\). Mà \(BC \subset \left( {BCD} \right) \Rightarrow MN//\left( {BCD} \right)\). MN không song song với (ABC) do \(M \in AB \Rightarrow M \in \left( {ABC} \right);\,\,N \in AC \Rightarrow N \in \left( {ABC} \right) \Rightarrow MN \subset \left( {ABC} \right)\) Chọn B. Câu hỏi 34 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SB. Mệnh đề nào sau đây là mệnh đề đúng?
Đáp án: D Phương pháp giải: Đường thẳng song song với một mặt phẳng khi và chỉ khi nó song song với một đường thẳng trong mặt phẳng đó. Lời giải chi tiết: Ta có MN là đường trung bình của tam giác SAB \( \Rightarrow MN//AB//CD\). Mà \(CD \subset \left( {SCD} \right) \Rightarrow MN//\left( {SCD} \right)\). \(M \in SA \Rightarrow M \in \left( {SAC} \right);\,\,N \in SB \Rightarrow N \in \left( {SAB} \right) \Rightarrow MN \subset \left( {SAB} \right)\). Chọn D. Câu hỏi 35 : Cho hai đường thẳng a, b và mặt phẳng (P). Chọn mệnh đề đúng trong các mệnh đề sau:
Đáp án: C Phương pháp giải: Lời giải chi tiết: A sai vì \(b//a \subset \left( P \right)\) suy ra b // (P) hoặc \(b \subset \left( P \right)\). B sai vì a, b có thể cắt nhau hoặc trùng nhau. D sai vì a // b, b // (P) thì a // (P) hoặc \(a \subset \left( P \right)\). Chọn C. Câu hỏi 36 : Cho hình chóp S.ABCD. Gọi M, N lần lượt là trọng tâm tam giác SAB, SAD. Gọi P là trung điểm của BC. Mệnh đề nào sau đây đúng?
Đáp án: B Phương pháp giải: \(\left\{ \begin{array}{l}a//b\\b \subset \left( \alpha \right)\\a \not\subset \left( \alpha \right)\end{array} \right. \Rightarrow a//\left( \alpha \right)\) Lời giải chi tiết:
Gọi I là trung điểm của tam giác IBD. Do M, N lần lượt là trọng tâm tam giác SAB, SAD nên, ta có: \(\dfrac{{IN}}{{ID}} = \dfrac{{IM}}{{IB}} = \dfrac{1}{3} \Rightarrow MN//BD\) Mà \(BD \subset \left( {SBD} \right),\,\,MN \not\subset \left( {SBD} \right)\,\, \Rightarrow MN//\left( {SBD} \right)\). Chọn: B Câu hỏi 37 : Cho tứ diện \(ABCD\), gọi \({G_1},\,{G_2}\) lần lượt là trọng tâm các tam giác \(BCD\) và \(ACD\). Mệnh đề nào sau đây SAI?
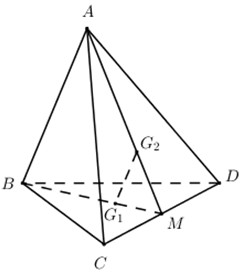
Đáp án: C Phương pháp giải: +) Gọi \(M\) là trung điêm của \(CD\). Chứng minh \(B{G_1},\,\,A{G_2},\,\,CD\) đồng quy tại \(M\). +) Chứng minh \({G_1}{G_2}//AB\). Lời giải chi tiết:
Gọi \(M\) là trung điểm của \(CD\) ta có : \(B,\,\,{G_1},\,\,M\) thẳng hàng, \(A,\,\,{G_2},\,\,M\) thẳng hàng. \( \Rightarrow B{G_1},\,\,A{G_2},\,\,CD\) đồng quy tại \(M\), do đó đáp án \(D\) đúng. Ta có: \(\dfrac{{M{G_1}}}{{MB}} = \dfrac{{M{G_2}}}{{MA}} = \dfrac{1}{3} \Rightarrow {G_1}{G_2}//AB\) (Định lí Ta-lét đảo). Mà \(AB \subset \left( {ABD} \right),\,\,AB \subset \left( {ABC} \right) \Rightarrow {G_1}{G_2}//\left( {ABD} \right),\,\,{G_1}{G_2}//\left( {ABC} \right)\), do đó các đáp án \(A,B\) đúng. Chọn C. Câu hỏi 38 : Cho lăng trụ \(ABC.A'B'C'.\) Gọi \(M,\,N\) lần lượt là trung điểm của \(AA'\) và \(B'C'.\) Khi đó đường thẳng \(AB'\) song song với mặt phẳng:
Đáp án: B Phương pháp giải: Sử dụng quan hệ song song trong không gian để chứng mình và chọn đáp án đúng. Lời giải chi tiết:
+) Đáp án A: Ta có \(\left( {C'MN} \right)\) chính là \(\left( {C'MB'} \right)\) \( \Rightarrow AB' \cap \left( {C'MN} \right) = \left\{ {B'} \right\} \Rightarrow \) loại đáp án A. +) Đáp án C: Ta có \(AB' \cap A'B\) vì hai đường thẳng cùng thuộc \(\left( {A'B'BA} \right) \Rightarrow \) loại đáp án C. +) Đáp án D: Ta có: \(AB' \cap BM\) do hai đường thẳng này cùng thuộc \(\left( {A'B'BA} \right) \Rightarrow \)loại đáp án D Chọn B Câu hỏi 39 : Trong không gian cho hai đường thẳng \(a,b\) và mặt phẳng \(\left( P \right).\) Mệnh đề nào sau đây đúng?
Đáp án: B Phương pháp giải: Sử dụng lý thuyết về quan hệ song song và vuông góc của đường thẳng và mặt phẳng trong không gian Lời giải chi tiết: Đáp án A : Sai vì có thể xảy ra trường hợp \(a,b\) cắt nhau (cùng nằm trong mặt phẳng song song \(\left( P \right)\)) hoặc có thể chéo nhau. Đáp án B : Đúng. Đáp án C : Sai vì có thể xảy ra trường hợp \(a,b\) trùng nhau. Đáp án D : Sai vì có thể xảy ra trường hợp \(b \subset \left( P \right)\). Chọn B. Câu hỏi 40 : Cho hình chóp \(S.ABCD\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(SA\) và \(SC\). Khẳng định nào sau đây là đúng?
Đáp án: A Phương pháp giải: \(\left\{ \begin{array}{l}a\parallel b\\b \subset \left( P \right)\end{array} \right. \Rightarrow a\parallel \left( P \right)\). Lời giải chi tiết:
Vì \(MN\) là đường trung bình của tam giác \(SAC\). \( \Rightarrow MN\parallel AC\) (Tính chất đường trung bình). Mà \(AC \subset \left( {ABCD} \right) \Rightarrow MN\parallel \left( {ABCD} \right)\). Chọn A. Quảng cáo
|














 Gọi \(P\) là trung điểm của \(B'C'.\)
Gọi \(P\) là trung điểm của \(B'C'.\)