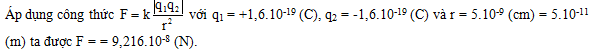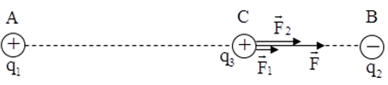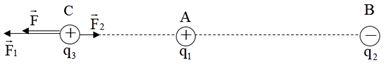Phương pháp giải:

Áp dụng công thức tính lực điện culông \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

Lời giải chi tiết:

Đáp án D

Giải hệ \(\left\{ \begin{array}{l}{2.10^{ - 6}} = {9.10^9}\frac{{\left| {{q_1}{q_2}} \right|}}{{{d^2}}}\\{5.10^{ - 7}} = {9.10^9}\frac{{\left| {{q_1}{q_2}} \right|}}{{{{\left( {d + 10} \right)}^2}}}\end{array} \right. =  > d = 10cm\)

Phương pháp giải:

Sử dụng công thức tính lực Cu- lông trong điện môi

Lời giải chi tiết:

Trong chân không, hằng số điện môi bằng 1. Trong các môi trường khác, hằng số điện môi là ε.

Ta có :  

\(F = k.\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} = > \varepsilon = \frac{{{F_1}}}{{{F_2}}} = \frac{{12}}{4} = 3\)

Phương pháp giải:

Vận dụng biểu thức của định luật Cu-lông: \(F=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{\varepsilon {{r}^{2}}}\) 

Lời giải chi tiết:

Ta có:

+ Khi khoảng cách giữa hai điện tích điểm là r: \(F=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{\varepsilon {{r}^{2}}}\)

+ Khi khoảng cách giữa hai điện tích điểm là 3r: \(F'=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{\varepsilon {{\left( 3r \right)}^{2}}}=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{9\varepsilon {{r}^{2}}}\)

=> \(\frac{F}{F'}=9\to F'=\frac{F}{9}\)

Phương pháp giải:

Lực tương tác giữa hai điện tích điểm trong chân không:       \(F=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}\)

Lời giải chi tiết:

Lực tương tác giữa hai điện tích điểm trong chân không:       \(F=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}={{10}^{-5}}N\)

Lực tương tác lúc sau giữa hai điện tích điểm: \(F'=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{r{{'}^{2}}}={{2,5.10}^{-6}}N\)

Vì F = 4F’ nên r’ = 2r = 2.4 = 8cm

Lời giải chi tiết:

Phương pháp giải:

Công thức tính lực Cu – lông và lực hấp dẫn: \({F_C} = {{k\left| {{q_1}{q_2}} \right|} \over {{r^2}}};{F_{hd}} = {{G{m_1}{m_2}} \over {{r^2}}}\)

Lời giải chi tiết:

Ta có: 

\(\left\{ \matrix{
{F_C} = {{k\left| {{q_1}{q_2}} \right|} \over {{r^2}}} = {{k{e^2}} \over {{r^2}}} \hfill \cr
{F_{hd}} = {{G{m_1}{m_2}} \over {{r^2}}} = {{Gm_e^2} \over {{r^2}}} \hfill \cr} \right. \Rightarrow {{{F_C}} \over {{F_{hd}}}} = {{k{e^2}} \over {Gm_e^2}} = {{{{9.10}^9}.{{\left( {{{1,6.10}^{ - 19}}} \right)}^2}} \over {{{6,67.10}^{ - 11}}.{{\left( {{{9,1.10}^{ - 31}}} \right)}^2}}} = {4,2.10^{42}}\)

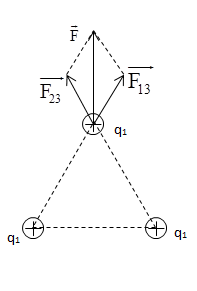
Phương pháp giải:

Lời giải chi tiết:

Đáp án D

+ Ta có \({F_c} = {{{F_0}} \over \varepsilon }\) với F₀ là lực tương tác tĩnh điện trong không khí và F_C là lực tương tác tĩnh điện trong môi trường điện môi ε

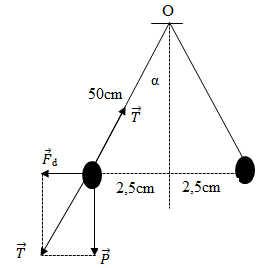
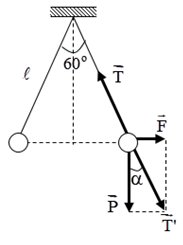
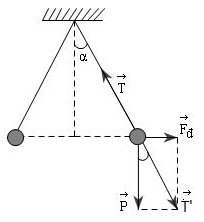
Phương pháp giải:

Sử dụng công thức tính lực Culong, quy tắc tổng hợp lực

Lời giải chi tiết:

Lực do điện tích q₁ và q₂ tác dụng lên q₃ là

\({F_{12}} = {F_{23}} = k{{\left| {{q_1}{q_3}} \right|} \over {{a^2}}} = {9.10^9}.{{\left| {{{4.10}^{ - 10}}{{.3.10}^{ - 12}}} \right|} \over {0,{1^2}}} = 1,{08.10^{ - 9}}N\)

Ta biểu diễn 2 lực

Lực do q₁ và q₂ tác dụng lên q₃ là

 \(F = \sqrt {F_{13}^2 + F_{23}^2 + 2{F_{13}}{F_{23}}\cos {{60}^ \circ }} = {F_{13}}\sqrt 3 = 1,{87.10^{ - 9}}N\)

Chọn D

Phương pháp giải:

Định luật Cu – lông \(F = {{k\left| {{q_1}{q_2}} \right|} \over {{r^2}}}\)

Lời giải chi tiết:

Từ hình vẽ ta có:

 \(\tan \alpha  = {{{F_d}} \over P} = {{2,5} \over {\sqrt {{{50}^2} - {{2,5}^2}} }} \Rightarrow {F_d} = {{2,5} \over {\sqrt {{{50}^2} - {{2,5}^2}} }}P = {{2,5} \over {\sqrt {{{50}^2} - {{2,5}^2}} }}.0,2.10 = 0,1N\)

Lại có: \({F_d} = {{k{q^2}} \over {{r^2}}} \Rightarrow q = \sqrt {{{{F_d}.{r^2}} \over k}}  = \sqrt {{{0,1.{{\left( {{{5.10}^{ - 2}}} \right)}^2}} \over {{{9.10}^9}}}}  = {1,7.10^{ - 7}}C\)

Phương pháp giải:

Áp dụng công thức tính lực điện Cu lông : \(F = k\frac{{\left| q \right|}}{{{r^2}}}\)

Lời giải chi tiết:

Đáp án C

Lực Cu-lông: khi q không đổi \(F = k\frac{{\left| q \right|}}{{{r^2}}} =  > F \sim \frac{1}{{{r^2}}}\). Đồ thị biểu diễn lực tương tác Culông giữa hai điện tích điểm quan hệ với bình phương khoảng cách giữa hai điện tích là đường hypebol. 

Phương pháp giải:

Phương pháp: Áp dụng biểu thức tính lực tương tác tĩnh điện: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Lời giải chi tiết:

Hướng dẫn giải:

Theo định luật Cu-lông, ta có: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

+ Khi 2 điện tích đặt trong không khí, ε = 1: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

+ Khi đặt 2 điện tích vào trong dầu có ε = 2, và \(r' = \frac{r}{3}\) : \(F' = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon r{'^2}}} = k\frac{{\left| {{q_1}{q_2}} \right|}}{{2.\frac{{{r^2}}}{9}}} = \frac{9}{2}k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = \frac{9}{2}F\)

=> Chọn D

Phương pháp giải:

Phương pháp:

+ Điện tích của 1 electron là: e = -1,6.10^-19C

+ Áp dụng biểu thức tính lực tương tác tĩnh điện: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Lời giải chi tiết:

Hướng dẫn giải:

Ta có:

+ Điện tích của 1 electron là: e = -1,6.10^-19C

Mỗi hạt bụi chứa 5.10⁸ electron => Mỗi hạt bụi có điện tích là q₁ = q₂ = q = 5.10⁸.(-1,6.10^-19) = - 8.10^-11 C

+Lực đẩy tĩnh điện giữa hạt: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} = k\frac{{\left| {{q^2}} \right|}}{{\varepsilon {r^2}}} = {9.10^9}\frac{{\left| {{{( - {{8.10}^{ - 11}})}^2}} \right|}}{{1.{{({{2.10}^{ - 2}})}^2}}} = 1,{44.10^{ - 7}}N\)

=> Chọn C

Lời giải chi tiết:

Đáp án C

Sau khi tiếp xúc nhau hai quả cầu sẽ cân bằng điện tích q1=q2=1.10^–9 C  có tích độ lớn hai điện tích bằng 1/8 độ lớn tích độ lớn hai điện tích ban đầu mà khoảng cách là không đổi do đó sau khi tiếp xuacs nhau rồi tách ra  chúng đẩy nhau bằng lực 0,5.10^–5 N  

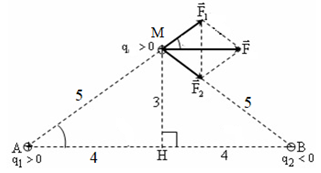
Phương pháp giải:

Lời giải chi tiết:

Đáp án D

\(\left\{ \begin{array}{l}BC + BA = 60cm\\\frac{{{q_1}q}}{{B{A^2}}} = \frac{{{q_1}q}}{{4.B{C^2}}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}BC + CB = 60\\\frac{{BA}}{{BC}} = 2\end{array} \right.\)

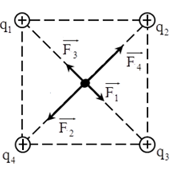
Phương pháp giải:

Tổng hợp lực \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Công thức tính lực tương tác giữa hai điện tích điểm: \(F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

Lời giải chi tiết:

Đáp án A

Gọi H là chân đường cao kẻ từ M xuống AB (H thuộc AB) \( \Rightarrow \left\{ \begin{array}{l}MH = 3cm\\AH = HB = 4cm\\AM = MB = \sqrt {{3^2} + {4^2}}  = 5cm\end{array} \right.\)

F₁ là lực điện do q₁ tác dụng lên q: \({F_1} = k\frac{{\left| {{q_1}q} \right|}}{{A{M^2}}} = 3,{6.10^{ - 4}}N\)

F₂ là lực điện do q₂ tác dụng lên q: \({F_2} = k\frac{{\left| {{q_2}q} \right|}}{{A{M^2}}} = 1,{08.10^{ - 3}}N\)

Lực điện tổng hợp do q₁ và q₂  tác dụng lên q là: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Gọi góc tạo bởi hai véctơ \(\overrightarrow {{F_1},} \overrightarrow {{F_2}} \) là: \(\widehat {{F_1}M{F_2}} = \pi  - \widehat {AMB} = \pi  - 2.\widehat {HMB}\)

Mặt khác: \({\rm{cos}}\widehat {HMB} = \frac{{MH}}{{BM}} = \frac{3}{5} \Rightarrow \widehat {HMB} = 53,{1^0} \Rightarrow 2.\widehat {HMB} = 106,{26^0} \Rightarrow \widehat {{F_1}M{F_2}} = 73,{74^0}\)

Ta có: \({F^2} = F_1^2 + F_2^2 + 2{F_1}{F_2}{\rm{cos}}\alpha  = {(3,{6.10^{ - 4}})^2} + {(1,{08.10^{ - 3}})^2} + 2.3,{6.10^{ - 4}}.1,{08.10^{ - 3}}{\rm{cos73,74}} \Rightarrow F = 1,{23.10^{ - 3}}N\)

Phương pháp giải:

+ Lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

+ Hai điện tích cùng dấu thì đẩy nhau, hai điện tích trái dấu thì hút nhau.

+ Lực tổng hợp tác dụng lên điện tích điểm: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

+ Vẽ hình, sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Biểu diễn các lực tác dụng lên q₀ như hình vẽ:

Lực tổng hợp tác dụng lên q₀: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + \overrightarrow {{F_4}} \)

Ta có: \(\left\{ \begin{array}{l}{q_{1\;}} = {q_{2\;}} = {q_{3\;}} = {q_4}\\OA = OB = OC = OD\end{array} \right. \Rightarrow {F_1} = {F_2} = {F_3} = {F_4}\)

Mặt khác: \(\left\{ \begin{array}{l}\overrightarrow {{F_1}}  \uparrow  \downarrow \overrightarrow {{F_3}}  \Rightarrow {F_{13}} = \left| {{F_1} - {F_3}} \right| = 0\\\overrightarrow {{F_2}}  \uparrow  \downarrow \overrightarrow {{F_4}}  \Rightarrow {F_{24}} = \left| {{F_2} - {F_4}} \right| = 0\end{array} \right. \Rightarrow \overrightarrow F  = \overrightarrow {{F_{13}}}  + \overrightarrow {{F_{24}}}  = 0\)

Chọn D.

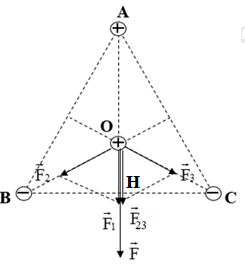
Phương pháp giải:

Phương pháp: Công thức tính lực tương tác: \(F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Lời giải chi tiết:

Cách giải:

Hai điện tích đẩy nhau nên chúng cùng dấu, mặt khác tổng hai điện tích này là số âm do đó có hai điện tích đều âm

Ta có: \(F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}} \Rightarrow \left| {{q_1}{q_2}} \right| = \frac{{F.{r^2}}}{k} = {8.10^{ - 12}} \Rightarrow {q_1}{q_2} = {8.10^{ - 12}}\,\,\,\left( 1 \right)\)

Kết hợp với giả thuyết q₁ + q₂ = - 6.10^-6 C   (2).

Từ (1) và (2) ta có hệ phương trình: \(\begin{array}{l}\left\{ \begin{array}{l}{q_1}.{q_2}\; = {8.10^{ - 12}}\\{q_1} + {q_2}\; =  - {6.10^{ - 6}}\;\;\end{array} \right. \Rightarrow \left( \begin{array}{l}\left\{ \begin{array}{l}{q_1} =  - {2.10^{ - 6}}C\\{q_2} =  - {4.10^{ - 6}}C\end{array} \right.\\\left\{ \begin{array}{l}{q_1} =  - {4.10^{ - 6}}C\\{q_2} =  - {2.10^{ - 6}}C\end{array} \right.\end{array} \right.\\\end{array}\)

Do: \(\left| {{q_1}} \right| > \left| {{q_2}} \right| \Rightarrow \left\{ \begin{array}{l}{q_1} =  - {4.10^{ - 6}}C\\{q_2} =  - {2.10^{ - 6}}C\end{array} \right.\)

Chọn B

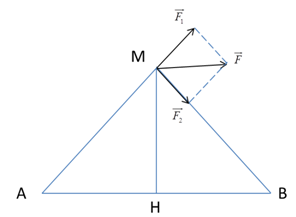
Phương pháp giải:

+ Lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

+ Hai điện tích cùng dấu thì đẩy nhau, hai điện tích trái dấu thì hút nhau.

+ Lực tổng hợp tác dụng lên điện tích điểm: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

+ Vẽ hình, sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Biểu diễn các lực tác dụng lên q₀ như hình vẽ:

Gọi H là chân đường cao kẻ từ A xuống BC. Ta có:

\(OA = \dfrac{2}{3}AH = \dfrac{2}{3}.\sqrt {A{B^2} - B{H^2}}  = \dfrac{2}{3}.\sqrt {{6^2} - {3^2}}  = 2\sqrt 3 cm\)

Ta thấy: \(\left\{ \begin{array}{l}\left| {{q_{1\;}}} \right| = {6.10^{ - 9}}C\\\left| {{q_{2\;}}} \right| = \left| {{q_{3\;}}} \right| = {8.10^{ - 9}}C\\OA = OB = OC = 2\sqrt 3 cm\end{array} \right. \Rightarrow {F_2} = {F_3}\)

Lực tổng hợp tác dụng lên q₀: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

Với: \(\left\{ \begin{array}{l}{F_1} = \dfrac{{k.\left| {{q_0}{q_1}} \right|}}{{O{A^2}}} = \dfrac{{{{9.10}^9}.\left| {{{6.10}^{ - 9}}{{.8.10}^{ - 9}}} \right|}}{{{{\left( {2\sqrt 3 {{.10}^{ - 2}}} \right)}^2}}} = 3,{6.10^{ - 4}}N\\{F_2} = {F_3} = \dfrac{{k.\left| {{q_0}{q_2}} \right|}}{{O{B^2}}} = \dfrac{{{{9.10}^9}.\left| {{{8.10}^{ - 9}}.\left( { - {{8.10}^{ - 9}}} \right)} \right|}}{{{{\left( {2\sqrt 3 {{.10}^{ - 2}}} \right)}^2}}} = 4,{8.10^{ - 4}}N\end{array} \right.\)

Ta có: \(\overrightarrow {{F_{23}}}  = \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

Từ hình vẽ ta thấy hình bình hành tạo bởi \(\overrightarrow {{F_2}} \) và \(\overrightarrow {{F_3}} \) là hình thoi và \(\left( {\overrightarrow {{F_2}} ;\overrightarrow {{F_3}} } \right) = {60^0}\)

\( \Rightarrow {F_{23}} = 2{F_2}.cos60 = {F_2} = \dfrac{{k.\left| {{q_0}{q_2}} \right|}}{{O{B^2}}} = 4,{8.10^{ - 4}}N\)

Ta có: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_{23}}} \)

Mà \(\overrightarrow {{F_1}}  \uparrow  \uparrow \overrightarrow {{F_{23}}}  \Rightarrow F = {F_1} + {F_{23}} = 3,{6.10^{ - 4}} + 4,{8.10^{ - 4}} = 8,{4.10^{ - 4}}N\)

Chọn B.

Phương pháp giải:

Định luật Cu – lông \(F = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

Điều kiện cân bằng: \(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + ... + \overrightarrow {{F_n}}  = 0\)

Phân tích các lực tác dụng vào vật trên hình vẽ và sử dụng các kiến thức hình học.

Lời giải chi tiết:

Khi quả cầu cân bằng thì: \(\overrightarrow P  + \overrightarrow T  + \overrightarrow {{F_d}}  = 0\)

Đặt \(\overrightarrow {T'}  = \overrightarrow P  + \overrightarrow {{F_d}}  \Rightarrow \overrightarrow {T'}  + \overrightarrow T  = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {T'} \, \uparrow  \downarrow \overrightarrow T \\T' = T\end{array} \right.\)

Biểu diễn các lực tác dụng lên quả cầu:

+ Từ hình vẽ ta có:

\(\begin{array}{l}\tan \alpha  = \dfrac{{{F_d}}}{P} \Rightarrow {F_d} = P.\tan \alpha  = mg.\tan \alpha \\ \Rightarrow {F_d} = {5.10^{ - 3}}.10.\tan 30 = 0,029N\end{array}\)

+ Khi hai dây treo hợp với nhau một góc 60⁰thì khoảng cách giữa hai điện tích bằng:

\(l = 10cm = 0,1m\)

+ Mà: \(\left\{ \begin{array}{l}F = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\\\left| {{q_1}} \right| = \left| {{q_1}} \right| = \left| q \right|\end{array} \right. \Rightarrow F = k.\dfrac{{{q^2}}}{{{l^2}}} \Rightarrow \left| q \right| = \sqrt {\dfrac{{F.{l^2}}}{k}} \)

Thay số ta được: \(\left| q \right| = \sqrt {\dfrac{{0,029.0,{1^2}}}{{{{9.10}^9}}}}  = 1,{8.10^{ - 7}}C\)

+ Vậy tổng độ lớn điện tích đã truyền cho hai quả cầu là: \(Q = 2.\left| q \right| = 3,{6.10^{ - 7}}\;C\)

Chọn A.

Phương pháp giải:

Công thức tính lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Hợp lực tác dụng lên điện tích: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Vẽ hình. Sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Điện tích q₃ sẽ chịu hai lực tác dụng của q₁ và q₂ là:\(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} \)

Lực tổng hợp tác dụng lên q₃ là: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Vì C cách đều A, B nên C nằm trên đường trung trực của đoạn AB.

Ta có: \(\left\{ \begin{array}{l}{F_1} = \dfrac{{k\left| {{q_1}{q_3}} \right|}}{{A{C^2}}} = 23,{04.10^{ - 3}}N\\{F_2} = \dfrac{{k\left| {{q_2}{q_3}} \right|}}{{C{B^2}}} = 23,{04.10^{ - 3}}N\end{array} \right.\)

Vì F₁ = F₂  nên \(\overrightarrow F \) nằm trên đường phân giác góc và \(\widehat {\left( {\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} } \right)} \Rightarrow \overrightarrow F  \bot CH\)(phân giác của hai góc kề bù)

\( \Rightarrow \overrightarrow F //AB \Rightarrow \alpha  = \widehat {\left( {\overrightarrow {{F_1}} ,\overrightarrow F } \right)} = \widehat {CAB}\)

Độ lớn lực tổng hợp : \(F = 2.{F_1}.\cos \alpha  = 2.{F_1}.\dfrac{{AH}}{{AC}} = 2.23,{04.10^{ - 3}}.\dfrac{3}{5} = 27,{648.10^{ - 3}}N\)

Chọn B.

Lời giải chi tiết:

Phương pháp giải:

Sử dụng nguyên lý chống chất điện trường

Lời giải chi tiết:

Áp dụng công thức tính cường độ điện trường :  \(E = {{k.|q|} \over {{r^2}}};\overrightarrow E  = \overrightarrow {{E_1}}  + \overrightarrow {{E_2}} \)

Vì tam giác ABC đều nên mỗi góc bằng 60⁰. Nên góc giữa hai vecto là 120⁰.

Ta có:  \({E_1} = {E_2} = {{{{9.10}^9}{{.4.10}^{ - 6}}} \over {{{0,3}^2}}} = {4.10^5}V/m \Rightarrow E = \sqrt {E_1^2 + E_2^2 + 2.{E_{1.}}.{E_2}.\cos {{120}^0}}  = {4.10^5}V/m\)

Phương pháp giải:

Phương pháp: Áp dụng biểu thức tính lực tương tác tĩnh điện: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Lời giải chi tiết:

Hướng dẫn giải:

Ta có, q₁.q₂ < 0 => lực tương tác giữa hai điện tích là lực hút

Theo định luật Cu-lông, ta có: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} = {9.10^9}\frac{{\left| {{{3.10}^{ - 6}}.( - {{3.10}^{ - 6}})} \right|}}{{2.{{(0,03)}^2}}} = 45N\)

=> Chọn A

Phương pháp giải:

Phương pháp: Áp dụng biểu thức tính lực tương tác tĩnh điện: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Lời giải chi tiết:

Hướng dẫn giải:

Theo định luật Cu-lông, ta có: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

- Đặt trong chân không: => ε = 1

\(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} \to r = \sqrt {k\frac{{\left| {{q_1}{q_2}} \right|}}{F}}  = \sqrt {{{9.10}^9}\frac{{\left| {{{10}^{ - 7}}{{.4.10}^{ - 7}}} \right|}}{{0,1}}}  = 0,06m = 6cm\)

=> Chọn D

Phương pháp giải:

Phương pháp: Áp dụng biểu thức tính lực tương tác tĩnh điện: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Lời giải chi tiết:

Hướng dẫn giải:

Ta có, lực tương tác giữa hai điện tích điểm: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} \to \left| {{q_1}{q_2}} \right| = \frac{{F.{r^2}}}{{\varepsilon k}} = \frac{{1,{{8.10}^{ - 4}}.{{(0,05)}^2}}}{{{{1.9.10}^9}}} = {5.10^{ - 17}}\)

Mặt khác, ta có 2 điện tích giống nhau=>\(\;{q_1} = {q_2} =  \pm \sqrt {{{5.10}^{ - 17}}}  =  \pm 7,{07.10^{ - 9}}C\)

=> Chọn D

Phương pháp giải:

Phương pháp:

+ Vận dụng lí thuyết về nhiễm điện do cọ xát

+ Áp dụng định luật bảo toàn điện tích

Lời giải chi tiết:

Hướng dẫn giải:

Ta có:

+ Ban đầu 2 vật cô lập tức điện tích tổng cộng bằng 0 vì cả 2 đều trung hòa điện

+ Sau khi cọ sát, hai vật đều nhiễm điện - nhưng tổng đại số điện tích của 2 vật trong hệ vẫn bằng 0 => 2 vật đều tích điện nhưng trái dấu và có độ lớn bằng nhau nói cách khác độ lớn điện tích dương xuất hiện trên vật này đúng bằng độ lớn điện tích âm xuất hiện trên vật kia.

Theo đầu bài, ta có thanh ebônít sau khi cọ xát với tấm dạ thì có điện tích -3.10^-8C => tấm dạ có điện tích 3.10^-8C

=> Chọn C

Phương pháp giải:

Phương pháp:

+ Áp dụng biểu thức tính lực tương tác tĩnh điện: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

+ Áp dụng biểu thức xác định lực hấp dẫn giữa hai vật: \(F = G\frac{{{m^2}}}{{{r^2}}}\)

Lời giải chi tiết:

Hướng dẫn giải:

Ta có:

- Lực đẩy giữa hai prôtôn: \({F_1} = k\frac{{{q^2}}}{{{r^2}}}\)

- Lực hấp dẫn giữa hai prôtôn:\({F_2} = G\frac{{{m^2}}}{{{r^2}}}\)

- Lập tỉ số: \(\frac{{{F_1}}}{{{F_2}}} = \frac{{k{q^2}}}{{G{m^2}}} = \frac{{{{9.10}^9}{{\left( {1,{{6.10}^{ - 19}}} \right)}^2}}}{{6,{{67.10}^{ - 11}}.{{\left( {1,{{67.10}^{ - 27}}} \right)}^2}}} \approx 1,{24.10^{36}}\)      

\( =  > {F_1} = 1,{24.10^{36}}{F_2}\)     (Lần)

=> Chọn D

Phương pháp giải:

Phương pháp:

+ Áp dụng biểu thức tính lực tương tác tĩnh điện: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

+ Phương pháp tổng hợp lực

+ Vận dụng hệ thức lượng trong tam giác

Lời giải chi tiết:

Hướng dẫn giải:     

Vị trí các điện tích như hình vẽ.

+  Lực do q₁ tác dụng lên q_o:    \({F_{10}} = k\frac{{\left| {{q_1}{q_0}} \right|}}{{A{C^2}}} = {9.10^9}\frac{{\left| {{{10}^{ - 7}}{{.10}^{ - 7}}} \right|}}{{0,{{05}^2}}} = 0,036N\)

+  Lực do q₂ tác dụng lên q_o:  \({F_{20}} = {F_{10}} = 0,036N\)( do \(\left| {{q_1}} \right| = \left| {{q_2}} \right|\))

+  Do \({F_{20}} = {F_{10}}\) nên hợp lực F_o tác dụng lên q_o:

\(\begin{array}{l}{F_o} = 2{F_{10}}.\cos {C_1} = 2.{F_{10}}.\cos A = 2.{F_{10}}.\frac{{AH}}{{AC}}\\{F_o} = 2.0,036.\frac{4}{5} = 57,{6.10^{ - 3}}N\end{array}\)

+ Vậy \({\vec F_o}\) có phương // AB, cùng chiều với vectơ \(\overrightarrow {AB} \) (hình vẽ) và có độ lớn: \({F_o} = 57,{6.10^{ - 3}}N\)

=> Chọn A

Phương pháp giải:

Công thức tính lực tương tác: \(F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Lời giải chi tiết:

Khi đặt trong không khí: \(F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}} \Rightarrow \left| {{q_1}} \right| = \left| {{q_2}} \right| = \sqrt {\frac{{F{r^2}}}{k}}  = \sqrt {\frac{{10.{{\left( {0,12} \right)}^2}}}{{{{9.10}^9}}}}  = {4.10^{ - 6}}C\)

Khi đặt trong dầu: \({F_\varepsilon } = \frac{{k\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} \Rightarrow \varepsilon  = \frac{{k\left| {{q_1}{q_2}} \right|}}{{F{r^2}}} = \frac{{{{9.10}^9}.{{\left( {{{4.10}^{ - 6}}} \right)}^2}}}{{10.{{\left( {0,08} \right)}^2}}} = 2,25\)

Chọn B.

Phương pháp giải:

Hai điện tích cùng dấu thì đẩy nhau, trái dấu thì hút nhau.

Lực tương tác tĩnh điện giữa hai điện tích trong không khí có độ lớn: \(F=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}\)

Lời giải chi tiết:

Vì hai điện tích trái dấu nên chúng hút nhau.

Lực hút tĩnh điện có độ lớn: \(F=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}={{9.10}^{9}}.\frac{{{1,6.10}^{-19}}{{.1,6.10}^{-19}}}{({{0,53.10}^{-10}})}={{8,202.10}^{-8}}N\)

Chọn D

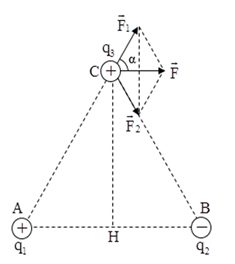
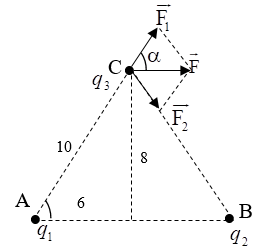
Phương pháp giải:

Công thức tính lực tương tác: \(F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Lời giải chi tiết:

- Hai quả cầu ban đầu hút nhau nên chúng mang điện trái dấu.

- Từ giả thiết bài toán, ta có: \(\left\{ \begin{array}{l}\left| {{q_1}{q_2}} \right| =  - {q_1}{q_2} = \frac{{F{r^2}}}{k} = \frac{{16}}{3}{.10^{ - 12}}\\{\left( {\frac{{{q_1} + {q_2}}}{2}} \right)^2} = \frac{{F{r^2}}}{k} \Rightarrow {q_1} + {q_2} =  \pm \frac{{\sqrt {192} }}{3}{.10^{ - 6}}\end{array} \right.\)

Theo hệ thức Vi – et thì q₁ và q₂ là nghiệm của phương trình:

\({q^2} \pm \frac{{\sqrt {192} }}{3}{.10^{ - 6}}q - \frac{{16}}{3}{.10^{ - 12}} = 0 \Rightarrow \left( \begin{array}{l}\left\{ \begin{array}{l}{q_1} = 0,{96.10^{ - 6}}C\\{q_2} =  - 5,{58.10^{ - 6}}C\end{array} \right.\\\left\{ \begin{array}{l}{q_1} =  - 5,{58.10^{ - 6}}C\\{q_2} = 0,{96.10^{ - 6}}C\end{array} \right.\end{array} \right.\)

Chọn D

Phương pháp giải:

Công thức tính điện tích: q = n.e

Lời giải chi tiết:

Số electron thừa ở quả cầu A là: \({n_A} = \left| {\frac{{{q_A}}}{e}} \right| = {2.10^{12}}\,\,\left( {electron} \right)\)

Số electron thiếu ở quả cầu B là: \({n_B} = \left| {\frac{{{q_B}}}{e}} \right| = 1,{5.10^{12}}\,\,\left( {electron} \right)\)

Chọn C

Phương pháp giải:

Công thức tính lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Hợp lực tác dụng lên điện tích: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Vẽ hình. Sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Biểu diễn các lực của \({q_1};{q_2}\)tác dụng lên \({q_3}\) như hình vẽ:

Ta có: \({F_1} = {F_2} = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = \dfrac{{{{9.10}^9}{{.2.10}^{ - 6}}{{.2.10}^{ - 6}}}}{{0,{{03}^2} + 0,{{04}^2}}} = 14,4N\)

\( \Rightarrow {F_1} = {F_2} \Rightarrow \) hình bình hành là hình thoi

\( \Rightarrow \overrightarrow F \) nằm trên phân giác của \(\left( {\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} } \right)\)

\( \Rightarrow \overrightarrow F  \bot MH\) (phân giác của hai góc kề bù) \( \Rightarrow \overrightarrow F \,//\,AB\)

\( \Rightarrow \left( {\overrightarrow {{F_1}} ;\overrightarrow F } \right) = \widehat {MAB}\)

\(\begin{array}{l} \Rightarrow F = 2.{F_1}.cos\left( {\overrightarrow {{F_1}} ;\overrightarrow F } \right) = 2.{F_1}.cos\widehat {MAB} = 2.{F_1}.\dfrac{{AH}}{{AM}}\\ \Rightarrow F = 2.14,4.\dfrac{4}{5} = 23,04N\end{array}\)

Chọn C.

Phương pháp giải:

Công thức tính lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Hợp lực tác dụng lên điện tích: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Vẽ hình. Sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Điện tích q₃ sẽ chịu hai lực tác dụng của q₁ và q₂ là:\(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} \)

Lực tổng hợp tác dụng lên q₃ là: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

+ Nhận thấy AB² = AC² + CB² → Tam giác ACB vuông tại C

+ Biểu diễn các lực tác dụng lên q₀ như hình vẽ:

Từ hình vẽ ta thấy: \(\overrightarrow {{F_1}} \, \bot \,\overrightarrow {{F_2}}  \Rightarrow F = \sqrt {F_1^2 + F_2^2} \)

Với: \(\left\{ \begin{array}{l}{F_1} = \dfrac{{k.\left| {{q_1}{q_0}} \right|}}{{A{C^2}}} = \dfrac{{{{9.10}^9}.\left| {{{3.10}^{ - 8}}.\left( { - {{2.10}^{ - 8}}} \right)} \right|}}{{0,{{04}^2}}} = 3,{375.10^{ - 3}}N\\{F_2} = \dfrac{{k.\left| {{q_2}{q_0}} \right|}}{{B{C^2}}} = \dfrac{{{{9.10}^9}.\left| {{{2.10}^{ - 8}}.\left( { - {{2.10}^{ - 8}}} \right)} \right|}}{{0,{{03}^2}}} = {4.10^{ - 3}}N\end{array} \right.\)

\( \Rightarrow F = \sqrt {F_1^2 + F_2^2}  = \sqrt {{{\left( {3,{{375.10}^{ - 3}}} \right)}^2} + {{\left( {{{4.10}^{ - 3}}} \right)}^2}}  = 5,{234.10^{ - 3}}N\)

Chọn A.

Phương pháp giải:

Để \({q_0}\) cân bằng thì: \(\overrightarrow {{F_{10}}}  + \overrightarrow {{F_{20}}}  = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{F_{10}}} \, \uparrow  \downarrow \,\overrightarrow {{F_{20}}} \,\,\,\left( 1 \right)\\{F_{10}} = {F_{20}}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Giải (1) \( \Rightarrow \) ba điện tích thẳng hàng

+ Nếu \({q_1};{q_2}\) cùng dấu \( \Rightarrow \) q₀ nằm trong q₁ và q₂.

(Không phụ thuộc vào dấu của q₀)

+ Nếu \({q_1};{q_2}\) trái dấu \( \Rightarrow \) q₀ nằm ngoài q₁ và q₂ và gần điện tích có độ lớn nhỏ hơn.

(Không phụ thuộc vào dấu của q₀)

Lời giải chi tiết:

Để q₃ cân bằng \( \Rightarrow \overrightarrow {{F_{13}}}  + \overrightarrow {{F_{23}}}  = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{F_{13}}} \, \uparrow  \downarrow \,\overrightarrow {{F_{23}}} \,\,\,\left( 1 \right)\\{F_{13}} = {F_{23}}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Do \({q_1};{q_2}\) cùng dấu → Để lực tổng hợp tại C bằng 0 thì C nằm trên đường nối q₁, q₂ và nằm trong khoảng q₁, q₂ \( \Rightarrow AC + BC = AB = 9cm\,\,\,\left( * \right)\)

Lại có: \({F_{13}} = {F_{23}} \Leftrightarrow \dfrac{{k\left| {{q_1}{q_3}} \right|}}{{A{C^2}}}\, = \,\dfrac{{k\left| {{q_2}{q_3}} \right|}}{{B{C^2}}}\)

\( \Leftrightarrow \dfrac{{\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}}\, = \dfrac{{A{C^2}}}{{B{C^2}}} = \dfrac{1}{4} \Rightarrow BC = 2.AC\,\,\,\left( {**} \right)\)

Từ (*) và (**) ta có: \(\left\{ \begin{array}{l}AC + BC = 9\,\\BC = 2.AC\end{array} \right. \Rightarrow \left\{ \begin{array}{l}AC = 3cm\\BC = 6cm\end{array} \right.\)

Vậy \({q_3}\) đặt giữa hai điện tích cách q₁ khoảng 3cm và cách q₂ khoảng 6cm

Chọn B.

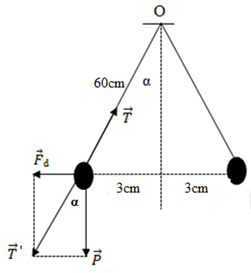
Phương pháp giải:

Công thức tính lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Hợp lực tác dụng lên điện tích: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Vẽ hình. Sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Điện tích q₃ sẽ chịu hai lực tác dụng của q₁ và q₂ là:\(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} \)

Lực tổng hợp tác dụng lên q₃ là: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Ta có: CA = 4cm, CB = 2cm

Vì AC + CB = AB nên C nằm trong đoạn AB.

Biểu diễn các lực tác dụng lên q₃ như hình vẽ:

Từ hình vẽ ta thấy: \(\overrightarrow {{F_1}} \, \uparrow  \uparrow \,\overrightarrow {{F_2}}  \Rightarrow F = {F_1} + {F_2}\)

Với: \(\left\{ \begin{array}{l}{F_1} = \dfrac{{k.\left| {{q_1}{q_3}} \right|}}{{A{C^2}}} = \dfrac{{{{9.10}^9}.\left| {{{8.10}^{ - 8}}{{.8.10}^{ - 8}}} \right|}}{{0,{{04}^2}}} = 0,036N\\{F_2} = \dfrac{{k.\left| {{q_2}{q_3}} \right|}}{{B{C^2}}} = \dfrac{{{{9.10}^9}.\left| { - {{8.10}^{ - 8}}{{.8.10}^{ - 8}}} \right|}}{{0,{{02}^2}}} = 0,144N\end{array} \right.\)

\( \Rightarrow F = {F_1} + {F_2} = 0,036 + 0,144 = 0,18N\)

Chọn B.

Phương pháp giải:

Điều kiện cân bằng: \(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + ... + \overrightarrow {{F_n}}  = 0\)

Phân tích các lực tác dụng vào vật trên hình vẽ và sử dụng các kiến thức hình học.

Lời giải chi tiết:

Phân tích các lực tác dụng lên quả cầu:

Khi quả cầu cân bằng thì: \(\overrightarrow P  + \overrightarrow T  + \overrightarrow {{F_d}}  = 0\)

Đặt \(\overrightarrow {T'}  = \overrightarrow P  + \overrightarrow {{F_d}}  \Rightarrow \overrightarrow {T'}  + \overrightarrow T  = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {T'} \, \uparrow  \downarrow \overrightarrow T \\T' = T\end{array} \right.\)

Hai dây treo hợp với nhau một góc 40⁰\( \Rightarrow \alpha  = {20^0}\)

Từ hình vẽ ta có:

\(\begin{array}{l}\tan \alpha  = \dfrac{{{F_d}}}{P} \Rightarrow {F_d} = P.\tan \alpha  = mg.\tan \alpha \\ \Rightarrow {F_d} = 0,{2.10^{ - 3}}.10.\tan 20 = 7,{23.10^{ - 4}}N\end{array}\)

Ta có: \(T = T'\)

Từ hình vẽ ta có: \(T' = \dfrac{P}{{\cos \alpha }} = \dfrac{{0,{{2.10}^{ - 3}}.10}}{{\cos 20}} = 2,{13.10^{ - 3}}N\)

Vậy lực căng dây: \(T = 2,{13.10^{ - 3}}N\)

Chọn D.

Phương pháp giải:

a) Sử dụng biểu thức định luật Cu-lông: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

b) Vận dụng điều kiện cân bằng của điện tích: \(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + ... = \overrightarrow 0 \)

Lời giải chi tiết:

a)

Lực tương tác giữa hai điện tích: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = {9.10^9}\dfrac{{\left| {{{4.10}^{ - 9}}{{.16.10}^{ - 9}}} \right|}}{{0,{{01}^2}}} = 5,{76.10^{ - 3}}N\)

b)

\({q_1}\) đặt tại A, \({q_2}\) đặt tại B, \({q_0}\) tại C

- Gọi lực do \({q_1}\) tác dụng lên \({q_3}\) là \({F_{13}}\);   lực do \({q_2}\) tác dụng lên \({q_3}\) là \({F_{23}}\)

- Để \({q_3}\) nằm cân bằng: \(\overrightarrow {{F_{13}}}  =  - \overrightarrow {{F_{23}}} \)

- Do \({q_1},{q_2}\) cùng dấu \( \Rightarrow {q_0}\) nằm trong khoảng \(AB\)

Lại có : \({F_{10}} = {F_{20}} \Leftrightarrow k\dfrac{{\left| {{q_1}{q_0}} \right|}}{{A{C^2}}} = k\dfrac{{\left| {{q_2}{q_0}} \right|}}{{B{C^2}}}\)

\( \Rightarrow \dfrac{{A{C^2}}}{{B{C^2}}} = \left| {\dfrac{{{q_1}}}{{{q_2}}}} \right| = \dfrac{1}{4}\)

\( \Rightarrow BC = 2AC\)    (1)

Lại có : \(AC + BC = 1cm\) (2)

Từ (1) và (2) ta suy ra : \(\left\{ \begin{array}{l}AC = \dfrac{1}{3}cm\\BC = \dfrac{2}{3}cm\end{array} \right.\)

- Gọi \(\overrightarrow {{F_{01}}} ,\overrightarrow {{F_{21}}} \) lần lượt là lực do \({q_0},{q_2}\) tác dụng lên \({q_1}\)

+ Điều kiện cân bằng của \({q_1}\): \(\overrightarrow {{F_{01}}}  + \overrightarrow {{F_{21}}}  = \overrightarrow 0 \)

\( \Rightarrow \overrightarrow {{F_{01}}}  =  - \overrightarrow {{F_{21}}} \) (3)

\( \Rightarrow \overrightarrow {{F_{01}}} \) ngược chiều \(\overrightarrow {{F_{21}}} \)

Ta suy ra, \({F_{01}}\) là lực hút

\( \Rightarrow {q_0} < 0\)

+ Lại có: \({F_{01}} = {F_{21}}\)

\(\begin{array}{l} \Leftrightarrow k\dfrac{{\left| {{q_0}{q_1}} \right|}}{{A{C^2}}} = k\dfrac{{\left| {{q_2}{q_1}} \right|}}{{A{B^2}}}\\ \Rightarrow \left| {{q_0}} \right| = \left| {{q_2}} \right|\dfrac{{A{C^2}}}{{A{B^2}}} = {16.10^{ - 9}}\dfrac{{{{\left( {\dfrac{1}{3}} \right)}^2}}}{{{1^2}}} = \dfrac{{16}}{9}{.10^{ - 9}}C\end{array}\)

\( \Rightarrow {q_3} =  - \dfrac{{16}}{9}{.10^{ - 9}}C\)  (do lập luận suy ra \({q_0} < 0\) ở trên) (3)

- Gọi \(\overrightarrow {{F_{02}}} ,\overrightarrow {{F_{12}}} \) lần lượt là lực do \({q_0},{q_1}\) tác dụng lên \({q_2}\)

+ Điều kiện cân bằng của \({q_1}\): \(\overrightarrow {{F_{02}}}  + \overrightarrow {{F_{12}}}  = \overrightarrow 0 \)

\( \Rightarrow \overrightarrow {{F_{02}}}  =  - \overrightarrow {{F_{12}}} \)

\( \Rightarrow \overrightarrow {{F_{02}}} \) ngược chiều \(\overrightarrow {{F_{12}}} \)

\( \Rightarrow {F_{02}}\) là lực hút

\( \Rightarrow {q_0} < 0\)

Lại có: \({F_{02}} = {F_{12}}\)

\(\begin{array}{l} \Leftrightarrow k\dfrac{{\left| {{q_0}{q_2}} \right|}}{{C{B^2}}} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{A{B^2}}}\\ \Rightarrow \left| {{q_0}} \right| = \left| {{q_1}} \right|\dfrac{{C{B^2}}}{{A{B^2}}} = {4.10^{ - 9}}\dfrac{{{{\left( {\dfrac{2}{3}} \right)}^2}}}{{{1^2}}} = \dfrac{{16}}{9}{.10^{ - 9}}C\end{array}\)

\( \Rightarrow {q_3} =  - \dfrac{{16}}{9}{.10^{ - 9}}C\)  (do lập luận suy ra \({q_0} < 0\) ở trên) (4)

Vậy với \({q_3} =  - \dfrac{{16}}{9}{.10^{ - 9}}C\) thì hệ 3 điện tích cân bằng.

Phương pháp giải:

Định luật Cu – lông \(F = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

Điều kiện cân bằng: \(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + ... + \overrightarrow {{F_n}}  = 0\)

Phân tích các lực tác dụng vào vật trên hình vẽ và sử dụng các kiến thức hình học.

Lời giải chi tiết:

Khi quả cầu cân bằng thì: \(\overrightarrow P  + \overrightarrow T  + \overrightarrow {{F_d}}  = 0\)

Đặt \(\overrightarrow {T'}  = \overrightarrow P  + \overrightarrow {{F_d}}  \Rightarrow \overrightarrow {T'}  + \overrightarrow T  = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {T'} \, \uparrow  \downarrow \overrightarrow T \\T' = T\end{array} \right.\)

Biểu diễn các lực tác dụng lên quả cầu:

Từ hình vẽ ta có:

\(\tan \alpha  = \dfrac{{{F_d}}}{P} = \dfrac{3}{{\sqrt {{{60}^2} - {3^2}} }} \Rightarrow {F_d} = \dfrac{3}{{\sqrt {{{60}^2} - {3^2}} }}.P\)

\( \Rightarrow {F_d} = \dfrac{3}{{\sqrt {{{60}^2} - {3^2}} }}.0,5.10 = 0,25N\)

Lại có: \({F_d} = \dfrac{{k{q^2}}}{{{r^2}}} \Rightarrow \left| q \right| = \sqrt {\dfrac{{{F_d}.{r^2}}}{k}}  = \sqrt {\dfrac{{0,25.{{\left( {{{6.10}^{ - 2}}} \right)}^2}}}{{{{9.10}^9}}}}  = 3,{2.10^{ - 7}}C\)

Chọn D.

Phương pháp giải:

Công thức tính lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Hợp lực tác dụng lên điện tích: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Vẽ hình. Sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Điện tích q₃ sẽ chịu hai lực tác dụng của q₁ và q₂ là:\(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} \)

Lực tổng hợp tác dụng lên q₃ là: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Ta có: CA = 4cm, CB = 10cm

Vì CB – CA = AB nên C nằm trên đường AB, ngoài khoảng AB, về phía A.

Biểu diễn các lực tác dụng lên q₃ ta có:

Từ hình vẽ ta thấy: \(\overrightarrow {{F_1}} \, \uparrow  \downarrow \,\overrightarrow {{F_2}}  \Rightarrow F = \left| {{F_1} - {F_2}} \right|\)

Với: \(\left\{ \begin{array}{l}{F_1} = \dfrac{{k.\left| {{q_1}{q_3}} \right|}}{{A{C^2}}} = \dfrac{{{{9.10}^9}.\left| {{{8.10}^{ - 8}}{{.8.10}^{ - 8}}} \right|}}{{0,{{04}^2}}} = {36.10^{ - 3}}N\\{F_2} = \dfrac{{k.\left| {{q_2}{q_3}} \right|}}{{B{C^2}}} = \dfrac{{{{9.10}^9}.\left| { - {{8.10}^{ - 8}}{{.8.10}^{ - 8}}} \right|}}{{0,{1^2}}} = 5,{76.10^{ - 3}}N\end{array} \right.\)

\( \Rightarrow F = \left| {{F_1} - {F_2}} \right| = \left| {{{36.10}^{ - 3}} - 5,{{76.10}^{ - 3}}} \right| = 30,{24.10^{ - 3}}N\)

Chọn D.