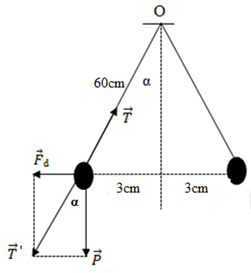
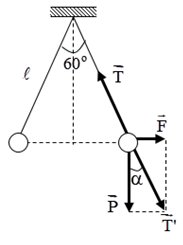
Phương pháp giải:

Định luật Cu – lông \(F = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

Điều kiện cân bằng: \(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + ... + \overrightarrow {{F_n}}  = 0\)

Phân tích các lực tác dụng vào vật trên hình vẽ và sử dụng các kiến thức hình học.

Lời giải chi tiết:

Khi quả cầu cân bằng thì: \(\overrightarrow P  + \overrightarrow T  + \overrightarrow {{F_d}}  = 0\)

Đặt \(\overrightarrow {T'}  = \overrightarrow P  + \overrightarrow {{F_d}}  \Rightarrow \overrightarrow {T'}  + \overrightarrow T  = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {T'} \, \uparrow  \downarrow \overrightarrow T \\T' = T\end{array} \right.\)

Biểu diễn các lực tác dụng lên quả cầu:

Từ hình vẽ ta có:

\(\tan \alpha  = \dfrac{{{F_d}}}{P} = \dfrac{3}{{\sqrt {{{60}^2} - {3^2}} }} \Rightarrow {F_d} = \dfrac{3}{{\sqrt {{{60}^2} - {3^2}} }}.P\)

\( \Rightarrow {F_d} = \dfrac{3}{{\sqrt {{{60}^2} - {3^2}} }}.0,5.10 = 0,25N\)

Lại có: \({F_d} = \dfrac{{k{q^2}}}{{{r^2}}} \Rightarrow \left| q \right| = \sqrt {\dfrac{{{F_d}.{r^2}}}{k}}  = \sqrt {\dfrac{{0,25.{{\left( {{{6.10}^{ - 2}}} \right)}^2}}}{{{{9.10}^9}}}}  = 3,{2.10^{ - 7}}C\)

Chọn D.

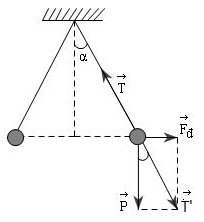
Phương pháp giải:

Điều kiện cân bằng: \(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + ... + \overrightarrow {{F_n}}  = 0\)

Phân tích các lực tác dụng vào vật trên hình vẽ và sử dụng các kiến thức hình học.

Lời giải chi tiết:

Phân tích các lực tác dụng lên quả cầu:

Khi quả cầu cân bằng thì: \(\overrightarrow P  + \overrightarrow T  + \overrightarrow {{F_d}}  = 0\)

Đặt \(\overrightarrow {T'}  = \overrightarrow P  + \overrightarrow {{F_d}}  \Rightarrow \overrightarrow {T'}  + \overrightarrow T  = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {T'} \, \uparrow  \downarrow \overrightarrow T \\T' = T\end{array} \right.\)

Hai dây treo hợp với nhau một góc 40⁰\( \Rightarrow \alpha  = {20^0}\)

Từ hình vẽ ta có:

\(\begin{array}{l}\tan \alpha  = \dfrac{{{F_d}}}{P} \Rightarrow {F_d} = P.\tan \alpha  = mg.\tan \alpha \\ \Rightarrow {F_d} = 0,{2.10^{ - 3}}.10.\tan 20 = 7,{23.10^{ - 4}}N\end{array}\)

Ta có: \(T = T'\)

Từ hình vẽ ta có: \(T' = \dfrac{P}{{\cos \alpha }} = \dfrac{{0,{{2.10}^{ - 3}}.10}}{{\cos 20}} = 2,{13.10^{ - 3}}N\)

Vậy lực căng dây: \(T = 2,{13.10^{ - 3}}N\)

Chọn D.

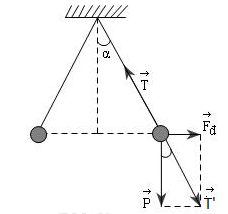
Phương pháp giải:

Điều kiện cân bằng: \(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + ... + \overrightarrow {{F_n}}  = 0\)

Phân tích các lực tác dụng vào vật trên hình vẽ và sử dụng các kiến thức hình học.

Lời giải chi tiết:

Phân tích các lực tác dụng lên quả cầu:

Khi quả cầu cân bằng thì: \(\overrightarrow P  + \overrightarrow T  + \overrightarrow {{F_d}}  = 0\)

Đặt \(\overrightarrow {T'}  = \overrightarrow P  + \overrightarrow {{F_d}}  \Rightarrow \overrightarrow {T'}  + \overrightarrow T  = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {T'} \, \uparrow  \downarrow \overrightarrow T \\T' = T\end{array} \right.\)

Hai dây treo hợp với nhau một góc 60⁰\( \Rightarrow \alpha  = {30^0}\)

Từ hình vẽ ta có:

\(\begin{array}{l}\tan \alpha  = \dfrac{{{F_d}}}{P} \Rightarrow {F_d} = P.\tan \alpha  = mg.\tan \alpha \\ \Rightarrow {F_d} = 0,{3.10^{ - 3}}.10.\tan 30 = 1,{73.10^{ - 3}}N\end{array}\)

Chọn B.

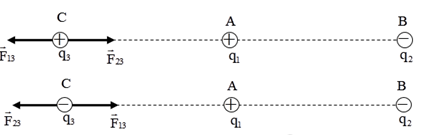
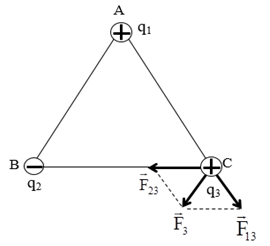
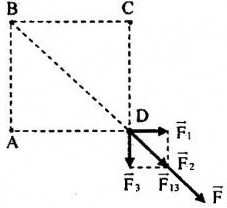
Phương pháp giải:

Hai điện tích trái dấu thì hút nhau, hai điện tích cùng dấu thì đẩy nhau

Công thức tính lực tương tác: \(F = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Công thức tổng hợp lực: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Lời giải chi tiết:

Gọi \(\overrightarrow {{F_{13}}} ;\overrightarrow {{F_{23}}} \) lần lượt là lực do q₁, q₂ tác dụng lên q₃

Để q₃ cân bằng \( \Rightarrow \overrightarrow {{F_{13}}}  + \overrightarrow {{F_{23}}}  = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{F_{13}}} \, \uparrow  \downarrow \,\overrightarrow {{F_{23}}} \,\,\,\left( 1 \right)\\{F_{13}} = {F_{23}}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Do \({q_1};{q_2}\) trái dấu → Để lực tổng hợp tại C bằng 0 thì C nằm ngoài AB và gần A hơn.

\( \Rightarrow CB - CA = AB = 8cm\,{\rm{ }}\left( 1 \right)\)

Lại có: \({F_{13}} = {F_{23}} \Leftrightarrow \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{C{A^2}}} = \dfrac{{k\left| {{q_2}{q_3}} \right|}}{{C{B^2}}}\)

\( \Rightarrow \dfrac{{CA}}{{CB}} = \sqrt {\left| {\dfrac{{{q_1}}}{{{q_2}}}} \right|}  = \dfrac{1}{2} \Rightarrow CB = 2.CA\,\,\,\left( 1 \right)\)

Từ (1) và (2) \( \Rightarrow \left\{ \begin{array}{l}CA = 8cm\\CB = 16cm\end{array} \right.\)

Chọn A

Phương pháp giải:

Sử dụng biểu thức định luật Cu-lông: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Lời giải chi tiết:

+ Khi hai điện tích đặt cách nhau khoảng \(d\): \({F_1} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{d^2}}}\)

+ Khi hai điện tích đặt cách nhau khoảng \(d + 0,1\): \({F_2} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{{\left( {d + 0,1} \right)}^2}}}\)

\(\begin{array}{l} \Rightarrow \dfrac{{{F_1}}}{{{F_2}}} = \dfrac{{{{\left( {d + 0,1} \right)}^2}}}{{{d^2}}}\\ \Leftrightarrow \dfrac{{{{2.10}^{ - 6}}}}{{{{5.10}^{ - 7}}}} = \dfrac{{{{\left( {d + 0,1} \right)}^2}}}{{{d^2}}}\\ \Rightarrow \dfrac{{d + 0,1}}{d} = 2\\ \Rightarrow d = 0,1m = 10cm\end{array}\)

Chọn C

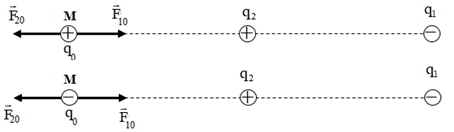
Phương pháp giải:

Để \({q_0}\) cân bằng thì: \(\overrightarrow {{F_{10}}}  + \overrightarrow {{F_{20}}}  = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{F_{10}}} \, \uparrow  \downarrow \,\overrightarrow {{F_{20}}} \,\,\,\left( 1 \right)\\{F_{10}} = {F_{20}}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Giải (1) \( \Rightarrow \) ba điện tích thẳng hàng

+ Nếu \({q_1};{q_2}\) cùng dấu \( \Rightarrow \) q₀ nằm trong q₁ và q₂.

(Không phụ thuộc vào dấu của q₀)

+ Nếu \({q_1};{q_2}\) trái dấu \( \Rightarrow \) q₀ nằm ngoài q₁ và q₂ và gần điện tích có độ lớn nhỏ hơn.

(Không phụ thuộc vào dấu của q₀)

Lời giải chi tiết:

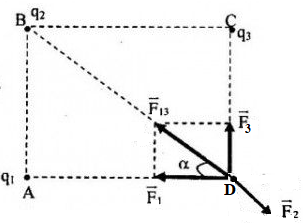
Để q₃ cân bằng \( \Rightarrow \overrightarrow {{F_{13}}}  + \overrightarrow {{F_{23}}}  = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{F_{13}}} \, \uparrow  \downarrow \,\overrightarrow {{F_{23}}} \,\,\,\left( 1 \right)\\{F_{13}} = {F_{23}}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Do \({q_1};{q_2}\) cùng dấu → Để lực tổng hợp tại C bằng 0 thì C nằm trên đường nối q₁, q₂ và nằm trong khoảng q₁, q₂ \( \Rightarrow AC + BC = AB = 9cm\,\,\,\left( * \right)\)

Lại có: \({F_{13}} = {F_{23}} \Leftrightarrow \dfrac{{k\left| {{q_1}{q_3}} \right|}}{{A{C^2}}}\, = \,\dfrac{{k\left| {{q_2}{q_3}} \right|}}{{B{C^2}}}\)

\( \Leftrightarrow \dfrac{{\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}}\, = \dfrac{{A{C^2}}}{{B{C^2}}} = \dfrac{1}{4} \Rightarrow BC = 2.AC\,\,\,\left( {**} \right)\)

Từ (*) và (**) ta có: \(\left\{ \begin{array}{l}AC + BC = 9\,\\BC = 2.AC\end{array} \right. \Rightarrow \left\{ \begin{array}{l}AC = 3cm\\BC = 6cm\end{array} \right.\)

Vậy \({q_3}\) đặt giữa hai điện tích cách q₁ khoảng 3cm và cách q₂ khoảng 6cm

Chọn B.

Phương pháp giải:

Để \({q_0}\) cân bằng thì: \(\overrightarrow {{F_{10}}}  + \overrightarrow {{F_{20}}}  = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{F_{10}}} \, \uparrow  \downarrow \,\overrightarrow {{F_{20}}} \,\,\,\left( 1 \right)\\{F_{10}} = {F_{20}}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Giải (1) \( \Rightarrow \) ba điện tích thẳng hàng

+ Nếu \({q_1};{q_2}\) cùng dấu \( \Rightarrow \) q₀ nằm trong q₁ và q₂.

(Không phụ thuộc vào dấu của q₀)

+ Nếu \({q_1};{q_2}\) trái dấu \( \Rightarrow \) q₀ nằm ngoài q₁ và q₂ và gần điện tích có độ lớn nhỏ hơn.

(Không phụ thuộc vào dấu của q₀)

Lời giải chi tiết:

Để q₀ cân bằng thì \(\overrightarrow {{F_{10}}}  + \overrightarrow {{F_{20}}}  = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{F_{10}}} \, \uparrow  \downarrow \,\overrightarrow {{F_{20}}} \,\,\,\left( 1 \right)\\{F_{10}} = {F_{20}}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Do \({q_1};{q_2}\) trái dấu nên C q₀ nằm ngoài khoảng q₁, q₂ và gần q₂ hơn.

\( \Rightarrow {r_1} - {r_2} = d\,\,\,\left( * \right)\)

Lại có: \({F_{10}} = {F_{20}} \Leftrightarrow \dfrac{{k\left| {{q_1}{q_0}} \right|}}{{r_1^2}}\, = \,\dfrac{{k\left| {{q_2}{q_0}} \right|}}{{r_2^2}}\)

\( \Leftrightarrow \dfrac{{\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}}\, = \dfrac{{r_1^2}}{{r_2^2}} = 9 \Leftrightarrow \dfrac{{{r_1}}}{{{r_2}}} = 3 \Rightarrow {r_1} = 3{r_2}\,\,\left( {**} \right)\)

Từ (*) và (**) ta có: \(\left\{ \begin{array}{l}{r_1} - {r_2} = d\,\\{r_1} = 3{r_2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{r_1} = \dfrac{{3d}}{2}\\{r_2} = \dfrac{d}{2}\end{array} \right.\)

Vậy \({q_0}\) tùy ý đặt cách q₁ khoảng \(\dfrac{{3d}}{2}\)

Chọn B.

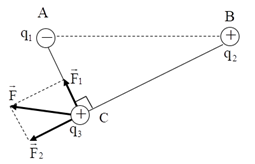
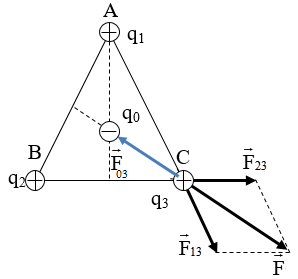
Phương pháp giải:

Công thức tính lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Hợp lực tác dụng lên điện tích: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Vẽ hình. Sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Điện tích q₃ sẽ chịu hai lực tác dụng của q₁ và q₂ là:\(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} \)

Lực tổng hợp tác dụng lên q₃ là: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Ta có: \(\left\{ \begin{array}{l}AB = 20cm\\AC = 12cm\\BC = 16cm\end{array} \right. \Rightarrow \Delta ACB\) vuông tại C.

Biểu diễn các lực trên hình vẽ:

Từ hình vẽ ta có: \(\overrightarrow {{F_1}}  \bot \overrightarrow {{F_2}}  \Rightarrow F = \sqrt {F_1^2 + F_2^2} \)

Với: \(\left\{ \begin{array}{l}{F_1} = \dfrac{{k.\left| {{q_1}{q_3}} \right|}}{{A{C^2}}} = \dfrac{{{{9.10}^9}.\left| { - {{3.10}^{ - 6}}{{.2.10}^{ - 6}}} \right|}}{{0,{{12}^2}}} = 3,75N\\{F_2} = \dfrac{{k.\left| {{q_2}{q_3}} \right|}}{{B{C^2}}} = \dfrac{{{{9.10}^9}.\left| {{{8.10}^{ - 6}}{{.2.10}^{ - 6}}} \right|}}{{0,{{16}^2}}} = 5,625N\end{array} \right.\)

\( \Rightarrow F = \sqrt {F_1^2 + F_2^2}  = \sqrt {{{\left( {3,75} \right)}^2} + {{\left( {5,625} \right)}^2}}  = 6,76N\)

Chọn A.

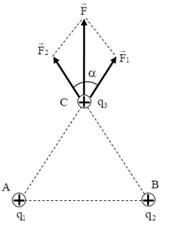
Phương pháp giải:

Công thức tính lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Hợp lực tác dụng lên điện tích: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Vẽ hình. Sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Điện tích q₃ sẽ chịu hai lực tác dụng của q₁ và q₂ là:\(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} \)

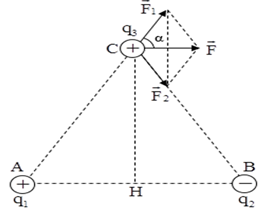
Lực tổng hợp tác dụng lên q₃ là: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Biểu diễn các lực tác dụng vào q₃ như hình vẽ:

Với: \(\left\{ \begin{array}{l}{F_1} = \dfrac{{k.\left| {{q_1}{q_3}} \right|}}{{A{C^2}}} = \dfrac{{{{9.10}^9}.\left| {{{4.10}^{ - 10}}{{.3.10}^{ - 12}}} \right|}}{{0,{1^2}}} = 1,{08.10^{ - 9}}N\\{F_2} = \dfrac{{k.\left| {{q_2}{q_3}} \right|}}{{B{C^2}}} = \dfrac{{{{9.10}^9}.\left| {{{4.10}^{ - 10}}{{.3.10}^{ - 12}}} \right|}}{{0,{1^2}}} = 1,{08.10^{ - 9}}N\end{array} \right.\)

Vì tam giác ACB đều nên \(\alpha  = {60^0}\)

\( \Rightarrow F = \sqrt {F_1^2 + F_2^2 + 2.{F_1}{F_2}.cos60}  = 1,08\sqrt 3 {.10^{ - 9}}N = 1,{87.10^{ - 9}}N\)  

Chọn D.

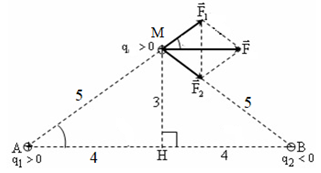
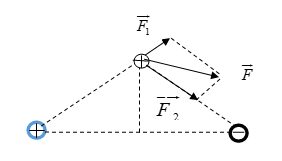
Phương pháp giải:

Công thức tính lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Hợp lực tác dụng lên điện tích: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Vẽ hình. Sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Biểu diễn các lực của \({q_1};{q_2}\)tác dụng lên \({q_3}\) như hình vẽ:

Ta có: \({F_1} = {F_2} = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = \dfrac{{{{9.10}^9}{{.2.10}^{ - 6}}{{.2.10}^{ - 6}}}}{{0,{{03}^2} + 0,{{04}^2}}} = 14,4N\)

\( \Rightarrow {F_1} = {F_2} \Rightarrow \) hình bình hành là hình thoi

\( \Rightarrow \overrightarrow F \) nằm trên phân giác của \(\left( {\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} } \right)\)

\( \Rightarrow \overrightarrow F  \bot MH\) (phân giác của hai góc kề bù) \( \Rightarrow \overrightarrow F \,//\,AB\)

\( \Rightarrow \left( {\overrightarrow {{F_1}} ;\overrightarrow F } \right) = \widehat {MAB}\)

\(\begin{array}{l} \Rightarrow F = 2.{F_1}.cos\left( {\overrightarrow {{F_1}} ;\overrightarrow F } \right) = 2.{F_1}.cos\widehat {MAB} = 2.{F_1}.\dfrac{{AH}}{{AM}}\\ \Rightarrow F = 2.14,4.\dfrac{4}{5} = 23,04N\end{array}\)

Chọn C.

Phương pháp giải:

Áp dụng biểu thức tính lực tương tác tĩnh điện: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Lời giải chi tiết:

+ Khi khoảng cách giữa hai điện tích r: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = {2.10^{ - 6}}N\)

+ Khi đưa chúng ra xa nhau thêm 2cm: r’ = r + 0,02: 

\(\begin{array}{l}
F' = \frac{{k\left| {{q_1}{q_2}} \right|}}{{r{'^2}}} = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{{(r + 0,02)}^2}}} = {5.10^{ - 7}}N\\
\Rightarrow \frac{F}{{F'}} = \frac{{{{(r + 0,02)}^2}}}{{{r^2}}} = \frac{{{{2.10}^{ - 6}}}}{{{{5.10}^{ - 7}}}} = 4\\
\Rightarrow r + 0,02 = 2{\rm{r}} \Rightarrow r = 0,02m = 2cm
\end{array}\)

Chọn B.

Phương pháp giải:

Công thức tính lực tương tác: \(F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Lời giải chi tiết:

Lực tương tác giữa hai điện tích đặt trong không khí và trong điện môi là:

\(\left\{ \begin{array}{l}F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = {2.10^{ - 3}}\\{F_\varepsilon } = \frac{{k\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} = {10^{ - 3}}\end{array} \right. \Rightarrow \frac{F}{{{F_\varepsilon }}} = \varepsilon  = 2 \Rightarrow \varepsilon  = 2\)

Để lực tương tác giữa hai điện tích khi đặt trong điện môi bằng lực tương tác giữa hai điện tích khi ta đặt trong không khí thì khoảng cách giữa hai điện tích bây giờ là r'

\(\left\{ \begin{array}{l}F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\\{F_\varepsilon } = \frac{{k\left| {{q_1}{q_2}} \right|}}{{\varepsilon r{'^2}}}\end{array} \right. \Rightarrow F = {F_\varepsilon } \Rightarrow \frac{1}{{{r^2}}} = \frac{1}{{\varepsilon r{'^2}}} \Rightarrow r' = \frac{r}{{\sqrt \varepsilon  }} = 10\sqrt 2 cm\)

Chọn B.

Phương pháp giải:

Hai điện tích trái dấu thì hút nhau, hai điện tích cùng dấu thì đẩy nhau

Công thức tính lực tương tác: \(F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Công thức tổng hợp lực: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Lời giải chi tiết:

Vì C cách đều A, B nên C nằm trên đường trung trực của đoạn AB.

Ta có: \(\left\{ \begin{array}{l}{F_1} = \frac{{k\left| {{q_1}{q_3}} \right|}}{{A{C^2}}} = 23,{04.10^{ - 3}}N\\{F_2} = \frac{{k\left| {{q_2}{q_3}} \right|}}{{C{B^2}}} = 23,{04.10^{ - 3}}N\end{array} \right.\)

Vì F₁ = F₂  nên \(\overrightarrow F \) nằm trên đường phân giác góc và \(\widehat {\left( {\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} } \right)} \Rightarrow \overrightarrow F  \bot CH\) (phân giác của hai góc kề bù)

\( \Rightarrow \overrightarrow F //AB \Rightarrow \alpha  = \widehat {\left( {\overrightarrow {{F_1}} ,\overrightarrow F } \right)} = \widehat {CAB}\)

Độ lớn lực tổng hợp : \(F = 2.{F_1}.\cos \alpha  = 2.{F_1}.\frac{{AH}}{{AC}} = 2.23,{04.10^{ - 3}}.\frac{3}{5} = 27,{648.10^{ - 3}}N\)

Chọn B

Phương pháp giải:

Phương pháp:

Hai điện tích trái dấu thì hút nhau, hai điện tích cùng dấu thì đẩy nhau

Công thức tính lực tương tác: \(F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Công thức tổng hợp lực: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Lời giải chi tiết:

Cách giải:

Ta có: \(\overrightarrow {{F_3}}  = \overrightarrow {{F_{13}}}  + \overrightarrow {{F_{23}}} \)

Với: \(\left\{ \begin{array}{l}{F_{13}} = \frac{{k\left| {{q_1}{q_3}} \right|}}{{{a^2}}}\\{F_{23}} = \frac{{k\left| {{q_2}{q_3}} \right|}}{{{a^2}}}\\\left| {{q_1}} \right| = \left| {{q_2}} \right|\\\alpha  = {120^0}\end{array} \right. \Rightarrow {F_3} = {F_{13}} = {F_{23}} = \frac{{{{9.10}^9}.\left| {{{4.10}^{ - 8}}{{.5.10}^{ - 8}}} \right|}}{{{{\left( {{{2.10}^{ - 2}}} \right)}^2}}} = {45.10^{ - 3}}N\)

Chọn D

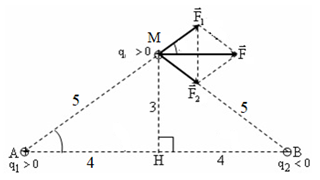
Phương pháp giải:

Áp dụng công thức Cu lông tính lực điện \(F = k.\frac{{|{q_1}.{q_2}|}}{{{r^2}}}\)

Vẽ hình. Sau đó ta tổng hợp vec to lực F tác dụng lên hạt điện tích điểm q theo quy tắc hình bình hành và tính lực tổng hợp.

Lời giải chi tiết:

Tóm tắt:

\({q_1} = {10^{ - 8}}C;{q_2} = - {3.10^{ - 8}}C;d = 8cm;k = {9.10^9}N{m^2}/{C^2}\)

Đặt \(q = {10^{ - 8}}C\) tại điểm M trên đường trung trực của đoạn thẳng AB và cách AB một khoảng 3cm.

F = ?

Giải:

Ta có hình vẽ:

Ta có :  

\(\left\{ \begin{array}{l}
{F_1} = k.\frac{{\left| {{q_1}.q} \right|}}{{{r^2}}} = {9.10^9}.\frac{{\left| {{{10}^{ - 8}}{{.10}^{ - 8}}} \right|}}{{0,{{05}^2}}} = 3,{6.10^{ - 4}}N\\
{F_2} = k.\frac{{\left| {{q_2}.q} \right|}}{{{r^2}}} = {9.10^9}.\frac{{\left| { - {{3.10}^{ - 8}}{{.10}^{ - 8}}} \right|}}{{0,{{05}^2}}} = 10,{8.10^{ - 4}}N
\end{array} \right.\)

Góc tạo bởi hai vecto lực là  

\(\alpha = {180^0} - 2.\left( {\arctan \frac{4}{3}} \right) = {73^0}44'\)

Độ lớn của lực tổng hợp là: 

\(F = \sqrt {F_1^2 + F_2^2 + 2.{F_1}.{F_2}.\cos \alpha } = 12,{3.10^{ - 4}}N = 1,{23.10^{ - 3}}N\)

Chọn B

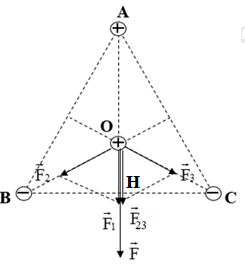
Phương pháp giải:

Công thức tính lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Hợp lực tác dụng lên điện tích: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Vẽ hình. Sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Điện tích q sẽ chịu hai lực tác dụng của q₁ và q₂ là:\(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} \)

Lực tổng hợp tác dụng lên q là: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \)

Biểu diễn các lực tác dụng vào M trên hình vẽ:

Gọi\(\,\alpha  = \left( {\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} } \right)\)

Với: \(\left\{ \begin{array}{l}{F_1} = \dfrac{{k.\left| {{q_1}q} \right|}}{{A{M^2}}} = \dfrac{{{{9.10}^9}.\left| {{{3.10}^{ - 8}}{{.10}^{ - 8}}} \right|}}{{0,{{05}^2}}} = 1,{08.10^{ - 3}}N\\{F_2} = \dfrac{{k.\left| {{q_2}q} \right|}}{{B{M^2}}} = \dfrac{{{{9.10}^9}.\left| { - {{2.10}^{ - 8}}{{.10}^{ - 8}}} \right|}}{{0,{{05}^2}}} = 0,{72.10^{ - 3}}N\end{array} \right.\)

Từ hình vẽ ta có:

\(\sin AMH = \dfrac{4}{5} \Rightarrow \widehat {AMH} = 53,{13^0} \Rightarrow \alpha  = 180 - 2.\widehat {AMH} = 73,{74^0}\)

\( \Rightarrow F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}\cos \alpha }  = 1,{46.10^{ - 3}}N\)

Chọn C.

Phương pháp giải:

+ Lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

+ Hai điện tích cùng dấu thì đẩy nhau, hai điện tích trái dấu thì hút nhau.

+ Lực tổng hợp tác dụng lên điện tích điểm: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

+ Vẽ hình, sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Biểu diễn các lực tác dụng lên q₀ như hình vẽ:

Gọi H là chân đường cao kẻ từ A xuống BC. Ta có:

\(OA = \dfrac{2}{3}AH = \dfrac{2}{3}.\sqrt {A{B^2} - B{H^2}}  = \dfrac{2}{3}.\sqrt {{24^2} - {12^2}}  = 8\sqrt 3 cm\)

Lực tác dụng lên q₀: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

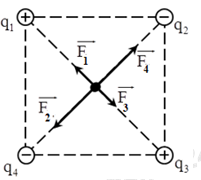
Ta thấy: \(\left\{ \begin{array}{l}\left| {{q_{1\;}}} \right| = \left| {{q_{2\;}}} \right| = \left| {{q_{3\;}}} \right| = {9.10^{ - 8}}C\\OA = OB = OC = 8\sqrt 3 cm\end{array} \right. \Rightarrow {F_1} = {F_2} = {F_3}\)

Ta có: \(\overrightarrow {{F_{23}}}  = \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

Từ hình vẽ ta thấy hình bình hành tạo bởi \(\overrightarrow {{F_2}} \) và \(\overrightarrow {{F_3}} \) là hình thoi và \(\left( {\overrightarrow {{F_2}} ;\overrightarrow {{F_3}} } \right) = {60^0}\)

\(\begin{array}{l} \Rightarrow {F_{23}} = 2{F_2}.cos60 = {F_2}\\ \Rightarrow {F_{23}} = \dfrac{{k.\left| {{q_0}{q_2}} \right|}}{{O{B^2}}} = \dfrac{{{{9.10}^9}.\left| {\left( { - {{9.10}^{ - 8}}} \right){{.5.10}^{ - 8}}} \right|}}{{{{\left( {8\sqrt 3 {{.10}^{ - 2}}} \right)}^2}}} = 2,{11.10^{ - 3}}N\end{array}\)

Ta có: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_{23}}} \)

Mà \(\overrightarrow {{F_1}}  \uparrow  \uparrow \overrightarrow {{F_{23}}}  \Rightarrow F = {F_1} + {F_{23}} = 2.{F_{23}} = 4,{22.10^{ - 3}}N\)

Chọn A.

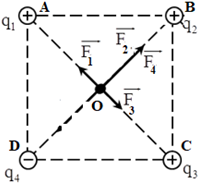
Phương pháp giải:

+ Lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

+ Hai điện tích cùng dấu thì đẩy nhau, hai điện tích trái dấu thì hút nhau.

+ Lực tổng hợp tác dụng lên điện tích điểm: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

+ Vẽ hình, sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Biểu diễn các lực tác dụng lên q₄ như hình vẽ:

Ta có: \(\left\{ \begin{array}{l}\left| {{q_{1\;}}} \right| = \left| {{q_{2\;}}} \right| = \left| {{q_{3\;}}} \right| = \left| {{q_4}} \right| = {2.10^{ - 8}}C\\AB = BC = CD = DA = 4cm\\BD = \sqrt {A{B^2} + A{D^2}}  = \sqrt {{4^2} + {4^2}}  = 4\sqrt 2 cm\end{array} \right. \Rightarrow {F_1} = {F_3}\)

Lực tác dụng lên q₄: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

Với: \(\left\{ \begin{array}{l}{F_1} = {F_3} = \dfrac{{k.\left| {{q_1}{q_4}} \right|}}{{A{D^2}}} = \dfrac{{{{9.10}^9}.{{\left( {{{2.10}^{ - 8}}} \right)}^2}}}{{{{\left( {{{4.10}^{ - 2}}} \right)}^2}}} = 2,{25.10^{ - 3}}N\\{F_2} = \dfrac{{k.\left| {{q_2}{q_4}} \right|}}{{B{D^2}}} = \dfrac{{{{9.10}^9}.{{\left( {{{2.10}^{ - 8}}} \right)}^2}}}{{{{\left( {4\sqrt 2 {{.10}^{ - 2}}} \right)}^2}}} = 1,{125.10^{ - 3}}N\end{array} \right.\)

Ta có: \(\overrightarrow {{F_{13}}}  = \overrightarrow {{F_1}}  + \overrightarrow {{F_3}} \)

Vì \(\overrightarrow {{F_1}}  \bot \overrightarrow {{F_3}}  \Rightarrow {F_{13}} = \sqrt {F_1^2 + F_3^2}  = {F_1}\sqrt 2  = 2,25\sqrt 2 {.10^{ - 3}}N\)

Ta có: \(\overrightarrow F  = \overrightarrow {{F_2}}  + \overrightarrow {{F_{13}}} \)

Mà \(\overrightarrow {{F_2}}  \uparrow  \uparrow \overrightarrow {{F_{13}}}  \Rightarrow F = {F_2} + {F_{23}} = 4,{31.10^{ - 3}}N\)

Chọn D.

Phương pháp giải:

+ Lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

+ Hai điện tích cùng dấu thì đẩy nhau, hai điện tích trái dấu thì hút nhau.

+ Lực tổng hợp tác dụng lên điện tích điểm: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

+ Vẽ hình, sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Biểu diễn các lực tác dụng lên q₄ như hình vẽ:

Ta có: \(\left\{ \begin{array}{l}\left| {{q_{1\;}}} \right| = \left| {{q_{2\;}}} \right| = \left| {{q_{3\;}}} \right| = \left| {{q_4}} \right| = {2.10^{ - 8}}C\\AB = BC = CD = DA = 4cm\\BD = \sqrt {A{B^2} + A{D^2}}  = \sqrt {{4^2} + {4^2}}  = 4\sqrt 2 cm\end{array} \right. \Rightarrow {F_1} = {F_3}\)

Lực tác dụng lên q₄: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

Với: \(\left\{ \begin{array}{l}{F_1} = {F_3} = \dfrac{{k.\left| {{q_1}{q_4}} \right|}}{{A{D^2}}} = \dfrac{{{{9.10}^9}.{{\left( {{{2.10}^{ - 8}}} \right)}^2}}}{{{{\left( {{{4.10}^{ - 2}}} \right)}^2}}} = 2,{25.10^{ - 3}}N\\{F_2} = \dfrac{{k.\left| {{q_2}{q_4}} \right|}}{{B{D^2}}} = \dfrac{{{{9.10}^9}.{{\left( {{{2.10}^{ - 8}}} \right)}^2}}}{{{{\left( {4\sqrt 2 {{.10}^{ - 2}}} \right)}^2}}} = 1,{125.10^{ - 3}}N\end{array} \right.\)

Ta có: \(\overrightarrow {{F_{13}}}  = \overrightarrow {{F_1}}  + \overrightarrow {{F_3}} \)

Vì \(\overrightarrow {{F_1}}  \bot \overrightarrow {{F_3}}  \Rightarrow {F_{13}} = \sqrt {F_1^2 + F_3^2}  = {F_1}\sqrt 2  = 2,25\sqrt 2 {.10^{ - 3}}N\)

Ta có: \(\overrightarrow F  = \overrightarrow {{F_2}}  + \overrightarrow {{F_{13}}} \)

Mà \(\overrightarrow {{F_2}}  \uparrow  \downarrow \overrightarrow {{F_{13}}} \)

\( \Rightarrow F = \left| {{F_2} - {F_{23}}} \right| = \left| {1,{{125.10}^{ - 3}} - 2,25\sqrt 2 {{.10}^{ - 3}}} \right| = 2,{06.10^{ - 3}}N\)

Chọn B.

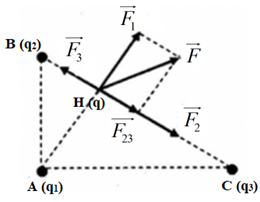
Phương pháp giải:

+ Lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

+ Hai điện tích cùng dấu thì đẩy nhau, hai điện tích trái dấu thì hút nhau.

+ Lực tổng hợp tác dụng lên điện tích điểm: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

+ Vẽ hình, sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Biểu diễn các lực tác dụng lên q₄ như hình vẽ:

Áp dụng hệ thức lượng trong tam giác vuông:

\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} = \dfrac{1}{{{{60}^2}}} + \dfrac{1}{{{{80}^2}}} \Rightarrow AH = 48cm\)

Áp dụng định lí Pi-ta-go ta có:

\(\left\{ \begin{array}{l}BH = \sqrt {A{B^2} - A{H^2}}  = \sqrt {{{60}^2} - {{48}^2}}  = 36cm\\CH = \sqrt {A{C^2} - A{H^2}}  = \sqrt {{{80}^2} - {{48}^2}}  = 64cm\end{array} \right.\)

Lực tổng hợp tác dụng lên q: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

Với: \(\left\{ \begin{array}{l}{F_1} = \dfrac{{k.\left| {{q_1}q} \right|}}{{A{H^2}}} = \dfrac{{{{9.10}^9}.\left| {{{10}^{ - 6}}{{.2.10}^{ - 8}}} \right|}}{{0,{{48}^2}}} = 7,{8.10^{ - 4}}N\\{F_2} = \dfrac{{k.\left| {{q_2}q} \right|}}{{B{H^2}}} = \dfrac{{{{9.10}^9}.\left| {{{10}^{ - 6}}{{.2.10}^{ - 8}}} \right|}}{{0,{{36}^2}}} = 1,{4.10^{ - 3}}N\\{F_3} = \dfrac{{k.\left| {{q_3}q} \right|}}{{C{H^2}}} = \dfrac{{{{9.10}^9}.\left| {{{10}^{ - 6}}{{.2.10}^{ - 8}}} \right|}}{{0,{{64}^2}}} = 4,{4.10^{ - 4}}N\end{array} \right.\)

Ta có: \(\overrightarrow {{F_{23}}}  = \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

Ta thấy: \(\overrightarrow {{F_2}}  \uparrow  \downarrow \overrightarrow {{F_3}}  \Rightarrow {F_{23}} = \left| {{F_2} - {F_3}} \right| = 9,{6.10^{ - 4}}N\)

Lực tổng hợp: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_{23}}} \)

Vì \(\overrightarrow {{F_1}}  \bot \overrightarrow {{F_{23}}}  \Rightarrow F = \sqrt {F_1^2 + F_{23}^2}  = 12,{4.10^{ - 4}}N\)

Chọn C.

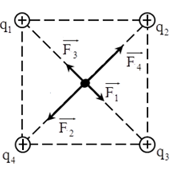
Phương pháp giải:

+ Lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

+ Hai điện tích cùng dấu thì đẩy nhau, hai điện tích trái dấu thì hút nhau.

+ Lực tổng hợp tác dụng lên điện tích điểm: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

+ Vẽ hình, sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Biểu diễn các lực tác dụng lên q₀ như hình vẽ:

Lực tổng hợp tác dụng lên q₀: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + \overrightarrow {{F_4}} \)

Ta có: \(\left\{ \begin{array}{l}{q_{1\;}} = {q_{2\;}} = {q_{3\;}} = {q_4}\\OA = OB = OC = OD\end{array} \right. \Rightarrow {F_1} = {F_2} = {F_3} = {F_4}\)

Mặt khác: \(\left\{ \begin{array}{l}\overrightarrow {{F_1}}  \uparrow  \downarrow \overrightarrow {{F_3}}  \Rightarrow {F_{13}} = \left| {{F_1} - {F_3}} \right| = 0\\\overrightarrow {{F_2}}  \uparrow  \downarrow \overrightarrow {{F_4}}  \Rightarrow {F_{24}} = \left| {{F_2} - {F_4}} \right| = 0\end{array} \right. \Rightarrow \overrightarrow F  = \overrightarrow {{F_{13}}}  + \overrightarrow {{F_{24}}}  = 0\)

Chọn D.

Phương pháp giải:

+ Lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

+ Hai điện tích cùng dấu thì đẩy nhau, hai điện tích trái dấu thì hút nhau.

+ Lực tổng hợp tác dụng lên điện tích điểm: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

+ Vẽ hình, sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Biểu diễn các lực tác dụng lên q₀ như hình vẽ:

Lực tổng hợp tác dụng lên q₀: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + \overrightarrow {{F_4}} \)

Lực tương tác giữa hai điện tích được xác định bởi công thức: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

Ta có: \(\left\{ \begin{array}{l}\left| {{q_{1\;}}} \right| = \left| {{q_{2\;}}} \right| = \left| {{q_{3\;}}} \right| = \left| {{q_4}} \right|\\OA = OB = OC = OD\end{array} \right. \Rightarrow {F_1} = {F_2} = {F_3} = {F_4}\)

Mặt khác: \(\left\{ \begin{array}{l}\overrightarrow {{F_1}}  \uparrow  \downarrow \overrightarrow {{F_3}}  \Rightarrow {F_{13}} = \left| {{F_1} - {F_3}} \right| = 0\\\overrightarrow {{F_2}}  \uparrow  \downarrow \overrightarrow {{F_4}}  \Rightarrow {F_{24}} = \left| {{F_2} - {F_4}} \right| = 0\end{array} \right. \Rightarrow \overrightarrow F  = \overrightarrow {{F_{13}}}  + \overrightarrow {{F_{24}}}  = 0\)

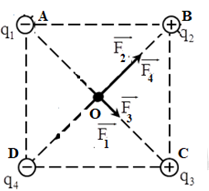
Chọn D.

Phương pháp giải:

+ Lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

+ Hai điện tích cùng dấu thì đẩy nhau, hai điện tích trái dấu thì hút nhau.

+ Lực tổng hợp tác dụng lên điện tích điểm: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

+ Vẽ hình, sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Biểu diễn các lực tác dụng lên q₀ như hình vẽ:

Áp dụng định lí Pitago ta có:

\(OA = \dfrac{{AC}}{2} = \dfrac{{\sqrt {A{D^2} + C{D^2}} }}{2} = \dfrac{{\sqrt {{5^2} + {5^2}} }}{2} = 2,5\sqrt 2 cm\)

Lực tổng hợp tác dụng lên q₀: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + \overrightarrow {{F_4}} \)

Lực tương tác giữa hai điện tích được xác định bởi công thức: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

Ta có: \(\left\{ \begin{array}{l}\left| {{q_{1\;}}} \right| = \left| {{q_{2\;}}} \right| = \left| {{q_{3\;}}} \right| = \left| {{q_4}} \right|\\OA = OB = OC = OD = 2,5\sqrt 2 cm\end{array} \right. \Rightarrow {F_1} = {F_2} = {F_3} = {F_4}\)

Mặt khác: \(\left\{ \begin{array}{l}\overrightarrow {{F_1}}  \uparrow  \downarrow \overrightarrow {{F_3}}  \Rightarrow {F_{13}} = \left| {{F_1} - {F_3}} \right| = 0\\\overrightarrow {{F_2}}  \uparrow  \uparrow \overrightarrow {{F_4}}  \Rightarrow {F_{24}} = {F_2} + {F_4} = 2{F_2}\end{array} \right.\)

\( \Rightarrow F = {F_{24}} = 2{F_2} = 2.\dfrac{{k.\left| {{q_2}{q_0}} \right|}}{{O{B^2}}} = 2.\dfrac{{{{9.10}^9}.\left| {{{4.10}^{ - 6}}.\left( { - {{2.10}^{ - 6}}} \right)} \right|}}{{{{\left( {2,5\sqrt 2 {{.10}^{ - 2}}} \right)}^2}}} = 115,2N\)

Chọn D.

Phương pháp giải:

+ Lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

+ Hai điện tích cùng dấu thì đẩy nhau, hai điện tích trái dấu thì hút nhau.

+ Lực tổng hợp tác dụng lên điện tích điểm: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + \overrightarrow {{F_4}} \)

+ Vẽ hình, sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Biểu diễn các lực tác dụng lên q₀ như hình vẽ:

Áp dụng định lí Pitago ta có:

\(OA = \dfrac{{AC}}{2} = \dfrac{{\sqrt {A{D^2} + C{D^2}} }}{2} = \dfrac{{\sqrt {{5^2} + {5^2}} }}{2} = 2,5\sqrt 2 cm\)

Lực tổng hợp tác dụng lên q₀: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + \overrightarrow {{F_4}} \)

Lực tương tác giữa hai điện tích được xác định bởi công thức: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

Ta có: \(\left\{ \begin{array}{l}\left| {{q_{1\;}}} \right| = \left| {{q_{2\;}}} \right| = \left| {{q_{3\;}}} \right| = \left| {{q_4}} \right|\\OA = OB = OC = OD = 2,5\sqrt 2 cm\end{array} \right. \Rightarrow {F_1} = {F_2} = {F_3} = {F_4}\)

\({F_1} = {F_2} = {F_3} = {F_4} = \dfrac{{k.\left| {{q_1}{q_0}} \right|}}{{O{A^2}}} = \dfrac{{{{9.10}^9}.\left| { - {{4.10}^{ - 8}}.\left( { - {{2.10}^{ - 8}}} \right)} \right|}}{{{{\left( {2,5\sqrt 2 {{.10}^{ - 2}}} \right)}^2}}} = 5,{76.10^{ - 3}}N\)

Mặt khác: \(\left\{ \begin{array}{l}\overrightarrow {{F_1}}  \uparrow  \uparrow \overrightarrow {{F_3}}  \Rightarrow {F_{13}} = {F_1} + {F_3} = 11,{52.10^{ - 3}}N\\\overrightarrow {{F_2}}  \uparrow  \uparrow \overrightarrow {{F_4}}  \Rightarrow {F_{24}} = {F_2} + {F_4} = 11,{52.10^{ - 3}}N\end{array} \right.\)

Lực tổng hợp: \(\overrightarrow F  = \overrightarrow {{F_{13}}}  + \overrightarrow {{F_{24}}} \)

Vì \(\overrightarrow {{F_{13}}}  \bot \overrightarrow {{F_{24}}}  \Rightarrow F = \sqrt {F_{13}^2 + F_{24}^2}  = 11,52\sqrt 2 {.10^{ - 3}}N = 1,{63.10^{ - 2}}N\)

Chọn B.

Phương pháp giải:

+ Lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

+ Hai điện tích cùng dấu thì đẩy nhau, hai điện tích trái dấu thì hút nhau.

+ Lực tổng hợp tác dụng lên điện tích điểm: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

+ Vẽ hình, sử dụng các kiến thức hình học để tính toán.

Lời giải chi tiết:

Biểu diễn các lực tác dụng lên q₀ như hình vẽ:

Gọi H là chân đường cao kẻ từ A xuống BC. Ta có:

\(OA = \dfrac{2}{3}AH = \dfrac{2}{3}.\sqrt {A{B^2} - B{H^2}}  = \dfrac{2}{3}.\sqrt {{6^2} - {3^2}}  = 2\sqrt 3 cm\)

Ta thấy: \(\left\{ \begin{array}{l}\left| {{q_{1\;}}} \right| = {6.10^{ - 9}}C\\\left| {{q_{2\;}}} \right| = \left| {{q_{3\;}}} \right| = {8.10^{ - 9}}C\\OA = OB = OC = 2\sqrt 3 cm\end{array} \right. \Rightarrow {F_2} = {F_3}\)

Lực tổng hợp tác dụng lên q₀: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

Với: \(\left\{ \begin{array}{l}{F_1} = \dfrac{{k.\left| {{q_0}{q_1}} \right|}}{{O{A^2}}} = \dfrac{{{{9.10}^9}.\left| {{{6.10}^{ - 9}}{{.8.10}^{ - 9}}} \right|}}{{{{\left( {2\sqrt 3 {{.10}^{ - 2}}} \right)}^2}}} = 3,{6.10^{ - 4}}N\\{F_2} = {F_3} = \dfrac{{k.\left| {{q_0}{q_2}} \right|}}{{O{B^2}}} = \dfrac{{{{9.10}^9}.\left| {{{8.10}^{ - 9}}.\left( { - {{8.10}^{ - 9}}} \right)} \right|}}{{{{\left( {2\sqrt 3 {{.10}^{ - 2}}} \right)}^2}}} = 4,{8.10^{ - 4}}N\end{array} \right.\)

Ta có: \(\overrightarrow {{F_{23}}}  = \overrightarrow {{F_2}}  + \overrightarrow {{F_3}} \)

Từ hình vẽ ta thấy hình bình hành tạo bởi \(\overrightarrow {{F_2}} \) và \(\overrightarrow {{F_3}} \) là hình thoi và \(\left( {\overrightarrow {{F_2}} ;\overrightarrow {{F_3}} } \right) = {60^0}\)

\( \Rightarrow {F_{23}} = 2{F_2}.cos60 = {F_2} = \dfrac{{k.\left| {{q_0}{q_2}} \right|}}{{O{B^2}}} = 4,{8.10^{ - 4}}N\)

Ta có: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_{23}}} \)

Mà \(\overrightarrow {{F_1}}  \uparrow  \uparrow \overrightarrow {{F_{23}}}  \Rightarrow F = {F_1} + {F_{23}} = 3,{6.10^{ - 4}} + 4,{8.10^{ - 4}} = 8,{4.10^{ - 4}}N\)

Chọn B.

Phương pháp giải:

Để \({q_0}\) cân bằng thì: \(\overrightarrow {{F_{10}}}  + \overrightarrow {{F_{20}}}  = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{F_{10}}} \, \uparrow  \downarrow \,\overrightarrow {{F_{20}}} \,\,\,\left( 1 \right)\\{F_{10}} = {F_{20}}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Giải (1) \( \Rightarrow \) ba điện tích thẳng hàng

+ Nếu \({q_1};{q_2}\) cùng dấu \( \Rightarrow \) q₀ nằm trong q₁ và q₂.

(Không phụ thuộc vào dấu của q₀)

+ Nếu \({q_1};{q_2}\) trái dấu \( \Rightarrow \) q₀ nằm ngoài q₁ và q₂ và gần điện tích có độ lớn nhỏ hơn.

(Không phụ thuộc vào dấu của q₀)

Lời giải chi tiết:

+ Để q₃ cân bằng thì \(\overrightarrow {{F_{13}}}  + \overrightarrow {{F_{23}}}  = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{F_{13}}} \, \uparrow  \downarrow \,\overrightarrow {{F_{23}}} \,\,\,\left( 1 \right)\\{F_{13}} = {F_{23}}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Từ (1) \( \Rightarrow \) A, B, C thẳng hàng.

Do \(\left\{ \begin{array}{l}{q_1}.{q_2} < 0\\\left| {{q_1}} \right|\; < \left| {{q_2}} \right|\;\end{array} \right.\) nên C nằm trong AB và gần q₁ (điểm C) hơn.

\( \Rightarrow BC - AC = AB\, = 15cm\,\,\left( * \right)\)

Từ (2) \( \Rightarrow \dfrac{{\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}}\, = \dfrac{{A{C^2}}}{{B{C^2}}}\, \Rightarrow \dfrac{{AC}}{{BC}} = \sqrt {\dfrac{{{{2.10}^{ - 8}}}}{{3,{{2.10}^{ - 7}}}}}  = \dfrac{1}{4}\,\,\left( {**} \right)\)

Từ (*) và (**) ta có: \(\left\{ \begin{array}{l}BC - AC\, = 15cm\\BC = 4.AC\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}AC = 5cm\\BC = 20cm\end{array} \right.\)

+ Để q₁ cân bằng thì \(\overrightarrow {{F_{21}}}  + \overrightarrow {{F_{31}}}  = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{F_{21}}} \, \uparrow  \downarrow \,\overrightarrow {{F_{31}}} \,\,\,\left( 3 \right)\\{F_{21}} = {F_{31}}\,\,\,\,\,\left( 4 \right)\end{array} \right.\)

Ta có \(\overrightarrow {{F_{21}}} \) hướng sang phải.

Mà từ (3) ta có \(\overrightarrow {{F_{21}}}  \uparrow  \downarrow \overrightarrow {{F_{31}}} \) nên \(\overrightarrow {{F_{31}}} \) hướng sang trái, tức là q₃ hút q₁, do đó điện tích của q₃ < 0.

Từ (4) ta có:

\(\begin{array}{l}\dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{A{B^2}}} = \dfrac{{k.\left| {{q_1}{q_3}} \right|}}{{A{C^2}}} \Rightarrow \dfrac{{\left| {{q_2}} \right|}}{{\left| {{q_3}} \right|}}\, = \dfrac{{A{B^2}}}{{A{C^2}}}\, = \dfrac{{{{15}^2}}}{{{5^2}}} = 9\\ \Rightarrow \left| {{q_3}} \right| = \dfrac{{\left| {{q_2}} \right|}}{9} = \dfrac{{3,{{2.10}^{ - 7}}}}{9} = 3,{56.10^{ - 8}}C \Rightarrow {q_3} =  - 3,{56.10^{ - 8}}C\end{array}\)

Vậy để q₁ cân bằng thì \({q_3} =  - 3,{56.10^{ - 8}}C\)

Làm tương tự với q₂ ta suy ra được để q₂ cân bằng thì \({q_3} =  - 3,{56.10^{ - 8}}C\)

Chọn A.                                

Phương pháp giải:

Để \({q_0}\) cân bằng thì: \(\overrightarrow {{F_{10}}}  + \overrightarrow {{F_{20}}}  = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{F_{10}}} \, \uparrow  \downarrow \,\overrightarrow {{F_{20}}} \,\,\,\left( 1 \right)\\{F_{10}} = {F_{20}}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Giải (1) \( \Rightarrow \) ba điện tích thẳng hàng

+ Nếu \({q_1};{q_2}\) cùng dấu \( \Rightarrow \) q₀ nằm trong q₁ và q₂.

(Không phụ thuộc vào dấu của q₀)

+ Nếu \({q_1};{q_2}\) trái dấu \( \Rightarrow \) q₀ nằm ngoài q₁ và q₂ và gần điện tích có độ lớn nhỏ hơn.

(Không phụ thuộc vào dấu của q₀)

Lời giải chi tiết:

\({q_1}\) đặt tại A, \({q_2}\) đặt tại B, \({q_0}\) tại C

- Gọi lực do \({q_1}\) tác dụng lên \({q_3}\) là \({F_{13}}\);   lực do \({q_2}\) tác dụng lên \({q_3}\) là \({F_{23}}\)

- Để \({q_3}\) nằm cân bằng: \(\overrightarrow {{F_{13}}}  =  - \overrightarrow {{F_{23}}} \)

- Do \({q_1},{q_2}\) cùng dấu \( \Rightarrow {q_0}\) nằm trong khoảng \(AB\)

Lại có : \({F_{10}} = {F_{20}} \Leftrightarrow k\dfrac{{\left| {{q_1}{q_0}} \right|}}{{A{C^2}}} = k\dfrac{{\left| {{q_2}{q_0}} \right|}}{{B{C^2}}}\)

\( \Rightarrow \dfrac{{A{C^2}}}{{B{C^2}}} = \left| {\dfrac{{{q_1}}}{{{q_2}}}} \right| = \dfrac{1}{4} \Rightarrow BC = 2AC\,\,\,\left( 1 \right)\)

Lại có : \(AC + BC = 1cm\) (2)

Từ (1) và (2) ta suy ra : \(\left\{ \begin{array}{l}AC = \dfrac{1}{3}cm\\BC = \dfrac{2}{3}cm\end{array} \right.\)

- Gọi \(\overrightarrow {{F_{01}}} ,\overrightarrow {{F_{21}}} \) lần lượt là lực do \({q_0},{q_2}\) tác dụng lên \({q_1}\)

+ Điều kiện cân bằng của \({q_1}\):

\(\overrightarrow {{F_{01}}}  + \overrightarrow {{F_{21}}}  = \overrightarrow 0 \) \( \Rightarrow \overrightarrow {{F_{01}}}  =  - \overrightarrow {{F_{21}}} \,\,\,\left( 3 \right)\)

\( \Rightarrow \overrightarrow {{F_{01}}} \) ngược chiều \(\overrightarrow {{F_{21}}} \)

Ta suy ra, \({F_{01}}\) là lực hút \( \Rightarrow {q_0} < 0\)

+ Lại có: \({F_{01}} = {F_{21}} \Leftrightarrow k\dfrac{{\left| {{q_0}{q_1}} \right|}}{{A{C^2}}} = k\dfrac{{\left| {{q_2}{q_1}} \right|}}{{A{B^2}}}\)

\( \Rightarrow \left| {{q_0}} \right| = \left| {{q_2}} \right|\dfrac{{A{C^2}}}{{A{B^2}}} = {16.10^{ - 9}}\dfrac{{{{\left( {\dfrac{1}{3}} \right)}^2}}}{{{1^2}}} = \dfrac{{16}}{9}{.10^{ - 9}}C\)

\( \Rightarrow {q_3} =  - \dfrac{{16}}{9}{.10^{ - 9}}C\)  (do lập luận suy ra \({q_0} < 0\) ở trên) (3)

- Gọi \(\overrightarrow {{F_{02}}} ,\overrightarrow {{F_{12}}} \) lần lượt là lực do \({q_0},{q_1}\) tác dụng lên \({q_2}\)

+ Điều kiện cân bằng của \({q_1}\): \(\overrightarrow {{F_{02}}}  + \overrightarrow {{F_{12}}}  = \overrightarrow 0 \) \( \Rightarrow \overrightarrow {{F_{02}}}  =  - \overrightarrow {{F_{12}}} \)

\( \Rightarrow \overrightarrow {{F_{02}}} \) ngược chiều \(\overrightarrow {{F_{12}}} \) \( \Rightarrow {F_{02}}\) là lực hút \( \Rightarrow {q_0} < 0\)

Lại có: \({F_{02}} = {F_{12}} \Leftrightarrow k\dfrac{{\left| {{q_0}{q_2}} \right|}}{{C{B^2}}} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{A{B^2}}}\)

\( \Rightarrow \left| {{q_0}} \right| = \left| {{q_1}} \right|\dfrac{{C{B^2}}}{{A{B^2}}} = {4.10^{ - 9}}\dfrac{{{{\left( {\dfrac{2}{3}} \right)}^2}}}{{{1^2}}} = \dfrac{{16}}{9}{.10^{ - 9}}C\)

\( \Rightarrow {q_3} =  - \dfrac{{16}}{9}{.10^{ - 9}}C\)  (do lập luận suy ra \({q_0} < 0\) ở trên) (4)

Vậy với \({q_3} =  - \dfrac{{16}}{9}{.10^{ - 9}}C\) thì hệ 3 điện tích cân bằng.

Chọn B.

Phương pháp giải:

Để \({q_0}\) cân bằng thì: \(\overrightarrow {{F_{10}}}  + \overrightarrow {{F_{20}}}  = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{F_{10}}} \, \uparrow  \downarrow \,\overrightarrow {{F_{20}}} \,\,\,\left( 1 \right)\\{F_{10}} = {F_{20}}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Giải (1) \( \Rightarrow \) ba điện tích thẳng hàng

+ Nếu \({q_1};{q_2}\) cùng dấu \( \Rightarrow \) q₀ nằm trong q₁ và q₂.

(Không phụ thuộc vào dấu của q₀)

+ Nếu \({q_1};{q_2}\) trái dấu \( \Rightarrow \) q₀ nằm ngoài q₁ và q₂ và gần điện tích có độ lớn nhỏ hơn.

(Không phụ thuộc vào dấu của q₀)

Lời giải chi tiết:

Để q₃ cân bằng thì \(\overrightarrow {{F_{13}}}  + \overrightarrow {{F_{23}}}  + \overrightarrow {{F_{03}}}  = 0\,\,\left( * \right)\)

Đặt \(\overrightarrow F  = \overrightarrow {{F_{13}}}  + \overrightarrow {{F_{23}}} \)

Có: \(\left\{ \begin{array}{l}{q_1} = {q_2}\\AC = BC = a\end{array} \right. \Rightarrow {F_{13}} = {F_{23}} \Rightarrow F = 2{F_{13}}.cos30 = {F_{13}}.\sqrt 3 \)

\(\left( * \right) \Leftrightarrow \overrightarrow F  + \overrightarrow {{F_{03}}}  = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow F  \uparrow  \downarrow \overrightarrow {{F_{03}}} \,\,\,\left( 1 \right)\\F = {F_{03}}\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)

Từ (1) \( \Rightarrow \overrightarrow {{F_{03}}} \) nằm trên đường phân giác của góc \(\widehat {ACB}\) và \({q_0} < 0\)

Làm tương tự với \({q_1};{q_2} \Rightarrow {q_0}\) nằm tại trọng tâm của \(\Delta ABC\) và \({q_0} < 0\)

Từ (2)\( \Rightarrow F = {F_{03}} \Leftrightarrow {F_{13}}\sqrt 3  = {F_{03}} \Leftrightarrow \sqrt 3 .\dfrac{{k.\left| {{q_1}{q_3}} \right|}}{{{a^2}}} = \dfrac{{k.\left| {{q_0}{q_3}} \right|}}{{{{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}}}\)

\( \Leftrightarrow \sqrt 3 .\left| {{q_1}} \right| = 3.\left| {{q_0}} \right| \Rightarrow \left| {{q_0}} \right| = \dfrac{{2\sqrt 3 {{.10}^{ - 6}}}}{{\sqrt 3 }} = {2.10^{ - 6}}C\)

Vậy \({q_0} =  - {2.10^{ - 6}}C\)

Kiểm tra với q₀ thì thấy q₀ cũng cân bằng.

Vậy \({q_0}\) nằm ở trọng tâm của ∆ABC; \({q_0} =  - {2.10^{ - 6}}C\)

Chọn A.

Phương pháp giải:

Định luật Cu – lông \(F = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

Điều kiện cân bằng: \(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + ... + \overrightarrow {{F_n}}  = 0\)

Phân tích các lực tác dụng vào vật trên hình vẽ và sử dụng các kiến thức hình học.

Lời giải chi tiết:

Khi quả cầu cân bằng thì: \(\overrightarrow P  + \overrightarrow T  + \overrightarrow {{F_d}}  = 0\)

Đặt \(\overrightarrow {T'}  = \overrightarrow P  + \overrightarrow {{F_d}}  \Rightarrow \overrightarrow {T'}  + \overrightarrow T  = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {T'} \, \uparrow  \downarrow \overrightarrow T \\T' = T\end{array} \right.\)

Biểu diễn các lực tác dụng lên quả cầu:

+ Từ hình vẽ ta có:

\(\begin{array}{l}\tan \alpha  = \dfrac{{{F_d}}}{P} \Rightarrow {F_d} = P.\tan \alpha  = mg.\tan \alpha \\ \Rightarrow {F_d} = {5.10^{ - 3}}.10.\tan 30 = 0,029N\end{array}\)

+ Khi hai dây treo hợp với nhau một góc 60⁰thì khoảng cách giữa hai điện tích bằng:

\(l = 10cm = 0,1m\)

+ Mà: \(\left\{ \begin{array}{l}F = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\\\left| {{q_1}} \right| = \left| {{q_1}} \right| = \left| q \right|\end{array} \right. \Rightarrow F = k.\dfrac{{{q^2}}}{{{l^2}}} \Rightarrow \left| q \right| = \sqrt {\dfrac{{F.{l^2}}}{k}} \)

Thay số ta được: \(\left| q \right| = \sqrt {\dfrac{{0,029.0,{1^2}}}{{{{9.10}^9}}}}  = 1,{8.10^{ - 7}}C\)

+ Vậy tổng độ lớn điện tích đã truyền cho hai quả cầu là: \(Q = 2.\left| q \right| = 3,{6.10^{ - 7}}\;C\)

Chọn A.

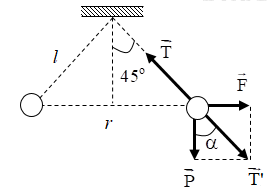
Phương pháp giải:

Định luật Cu – lông \(F = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

Điều kiện cân bằng: \(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  + ... + \overrightarrow {{F_n}}  = 0\)

Phân tích các lực tác dụng vào vật trên hình vẽ và sử dụng các kiến thức hình học.

Lời giải chi tiết:

Khi quả cầu cân bằng thì: \(\overrightarrow P  + \overrightarrow T  + \overrightarrow {{F_d}}  = 0\)

Đặt \(\overrightarrow {T'}  = \overrightarrow P  + \overrightarrow {{F_d}}  \Rightarrow \overrightarrow {T'}  + \overrightarrow T  = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {T'} \, \uparrow  \downarrow \overrightarrow T \\T' = T\end{array} \right.\)

Biểu diễn các lực tác dụng lên quả cầu:

+ Từ hình vẽ ta có:

\(\begin{array}{l}\tan \alpha  = \dfrac{{{F_d}}}{P} \Rightarrow {F_d} = P.\tan \alpha  = mg.\tan \alpha \\ \Rightarrow {F_d} = {5.10^{ - 3}}.10.\tan 45 = 0,05N\end{array}\)

+ Mà: \(\left\{ \begin{array}{l}F = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\\\left| {{q_1}} \right| = \left| {{q_1}} \right| = \left| q \right|\end{array} \right. \Rightarrow F = k.\dfrac{{{q^2}}}{{{r^2}}} \Rightarrow \left| q \right| = \sqrt {\dfrac{{F.{r^2}}}{k}} \)

+ Từ hình vẽ ta có: \(r = 2.\left( {l.\sin 45} \right) = l.\sqrt 2 \)

\( \Rightarrow \left| q \right| = \sqrt {\dfrac{{F.{{\left( {l\sqrt 2 } \right)}^2}}}{k}}  = \sqrt {\dfrac{{0,05.{{\left( {0,3\sqrt 2 } \right)}^2}}}{{{{9.10}^9}}}}  = {10^{ - 6}}C\)

+ Vậy tổng độ lớn điện tích đã truyền cho hai quả cầu là: \(Q = 2\left| q \right| = {2.10^{ - 6}}\;C\)

Chọn B.