30 bài tập số phức mức độ vận dụng, vận dụng caoLàm bàiQuảng cáo
Câu hỏi 1 : Có bao nhiêu số phức z thỏa mãn \(|z+2-i|=2\sqrt{2}\) và \({{(z-1)}^{2}}\) là số thuần ảo?
Đáp án: C Phương pháp giải: Gọi số phức cần tìm là \(z=a+bi\left( a,b\in R \right)\), thay vào các hệ thức trong bài và tìm \(a,b\Rightarrow z\). Số phức \(z=a+bi\) là số thuần ảo nếu \(a=0\). Lời giải chi tiết: Giả sử \(z=a+bi\), ta có \({{(z-1)}^{2}}={{(a+bi-1)}^{2}}={{(a-1)}^{2}}-{{b}^{2}}+2(a-1)bi\). Từ giả thiết \({{(z-1)}^{2}}\) là số thuần ảo suy ra \({(a - 1)^2} - {b^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{b = a - 1}\\{b = 1 - a}\end{array}} \right.\). (1) Từ giả thiết \(|z+2-i|=2\sqrt{2}\) ta có \(|a + bi + 2 - i| = 2\sqrt 2 \Leftrightarrow {(a + 2)^2} + {(b - 1)^2} = 8\) (2) Nếu \(b=a-1\), thay vào (2) có \({{(a+2)}^{2}}+{{(a-2)}^{2}}=8\Leftrightarrow 2{{a}^{2}}+8=8\Leftrightarrow a=0\Rightarrow b=-1\) Nếu \(b=1-a\), thay vào (2) có \({{(a+2)}^{2}}+{{(-a)}^{2}}=8\Leftrightarrow 2{{a}^{2}}+4a-4=0\) (*). Phương trình có \(\Delta '>0\) nên tìm được 2 số phức thỏa mãn. Mặt khác \(a=0\) không là nghiệm của phương trình (*) nên tìm được 3 số phức. Chọn C Câu hỏi 2 : Số phức z thỏa mãn điều kiện \(|z.\bar{z}+z|=2\) và \(|z|=2\) là
Đáp án: B Phương pháp giải: Gọi số phức cần tìm là \(z=x+yi\left( x,y\in R \right)\), thay vào các hệ thức trong bài và tìm \(x,y\Rightarrow z\). Lời giải chi tiết: Với \(z=x+yi\) , thì \(|z|=2\Leftrightarrow {{x}^{2}}+{{y}^{2}}=4\) . (1) Từ \(|z.\bar{z}+z|=2\) ta có: \(|(x+yi)(x-yi)+x+yi|=2\Leftrightarrow |{{x}^{2}}+{{y}^{2}}+x+yi|=2\) \( \Rightarrow |4+x+yi|=2\) Tức là \({{(4+x)}^{2}}+{{y}^{2}}=4\).(2) Từ (1) và (2) suy ra \({{x}^{2}}={{(4+x)}^{2}}\Leftrightarrow -x=4+x\Leftrightarrow x=-2\Rightarrow y=0\Rightarrow z=-2\) Chọn B Câu hỏi 3 : Số phức \(z=x+yi\) thỏa mãn \(|z-2-4i|=|z-2i|\) đồng thời có mô đun nhỏ nhất là:
Đáp án: A Phương pháp giải: Gọi số phức cần tìm là \(z=x+yi\left( x,y\in R \right)\), thay vào các hệ thức trong bài và tìm mối liên hệ \(x,y\). Tìm GTNN của \(\left| z \right|=\sqrt{{{x}^{2}}+{{y}^{2}}}\). Lời giải chi tiết: Từ điều kiện \(|z-2-4i|=|z-2i|\) ta có \(|x+yi-2-4i|=|x+yi-2i| \\ \Leftrightarrow {{(x-2)}^{2}}+{{(y-4)}^{2}}={{x}^{2}}+{{(y-2)}^{2}}\) \(\Leftrightarrow -4x+4-8y+16=-4y+4\Leftrightarrow -4x-4y+16=0 \\ \Leftrightarrow x+y=4\Leftrightarrow x=4-y\) Ta có \(|z|=\sqrt{{{x}^{2}}+{{y}^{2}}}=\sqrt{{{(4-y)}^{2}}+{{y}^{2}}} \\=\sqrt{2{{y}^{2}}-8y+16}=\sqrt{2{{(y-2)}^{2}}+8}\ge 2\sqrt{2}\) Vậy \(\min \left| z \right|=2\sqrt{2}\) khi \(y-2=0\) hay \(y=2\Rightarrow x=2\Rightarrow z=2+2i\). Chọn A Câu hỏi 4 : Số phức z đồng thời thỏa mãn hai điều kiện \(|z-1|=5\) và \(3(z+\bar{z})-z.\bar{z}=0\) là
Đáp án: B Phương pháp giải: Gọi số phức cần tìm là \(z=a+bi\), thay vào các hệ thức trong bài và tìm \(a,b\Rightarrow z\). Lời giải chi tiết: Giả sử \(z=a+bi.\) Từ giả thiết \(|z-1|=5\)) ta có \(|a+bi-1|=5\Leftrightarrow {{(a-1)}^{2}}+{{b}^{2}}=25\Leftrightarrow {{a}^{2}}+{{b}^{2}}-2a=24\) (1) Từ giả thiết \(3(z+\bar{z})-z.\bar{z}=0\) ta có \(3(a+bi+a-bi)-(a+bi).(a-bi)=0\Leftrightarrow 6a-({{a}^{2}}+{{b}^{2}})=0\) (2) Từ (1) có \({{a}^{2}}+{{b}^{2}}=24+2a\) ). Thay vào (2) có \(6a-(24+2a)=0\Leftrightarrow 4a-24=0\Leftrightarrow a=6\) Với \(a=6\) , thay vào (1) có \(36+{{b}^{2}}-12=24\Leftrightarrow {{b}^{2}}=0\Leftrightarrow b=0\Rightarrow z=6\) Chọn B.
Câu hỏi 5 : Tìm số phức z đồng thời thỏa mãn hai điều kiện \(|z+1-2i|=5\) và \(z.\bar{z}=34\).
Đáp án: A Phương pháp giải: Gọi số phức cần tìm là \(z=a+bi\), thay vào các hệ thức trong bài và tìm \(a,b\Rightarrow z\). Lời giải chi tiết: Giả sử \(z=a+bi\). Từ giả thiết \(|z+1-2i|=5\) ta có \(|a + bi + 1 - 2i| = 5 \Leftrightarrow {(a + 1)^2} + {(b - 2)^2} = 25 \Leftrightarrow {a^2} + {b^2} + 2a - 4b = 20\) (1) Từ giả thiết \(z.\bar{z}=34\) ta có \((a + bi).(a - bi) = 34 \Leftrightarrow {a^2} + {b^2} = 34\) (2) Thay (2) vào (1) có \(34 + 2a - 4b = 20 \Leftrightarrow 2a - 4b = - 14 \Leftrightarrow a - 2b = - 7 \Leftrightarrow a = 2b - 7\) Thay vào (2) ta được \({(2b - 7)^2} + {b^2} = 34 \Leftrightarrow 5{b^2} - 28b + 15 = 0 \Leftrightarrow \left[ \begin{array}{l}b = 5\\b = \frac{3}{5}\end{array} \right.\). Với \(b=5\) ta có \(a=3\Rightarrow z=3+5i\) Với \(b=\frac{3}{5}\) ta có \(a=-\frac{29}{5}\Rightarrow z=-\frac{29}{5}+\frac{3}{5}i\) Chọn A Câu hỏi 6 : Giả sử \({{z}_{1}},\,\,{{z}_{2}}\) là hai trong số các số phức \(z\) thỏa mãn \(\left| iz+\sqrt{2}-i \right|=1\) và \(\left| {{z}_{1}}-{{z}_{2}} \right|=2.\) Giá trị lớn nhất của \(\left| {{z}_{1}} \right|+\left| {{z}_{2}} \right|\) bằng
Đáp án: D Phương pháp giải: +) Từ giả thiết \(\left| iz+\sqrt{2}-i \right|=1\), tìm ra đường biểu diễn \(\left( C \right)\) của các số phức z. +) Gọi A, B lần lượt là điểm biểu diễn của \({{z}_{1}};{{z}_{2}}\Rightarrow \left| {{z}_{1}}-{{z}_{2}} \right|=AB\Rightarrow \) vị trí của AB đối với đường tròn \(\left( C \right)\) \(\Rightarrow \left| {{z}_{1}} \right|+\left| {{z}_{2}} \right|=OA+OB\) +) Sử dụng công thức trung tuyến tính \(O{{A}^{2}}+O{{B}^{2}}\) +) Sử dụng BĐT Bunhiascopky tìm GTLN của \(OA+OB\) Lời giải chi tiết: Ta có: \(\left| iz+\sqrt{2}-i \right|=1\Leftrightarrow \left| i\left( x+yi \right)+\sqrt{2}-i \right|=1\) (với \(z=x+yi\ \left( x;y\in R \right)\)) \(\Leftrightarrow {{\left( x-1 \right)}^{2}}+{{\left( y-\sqrt{2} \right)}^{2}}=1\Rightarrow M\left( x;y \right)\) biểu diễn \(z\) thuộc đường tròn tâm \(I\left( 1;\sqrt{2} \right)\) bán kính \(R=1.\) Giả sử \(A\left( {{z}_{1}} \right);B\left( {{z}_{2}} \right)\) do \(\left| {{z}_{1}}-{{z}_{2}} \right|=2\Rightarrow AB=2=2R\) nên \(AB\) là đường kính của đường tròn \(\left( I;R \right)\) Lại có: \(\left| {{z}_{1}} \right|+\left| {{z}_{2}} \right|=OA+OB\) Mặt khác theo công thức trung tuyến ta có: \(O{{I}^{2}}=\frac{O{{A}^{2}}+O{{B}^{2}}}{2}-\frac{A{{B}^{2}}}{4}\Rightarrow O{{A}^{2}}+O{{B}^{2}}=8.\) Theo BĐT Bunhiascopky ta có:\(2\left( O{{A}^{2}}+O{{B}^{2}} \right)\ge {{\left( OA+OB \right)}^{2}}\Rightarrow OA+OB\le 4.\) Chọn D. Câu hỏi 7 : Cho các số phức \({{z}_{1}}=-\,2+i,\,\,{{z}_{2}}=2+i\) và số phức \(z\) thỏa mãn \({{\left| z-{{z}_{1}} \right|}^{2}}+{{\left| z-{{z}_{2}} \right|}^{2}}=16.\) Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \(\left| z \right|.\) Giá trị biểu thức \({{M}^{2}}-{{m}^{2}}\) bằng
Đáp án: C Phương pháp giải: Đặt \(z=x+yi,\) dựa vào giả thiết và biểu thức P đưa về tìm max – min của biểu thức chứa hai biến, sử dụng lượng giác hóa và bất đẳng thức Bunhiacopxki để tìm max – min Lời giải chi tiết: Đặt \(z=x+yi\,\,\,\,\left( x,\,\,y\in \mathbb{R} \right),\) khi đó \({{\left| z-{{z}_{1}} \right|}^{2}}+{{\left| z-{{z}_{2}} \right|}^{2}}=16\Leftrightarrow {{\left( x+2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}+{{\left( x-2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=16\) \(\Leftrightarrow 2{{x}^{2}}+4+2{{y}^{2}}-4y+2=16\Leftrightarrow {{x}^{2}}+{{y}^{2}}-2y-3=0\Leftrightarrow {{x}^{2}}+{{\left( y-1 \right)}^{2}}=4\Leftrightarrow \left\{ \begin{align} x=2\sin t \\ y=2\cos t+1 \\ \end{align} \right..\) Khi đó \({{\left| z \right|}^{2}}={{x}^{2}}+{{y}^{2}}=4{{\sin }^{2}}t+{{\left( 2\cos t+1 \right)}^{2}}=4\cos t+5\) mà \(\cos t\in \left[ -\,1;1 \right]\)\(\Rightarrow \,\,4\cos t+5\in \left[ 1;9 \right].\) Vậy \(1\le \left| z \right|\le 3\,\,\xrightarrow{{}}\,\,\left\{ \begin{align} M=3 \\ m=1 \\ \end{align} \right.\Rightarrow {{M}^{2}}-{{m}^{2}}=8.\) Chọn C Câu hỏi 8 : Cho \(i\) là đơn vị ảo. Gọi \(S\) là tập hợp các số nguyên dương \(n\) có 2 chữ số thỏa mãn \({{i}^{n}}\) là số nguyên dương. Số phần tử của \(S\) là
Đáp án: A Phương pháp giải: Để \({{i}^{n}}\) là số nguyên dương thì \(n\) là số nguyên dương chia hết cho 4 Lời giải chi tiết: Xét \(n=2k,\) khi đó \({{i}^{n}}={{i}^{2k}}={{\left( {{i}^{2}} \right)}^{k}}={{\left( -\,1 \right)}^{k}}\) là số nguyên dương khi \(k\) chẵn. Kết hợp với \(n\in \left\{ 10;\,\,11;\,\,...;\,\,99 \right\}\) suy ra \(\frac{k}{2}\in \left\{ 5;\,\,\frac{11}{2};\,\,...;\,\,\frac{99}{2} \right\}\) và \(k\in \mathbb{Z},\) \(k\) là số chẵn. Với mỗi bộ số \(\left\{ 5;\,\,\frac{11}{2};\,\,...;\,\,\frac{19}{2} \right\}\,\,\xrightarrow{{}}\) có 2 số \(k\) thỏa mãn, \(\left\{ 10;\,\,\frac{21}{2};\,\,...;\,\,\frac{29}{2} \right\}\,\,\xrightarrow{{}}\) có 3 số \(k\) thỏa mãn. Vậy có tất cả \(2.5+3.4=22\) số thỏa mãn yêu cầu bài toán. Chọn A Câu hỏi 9 : Điều kiện cần và đủ để z là một số thực là?
Đáp án: A Phương pháp giải: Lời giải chi tiết: Câu hỏi 10 : Cho hai số phức \({{z}_{1}}=-\,1+2i,\,\,{{z}_{2}}=-\,1-2i.\) Giá trị của biểu thức \({{\left| {{z}_{1}} \right|}^{2}}+{{\left| {{z}_{2}} \right|}^{2}}\) bằng
Đáp án: B Phương pháp giải: Lời giải chi tiết: Câu hỏi 11 : Cho số phức \(z\)thỏa mãn: \(\left| z \right|-2\overline{z}=-7+3i+z\). Tính \(\left| z \right|\).
Đáp án: B Phương pháp giải: +) Gọi số phức đó là \(z=a+bi,\,\,a,b\in R\). Thay vào phương trình, giải tìm a, b. +) Tính \(\left| z \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}\) Lời giải chi tiết: Gọi số phức đó là \(z=a+bi,\,\,a,b\in R\). Khi đó: \(\begin{array}{l}\left| z \right| - 2\overline z = - 7 + 3i + z \Leftrightarrow \sqrt {{a^2} + {b^2}} - 2\left( {a - bi} \right) = - 7 + 3i + a + bi \Leftrightarrow \sqrt {{a^2} + {b^2}} - 2a + 2bi = - 7 + a + \left( {3 + b} \right)i\\ \Leftrightarrow \left\{ \begin{array}{l}\sqrt {{a^2} + {b^2}} - 2a = - 7 + a\\2b = 3 + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\sqrt {{a^2} + {3^2}} - 2a = - 7 + a\\b = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\sqrt {{a^2} + 9} = 3a - 7\\b = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a \ge \frac{7}{3}\\{a^2} + 9 = {\left( {3a - 7} \right)^2}\\b = 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a \ge \frac{7}{3}\\8{a^2} - 42a + 40 = 0\\b = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a \ge \frac{7}{3}\\\left[ \begin{array}{l}a = \frac{5}{4}\\a = 4\end{array} \right.\\b = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 4\\b = 3\end{array} \right. \Rightarrow z = 4 + 3i \Rightarrow \left| z \right| = \sqrt {{4^2} + {3^2}} = 5\end{array}\)
Chọn: B Câu hỏi 12 : Cho số phức \(z\) thỏa mãn \(z - \left| z \right| = - 2 - 4i\). Môđun của z là:
Đáp án: C Phương pháp giải: Chuyển vế, lấy môđun hai vế. Lời giải chi tiết: \(\begin{array}{l}z - \left| z \right| = - 2 - 4i \Leftrightarrow z = \left| z \right| - 2 - 4i \Leftrightarrow {\left| z \right|^2} = {\left( {\left| z \right| - 2} \right)^2} + 16\\ \Leftrightarrow {\left| z \right|^2} = {\left| z \right|^2} - 4\left| z \right| + 4 + 16 \Leftrightarrow 4\left| z \right| = 20 \Leftrightarrow \left| z \right| = 5\end{array}\) Chọn C. Câu hỏi 13 : Cho số phức z thỏa mãn \(z + \left| z \right| = 2 - 8i\). Tìm số phức liên hợp của z
Đáp án: D Phương pháp giải: +) Chuyển vế, để z một vế và chuyển tất cả các số còn lại sang 1 vế. +) Lấy mô đun hai vế, sau đó bình phương, giải phương trình tìm \(\left| z \right|\). +) Thay \(\left| z \right|\) vừa tìm được vào tìm z. Lời giải chi tiết: \(z + \left| z \right| = 2 - 8i \Leftrightarrow z = 2 - \left| z \right| - 8i\) Lấy mô đun hai vế ta có : \(\begin{array}{l}\left| z \right| = \left| {2 - \left| z \right| - 8i} \right|\\ \Leftrightarrow {\left| z \right|^2} = {\left( {2 - \left| z \right|} \right)^2} + {8^2}\\ \Leftrightarrow {\left| z \right|^2} = 4 - 4\left| z \right| + {\left| z \right|^2} + 64\\ \Leftrightarrow 4\left| z \right| = 68\\ \Leftrightarrow \left| z \right| = 17\\ \Rightarrow z + 17 = 2 - 8i \Rightarrow z = - 15 - 8i\end{array}\) Chọn D. Câu hỏi 14 : Tìm hai số thực \(x\) và \(y\) thỏa mãn \(\left( 2x-3yi \right)+\left( 3-i \right)=5x-4i\) với \(i\) là đơn vị ảo.
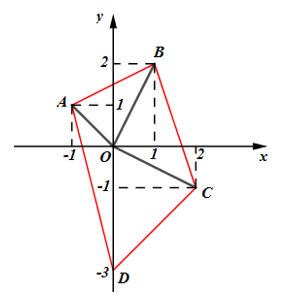
Đáp án: D Phương pháp giải: Hai số phức \({{z}_{1}}={{a}_{1}}+{{b}_{1}}i,\ \ {{z}_{2}}={{a}_{2}}+{{b}_{2}}i\) bằng nhau \(\Leftrightarrow \left\{ \begin{align} & {{a}_{1}}={{a}_{2}} \\ & {{b}_{1}}={{b}_{2}} \\\end{align} \right..\) Lời giải chi tiết: Ta có: \(\ \left( 2x-3yi \right)+\left( 3-i \right)=5x-4i\) \(\begin{array}{l} Chọn D. Câu hỏi 15 : Trong mặt phẳng phức, gọi A, B, C, D lần lượt là các điểm biểu diễn các số phức \({z_1} = - 1 + i,\) \(\,\,{z_2} = 1 + 2i,\,\,{z_3} = 2 - i,\,\,{z_4} = - 3i\). Gọi S diện tích tứ giác ABCD. Tính S.
Đáp án: A Phương pháp giải: +) Tính diện tích các tam giác OAB, OBC, OCD, OAD. +) Sử dụng công thức \({S_{\Delta OAB}} = \frac{1}{2}d\left( {O;AB} \right).AB\) Lời giải chi tiết:
Ta có: \(A\left( { - 1;1} \right);\,\,B\left( {1;2} \right);\,\,C\left( {2; - 1} \right);\,\,D\left( {0; - 3} \right)\). Phương trình AB: \(\frac{{x + 1}}{{1 + 1}} = \frac{{y - 1}}{{2 - 1}} \Leftrightarrow x + 1 = 2y - 2 \Leftrightarrow x - 2y + 3 = 0 \Rightarrow d\left( {O;AB} \right) = \frac{3}{{\sqrt 5 }};\,\,AB = \sqrt 5 \) \( \Rightarrow {S_{\Delta OAB}} = \frac{1}{2}d\left( {O;AB} \right).AB = \frac{1}{2}.\frac{3}{{\sqrt 5 }}.\sqrt 5 = \frac{3}{2}\) Phương trình BC: \(\frac{{x - 1}}{{2 - 1}} = \frac{{y - 2}}{{ - 1 - 2}} \Leftrightarrow - 3x + 3 = y - 2 \Leftrightarrow 3x + y - 5 = 0 \Rightarrow d\left( {O;BC} \right) = \frac{5}{{\sqrt {10} }};\,\,BC = \sqrt {10} \) \( \Rightarrow {S_{\Delta OBC}} = \frac{1}{2}d\left( {O;BC} \right).BC = \frac{1}{2}.\frac{5}{{\sqrt {10} .\sqrt {10} }} = \frac{5}{2}\) Phương trình CD: \(\frac{{x - 2}}{{0 - 2}} = \frac{{y + 1}}{{ - 3 + 1}} \Leftrightarrow - 2x + 4 = - 2y - 2 \Leftrightarrow x - y - 3 = 0 \Rightarrow d\left( {O;CD} \right) = \frac{3}{{\sqrt 2 }};\,\,CD = 2\sqrt 2 \) \( \Rightarrow {S_{\Delta OCD}} = \frac{1}{2}.\frac{3}{{\sqrt 2 }}.2\sqrt 2 = 3\) Phương trình AD: \(\frac{{x + 1}}{{0 + 1}} = \frac{{y - 1}}{{ - 3 - 1}} \Leftrightarrow - 4x - 4 = y - 1 \Leftrightarrow 4x + y + 3 = 0 \Rightarrow d\left( {O;AD} \right) = \frac{3}{{\sqrt {17} }};\,\,AD = \sqrt {17} \) \( \Rightarrow {S_{\Delta OAD}} = \frac{1}{2}.\frac{3}{{\sqrt {17} }}.\sqrt {17} = \frac{3}{2}\) Vậy \(S = {S_{\Delta OAB}} + {S_{\Delta OBC}} + {S_{\Delta OCD}} + {S_{\Delta OAD}} = \frac{{17}}{2}\). Chọn đáp án A. Câu hỏi 16 : Cho số phức \(z = a + bi\,\,\left( {a,b \in \mathbb{R}} \right)\) thỏa mãn \(z + 1 + 3i - \left| z \right|i = 0\). Tính \(S = a - 3b\).
Đáp án: D Phương pháp giải: Đặt \(z = a + bi\), biến đổi VT về dạng \(A + Bi = 0 \Leftrightarrow A = B = 0\), từ đó tìm \(a,b\). Lời giải chi tiết: Ta có: \(z + 1 + 3i - \left| z \right|i = 0 \Leftrightarrow a + bi + 1 + 3i - \sqrt {{a^2} + {b^2}} .i = 0 \Leftrightarrow \left\{ \begin{array}{l}a + 1 = 0\\b + 3 - \sqrt {{a^2} + {b^2}} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b + 3 = \sqrt {1 + {b^2}} \end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b + 3 \ge 0\\{b^2} + 6b + 9 = 1 + {b^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b \ge - 3\\b = - \dfrac{4}{3}\,\,\left( {tm} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b = - \dfrac{4}{3}\end{array} \right.\) \(S = a - 3b = - 1 - 3.\dfrac{{ - 4}}{3} = - 1 + 4 = 3\). Chọn: D Câu hỏi 17 : Cho các số phức \({z_1},\,{z_2}\) thỏa mãn \(\left| {{z_1}} \right| = \left| {{z_2}} \right| = \sqrt 3 \) và \(\left| {{z_1} - {z_2}} \right| = 2.\) Môđun \(\left| {{z_1} + {z_2}} \right|\) bằng
Đáp án: D Phương pháp giải: Modun của số phức \(z = x + yi:\;\;\left| z \right| = \sqrt {{x^2} + {y^2}} .\) Lời giải chi tiết: Gọi số phức \({z_1} = {a_1} + {b_1}i,\,\,{z_2} = {a_2} + {b_2}i \Rightarrow \left\{ \begin{array}{l}{z_1} + {z_2} = {a_1} + {a_2} + \left( {{b_1} + {b_2}} \right)i\\{z_1} - {z_2} = {a_1} - {a_2} + \left( {{b_1} - {b_2}} \right)i\end{array} \right..\) Theo giả thiết ta có: \(\left\{ \begin{array}{l}\left| {{z_1}} \right| = \sqrt 3 \\\left| {{z_2}} \right| = \sqrt 3 \\\left| {{z_1} - {z_2}} \right| = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a_1^2 + b_1^2 = 3\\a_2^2 + b_2^2 = 3\\{\left( {{a_1} - {a_2}} \right)^2} + {\left( {{b_1} - {b_2}} \right)^2} = 4\,\,\,\,\left( 1 \right)\end{array} \right.\) \(\begin{array}{l}\left( 1 \right) \Leftrightarrow a_1^2 + a_2^2 + b_1^2 + b_2^2 - 2{a_1}{a_2} - 2{b_1}{b_2} = 4\\ \Leftrightarrow 6 - 2{a_1}{a_2} - 2{b_1}{b_2} = 4 \Leftrightarrow 2{a_1}{a_2} + 2{b_1}{b_2} = 2\\ \Rightarrow a_1^2 + a_2^2 + b_1^2 + b_2^2 + 2{a_1}{a_2} + 2{b_1}{b_2} = 2 + 6 = 8\\ \Leftrightarrow {\left( {{a_1} + {a_2}} \right)^2} + {\left( {{b_1} + {b_2}} \right)^2} = 8\\ \Leftrightarrow \left| {{z_1} + {z_2}} \right| = \sqrt 8 = 2\sqrt 2 .\end{array}\) Chọn D. Câu hỏi 18 : Cho các số phức \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1}} \right| = 3,\,\left| {{z_2}} \right| = 4\) và \(\left| {{z_1} - {z_2}} \right| = 5\). Gọi A, B lần lượt là điểm biểu diễn các số phức \({z_1},{z_2}\). Diện tích S của tam giác OAB với O là gốc tọa độ là:
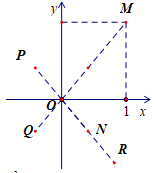
Đáp án: C Phương pháp giải: Sử dụng phương pháp hình học. Lời giải chi tiết: \(\left| {{z_1}} \right| = 3,\,\left| {{z_2}} \right| = 4;\left| {{z_1} - {z_2}} \right| = 5 \Rightarrow OA = 3,\,OB = 4,\,\,AB = 5 \Rightarrow \Delta OAB\) vuông tại O \( \Rightarrow {S_{\Delta OAB}} = \dfrac{1}{2}.OA.OB = \dfrac{1}{2}.3.4 = 6\). Chọn: C Câu hỏi 19 : Trong mặt phẳng phức, cho số phức \(z\) có điểm biểu diễn là \(N.\) Biết rằng số phức \(w = \frac{1}{z}\) được biểu diễn bởi một trong bốn điểm \(M,P,Q,R\) như hình vẽ bên. Hỏi điểm biểu diễn của \(w\) là điểm nào?
Đáp án: D Phương pháp giải: Tính \(\frac{1}{z}\) để tìm được tọa độ điểm biểu diễn số phức \(\frac{1}{z}\) Đánh giá hoành độ và tung độ để xác định xem điểm cần tìm thuộc góc phần tư nào, từ đó chọn đáp án. Lời giải chi tiết: Gọi số phức \(z = a + bi \,\,\left( {a;b \in \mathbb{R}} \right)\) thì điểm \(N\left( {a;b} \right)\) Khi đó số phức \(\frac{1}{z} = \frac{1}{{a + bi}} = \frac{{a - bi}}{{\left( {a + bi} \right)\left( {a - bi} \right)}} = \frac{{a - bi}}{{{a^2} + {b^2}}} = \frac{a}{{{a^2} + {b^2}}} - \frac{b}{{{a^2} + {b^2}}}.i\) Nên điểm biểu diễn số phức \(\frac{1}{z}\) có tọa độ \(\left( {\frac{a}{{{a^2} + {b^2}}}; - \frac{b}{{{a^2} + {b^2}}}} \right)\) Vì điểm \(N\left( {a;b} \right)\) thuộc góc phần tư thứ \(\left( {IV} \right)\) tức là \(a > 0;b < 0\) suy ra \(\frac{a}{{{a^2} + {b^2}}} > 0;\, - \frac{b}{{{a^2} + {b^2}}} > 0\) nên điểm biểu diễn số phức \(\frac{1}{z}\) thuộc góc phần tư thứ \(\left( I \right)\). Từ hình vẽ chỉ có điểm \(M\) thỏa mãn. Chọn D. Câu hỏi 20 : Cho số phức \(z = a + bi\) thỏa mãn \(\left| {z - 1} \right| = \left| {z - i} \right|\) và \(\left| {z - 3i} \right| = \left| {z + i} \right|\). Giá trị của \(a + b\) bằng:
Đáp án: A Phương pháp giải: Sử dụng công thức tính môđun số phức \(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \). Lời giải chi tiết: Theo bài ra ta có: \(\begin{array}{l}\left\{ \begin{array}{l}\left| {a + bi - 1} \right| = \left| {a + bi - i} \right|\\\left| {a + bi - 3i} \right| = \left| {a + bi + i} \right|\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {a - 1} \right)^2} + {b^2} = {a^2} + {\left( {b - 1} \right)^2}\\{a^2} + {\left( {b - 3} \right)^2} = {a^2} + {\left( {b + 1} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 2a + 1 = - 2b + 1\\ - 6a + 9 = 2b + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a - b = 0\\3b + b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 1\end{array} \right. \Rightarrow a + b = 2\end{array}\) Chọn A. Câu hỏi 21 : Trong mặt phẳng tọa độ \(Oxy\), cho điểm \(M,N,P\) lần lượt là điểm biểu diễn của các số phức \(2 + 3i,1 - 2i, - 3 + i\). Tọa độ điểm \(Q\) sao cho tứ giác \(MNPQ\) là hình bình hành là
Đáp án: C Phương pháp giải: - Điểm \(M\left( {a;b} \right)\) biểu diễn số phức \(z = a + bi\). - Tứ giác \(ABCD\) là hình bình hành \( \Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \). Lời giải chi tiết: Ta có: các điểm \(M\left( {2;3} \right),N\left( {1; - 2} \right),P\left( { - 3;1} \right)\) lần lượt biểu diễn các số phức \(2 + 3i,\,\,1 - 2i,\,\, - 3 + i\). Gọi điểm \(Q\left( {x;y} \right)\) thì tứ giác \(MNPQ\) là hình bình hành \( \Leftrightarrow \overrightarrow {MN} = \overrightarrow {QP} \) \( \Leftrightarrow \left\{ \begin{array}{l}1 - 2 = - 3 - x\\ - 2 - 3 = 1 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 2\\y = 6\end{array} \right. \Rightarrow Q\left( { - 2;6} \right)\). Chọn C. Câu hỏi 22 : Số phức \(z\) thỏa mãn \(3 - 2i + \dfrac{{\overline z }}{i}\) là số thực và \(\left| {z + i} \right| = 2\). Phần ảo của \(z\) là:
Đáp án: A Phương pháp giải: Đặt \(z = a + bi\,\,\left( {a,b \in \mathbb{R}} \right) \Rightarrow \overline z = a - bi\). Lời giải chi tiết: Giả sử \(z = a + bi\,\,\left( {a,b \in \mathbb{R}} \right) \Rightarrow \overline z = a - bi\). Theo bài ra ta có: \(3 - 2i + \dfrac{{\overline z }}{i} = 3 - 2i - \left( {a - bi} \right)i = 3 - 2i - ai - b\) là số thực \( \Rightarrow - 2 - a = 0 \Leftrightarrow a = - 2\). \(\begin{array}{l} \Rightarrow z = - 2 + bi \Rightarrow \left| {z + i} \right| = \left| { - 2 + bi + i} \right| = \left| { - 2 + \left( {b + 1} \right)i} \right| = 2\\ \Leftrightarrow \sqrt {4 + {{\left( {b + 1} \right)}^2}} = 2 \Leftrightarrow 4 + {\left( {b + 1} \right)^2} = 4 \Leftrightarrow b + 1 = 0 \Leftrightarrow b = - 1\end{array}\) Vậy \({\mathop{\rm Im}\nolimits} z = b = - 1\). Chọn A Câu hỏi 23 : Xét các khẳng định sau i)\({\left| {{z_1} - {z_2}} \right|^2} = {\left( {{z_1} - {z_2}} \right)^2}_{}^{}\forall {z_1},{z_2} \in \mathbb{C}\) ii)\({\left| {{z_1} - {z_2}} \right|^2} = \left( {{z_1} - {z_2}} \right)\overline {\left( {{z_1} - {z_2}} \right)} _{}^{}\forall {z_1},{z_2} \in \mathbb{C}\) iii)\({\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2} = 2{\left| {\frac{{{z_1} + {z_2}}}{2}} \right|^2} + \frac{1}{2}{\left| {{z_1} - {z_2}} \right|^2}\forall {z_1},{z_2} \in \mathbb{C}\) Số khẳng định đúng là
Đáp án: C Phương pháp giải: +) Đặt \({z_1} = {x_1} + {y_1}i,\,\,{z_2} = {x_2} + {y_2}i\,\,\left( {{x_1};{x_2};{y_1};{y_2} \in \mathbb{R}} \right)\). +) Xét từng đáp án và kết luận, sử dụng các công thức \(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} ;\,\,z.\overline z = {\left| z \right|^2}\). Lời giải chi tiết: Đặt \({z_1} = {x_1} + {y_1}i,\,\,{z_2} = {x_2} + {y_2}i\,\,\left( {{x_1};{x_2};{y_1};{y_2} \in \mathbb{R}} \right)\). i) \(\begin{array}{l}{\left| {{z_1} - {z_2}} \right|^2} = {\left| {{x_1} + {y_1}i - {x_2} - {y_2}i} \right|^2} = {\left( {{x_1} - {x_2}} \right)^2} + {\left( {{y_1} - {y_2}} \right)^2}\\{\left( {{z_1} - {z_2}} \right)^2} = {\left( {{x_1} + {y_1}i - {x_2} - {y_2}i} \right)^2} = {\left( {{x_1} - {x_2}} \right)^2} + 2\left( {{x_1} - {x_2}} \right)\left( {{y_1} - {y_2}} \right)i - {\left( {{y_1} - {y_2}} \right)^2}\end{array}\) \( \Rightarrow i)\) sai. ii) đúng theo công thức \(z.\overline z = {\left| z \right|^2}\) với \(z = {z_1} + {z_2}\). iii) \(\begin{array}{l}VP = \frac{{{{\left| {{z_1} + {z_2}} \right|}^2} + {{\left| {{z_1} - {z_2}} \right|}^2}}}{2}\\ = \frac{{{{\left| {{x_1} + {y_1}i + {x_2} + {y_2}i} \right|}^2} + {{\left| {{x_1} + {y_1}i - {x_2} - {y_2}i} \right|}^2}}}{2}\\ = \frac{{{{\left( {{x_1} + {x_2}} \right)}^2} + {{\left( {{y_1} + {y_2}} \right)}^2} + {{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}}}{2}\\ = \frac{{x_1^2 + 2{x_1}{x_2} + x_2^2 + y_1^2 + 2{y_1}{y_2} + y_2^2 + x_1^2 - 2{x_1}{x_2} + x_2^2 + y_1^2 - 2{y_1}{y_2} + y_2^2}}{2}\\ = \frac{{2x_1^2 + 2y_1^2 + 2x_2^2 + 2y_2^2}}{2} = x_1^2 + y_1^2 + x_2^2 + y_2^2\\VT = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2} = x_1^2 + y_1^2 + x_2^2 + y_2^2 = VP\end{array}\) \( \Rightarrow iii)\) đúng. Chọn C. Câu hỏi 24 : Cho số phức \(z = m - 2 + \left( {{m^2} - 1} \right)i,m \in \mathbb{R}\). Gọi \(\left( C \right)\) là tập hợp các điểm biểu diễn số phức z trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi \(\left( C \right)\) và trục hoành bằng
Đáp án: A Phương pháp giải: - Tìm tọa độ điểm \(M\) biểu diễn số phức \(z\). - Tìm hàm số biểu thị mối liên hệ giữa tọa độ diểm \(M\) không phụ thuộc vào \(m\). - Cho hai hàm số \(f\left( x \right);g\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Diện tích hình phẳng giới hạn bởi đồ thị \(y = f\left( x \right),y = g\left( x \right)\) và các đường thẳng \(x = a,x = b\) bằng \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \). Lời giải chi tiết: Ta có điểm biểu diễn của số phức z là \(M\left( {m - 2;{m^2} - 1} \right) \Rightarrow \left\{ \begin{array}{l}x = m - 2\\y = {m^2} - 1\end{array} \right.\) \( \Rightarrow y + 1 = {\left( {x + 2} \right)^2} \Leftrightarrow y = {x^2} + 4x + 3\) \( \Rightarrow \left( C \right):\,\,y = {x^2} + 4x + 3\) là 1 parabol. Hoành độ giao điểm của đồ thị hàm số \(y = {x^2} + 4x + 3\) với trục hoành là: \({x^2} + 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = - 1\end{array} \right.\) Diện tích hình phẳng cần tìm là \(S = \int\limits_{ - 3}^{ - 1} {\left| {{x^2} + 4x + 3} \right|dx} = - \int\limits_{ - 3}^{ - 1} {\left( {{x^2} + 4x + 3} \right)} = \dfrac{4}{3}.\) Chọn A. Câu hỏi 25 : Cho hai số phức \(z = 3 - 4i\) và \(z' = \left( {2 + m} \right) + mi\,\,\,\left( {m \in \mathbb{R}} \right)\) thỏa mãn \(\left| {z'} \right| = \left| {iz} \right|\). Tổng tất cả các giá trị của m bằng
Đáp án: D Phương pháp giải: - Số phức \(z = a + bi\) có môđun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \). - Lập phương trình bậc hai ẩn \(m\), áp dụng định lí Vi-ét: \({m_1} + {m_2} = \dfrac{{ - b}}{a}\). Lời giải chi tiết: Ta có \(z = 3 - 4i\)\( \Rightarrow iz = i\left( {3 - 4i} \right) = 4 + 3i.\) Theo bài ra ta có: \(\begin{array}{l}\,\,\,\,\,\,\,\left| {z'} \right| = \left| {iz} \right|\\ \Leftrightarrow \sqrt {{{\left( {m + 2} \right)}^2} + {m^2}} = \sqrt {{4^2} + {3^2}} \\ \Leftrightarrow {\left( {m + 2} \right)^2} + {m^2} = 25\\ \Leftrightarrow 2{m^2} + 4m - 21 = 0\end{array}\) Áp dụng định lý viet ta có tổng các giá trị của m là \(\dfrac{{ - 4}}{2} = - 2.\) Chọn D. Câu hỏi 26 : Cho các số phức \({z_1} = 3 - 2i,\) \({z_2} = 1 + 4i\) và \({z_3} = - 1 + i\) có biểu diễn hình học trong mặt phẳng tọa độ Oxy lần lượt là các điểm \(A,B,C\). Diện tích tam giác ABC bằng:
Đáp án: D Phương pháp giải: - Suy ra tọa độ của A,B,C : Số phức \(z = a + bi\) được biểu diễn bởi điểm \(M\left( {a;b} \right)\). - Tính độ dài các đoạn thẳng \(AB,\,\,AC,\,\,BC\). Sử dụng công thức tính độ dài đoạn thẳng \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \). - Sử dụng công thức Herong để tính diện tích tam giác: \({S_{\Delta ABC}} = \sqrt {p\left( {p - AB} \right)\left( {p - AC} \right)\left( {p - BC} \right)} \) với \(p\) là nửa chu vi tam giác \(ABC\). Lời giải chi tiết: Ta có \({z_1} = 3 - 2i,\) \({z_2} = 1 + 4i\) và \({z_3} = - 1 + i\) có biểu diễn hình học trong mặt phẳng tọa độ Oxy lần lượt là các điểm \(A,B,C\)nên \(A\left( {3; - 2} \right);\,\,B\left( {1;4} \right);\,\,C\left( { - 1;1} \right).\) Khi đó ta có: .. Gọi \(p\) là nửa chu vi tam giác \(ABC\) ta có: \(p = \dfrac{{2\sqrt {10} + 5 + \sqrt {13} }}{2}.\) Diện tích tam giác \(ABC\) là: \({S_{\Delta ABC}} = \sqrt {p\left( {p - AB} \right)\left( {p - AC} \right)\left( {p - BC} \right)} = 9.\) Chọn D. Câu hỏi 27 : Có bao nhiêu số phức \(z = a + bi\) với \(a,\,\,b\) tự nhiên thuộc đoạn \(\left[ {2;9} \right]\) và tổng \(a + b\) chia hết cho 3?
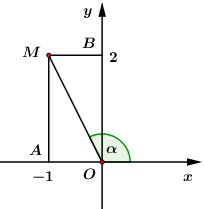
Đáp án: D Phương pháp giải: Áp dụng tính chất chia hết cho 3: Số chia hết cho 3 là số có tổng tất cả các chữ số chia hết cho 3. Lời giải chi tiết: Trong đoạn \(\left[ {2;9} \right]\) có +) 3 số chia hết cho 3: \(\left\{ {3;6;9} \right\}\). +) 2 số chia 3 dư 1: \(\left\{ {4;7} \right\}\). +) 3 số chia 3 dư 2: \(\left\{ {2;5;8} \right\}\). Để \(a + b\) chia hết cho 3 thì +) Cả 2 số a, b đều chia hết cho 3 có \(A_3^2 = 6\) số phức thỏa mãn. +) 1 số chia 3 dư 1 và 1 số chia 3 dư 2: Có \(C_2^1.C_3^1.2! = 12\) số phức thỏa mãn. Vậy có tất cả 18 số phức thỏa mãn. Chọn D. Câu hỏi 28 : Trên mặt phẳng tọa độ \(Oxy,\) gọi \(M\) là điểm biểu diễn hình học của số phức \(z = - 1 + 2i\) và \(\alpha \) là góc lượng giác có tia đầu \(Ox,\) tia cuối \(OM.\) Tính \(\tan 2\alpha .\)
Đáp án: D Phương pháp giải: Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) thì \(M\left( {a;\,\,b} \right)\) là điểm biểu diễn số phức \(z.\) Lời giải chi tiết: Ta có: \(z = - 1 + 2i\) có điểm biểu diễn là \(M\left( { - 1;\,\,2} \right).\)
Ta có: \(\tan AOM = \dfrac{{AM}}{{OA}} = \dfrac{2}{1} = 2.\) \( \Rightarrow \tan \alpha = - \tan AOM = - 2\) (hai góc bù nhau) \( \Rightarrow \tan 2\alpha = \dfrac{{2\tan \alpha }}{{1 - {{\tan }^2}\alpha }} = \dfrac{{2.\left( { - 2} \right)}}{{1 - {{\left( { - 2} \right)}^2}}} = \dfrac{4}{3}\) Chọn D. Câu hỏi 29 : Có bao nhiêu số phức z thoả mãn \(\left| z \right|\left( {z - 6 - i} \right) + 2i = \left( {7 - i} \right)z\)?
Đáp án: B Phương pháp giải: Cô lập z, môđun hai vế. Lời giải chi tiết: \(\begin{array}{l}\left| z \right|\left( {z - 6 - i} \right) + 2i = \left( {7 - i} \right)z\\ \Leftrightarrow \left( {\left| z \right| - 7 + i} \right)z = \left( {6 + i} \right)\left| z \right| - 2i\\ \Leftrightarrow z = \dfrac{{6\left| z \right| + \left( {\left| z \right| - 2} \right)i}}{{\left( {\left| z \right| - 7} \right) + i}}\end{array}\) Lấy môđun hai vế ta có: \(\begin{array}{l}{\left| z \right|^2} = \dfrac{{36{{\left| z \right|}^2} + {{\left( {\left| z \right| - 2} \right)}^2}}}{{{{\left( {\left| z \right| - 7} \right)}^2} + 1}} = \dfrac{{37{{\left| z \right|}^2} - 4\left| z \right| + 4}}{{{{\left| z \right|}^2} - 14\left| z \right| + 50}}\\ \Leftrightarrow {\left| z \right|^4} - 14{\left| z \right|^3} + 50{\left| z \right|^2} = 37{\left| z \right|^2} - 4\left| z \right| + 4\\ \Leftrightarrow {\left| z \right|^4} - 14{\left| z \right|^3} + 13{\left| z \right|^2} + 4\left| z \right| - 4 = 0\\ \Leftrightarrow {\left| z \right|^2}\left( {\left| z \right| - 1} \right)\left( {\left| z \right| - 13} \right) + 4\left( {\left| z \right| - 1} \right) = 0\\ \Leftrightarrow \left( {\left| z \right| - 1} \right)\left( {{{\left| z \right|}^3} - 13{{\left| z \right|}^2} + 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\left| z \right| = 1\\\left| z \right| \approx 12,98\\\left| z \right| \approx 0,58\end{array} \right.\end{array}\) Khi \(\left| z \right| = 1\), thay vào phương trình ban đầu ta có \(\begin{array}{l}z - 6 - i + 2i = \left( {7 - i} \right)z\\ \Leftrightarrow z\left( {1 - 7 + i} \right) = 6 - i\\ \Leftrightarrow z = \dfrac{{6 - i}}{{ - 6 + i}} = - 1\end{array}\) Tương tự với hai giá trị còn lại của \(\left| z \right|\) ta tìm được hai giá trị số phức z tương ứng. Vậy có 3 số phức z thỏa mãn yêu cầu bài toán. Chọn B. Câu hỏi 30 : Cho số phức z thỏa mãn điều kiện \(\left| z \right| = 1\). Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P = \left| {{z^2} + 3z + \overline z } \right| - \left| {z + \overline z } \right|\). Tính \(M + m.\)
Đáp án: D Phương pháp giải: Đặt \(z = a + bi\) rồi tính môđun của P. Rút b theo a rồi tìm giá trị lớn nhất và nhỏ nhất. Lời giải chi tiết: Đặt \(z = a + bi\) \(\left( {a,\,\,b \in \mathbb{R}} \right)\). Theo bài ra ta có: \(\left| z \right| = 1\) \( \Rightarrow {a^2} + {b^2} = 1\)\( \Rightarrow - 1 \le a \le 1\). Khi đó ta có: \(\begin{array}{l}P = \left| {{z^2} + 3z + \overline z } \right| - \left| {z + \overline z } \right|\\P = \left| {{{\left( {a + bi} \right)}^2} + 3\left( {a + bi} \right) + a - bi} \right| - \left| {a + bi + a - bi} \right|\\P = \left| {{a^2} - {b^2} + 4a + 2abi + 2bi} \right| - \left| {2a} \right|\\P = \sqrt {{{\left( {{a^2} - {b^2} + 4a} \right)}^2} + {{\left( {2ab + 2b} \right)}^2}} - \left| {2a} \right|\\P = \sqrt {{{\left( {{a^2} - \left( {1 - {a^2}} \right) + 4a} \right)}^2} + {{\left[ {2b\left( {a + 1} \right)} \right]}^2}} - \left| {2a} \right|\\P = \sqrt {{{\left( {2{a^2} + 4a - 1} \right)}^2} + 4\left( {1 - {a^2}} \right){{\left( {a + 1} \right)}^2}} - \left| {2a} \right|\\P = \sqrt {4{a^4} + 16{a^2} + 1 + 16{a^3} - 4{a^2} - 8a + 4\left( { - {a^4} - 2{a^3} + 2a + 1} \right)} - \sqrt {4{a^2}} \\P = \sqrt {8{a^3} + 12{a^2} + 5} - \sqrt {4{a^2}} \end{array}\) Sử dụng MODE 7 ta tìm được \(M = \max P = 3,\,\,m = \min P = 1\). Vậy\(M + m = 3 + 1 = 4\). Chọn D. Quảng cáo
|