30 bài tập số phức mức độ nhận biếtLàm bàiQuảng cáo
Câu hỏi 1 : Có bao nhiêu số phức z thỏa mãn đồng thời các điều kiện \(|z|=5\) và \(z=\bar{z}\).
Đáp án: B Phương pháp giải: Gọi số phức cần tìm là \(z=a+bi\left( a,b\in R \right)\) , thay vào các hệ thức trong bài và tìm \(a,b\). Lời giải chi tiết: Giả sử số phức cần tìm là \(z=a+bi\). Từ điều kiện \(z=\bar{z}\) ta có \(a+bi=a-bi\Leftrightarrow b=0\) Từ điều kiện \(|z|=5\Rightarrow a=\pm 5\) Chọn B Câu hỏi 2 : Có bao nhiêu số phức thỏa mãn đồng thời các điều kiện \(|z|=4\) và \(z=-\bar{z}\).
Đáp án: B Phương pháp giải: Gọi số phức cần tìm là \(z=a+bi\left( a,b\in R \right)\), thay vào các hệ thức trong bài và tìm \(a,b\)
Lời giải chi tiết: Giả sử số phức cần tìm là \(z=a+bi\). Từ điều kiện \(z=-\bar{z}\) ta có \(a+bi=-(a-bi)\Leftrightarrow a=0\) Từ điều kiện \(|z|=4\Rightarrow b=\pm 4\) Chọn B Câu hỏi 3 : Tìm số điểm biểu diễn cho số phức z thỏa mãn đồng thời các điều kiện: \(|z+4|=3|z|\) và z là thuần ảo?
Đáp án: D Phương pháp giải: Gọi số phức cần tìm là \(z=a+bi\left( a,b\in R \right)\), thay vào các hệ thức trong bài và tìm \(a,b\). Điểm biểu diễn số phức \(z=a+bi\) trên mặt phẳng phức có tọa độ \(\left( a;b \right)\). Lời giải chi tiết: Vì z là thuần ảo nên \(a=0\Rightarrow z=bi\). Từ điều kiện \(|z+4|=3|z|\) có \(\left| bi+4 \right|=3\left| bi \right|\Leftrightarrow{{b}^{2}}+{{4}^{2}}=9{{b}^{2}}\Leftrightarrow 8{{b}^{2}}=16\Leftrightarrow {{b}^{2}}=2\Leftrightarrow b=\pm \sqrt{2}\) Mỗi một số phức z chỉ có 2 điểm biểu diễn trên mặt phẳng phức. Chọn D Câu hỏi 4 : Tìm số điểm biểu diễn cho số phức z thỏa mãn đồng thời các điều kiện: \(|z+2i|=|z+4|\) và phần ảo của z bằng 0?
Đáp án: A Phương pháp giải: Gọi số phức cần tìm là \(z=a+bi\left( a,b\in R \right)\), thay vào các hệ thức trong bài và tìm \(a,b\). Điểm biểu diễn số phức \(z=a+bi\) trên mặt phẳng phức có tọa độ \(\left( a;b \right)\).
Lời giải chi tiết: Vì phần ảo của z bằng 0 nên giả sử \(z=a\), từ điều kiện \(|z+2i|=|z+4|\) có \(|a+2i|=|a+4|\Leftrightarrow {{a}^{2}}+4={{(a+4)}^{2}}\Leftrightarrow 8a+12=0\Leftrightarrow a=-\frac{3}{2}\). Suy ra \(z=-\frac{3}{2}\). Mỗi một số phức z chỉ có 1 điểm biểu diễn trên mặt phẳng phức. Chọn A Câu hỏi 5 : Số phức z thỏa mãn đồng thời các điều kiện \(|z-5|=|z-2-3i|\) và phần thực, phần ảo của z có giá trị đối nhau là
Đáp án: C Phương pháp giải: Gọi số phức cần tìm là \(z=a+bi\left( a,b\in R \right)\), thay vào các hệ thức trong bài và tìm \(a,b\Rightarrow z\). Lời giải chi tiết: Giả sử số phức cần tìm là \(z=a+bi\). Vì phần thực, phần ảo của z có giá trị đối nhau nên \(a+b=0\) .(1) Từ điều kiện \(|z-5|=|z-2-3i|\) có \(|a+bi-5|=|a+bi-2-3i| \) \(\Leftrightarrow {{(a-5)}^{2}}+{{b}^{2}}={{(a-2)}^{2}}+{{(b-3)}^{2}}\) \(\Leftrightarrow -10a+25=-4a+4-6b+9\) \(\Leftrightarrow -6a+6b=-12\Leftrightarrow -a+b=-2\) (2) Giải hệ (1) (2) có \(b=-1,a=1\Rightarrow z=1-i\). Chọn C. Câu hỏi 6 : Có bao nhiêu số phức z thỏa mãn đồng thời các điều kiện: \(|z+6|=5\) và phần ảo của z bằng 4?
Đáp án: D Phương pháp giải: Gọi số phức cần tìm là \(z=a+bi\left( a,b\in R \right)\), thay vào các hệ thức trong bài và tìm \(a,b\Rightarrow z\).
Lời giải chi tiết: Vì z có phần ảo bằng 4 nên \(z=a+4i\). Từ điều kiện \(|z+6|=5\) có \(\begin{array}{l} Phương trình có 2 nghiệm. Suy ra tìm được 2 số phức thỏa mãn. Chọn D Câu hỏi 7 : Cho số phức \(z=5-4i.\) Số phức đối của \(z\) có điểm biểu diễn hình học là
Đáp án: D Phương pháp giải: Số phức \(z=a+bi\) có số phức đối là \(z'=-\,a-bi\) và điểm biểu diễn số phức z’ trong mặt phẳng là : \(M\left( -a;\ -b \right).\) Lời giải chi tiết: Ta có \(z=5-4i\,\,\Rightarrow \,\,\)Số phức đối của \(z\) là \(w=-\,5+4i\) và có điểm biểu diễn hình học là \(\left( -\,5;4 \right).\) Chọn D Câu hỏi 8 : Tìm số phức z thỏa mãn \(\overline z = 2 - i\) là
Đáp án: A Phương pháp giải: Số phức \(z = a + bi\) có số phức liên hợp \(\overline z = a - bi\). Lời giải chi tiết: Ta có \(\overline z = 2 - i \Rightarrow z = 2 + i.\) Chọn A. Câu hỏi 9 : Cho số phức \(z = 3 + 2i\). Giá trị của \(z.\overline z \) bằng
Đáp án: C Phương pháp giải: Sử dụng công thức \(z.\overline z = {\left| z \right|^2}\). Lời giải chi tiết: \(z.\overline z = {\left| z \right|^2} = {3^2} + {2^2} = 13.\) Chọn C. Câu hỏi 10 : Cho hai số phức \({z_1} = - 1 + 2i;\) \({z_2} = 1 + 2i\). Tinh \(T = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2}\)
Đáp án: C Phương pháp giải: Số phức \(z = a + bi\) có môđun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \). Lời giải chi tiết: Ta có \(\begin{array}{l}{z_1} = - 1 + 2i \Rightarrow \left| {{z_1}} \right| = \sqrt {{{\left( { - 1} \right)}^2} + {2^2}} = \sqrt 5 \\{z_2} = 1 + 2i \Rightarrow \left| {{z_2}} \right| = \sqrt {{1^2} + {2^2}} = \sqrt 5 \end{array}\) Vậy \(T = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2} = 5 + 5 = 10.\) Chọn C. Câu hỏi 11 : Số phức \(z = 8 - 7i\) có phần thực và phần ảo lần lượt bằng
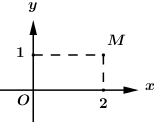
Đáp án: D Phương pháp giải: Số phức \(z = a + bi\) có phần thực là a và phần ảo là b. Lời giải chi tiết: Số phức \(z = 8 - 7i\) có phần thực là 8 và phần ảo là \( - 7\). Chọn D. Câu hỏi 12 : Điểm M trong hình bên là điểm biểu diễn hình học của số phức nào dưới đây?
Đáp án: B Phương pháp giải: Điểm \(M\left( {a;b} \right)\) là điểm biểu diễn hình học của số phức \(z = a + bi\). Lời giải chi tiết: Ta thấy \(M\left( {2;1} \right)\) nên nó biểu diễn cho số phức \(z = 2 + i\). Chọn B. Câu hỏi 13 : Điểm biểu diễn số phức \(z = 1 - 2i\) có tọa độ là:
Đáp án: B Phương pháp giải: Điểm biểu diễn số phức \(z = a + bi\) có tọa độ là: \(M\left( {a;b} \right)\). Lời giải chi tiết: Điểm biểu diễn số phức \(z = 1 - 2i\) có tọa độ là: \(\left( {1; - 2} \right).\) Chọn B. Câu hỏi 14 : Cho số phức \(z = 2 - 5i.\) Phần thực và phần ảo của số phức liên hợp \(\bar z\) là
Đáp án: A Phương pháp giải: - Số phức \(z = a + bi\) có số phức liên hợp \(\bar z = a - bi\). - Số phức \(z = a + bi\) có phần thực bằng \(a\), phần ảo bằng \(b\). Lời giải chi tiết: \(z = 2 - 5i \Rightarrow \bar z = 2 + 5i\). Vậy số phức \(\bar z\) có phần thực bằng 2, phần ảo bằng \(5.\) Chọn A. Câu hỏi 15 : Cho số phức \(z = 1 + 2i.\)Tìm môđun của số phức \(\overline z .\)
Đáp án: A Phương pháp giải: Số phức \(z = x + yi\,\,\left( {x,y \in \mathbb{R}} \right)\) có số phức liên hợp \(\overline z = x - yi\) và \(\left| z \right| = \left| {\overline z } \right| = \sqrt {{x^2} + {y^2}} \). Lời giải chi tiết: \(z = 1 + 2i \Rightarrow \)\(\left| z \right| = \left| {\overline z } \right| = \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \). Chọn A. Câu hỏi 16 : Cho số phức \(z = 4 - 3i.\) Khi đó \(\left| z \right|\) bằng:
Đáp án: B Phương pháp giải: Modun của số phức \(z = x + yi\,\,\,\left( {x,\,\,y \in \mathbb{R}} \right)\) là: \(\left| z \right| = \sqrt {{x^2} + {y^2}} .\) Lời giải chi tiết: Ta có: \(z = 4 - 3i\) \( \Rightarrow \left| z \right| = \sqrt {{4^2} + {{\left( { - 3} \right)}^2}} = 5.\) Chọn B. Câu hỏi 17 : Số phức nào sau đây có biểu diễn hình học là điểm \(M\left( {3; - 5} \right).\)
Đáp án: A Phương pháp giải: Cho số phức \(z = x + yi\;\;\left( {x,\;y \in \mathbb{R}} \right) \Rightarrow M\left( {x;\;y} \right)\) là điểm biểu diễn số phức \(z.\) Lời giải chi tiết: Điểm \(M\left( {3; - 5} \right)\) là điểm biểu diễn hình học của số phức \(z = 3 - 5i.\) Chọn A. Câu hỏi 18 : Modun của số phức \(z = \sqrt 3 - i\) bằng:
Đáp án: D Phương pháp giải: Modun của số phức \(z = x + yi\,\,\,\left( {x,\,\,y \in \mathbb{R}} \right)\) là: \(\left| z \right| = \sqrt {{x^2} + {y^2}} .\) Lời giải chi tiết: Ta có: \(z = \sqrt 3 - 1\) \( \Rightarrow \left| z \right| = \sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( { - 1} \right)}^2}} = 2.\) Chọn D. Câu hỏi 19 : Phần ảo của số phức \(z = 3 + 2i\) bằng:
Đáp án: B Phương pháp giải: Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) thì \(a\) là phần thực, \(b\) là phần ảo của số phức \(z.\) Lời giải chi tiết: Số phức \(z = 3 + 2i\) có phẩn ảo là \(2.\) Chọn B. Câu hỏi 20 : Trên mặt phẳng tọa độ, điểm biểu diễn số phức \(z = 5 + 8i\) là điểm nào dưới đây?
Đáp án: C Phương pháp giải: Cho số phức \(z = x + yi\;\;\left( {x,\;y \in \mathbb{R}} \right) \Rightarrow M\left( {x;\;y} \right)\) là điểm biểu diễn số phức \(z.\) Lời giải chi tiết: Điểm biểu diễn số phức \(z = 5 + 8i\) là: \(P\left( {5;\,\,8} \right).\) Chọn C. Câu hỏi 21 : Số phức liên hợp của \(z = 5 + 4i\) là:
Đáp án: C Phương pháp giải: Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right) \Rightarrow \overline z = a - bi.\) Lời giải chi tiết: Số phức liên hợp của số phức \(z = 5 + 4i\) là: \(\overline z = 5 - 4i.\) Chọn C. Câu hỏi 22 : Cho số phức \(z = 3 - 4i\) Modun của \(z\) bằng
Đáp án: D Phương pháp giải: Modun của số phức \(z = x + yi\,\,\,\left( {x,\,\,y \in \mathbb{R}} \right)\) là: \(\left| z \right| = \sqrt {{x^2} + {y^2}} .\) Lời giải chi tiết: Modun của số phức \(z = 3 - 4i\) là: \(\left| z \right| = \sqrt {{3^2} + {{\left( { - 4} \right)}^2}} = 5.\) Chọn D. Câu hỏi 23 : Phần ảo của số phức \(z = 4 - 5i\) là:
Đáp án: C Phương pháp giải: Số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) có phần thực là \(a\) và phần ảo là \(b.\) Lời giải chi tiết: Số phức \(z = 4 - 5i\) có phần thực là \(4\) và phần ảo là \( - 5.\) Chọn C. Câu hỏi 24 : Cho số phức \(z = 2 + 3i.\) Phần ảo của số phức \(\overline z \) là:
Đáp án: B Phương pháp giải: Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right) \Rightarrow \overline z = a - bi.\) Số phức \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) có phần thực là \(a,\) phần ảo là \(b.\) Lời giải chi tiết: Ta có:\(z = 2 + 3i\) \( \Rightarrow \overline z = 2 - 3i\) \( \Rightarrow \overline z \) có phần ảo là \( - 3.\) Chọn B. Câu hỏi 25 : Cho số phức \(z = 2 + 3i\) có điểm biểu diễn trên mặt phẳng tọa độ là:
Đáp án: B Phương pháp giải: Cho số phức \(z = x + yi\;\;\left( {x,\;y \in \mathbb{R}} \right) \Rightarrow M\left( {x;\;y} \right)\) là điểm biểu diễn số phức \(z.\) Lời giải chi tiết: Điểm biểu diễn của số phức \(z = 2 + 3i\) là: \(\left( {2;\,\,3} \right).\) Chọn B. Câu hỏi 26 : Số phức liên hợp của số phức \(z = 2 - 5i\) là:
Đáp án: D Phương pháp giải: Số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) có số phức liên hợp là:\(\overline z = a - bi.\) Lời giải chi tiết: Số phức liên hợp của số phức \(z = 2 - 5i\) là: \(\overline z = 2 + 5i.\) Chọn D. Câu hỏi 27 : Số phức \(z = 4 - 3i\) có phần ảo bằng:
Đáp án: B Phương pháp giải: Số phức \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) có phần thực là \(a\) và phần ảo là \(b.\) Lời giải chi tiết: Ta có: \(z = 4 - 3i\) có phần thực là \(4\) và phần ảo là \( - 3.\) Chọn B. Câu hỏi 28 : Số phức liên hợp của \(z = 3 + 2i\) là:
Đáp án: B Phương pháp giải: Cho số phức \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right),\) ta có số phức liên hợp của số phức \(z\) là:\(\overline z = a - bi.\) Lời giải chi tiết: Ta có:\(z = 3 + 2i \Rightarrow \overline z = 3 - 2i.\) Chọn B. Câu hỏi 29 : Điểm \(M\left( {3; - 1} \right)\) là điểm biểu diễn của số phức nào sau đây?
Đáp án: C Phương pháp giải: Điểm \(M\left( {x;\,\,y} \right)\) là điểm biểu diễn số phức \(z = x + yi.\) Lời giải chi tiết: Ta có: Điểm \(M\left( {3; - 1} \right)\) là điểm biểu diễn số phức \(z = 3 - i.\) Chọn C. Câu hỏi 30 : Môđun của số phức \(z = - 2 - i\) bằng:
Đáp án: D Phương pháp giải: Áp dụng công thức tính môđun số phức: \(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \). Lời giải chi tiết: \(z = 2 - i \Rightarrow \left| z \right| = \sqrt {{2^2} + {{\left( { - 1} \right)}^2}} = \sqrt 5 \). Chọn D. Quảng cáo
|