25 bài tập ứng dụng tích phân trong hình học mức độ thông hiểuLàm bàiQuảng cáo
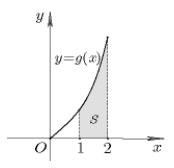
Câu hỏi 1 : Cho hàm số \(y = f\left( x \right)\) liên tục trên R và hàm số \(y = g\left( x \right) = x.f\left( {{x^2}} \right)\) có đồ thị trên đoạn \(\left[ {0;2} \right]\) như hình vẽ bên. Biết diện tích miền được tô màu là \(S = {5 \over 8},\) tính tích phân \(I = \int\limits_1^4 {f\left( x \right){\rm{d}}x} .\)
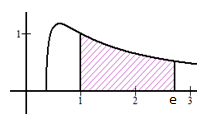
Đáp án: A Phương pháp giải: Dựa vào hình vẽ suy ra diện tích hình phẳng tô đậm theo g(x). Sử dụng phương pháp đổi biến để tính tích phân I. Lời giải chi tiết: Dựa vào hình vẽ, ta thấy rằng \(S = \int\limits_1^2 {\left| {g\left( x \right)} \right|{\rm{d}}x} \) vì \(g\left( x \right) \ge 0,\,\,\forall x \in \left[ {1;2} \right] \Rightarrow S = \int\limits_1^2 {g\left( x \right){\rm{d}}x} = {5 \over 8}\) Khi đó \(S = \int\limits_1^2 {x.f\left( {{x^2}} \right){\rm{d}}x} .\) Đặt \(t = {x^2} \Leftrightarrow {\rm{d}}t = 2x\,{\rm{d}}x \Leftrightarrow x\,{\rm{d}}x = {{{\rm{d}}t} \over 2}\) và đổi cận \(\left\{ \matrix{ x = 1\,\, \Rightarrow \,\,t = 1 \hfill \cr x = 2\,\, \Rightarrow \,\,t = 4 \hfill \cr} \right..\) Vậy \(S = {5 \over 8} \Leftrightarrow \int\limits_1^4 {{1 \over 2}.f\left( t \right){\rm{d}}t} = {5 \over 8} \Leftrightarrow {1 \over 2}.\int\limits_1^4 {f\left( t \right){\rm{d}}t} = {5 \over 8} \Leftrightarrow \int\limits_1^4 {f\left( x \right){\rm{d}}x} = {5 \over 4}\,\,\buildrel {} \over \longrightarrow \,I = {5 \over 4}.\) Chọn A. Câu hỏi 2 : Diện tích hình phẳng giới hạn bởi \(y = {{\sqrt {1 + \ln x} } \over x}; x = 1; x = e\) và trục hoành là \(S\) được biểu diễn dưới dạng \(S = {{a + 4\sqrt 2 } \over b},\) với \(a,\,\,b \in Q\) Tính tổng \(T = a + 2b.\)
Đáp án: C Phương pháp giải: Áp dụng công thức diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \) Đồng nhất hệ số, tìm a, b và tính tổng. Lời giải chi tiết:
Do \({{\sqrt {1 + \ln x} } \over x} \ge 0;\,\,\forall x \in \left[ {1;\,\,e} \right] \Rightarrow \left| {{{\sqrt {1 + \ln x} } \over x}} \right| = {{\sqrt {1 + \ln x} } \over x}\), suy ra diện tích cần xác định là \(S = \int\limits_1^e {\left| {{{\sqrt {1 + \ln x} } \over x}} \right|{\rm{d}}x} = \int\limits_1^e {{{\sqrt {1 + \ln x} } \over x}{\rm{d}}x} \). Đặt \(t = \sqrt {1 + \ln x} \Rightarrow {t^2} = 1 + \ln x \Rightarrow 2t\,{\rm{d}}t = {{{\rm{d}}x} \over x}.\) Khi \(\left\{ \matrix{ x = e\,\, \Rightarrow \,\,t = \sqrt 2 \hfill \cr x = 1\, \Rightarrow t = 1 \hfill \cr} \right..\) Vậy \(S = \int\limits_1^{\sqrt 2 } {t.2t\,{\rm{d}}t} = \int\limits_1^{\sqrt 2 } {2{t^2}\,{\rm{d}}t} = \left. {{2 \over 3}{t^3}} \right|_1^{\sqrt 2 } = {{4\sqrt 2 - 2} \over 3} = {{a + 4\sqrt 2 } \over b} \Rightarrow \left\{ \matrix{ a = - \,2 \hfill \cr b = 3 \hfill \cr} \right..\) Vậy tổng \(T = a + 2b = - \,2 + 2.3 = 4.\) Chọn C. Câu hỏi 3 : Diện tích hình phẳng giới hạn bởi \(y = x\left( {x + 1} \right)\left( {x - 2} \right); x = - \,2; x = 2\) và trục hoành là \(S = {a \over b},\) với \(a,\,\,b > 0\) và \({a \over b}\) là phân số tối giản. Tính giá trị của biểu thức \(P = a - 5b.\)
Đáp án: D Phương pháp giải: Giải phương trình hoành độ giao điểm, tím các nghiệm thuộc [-2; 2]. Áp dụng công thức diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \) Chia nhỏ tích phân cần tính thành các đoạn mà trên các đoạn đó dấu của f(x) là xác định. Lời giải chi tiết: Phương trình hoành độ giao điểm của \(\left( C \right)\) với \(Ox\) là \(x\left( {x + 1} \right)\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \matrix{ x = - \,1 \hfill \cr x = 0 \hfill \cr x = 2 \hfill \cr} \right..\) Vậy diện tích cần tính là \(\eqalign{ & S = \int\limits_{ - 2}^2 {\left| {x\left( {x + 1} \right)\left( {x - 2} \right)} \right|\,{\rm{d}}x} = \int\limits_{ - 2}^{ - 1} {\left| {x\left( {x + 1} \right)\left( {x - 2} \right)} \right|\,{\rm{d}}x} + \int\limits_{ - 1}^0 {\left| {x\left( {x + 1} \right)\left( {x - 2} \right)} \right|\,{\rm{d}}x} + \int\limits_0^2 {\left| {x\left( {x + 1} \right)\left( {x - 2} \right)} \right|\,{\rm{d}}x} \cr & = \left| {\int\limits_{ - \,2}^{ - \,1} {\left( {{x^3} - {x^2} - 2x} \right){\rm{d}}x} } \right| + \left| {\int\limits_{ - \,1}^0 {\left( {{x^3} - {x^2} - 2x} \right){\rm{d}}x} } \right| + \left| {\int\limits_0^2 {\left( {{x^3} - {x^2} - 2x} \right){\rm{d}}x} } \right| \cr & = \left| {\left. {\left( {{{{x^4}} \over 4} - {{{x^3}} \over 3} - {x^2}} \right)} \right|_{ - 2}^{ - 1}} \right| + \left| {\left. {\left( {{{{x^4}} \over 4} - {{{x^3}} \over 3} - {x^2}} \right)} \right|_{ - 1}^0} \right| + \left| {\left. {\left( {{{{x^4}} \over 4} - {{{x^3}} \over 3} - {x^2}} \right)} \right|_0^2} \right| \cr & = \left| { - {5 \over {12}} - {8 \over 3}} \right| + \left| {0 + {5 \over {12}}} \right| + \left| { - {8 \over 3}} \right| = {{37} \over 6} = {a \over b} \Rightarrow \left\{ \matrix{ a = 37 \hfill \cr b = 6 \hfill \cr} \right. \Rightarrow P = 7. \cr} \) Chọn D. Câu hỏi 4 : Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số \(y = {{\ln x} \over {\sqrt x }},\) trục hoành, đường thẳng \(x = 1\) và đường thẳng \(x = e\) bằng \(ae + b.\) Khi đó \({a^2}\) gần với giá trị nào nhất ?
Đáp án: A Phương pháp giải: Áp dụng công thức diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \) Lời giải chi tiết: Ta có \(S = \int\limits_1^e {\left| {{{\ln x} \over {\sqrt x }}} \right|{\rm{d}}x} = \int\limits_1^e {{{\ln x} \over {\sqrt x }}{\rm{d}}x} .\) (Vì với \(x \in \left[ {1;e} \right] \Rightarrow \ln 1 < \ln x < \ln e \Rightarrow \ln x > 0\)) Đặt \(\eqalign{ & \left\{ \matrix{ u = \ln x \hfill \cr dv = {{dx} \over {\sqrt x }} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ du = {{dx} \over x} \hfill \cr v = 2\sqrt x \hfill \cr} \right. \Rightarrow \int\limits_1^e {{{\ln x} \over {\sqrt x }}{\rm{d}}x} = \left. {\ln x.2\sqrt x } \right|_1^e - 2\int\limits_1^e {{{dx} \over {\sqrt x }}} = \left. {\left( {\ln x.2\sqrt x - 4\sqrt x } \right)} \right|_1^e = - 2\sqrt e + 4 = - {2 \over {\sqrt e }}e + 4 \cr & \int\limits_1^e {{{\ln x} \over {\sqrt x }}{\rm{d}}x} = ae + b \Rightarrow \left\{ \matrix{ a = - {2 \over {\sqrt e }} \hfill \cr b = 4 \hfill \cr} \right. \Rightarrow {a^2} = {4 \over e} \approx 1,4715 \approx \sqrt 2 . \cr} \) Chọn A. Câu hỏi 5 : Thể tích khối tròn xoay sinh ra bởi phép quay xung quanh \(Ox\) của hình giới hạn bởi trục \(Ox\) và parabol \(\left( P \right):y={{x}^{2}}-ax\,\,\,\,\left( a>0 \right)\) bằng \(V=2.\) Khẳng định nào dưới đây đúng ?
Đáp án: C Phương pháp giải: Xét phương trình hoành độ giao điểm của (P) và trục Ox, tìm ra các cận x = a và x = b. Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),x=a,x=b\) quanh trục Ox là: \(V=\pi .\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\text{d}x}.\) Lời giải chi tiết: Phương trình hoành độ giao điểm của \(\left( P \right)\) và \(Ox\) là \({{x}^{2}}-ax=0\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=a \\\end{align} \right..\) Khi đó, thể tích cần xác định cho bởi \(V=\pi \int\limits_{0}^{a}{{{\left( {{x}^{2}}-ax \right)}^{2}}\text{d}x}=\pi \int\limits_{0}^{a}{\left( {{x}^{4}}-2a{{x}^{3}}+{{a}^{2}}{{x}^{2}} \right)\text{d}x}\) \(=\pi \left. \left( \frac{{{x}^{5}}}{5}-\frac{a{{x}^{4}}}{2}+\frac{{{a}^{2}}{{x}^{3}}}{3} \right) \right|_{0}^{a}=\frac{\pi {{a}^{5}}}{30}.\) Mặt khác \(V=2\Rightarrow \frac{\pi {{a}^{5}}}{30}=2\Leftrightarrow a=\sqrt[5]{{\frac{{60}}{\pi }}}\in \left( \frac{3}{2};2 \right).\) Chọn C. Câu hỏi 6 : Cho hình phẳng \(\left( H \right)\) giới hạn bởi các đường \(y=\sqrt{x}\), \(y=-\,x\) và \(x=4.\) Thể tích của khối tròn xoay tạo thành khi quay hình \(\left( H \right)\) quanh trục hoành là \(V=\frac{a\pi }{b},\) với \(a,\,\,b>0\) và \(\frac{a}{b}\) là phân số tối giản. Tính tổng \(T=a+b.\)
Đáp án: A Phương pháp giải: Xét phương trình hoành độ giao điểm. Áp dụng công thức tính thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),x=a,x=b\) quanh trục Ox là: \(V=\pi .\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\text{d}x}.\) Đưa tích phân cần tính về dạng \(V=\frac{a\pi }{b},\) và tìm ra các hệ số a và b, thay vào tính tổng a + b. Lời giải chi tiết: Phương trình hoành độ giao điểm của \(y=\sqrt{x},\,\,y=-\,x\) là \(\sqrt{x}=-\,x\Leftrightarrow x=0.\) Khi đó, thể tích cần tính là \(V=\pi \int\limits_{0}^{4}{\left| {{\left( \sqrt{x} \right)}^{2}}-{{\left( -\,x \right)}^{2}} \right|\text{d}x}=\pi \int\limits_{0}^{4}{\left| x-{{x}^{2}} \right|\text{d}x}\) \(=\pi \int\limits_{1}^{4}{\left| x-{{x}^{2}} \right|\text{d}x}+\pi \int\limits_{0}^{1}{\left| x-{{x}^{2}} \right|\text{d}x}=\pi \int\limits_{1}^{4}{\left( {{x}^{2}}-x \right)\text{d}x}+\pi \int\limits_{0}^{1}{\left( x-{{x}^{2}} \right)\text{d}x}\) \( = \pi \left( {\frac{{{x^3}}}{3} - \frac{{{x^2}}}{2}} \right)\left| \begin{array}{l}^4\\_1\end{array} \right. + \pi \left( {\frac{{{x^2}}}{2} - \frac{{{x^3}}}{3}} \right)\left| \begin{array}{l}^1\\_0\end{array} \right. = \frac{{41\pi }}{3} = \frac{{a\pi }}{b}\,\, \Rightarrow \,\,\left\{ \begin{array}{l}a = 41\\b = 3\end{array} \right..\) Vậy \(T=44.\) Chọn A.
Câu hỏi 7 : Cho hình phẳng \(\left( H \right)\) giới hạn bởi các đường \(y=-\,{{x}^{2}}+2x\) và \(y=0\). Tính thể tích của khối tròn xoay tạo thành khi quay hình \(\left( H \right)\) quanh trục Oy là:
Đáp án: B Phương pháp giải: Rút hàm số theo biến y, \(x=f\left( y \right);x=g\left( y \right)\). Giải phương trình tung độ giao điểm để tìm ra các cận y = a và y = b. Áp dụng công thức tính thể tích khối tròn khi xoay quanh trục Oy của hình phẳng bị giới hạn bởi đồ thị các hàm số \(x=f\left( y \right),x=g\left( y \right),y=a,y=b\) là \(V=\int\limits_{a}^{b}{\left| {{f}^{2}}\left( y \right)-{{g}^{2}}\left( y \right) \right|dy}\). Lời giải chi tiết: Ta có \(y=-\,{{x}^{2}}+2x\Rightarrow {{\left( x-1 \right)}^{2}}=1-y\Rightarrow \left[ \begin{align} & \text{ }x=1-\sqrt{1-y} \\ & \text{ }x=1+\sqrt{1-y} \\ \end{align} \right..\) Xét phương trình tung độ giao điểm \(1-\sqrt{1-y}=1+\sqrt{1-y}\Leftrightarrow \sqrt{1-y}=0\Leftrightarrow y=1\). Khi đó, thể tích cần tính là \(V=\pi \int\limits_{0}^{1}{\left| {{\left( 1+\sqrt{1-y} \right)}^{2}}-{{\left( 1-\sqrt{1-y} \right)}^{2}} \right|\text{d}y}=\left| \pi \int\limits_{0}^{1}{4\sqrt{1-y}\,\text{d}y} \right|\) Đặt \(\sqrt{1-y}=t\Leftrightarrow 1-y={{t}^{2}}\Leftrightarrow dy=-2tdt\) Đổi cận: \(\left\{ \begin{align} & y=0\Leftrightarrow t=1 \\ & y=1\Leftrightarrow t=0 \\ \end{align} \right.\) Khi đó \(V=\left| -\pi \int\limits_{1}^{0}{4t.2tdt} \right|=\left| 8\pi \int\limits_{0}^{1}{{{t}^{2}}dt} \right|=\left| 8\left. \pi \frac{{{t}^{3}}}{3} \right|_{0}^{1} \right|=\frac{8\pi }{3}\) Chọn B.
Câu hỏi 8 : Thể tích của khối tròn xoay tạo nên khi quay quanh trục Ox hình phẳng giới hạn bởi \(\left( C \right):y=\ln x,\) trục Ox và đường thẳng \(x=e\) có dạng \(\pi \left( e-a \right)\). Khi đó a bằng:
Đáp án: A Phương pháp giải: Giải phương trình hoành độ giao điểm để tìm các cận. Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),x=a,x=b\) quanh trục Ox là: \(V=\pi .\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\text{d}x}.\) Lời giải chi tiết: Phương trình hoành độ giao điểm của \(\left( C \right)\) và \(Ox\) là \(\ln x=0\Leftrightarrow x=1.\) Khi đó, thể tích cần tính là \(V=\pi \int\limits_{1}^{e}{{{\ln }^{2}}x\,\text{d}x}=\pi \left( x{{\ln }^{2}}x \right)\left| \begin{align} & ^{e} \\ & _{1} \\\end{align} \right.-\pi \int\limits_{1}^{e}{x\,\text{d}\left( {{\ln }^{2}}x \right)}.\) Đặt \(\left\{ \begin{array}{l}u = {\ln ^2}x\\dv = dx\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}du = 2\frac{{\ln x}}{x}dx\\v = x\end{array} \right. \Rightarrow V = \pi \left[ {\left. {x{{\ln }^2}x} \right|_1^e - 2\int\limits_1^e {\ln xdx} } \right] = \pi \left[ {e - 2\int\limits_1^e {\ln xdx} } \right]\) Đặt \(\left\{ \begin{array}{l}u = \ln x\\dv = dx\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}du = \frac{{dx}}{x}\\v = x\end{array} \right. \Leftrightarrow \int\limits_1^e {\ln xdx} = \left. {x\ln x} \right|_1^e - \int\limits_1^e {dx} = \left. {x\ln x} \right|_1^e - \left. x \right|_1^e = e - e + 1 = 1\) Vậy \(I=\pi \left( e-2 \right)\Rightarrow a=2\) Chọn A. Câu hỏi 9 : Người ta tổ chức thực hành nghiên cứu thí nghiệm bằng cách như sau: Họ tiến hành quan sát một tia lửa điện bắn từ mặt đất bắn lên với vận tốc \(15 m/s\). Hỏi biểu thức vận tốc của tia lửa điện là:
Đáp án: A Phương pháp giải: +) Tia lửa điện của trọng lực hướng xuống nên ta có gia tốc \(a = - 9,8\,\,\left( {m/{s^2}} \right)\) +) Sử dụng công thức \(v\left( t \right) = \int {a\left( t \right)dt} \) +) Sử dụng giả thiết v(0) = 15 để tìm hằng số C. Lời giải chi tiết: Tia lửa điện của trọng lực hướng xuống nên ta có gia tốc \(a = - 9,8\,\,\left( {m/{s^2}} \right)\) Ta có biểu thức vận tốc theo thời gian t là \(v\left( t \right) = \int {a\left( t \right)dt} = \int { - 9,8dt} = - 9,8t + C\) Mà \(v\left( 0 \right) = 15 \Rightarrow C = 15 \Rightarrow v = - 9,8t + 15\) Chọn A. Câu hỏi 10 : Người ta tổ chức thực hành nghiên cứu thí nghiệm bằng cách như sau: Họ tiến hành quan sát một tia lửa điện bắn từ mặt đất bắn lên với vận tốc 15 m/s. Hỏi sau 2,5 giây thì tia lửa điện có chiều cao là bao nhiêu?
Đáp án: D Phương pháp giải: +) Tia lửa điện có trọng lực hướng xuống nên ta có gia tốc \(a = - 9,8\,\,\left( {m/{s^2}} \right)\) +) Sử dụng công thức \(v\left( t \right) = \int {a\left( t \right)dt} \) +) Sử dụng giả thiết v(0) = 15 để tìm hằng số C. +) Sử dụng công thức \(S = \int\limits_{{t_1}}^{{t_2}} {v\left( t \right)dt} \) Lời giải chi tiết: Tia lửa điện có trọng lực hướng xuống nên ta có gia tốc \(a = - 9,8\,\,\left( {m/{s^2}} \right)\) Ta có biểu thức vận tốc theo thời gian t là \(v\left( t \right) = \int {a\left( t \right)dt} = \int { - 9,8dt} = - 9,8t + C\) Mà \(v\left( 0 \right) = 15 \Rightarrow C = 15 \Rightarrow v = - 9,8t + 15\) Vậy sau 2,5 giây thì tia lửa điện có chiều cao là \(S = \int\limits_0^{2,5} {\left( { - 9,8t + 15} \right)dt} = 6,875\,\,\left( m \right)\) Chọn D. Câu hỏi 11 : Một vật chuyển động với gia tốc \(a\left( t \right) = - 20{\left( {1 + 2t} \right)^{ - 2}}\,\,\left( {m/{s^2}} \right)\). Khi t = 0 thì vận tốc của vật là 30 m/s. Tính quãng đường vật đó di chuyển sau 2 giây (làm tròn kết quả đến chữ số hàng đơn vị).
Đáp án: C Phương pháp giải: +) Sử dụng công thức \(v\left( t \right) = \int {a\left( t \right)dt} \) +) Sử dụng giả thiết \(v(0) = 30\) để tìm hằng số C. +) Áp dụng công thức \(S = \int\limits_{{t_1}}^{{t_2}} {v\left( t \right)dt} \) Lời giải chi tiết: Ta có \(v\left( t \right) = \int {a\left( t \right)dt} = \int {\frac{{ - 20}}{{{{\left( {1 + 2t} \right)}^2}}}dt} = - \frac{{20}}{2}\frac{{ - 1}}{{1 + 2t}} + C = \frac{{10}}{{1 + 2t}} + C\) Theo đề bài ta có \(v\left( 0 \right) = 30 \Leftrightarrow \frac{{10}}{{1 + 2.0}} + C = 30 \Leftrightarrow C = 20 \Rightarrow v\left( t \right) = \frac{{10}}{{1 + 2t}} + 20\) Vậy quãng đường vật đi được sau 2 giây là : \(S = \int\limits_0^2 {\left( {\frac{{10}}{{1 + 2t}} + 20} \right)dt} = \left. {\left( {5\ln \left( {1 + 2t} \right) + 20t} \right)} \right|_0^2 = 5\ln 5 + 40 = 48\,\,\left( m \right)\) Chọn C. Câu hỏi 12 : Một vật chuyển động với vận tốc \(10\) (m/s) thì tăng tốc với gia tốc \(a(t) = 3t + t^2\)(m/s2). Tính quãng đường mà vật đi được trong khoảng thời gian \(10s\) kể từ lúc bắt đầu tăng tốc (Tính chính xác đến hàng phần trăm).
Đáp án: C Phương pháp giải: +) Sử dụng công thức \(v\left( t \right) = \int {a\left( t \right)dt} \) +) Sử dụng giả thiết \(v(0) = 10\) để tìm hằng số C. +) Áp dụng công thức \(S = \int\limits_{{t_1}}^{{t_2}} {v\left( t \right)dt} \) Lời giải chi tiết: Vận tốc của vật khi bắt đầu tăng tốc là \(v\left( t \right) = \int {\left( {3t + {t^2}} \right)dt} = \frac{{3{t^2}}}{2} + \frac{{{t^3}}}{3} + C\) Mà \(v\left( 0 \right) = 10 \Rightarrow C = 10 \Rightarrow v\left( t \right) = \frac{{3{t^2}}}{2} + \frac{{{t^3}}}{3} + 10\) Quãng đường mà vật đi được trong khoảng thời gian 10s kể từ thời điểm bắt đầu tăng tốc là \(S\left( t \right) = \int\limits_0^{10} {\left( {\frac{{3{t^2}}}{2} + \frac{{{t^3}}}{3} + 10} \right)dt} = 1433,33\,\,\left( m \right)\) Chọn C. Câu hỏi 13 : Một đám vi trùng tại thời điểm t có số lượng là N(t). Biết rằng \(N'\left( t \right) = \frac{{4000}}{{1 + 0,5t}}\) và lúc đầu đám vi trùng có 250000 con. Hỏi sau 10 ngày số lượng vi trùng là bao nhiêu?
Đáp án: A Phương pháp giải: +) Tính \(N\left( t \right) = \int\limits_{}^{} {N'\left( t \right)dt} \) +) Sử dụng giả thiết \(N(0) = 25000\) đề tìm hằng số C. +) Tính \(N(10)\). Lời giải chi tiết: Số lượng vi trùng tại thời điểm t là \(N\left( t \right) = \int\limits_{}^{} {N'\left( t \right)dt} = \int\limits_{}^{} {\frac{{4000}}{{1 + 0,5t}}dt} = 8000\ln \left( {1 + 0,5t} \right) + C\) Mà \(N\left( 0 \right) = C = 250000 \Rightarrow N\left( t \right) = 8000\ln \left( {1 + 0,5t} \right) + 250000\) Vậy sau 10 ngày số lượng vi trùng là: \(N\left( {10} \right) = 8000\ln \left( {1 + 5} \right) + 250000 = 264334\) Chọn A. Câu hỏi 14 : Trong Vật lí, công được hình thành khi một lực tác động vào một vật và gây ra sự dịch chuyển . Ví dụ như đi xe đạp. Một lực F(x) biến thiên , thay đổi, tác động vào một vật thể làm vật này dịch chuyển từ \(x =a\) đến \(x = b\) thì công sinh ra bởi lực này có thể tính theo công thức \({\rm{W}} = \int\limits_a^b {F(x)} dx\). Với thông tin trên, hãy tính công W sinh ra khi một lực \(F(x) = \sqrt {3x - 2} \) tác động vào một vật thể làm vật này di chuyển từ \(x = 1\) đến \(x = 6\).
Đáp án: D Phương pháp giải: Sử dụng đúng công thức trong đề bài. Lời giải chi tiết: Công W sinh ra khi một lực \(F(x) = \sqrt {3x - 2} \) tác động vào một vật thể làm vật này di chuyển từ x = 1 đến x = 6 là \({\rm{W}} = \int\limits_1^6 {\sqrt {3x - 2} } dx = 14\) Chọn D. Câu hỏi 15 : Thể tích khối tròn xoay thu được khi quay quanh trục \(Ox\) hình phẳng giới hạn bởi đồ thị hàm số \(y=\frac{\sqrt{3x+1}}{x+1},\) trục hoành và đường thẳng \(x=1\) là
Đáp án: B Phương pháp giải: Sử dụng công thức tính thể tích khối tròn xoay và các phương pháp tính tích phân Lời giải chi tiết: Phương trình hoành độ giao điểm của \(\left( C \right)\) và \(Ox\) là \(\frac{\sqrt{3x+1}}{x+1}=0\Leftrightarrow 3x+1=0\Leftrightarrow x=-\frac{1}{3}.\) Suy ra thể tích khối tròn xoay cần tính là \(V=\pi \int\limits_{-\frac{1}{3}}^{1}{{{f}^{2}}\left( x \right)\,\text{d}x}=\pi \int\limits_{-\frac{1}{3}}^{1}{\frac{3x+1}{{{\left( x+1 \right)}^{2}}}\,\text{d}x}\) Xét tích phân \(I=\int\limits_{0}^{1}{\frac{3x+1}{{{\left( x+1 \right)}^{2}}}\,\text{d}x}=\int\limits_{-\frac{1}{3}}^{1}{\frac{3\left( x+1 \right)-2}{{{\left( x+1 \right)}^{2}}}\,\text{d}x}=\int\limits_{-\frac{1}{3}}^{1}{\left[ \frac{3}{x+1}-\frac{2}{{{\left( x+1 \right)}^{2}}} \right]\text{d}x}\) \(=\left. \left( 3\ln \left| x+1 \right|+\frac{2}{x+1} \right) \right|_{-\frac{1}{3}}^{1}=3.\ln 2+1-3.\ln \frac{2}{3}-3=3.\ln 3-2.\) Vậy \(V=\pi \left( 3\ln 3-2 \right).\) Chọn B Câu hỏi 16 : Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y=-\,{{x}^{2}}+2x+1\) và \(y=2{{x}^{2}}-4x+1\) là
Đáp án: A Phương pháp giải: Áp dụng phương pháp tính diện tích hình phẳng của hai đồ thị hàm số \(y=f\left( x \right)\) và \(y=g\left( x \right)\). Lời giải chi tiết: Phương trình hoành độ giao điểm của \(\left( {{P}_{1}} \right)\) và \(\left( {{P}_{2}} \right)\) là \(-\,{{x}^{2}}+2x+1=2{{x}^{2}}-4x+1\Leftrightarrow \left[ \begin{align} x=0 \\ x=2 \\ \end{align} \right..\) Khi đó, diện tích hình phẳng cần tính là \(S=\int\limits_{0}^{2}{\left| -\,{{x}^{2}}+2x+1-2{{x}^{2}}+4x-1 \right|\,\text{d}x}=3\,\int\limits_{0}^{2}{\left| {{x}^{2}}-2x \right|\,\text{d}x}\) \(=3\,\left| \int\limits_{0}^{2}{\left( {{x}^{2}}-2x \right)\,\text{d}x} \right|=3\,\left| \left. \left( \frac{{{x}^{3}}}{3}-{{x}^{2}} \right) \right|_{0}^{2} \right|=3\left| \frac{{{2}^{3}}}{3}-{{2}^{2}} \right|=3.\frac{4}{3}=4.\) Vậy diện tích \(S=4.\) Chọn A Câu hỏi 17 : Tính thể tích V của một vật tròn xoay tạo thành khi quay quanh hình phẳng (H) giới hạn bởi các đường \(y={{x}^{2}};\,\,y=\sqrt{x}\) quanh trục Ox.
Đáp án: C Phương pháp giải: Cho hai hàm số \(y\text{ }=\text{ }f\left( x \right)\)và \(y\text{ }=\text{ }g\left( x \right)\)liên tục trên [a; b]. Khi đó thể tích vật thể tròn xoay giới hạn bởi hai đồ thị số \(y\text{ }=\text{ }f\left( x \right)\), \(y\text{ }=\text{ }g\left( x \right)\)và hai đường thẳng \(x\text{ }=\text{ }a;\text{ }y\text{ }=\text{ }b\)khi quay quanh trục Ox là: \(V=~\pi \int_{a}^{b}{\left| {{f}^{2}}(x)-{{g}^{2}}(x) \right|dx}\) Lời giải chi tiết: Phương trình hoành độ giao điểm của \(y={{x}^{2}};\,\,y=\sqrt{x}\) là: \({{x}^{2}}=\sqrt{x},\,\,\left( x\ge 0 \right)\Leftrightarrow \left[ \begin{align} x=0 \\ x=1 \\ \end{align} \right.\) Thể tích V của một vật tròn xoay tạo thành khi quay quanh hình phẳng (H) giới hạn bởi các đường \(y={{x}^{2}};\,\,y=\sqrt{x}\) quanh trục Ox là: \(V=~\pi \int_{0}^{1}{\left| {{\left( {{x}^{2}} \right)}^{2}}-{{\left( \sqrt{x} \right)}^{2}} \right|dx=}\pi \int_{0}^{1}{\left| {{x}^{4}}-x \right|dx=}-\pi \int_{0}^{1}{({{x}^{4}}-x)dx=}=-\pi \left. \left( \frac{{{x}^{5}}}{5}-\frac{{{x}^{2}}}{2} \right)\,\, \right|_{o}^{1}=\frac{3\pi }{10}\) Chọn: C Câu hỏi 18 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^2}\) và đường thẳng \(y = 2x\) là:
Đáp án: C Phương pháp giải: Xét phương trình hoành độ giao điểm \(f\left( x \right) = g\left( x \right)\), suy ra các nghiệm \(x = a;x = b\) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \). Lời giải chi tiết: Xét phương trình hoành độ giao điểm: \({x^2} = 2x \Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = 2 \hfill \cr} \right.\) \( \Rightarrow S = \int\limits_0^2 {\left| {{x^2} - 2x} \right|dx} = \left| {\int\limits_0^2 {\left( {{x^2} - 2x} \right)dx} } \right| = {4 \over 3}\) Chọn C. Câu hỏi 19 : Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = 2{x^2} - 4x - 6\), trục hoành độ và hai đường thẳng \(x = - 2,x = - 4\).
Đáp án: D Phương pháp giải: Phương pháp tìm diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y = f\left( x \right);y = g\left( x \right);x = a;x = b\): Bước 1: Xét phương trình hoành độ giao điểm \(f\left( x \right) = g\left( x \right)\), tìm các nghiệm thuộc \({x_i} \in \left[ {a;b} \right]\,\,\left( {i = 1;2;3;...;n} \right)\) Bước 2: \(\eqalign{ & S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} = \int\limits_a^{{x_1}} {\left| {f\left( x \right) - g\left( x \right)} \right|dx} + \int\limits_{{x_1}}^{{x_2}} {\left| {f\left( x \right) - g\left( x \right)} \right|dx} + ... + \int\limits_{{x_n}}^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \cr & = \left| {\int\limits_a^{{x_1}} {\left( {f\left( x \right) - g\left( x \right)} \right)dx} } \right| + \left| {\int\limits_{{x_1}}^{{x_2}} {\left( {f\left( x \right) - g\left( x \right)} \right)dx} } \right| + ... + \left| {\int\limits_{{x_n}}^b {\left( {f\left( x \right) - g\left( x \right)} \right)dx} } \right| \cr} \) Lời giải chi tiết: Xét phương trình hoành độ giao điểm \(2{x^2} - 4x - 6 = 0 \Leftrightarrow \left[ \matrix{ x = - 1 \notin \left[ { - 4; - 2} \right] \hfill \cr x = 3 \notin \left[ { - 4; - 2} \right] \hfill \cr} \right.\) \( \Rightarrow S = \int\limits_{ - 4}^{ - 2} {\left| {2{x^2} - 4x - 6} \right|dx} = \left| {\int\limits_{ - 4}^{ - 2} {\left( {2{x^2} - 4x - 6} \right)dx} } \right| = {{148} \over 3}\) Chọn D. Câu hỏi 20 : Cho hình phẳng \(D\) giới hạn bởi đường cong \(y = \dfrac{1}{2}{x^2} - x\), trục hoành và các đường thẳng \(x = 1;\,\,x = 4\). Khối tròn xoay tạo thành khi quay \(D\) quanh trục hoành có thể tích bằng:
Đáp án: A Phương pháp giải: - Xét phương trình hoành độ giao điểm, xác định các nghiệm thuộc \(\left[ {0;4} \right]\). - Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\), đường thẳng \(x = a\), \(x = b\) khi quanh quay trục hoành là: \(V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} \). Lời giải chi tiết: Xét phương trình hoành độ giao điểm: \(\dfrac{1}{2}{x^2} - x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \notin \left[ {1;4} \right]\\x = 2 \in \left[ {1;4} \right]\end{array} \right.\). Hình phẳng \(D\) giới hạn bởi đường cong \(y = \dfrac{1}{2}{x^2} - x\), trục hoành và các đường thẳng \(x = 1\), \(x = 4\) có thể tích là: \(V = \pi \int\limits_1^4 {\left| {{{\left( {\dfrac{1}{2}{x^2} - x} \right)}^2}} \right|dx} = \pi \int\limits_1^4 {{{\left( {\dfrac{1}{2}{x^2} - x} \right)}^2}dx} = \dfrac{{42\pi }}{5}\) Chọn A. Câu hỏi 21 : Tính diện tích \(S\) của hình phẳng giới hạn bởi đồ thị các hàm số \(y = {x^2} - 2x\), \(x = 1\), \(x = 4\) và trục hoành.
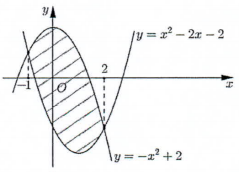
Đáp án: B Phương pháp giải: - Xét phương trình hoành độ giao điểm để tìm các nghiệm thuộc \(\left[ {1;4} \right]\). - Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\), đường thẳng \(x = a,\,\,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \). Lời giải chi tiết: Xét phương trình hoành độ giao điểm: \({x^2} - 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \notin \left[ {1;4} \right]\\x = 2 \in \left[ {1;4} \right]\end{array} \right.\). Hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^2} - 2x\), \(x = 1\), \(x = 4\) và trục hoành có diện tích bằng: \(S = \int\limits_1^4 {\left| {{x^2} - 2x} \right|dx} = \left| {\int\limits_1^2 {\left( {{x^2} - 2x} \right)dx} } \right| + \left| {\int\limits_2^4 {\left( {{x^2} - 2x} \right)dx} } \right|\)\( = \left| { - \dfrac{2}{3}} \right| + \left| {\dfrac{{20}}{3}} \right| = \dfrac{{22}}{3}.\) Chọn B. Câu hỏi 22 : Diện tích phần hình phẳng được gạch chéo trong hình bên bằng
Đáp án: A Phương pháp giải: - Xác định hoành độ giao điểm của 2 đồ thị hàm số dựa vào đồ thị đề bài cho. - Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\), đường thẳng \(x = a,\,\,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) . - Xét dấu biểu thức trong trị tuyệt đối và phá trị tuyệt đối. Lời giải chi tiết: Dựa vào đồ thị hàm số ta thấy nghiệm của phương trình hoành độ giao điểm của 2 đồ thị hàm số là \(\left[ \begin{array}{l}x = - 1\\x = 2\end{array} \right.\). Do đó diện tích phần gạch chéo là: \(S = \int\limits_{ - 1}^2 {\left| { - {x^2} + 2 - {x^2} + 2x + 2} \right|dx} = \int\limits_{ - 1}^2 {\left| { - 2{x^2} + 2x + 4} \right|dx} \). Xét trên \(\left[ { - 1;2} \right]\) ta thấy đồ thị hàm số \(y = - {x^2} + 2\) nằm phía trên đồ thị hàm số \(y = {x^2} - 2x - 2\) nên \( - 2{x^2} + 2x + 4 \ge 0\,\,\forall x \in \left[ { - 1;2} \right]\), do đó \(\left| { - 2{x^2} + 2x + 4} \right| = - 2{x^2} + 2x + 4\) \(\forall x \in \left[ { - 1;2} \right]\). Vậy \(S = \int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx} \). Chọn A. Câu hỏi 23 : Cho hình phẳng \(D\) giới hạn bởi đường cong \(y = \sqrt {2 + \sin x} \), trục hoành và các đường thẳng \(x = 0\), \(x = \pi \). Khối tròn xoay \(D\) tạo thành khi quay \(D\) quanh trục hoành có thể tích \(V\) bằng bao nhiêu?
Đáp án: B Phương pháp giải: Thể tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\), đường thẳng \(x = a\), \(x = b\) là: \(V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} \). Lời giải chi tiết: Xét phương trình hoành độ giao điểm: \(\sqrt {2 + \sin x} = 0 \Leftrightarrow \sin x = - 2\) (vô nghiệm). Khi đó ta có khối tròn xoay \(D\) tạo thành khi quay \(D\) quanh trục hoành có thể tích \(V\) bằng: \(\begin{array}{l}V = \pi \int\limits_0^\pi {\left( {2 + \sin x} \right)dx} = \left. {\pi \left( {2x - \cos x} \right)} \right|_0^\pi \\\,\,\,\, = \pi \left( {2\pi + 1 + 1} \right) = 2\pi \left( {\pi + 1} \right)\end{array}\) Chọn B. Câu hỏi 24 : Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = x{e^x},\)\(\)\(x = 0,\)\(x = 1\) xung quanh trục \(Ox\) là:
Đáp án: A Phương pháp giải: - Xét phương trình hoành độ giao điểm. - Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\), đường thẳng \(x = a\), \(x = b\) khi quanh quay trục hoành là: \(V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} \). Lời giải chi tiết: Xét phương trình hoành độ giao điểm: \(x{e^x} = 0 \Leftrightarrow x = 0\). Hình phẳng giới hạn bởi các đường \(y = x{e^x},\) \(y = 0,\) \(x = 0,\) \(x = 1\) xung quanh trục \(Ox\) là: \(V = \pi \int\limits_0^1 {{{\left( {x{e^x}} \right)}^2}dx} = \pi \int\limits_0^1 {{x^2}{e^{2x}}dx} \) Chọn A. Câu hỏi 25 : Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = {x^2};\)\(x = {y^2}\) xung quanh trục \(Ox\) là:
Đáp án: B Phương pháp giải: - Xét phương trình hoành độ giao điểm. - Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\), đường thẳng \(x = a\), \(x = b\) khi quanh quay trục hoành là: \(V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} \). Lời giải chi tiết: Xét phương trình hoành độ giao điểm: \({x^2} = \pm \sqrt x \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right..\) Thể tích khối tròn xoay là \(V = \pi \int\limits_0^1 {\left| {{x^4} - x} \right|dx} = \dfrac{{3\pi }}{{10}}.\) Chọn B. Quảng cáo
|