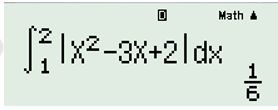25 bài tập ứng dụng tích phân trong hình học mức độ nhận biếtLàm bàiQuảng cáo
Câu hỏi 1 : Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và \(f\left( x \right) < 0;\,\,\forall x \in \left[ {a;b} \right].\) Kí hiệu \(S\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),\) trục hoành và hai đường thẳng \(x = a,\) \(x = b.\) Khẳng định nào dưới đây sai ?
Đáp án: B Phương pháp giải: Diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \), nhận xét dấu của f(x) trên [a; b] và phá trị tuyệt đối. Lời giải chi tiết: Diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \) Mặt khác \(f\left( x \right) < 0;\,\,\forall x \in \left[ {a;b} \right] \Rightarrow S = - \,\int\limits_a^b {f\left( x \right)\,{\rm{d}}x} .\) Chọn B. Câu hỏi 2 : Tích diện tích hình phẳng giới hạn bởi \(x = - \,1;\,\,x = 2;\,\,y = 0;\,\,y = {x^2} - 2x.\)
Đáp án: A Phương pháp giải: Xét phương trình hoành độ giao điểm, tìm các nghiệm thuộc [-1;2]. Diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \), chia đoạn [-1;2] thành các đoạn nhỏ và tính diện tích hình phẳng Lời giải chi tiết: Xét phương trình hoành độ giao điểm \({x^2} - 2x = 0 \Leftrightarrow \left[ \matrix{ x = 0\, \in \left[ { - 1;2} \right] \hfill \cr x = 2 \in \left[ { - 1;2} \right] \hfill \cr} \right.\) Do đó diện tích hình phẳng cần tính là \(S = \int\limits_{ - \,1}^2 {\left| {{x^2} - 2x} \right|{\rm{d}}x} = \int\limits_{ - \,1}^0 {\left| {{x^2} - 2x} \right|{\rm{d}}x} + \int\limits_0^2 {\left| {{x^2} - 2x} \right|{\rm{d}}x} \) \( = \left| {\int\limits_{ - \,1}^0 {\left( {{x^2} - 2x} \right){\rm{d}}x} } \right| + \left| {\int\limits_0^2 {\left( {{x^2} - 2x} \right){\rm{d}}x} } \right| = \left| {\left. {\left( {{{{x^3}} \over 3} - {x^2}} \right)} \right|_{ - \,1}^0} \right| + \left| {\left. {\left( {{{{x^3}} \over 3} - {x^2}} \right)} \right|_0^2} \right| = {4 \over 3} + {4 \over 3} = {8 \over 3}.\) Chọn A. Câu hỏi 3 : Kí hiệu \(S\) là diện tích của hình phẳng giới hạn bởi các đường \(y = x\sin x,\,\,y = 0\) và \(x = 0,\,\,x = \pi .\) Khẳng định nào dưới đây đúng ?
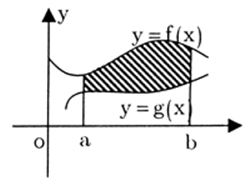
Đáp án: D Phương pháp giải: Xét phương trình hoành độ giao điểm tìm các nghiệm thuộc \(\left[ {0;\pi } \right]\). Áp dụng công thức diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \) Lời giải chi tiết: Xét phương trình hoành độ giao điểm \(x\sin x = 0 \Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr \sin 0 = 0 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ x = 0 \in \left[ {0;\pi } \right] \hfill \cr x = \pi \in \left[ {0;\pi } \right] \hfill \cr} \right.\) Diện tích hình phẳng cần tính là \(S = \int\limits_0^\pi {\left| {x.\sin x} \right|{\rm{d}}x} = \int\limits_0^\pi {x.\sin x\,{\rm{d}}x} \) (\(x \in \left[ {0;\pi } \right] \Rightarrow x\sin x > 0\)). Đặt \(\left\{ \matrix{ u = x \hfill \cr {\rm{d}}v = \sin x\,{\rm{d}}x \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ {\rm{d}}u = {\rm{d}}x \hfill \cr v = - \,\cos x \hfill \cr} \right.\,\, \Rightarrow \,\,S = - \,\left. {x.\cos x} \right|_0^\pi + \int\limits_0^\pi {\cos x\,{\rm{d}}x} = \left. {\left( {\sin x - x.\cos x} \right)} \right|_0^\pi = \pi \) Vậy \(S = \pi \, \Rightarrow \,\,\cos 2S = \cos 2\pi = 1.\) Chọn D. Câu hỏi 4 : Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích khối tròn xoay tạo thành được tính theo công thức nào ?
Đáp án: B Phương pháp giải: Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),y=g\left( x \right),x=a,x=b\) quanh trục Ox là: \(V=\pi .\int\limits_{a}^{b}{\left| {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right|\text{d}x}.\) Lời giải chi tiết: Thể tích khối tròn xoay được tính theo công thức \(V=\pi .\int\limits_{a}^{b}{\left( {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right)\text{d}x}.\) Chọn B.
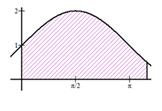
Câu hỏi 5 : Cho hình phẳng \(D\) giới hạn bởi đường cong \(y=\sqrt{2+\sin x},\) trục hoành và các đường thẳng \(x=0,\,\,x=\pi .\) Khối tròn xoay tạo thành khi quay \(D\) quanh trục hoành có thể tích \(V\) bằng bao nhiêu ?
Đáp án: B Phương pháp giải: Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),x=a,x=b\) quanh trục Ox là: \(V=\pi .\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\text{d}x}.\) Lời giải chi tiết: Thể tích khối tròn xoay được tính theo công thức \(V=\pi \int\limits_{0}^{\pi }{{{f}^{2}}\left( x \right)\,\text{d}x}.\) \(=\pi \int\limits_{0}^{\pi }{{{\left( \sqrt{2+\sin x} \right)}^{2}}\,\text{d}x}=\pi \int\limits_{0}^{\pi }{\left( \sin x+2 \right)\,\text{d}x}=\pi \left. \left( 2x-\cos x \right) \right|_{0}^{\pi }=\pi \left( 2\pi +1 \right)+\pi =2\pi \left( \pi +1 \right).\) Chọn B. Câu hỏi 6 : Viết công thức tính thể tích \(V\) của khối tròn xoay được tạo ra khi quay hình thang cong, giới hạn bởi đồ thị hàm số \(y=f\left( x \right),\) trục \(Ox\) và hai đường thẳng \(x = a,\,\,x = b\,\,\left( {a < b} \right)\).
Đáp án: A Phương pháp giải: Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),x=a,x=b\) quanh trục Ox là: \(V=\pi .\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\text{d}x}.\) Lời giải chi tiết: Công thức tính thể tích \(V\) cần tìm là \(V=\pi \,\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\,\text{d}x}.\)
Chọn A. Câu hỏi 7 : Diện tích hình phẳng giới hạn bởi \(y = \sin x + 1; x = 0; x = {{7\pi } \over 6}\) và trục hoành là \(S\) được biển diễn dưới dạng \({{\sqrt 3 } \over a} + {{7\pi } \over b} + c,\) với \(a,\,\,b,\,\,c \in Z.\) Tính tổng \(T = 3a + 2b + c.\)
Đáp án: B Phương pháp giải: Áp dụng công thức diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \) Lời giải chi tiết:
Do \(\sin x + 1 \ge 0;\,\,\forall x \in R\), suy ra diện tích cần tính là: \(S = \int\limits_0^{{{7\pi } \over 6}} {\left| {\sin x + 1} \right|{\rm{d}}x} = \int\limits_0^{{{7\pi } \over 6}} {\left( {\sin x + 1} \right){\rm{d}}x} = \left. {\left( { - \cos x + x} \right)} \right|_0^{{{7\pi } \over 6}} = {{\sqrt 3 } \over 2} + {{7\pi } \over 6} + 1.\) Mặt khác \(S = {{\sqrt 3 } \over a} + {{7\pi } \over b} + c\,\,\left( {a,\,\,b,\,\,c \in Z} \right) \Rightarrow \left\{ \matrix{ a = 2 \hfill \cr b = 6 \hfill \cr c = 1 \hfill \cr} \right. \Rightarrow T = 3.2 + 2.6 + 1 = 19.\) Chọn B. Câu hỏi 8 : Cho hàm số \(y = f\left( x \right)\) liên tục trên R và thỏa mãn \(f\left( { - \,1} \right) > 0 > f\left( 0 \right).\) Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right),\,\,y = 0,\,\,x = - \,1\) và \(x = 1.\) Mệnh đề nào dưới đây là đúng ?
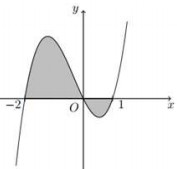
Đáp án: D Phương pháp giải: Diện tích hình phẳng giới hạn bởi \(y = f\left( x \right),\,\,y = 0,\,\,x = a,\,\,x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|{\rm{d}}x} \) Lời giải chi tiết: Diện tích hình phẳng giới hạn bởi \(\left\{ \matrix{ y = f\left( x \right),\,\,y = 0 \hfill \cr x = - \,1,\,\,x = 1 \hfill \cr} \right.\) là \(S = \int\limits_{ - \,1}^1 {\left| {f\left( x \right)} \right|{\rm{d}}x} .\) Chọn D. Câu hỏi 9 : Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Diện tích hình phẳng phần tô đậm trong hình vẽ là
Đáp án: C Phương pháp giải: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), x = a, x = b là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \), lưu ý dấu của f(x) trên mỗi đoạn xác định. Lời giải chi tiết: Dựa vào hình vẽ, ta thấy trên đoạn \(\left\{ \matrix{ x \in \left[ { - \,2;0} \right]\,\, \Rightarrow \,\,f\left( x \right) \ge 0 \hfill \cr x \in \left[ {0;1} \right]\,\, \Rightarrow f\left( x \right) \le 0 \hfill \cr} \right..\) Khi đó \(S = \int\limits_{ - \,2}^1 {\left| {f\left( x \right)} \right|{\rm{d}}x} = \int\limits_{ - \,2}^0 {\left| {f\left( x \right)} \right|{\rm{d}}x} + \int\limits_0^1 {\left| {f\left( x \right)} \right|{\rm{d}}x} = \int\limits_{ - \,2}^0 {f\left( x \right){\rm{d}}x} - \int\limits_0^1 {f\left( x \right){\rm{d}}x} .\) Chọn C. Câu hỏi 10 : Cho hình phẳng giới hạn bởi \(D=\left\{ y=\tan x;\,\,y=0;\,\,x=0;\,\,x=\frac{\pi }{3} \right\}.\) Thể tích vật tròn xoay khi \(D\) quay quanh trục \(Ox\) là \(V=\pi \left( a-\frac{\pi }{b} \right),\) với \(a,\,\,b\in R.\) Tính \(T={{a}^{2}}+2b.\)
Đáp án: B Phương pháp giải: Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),x=a,x=b\) quanh trục Ox là: \(V=\pi .\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\text{d}x}.\) Lời giải chi tiết: Thể tích vật tròn xoay cần tính là \(V=\pi \int\limits_{0}^{\frac{\pi }{3}}{{{\tan }^{2}}x\,\text{d}x}=\pi \int\limits_{0}^{\frac{\pi }{3}}{\left( \frac{1}{{{\cos }^{2}}x}-1 \right)\,\text{d}x}.\) \(=\pi \left. \left( \tan x-x \right) \right|_{0}^{\frac{\pi }{3}}=\pi \left( \sqrt{3}-\frac{\pi }{3} \right)=\pi \left( a-\frac{\pi }{3} \right)\,\,\xrightarrow{{}}\,\,\left\{ \begin{align} & a=\sqrt{3} \\ & b=3 \\\end{align} \right..\) Vậy \(T={{\left( \sqrt{3} \right)}^{2}}+2.3=9.\) Chọn B. Câu hỏi 11 : Bạn Minh ngồi trên máy bay đi du lịch thế giới với vận tốc chuyển động của máy bay là \(v\left( t \right) = 3{t^2} + 5\,\,\left( {m/s} \right)\). Quãng đường máy bay bay từ giây thứ tư đến giây thứ \(10\) là:
Đáp án: D Phương pháp giải: Sử dụng công thức \(S = \int\limits_{{t_1}}^{{t_2}} {v\left( t \right)dt} \) Lời giải chi tiết: Quãng đường máy bay bay từ giây thứ tư đến giây thứ 10 là: \(S = \int\limits_4^{10} {\left( {3{t^2} + 5} \right)dt} = \left. {\left( {{t^3} + 5t} \right)} \right|_4^{10} = 1050 - 84 = 966\,\,\left( m \right)\) Chọn D. Câu hỏi 12 : Một vật chuyển động với vận tốc thay đổi theo thời gian được tính bởi công thức \(v\left( t \right) = 3t + 2\), thời gian tính theo đơn vị giây, quãng đường vật đi được tính theo đơn vị m Biết tại thời điểm \(t = 2s\) thì vật đi được quãng đường là 10m. Hỏi tại thời điểm \(t = 30s\) thì vật đi được quãng đường là bao nhiêu?
Đáp án: A Phương pháp giải: +) Sử dụng công thức \(S = \int\limits_{}^{} {v\left( t \right)dt} \) +) Sử dụng giả thiết \(S\left( 2 \right) = 10\) để tìm hằng số C. +) Tính S(30) Lời giải chi tiết: Quãng đường đi được tại thời gian t là \(S = \int\limits_{}^{} {\left( {3t + 2} \right)dt} = \frac{{3{t^2}}}{2} + 2t + C\) Mà \(S\left( 2 \right) = 10 \Rightarrow 6 + 4 + C = 10 \Rightarrow C = 0 \Rightarrow S\left( t \right) = \frac{{3{t^2}}}{2} + 2t\) Tại thời điểm t = 30s thì vật đi được quãng đường là \(S\left( {30} \right) = \frac{{{{3.30}^2}}}{2} + 2.30 = 1410\,\,\left( m \right)\) Chọn A. Câu hỏi 13 : Một người chạy xe máy chuyển động thẳng theo phương trình \(S\left( t \right) = {t^3} - 3{t^2} + 4t\) trong đó t tính bằng giây (s), S tính bằng mét (m). Gia tốc của xe máy lúc \(t = 2s\) bằng:
Đáp án: B Phương pháp giải: +) Sử dụng các công thức \(v\left( t \right) = \left( {S\left( t \right)} \right)',\,a\left( t \right) = \left( {v\left( t \right)} \right)'\) +) Tính a(2). Lời giải chi tiết: Vận tốc tại thời điểm t là: \(v\left( t \right) = \left( {S\left( t \right)} \right)' = 3{t^2} - 6t + 4\) Gia tốc tại thời điểm t là : \(a\left( t \right) = \left( {v\left( t \right)} \right)' = 6t - 6\) Suy ra gia tốc tại thời điểm t = 2s là \(a\left( 2 \right) = 6.2 - 6 = 6\,\,\left( {m/{s^2}} \right)\) Chọn B. Câu hỏi 14 : Tính thể tích khi \(S=\left\{ y={{x}^{2}}-4x+6;\,\,y=-\,{{x}^{2}}-2x+6 \right\}\) quay quanh trục \(Ox.\)
Đáp án: D Phương pháp giải: Giải phương trình hoành độ giao điểm của 2 đồ thị hàm số tìm ra các cận x = a và x = b. Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường \(y=f\left( x \right),x=a,x=b\) quanh trục Ox là: \(V=\pi .\int\limits_{a}^{b}{{{f}^{2}}\left( x \right)\text{d}x}.\) Lời giải chi tiết: Hoành độ giao điểm của hai parabol là \({{x}^{2}}-4x+6=-\,{{x}^{2}}-2x+6\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=1 \\\end{align} \right..\) Thể tích vật tròn xoay cần tính là \(V=\pi \int\limits_{0}^{1}{\left| {{\left( {{x}^{2}}-4x+6 \right)}^{2}}-{{\left( -\,{{x}^{2}}-2x+6 \right)}^{2}} \right|\text{d}x}\) \(=\pi \int\limits_{0}^{1}{\left( 12{{x}^{3}}-36{{x}^{2}}+24x \right)\text{d}x}=\pi \left. \left( 3{{x}^{4}}-12{{x}^{3}}+12{{x}^{2}} \right) \right|_{0}^{1}=3\pi .\) Chọn D. Câu hỏi 15 : Một vật chuyển động với vận tốc ban đầu 5m/s và có gia tốc được xác định bởi công thức \(a = \frac{2}{{t + 1}}\,\left( {m/{s^2}} \right)\). Vận tốc của vật sau 10s đầu tiên là (Làm tròn kết quả đến hàng đơn vị)
Đáp án: A Phương pháp giải: +) Sử dụng công thức \(v\left( t \right) = \int {a\left( t \right)dt} \) +) Sử dụng giả thiết \(v\left( 0 \right) = 5\) để tìm hằng số C. +) Tính v(10) = ? Lời giải chi tiết: Ta có \(v\left( t \right) = \int {\dfrac{2}{{t + 1}}dt} = 2\ln \left( {t + 1} \right) + C\) Mà vận tốc ban đầu là 5 m/s, tức là \(v\left( 0 \right) = 5 \Leftrightarrow 2\ln \left( {0 + 1} \right) + C = 5 \Leftrightarrow C = 5 \Rightarrow v\left( t \right) = 2\ln \left( {t + 1} \right) + 5\) Vận tốc của vật sau 10s đầu tiên là \(v\left( {10} \right) = 2\ln 11 + 5 \approx 10\,\,\left( {m/s} \right)\) Chọn A. Câu hỏi 16 : Cho hàm số \(y=f\left( x \right)\) liên tục trên đoạn \(\left[ a;\ b \right].\) Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số \(y=f\left( x \right),\) trục hoành và hai đường thẳng \(x=a;\ \ x=b\ \left( a<b \right).\) Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:
Đáp án: D Phương pháp giải: Thể tích của vật tròn xoay giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục Ox và hai đường thẳng \(x=a;\ \ x=b\ \ \left( a<b \right)\) khi quay quanh trục Ox là: \(V=\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x \right)}dx.\) Lời giải chi tiết: Theo lý thuyết, chọn đáp án D. Chọn D. Câu hỏi 17 : Cho hàm số \(y=f\left( x \right)\) liên tục trên đoạn \(\left[ a;b \right]\). Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=a,x=b\left( a<b \right)\). Thể tích của khối của khối tròn xoay tạo thành khi quay \(D\) quanh trục hoành được tính theo công thức:
Đáp án: A Phương pháp giải: Sử dụng công thức tính thể tích khối tròn xoay tạo thành khi quay hình phẳng \(D\) giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và các đường thẳng \(x=a;x=b\) là \(V=\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x \right)dx}\). Lời giải chi tiết: Công thức tính thể tích khối tròn xoay tạo thành là: \(V=\pi \int\limits_{a}^{b}{{{f}^{2}}\left( x \right)dx}\) Chọn A. Câu hỏi 18 : Viết công thức tính thể tích \(V\) của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục Ox và hai đường thẳng \(x = a,x = b\,\,\left( {a < b} \right)\) xung quanh trục \(Ox?\)
Đáp án: B Phương pháp giải: Dựa vào công thức tính thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đồ thị hàm số \(y = f\left( x \right),\,y = g\left( x \right),\,x = a,\,\,x = b\,\,\left( {a < b} \right)\) quanh trục Ox là: \(V = \pi \int\limits_a^b {\left[ {{f^2}\left( x \right) - {g^2}\left( x \right)} \right]} dx\) Lời giải chi tiết: Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đồ thị hàm số \(y = f\left( x \right)\), trục Ox và hai đường thẳng \(x = a,x = b\,\,\left( {a < b} \right)\) xung quanh trục \(Ox\) là: \(V = \pi \int\limits_a^b {{f^2}\left( x \right)} dx\) Chọn B. Câu hỏi 19 : Một vật chuyển động chậm dần đều với vận tốc \(v\left( t \right) = 160 - 10t\,\,\left( {m/s} \right)\). Quãng đường mà vật chuyển động từ thởi điểm t = 0(s) đến thời điểm vật dừng lại là:
Đáp án: B Phương pháp giải: +) Tính thời điểm mà vật dừng lại \(\left( {v\left( t \right) = 0} \right)\). +) Sử dụng công thức \(S = \int\limits_{{t_1}}^{{t_2}} {v\left( t \right)dt} \) Lời giải chi tiết: Khi vật dừng lại ta có \(v\left( t \right) = 160 - 10t = 0 \Rightarrow t = 16\,\,\left( s \right)\) Vậy quãng đường mà vật chuyển động từ thởi điểm t = 0(s) đến thời điểm vật dừng lại là \(S = \int\limits_0^{16} {\left( {160 - 10t} \right)dt} = 1280\,\,\left( m \right)\) Chọn B. Câu hỏi 20 : Tính diện tích S của hình phẳng giới hạn bởi đường thẳng \(y=2x+1\) và đồ thị hàm số \(y={{x}^{2}}-x+3\)
Đáp án: C Phương pháp giải: Xét phương trình hoành độ giao điểm suy ra các nghiệm \(x=a;\,\,x=b\) , khi đó diện tích cần tính là \(S=\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|dx}\) . Lời giải chi tiết: Xét phương trình hoành độ giao điểm:\(2x+1={{x}^{2}}-x+3\Leftrightarrow {{x}^{2}}-3x+2=0\Leftrightarrow \left[ \begin{align} & x=1 \\ & x=2 \\ \end{align} \right.\) \(\Rightarrow S=\int\limits_{1}^{2}{\left| {{x}^{2}}-x+3-2x-1 \right|dx}=\int\limits_{1}^{2}{\left| {{x}^{2}}-3x+2 \right|dx}\), sử dụng MTCT ta có: Vậy \(S=\frac{1}{6}.\) Chọn C. Câu hỏi 21 : Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\left[ a;b \right]\). Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=a,\,\,x=b\,\,\left( a<b \right)\) là:
Đáp án: C Phương pháp giải: Sử dụng công thức ứng dụng tích phân để tính diện tích hình phẳng. Lời giải chi tiết: Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=a,\,\,x=b\,\,\left( a<b \right)\) là \(S=\int\limits_{a}^{b}{\left| f\left( x \right) \right|dx}\). Chọn C. Câu hỏi 22 : Viết công thức tính thể tích \(V\) của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục \(Ox\) tại các điểm \(x = a,\,\,x = b\,\,\,\left( {a < b} \right)\)có thiết diện bị cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\)\(\left( {a \le x \le b} \right)\) là\(S\left( x \right)\).
Đáp án: B Phương pháp giải: Công thức tính thể tích \(m = \dfrac{4}{3}\) của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục \(m = \dfrac{1}{3}\) tại các điểm \(m = 1\) có thiết diện bị cắt bởi mặt phẳng vuông góc với trục \(\ln \left( {{x^2} + 3x + 1} \right) + {x^2} + 3x < 0\) tại điểm có hoành độ \(0\) là\(2\) là : \(V = \int\limits_a^b {S\left( x \right)dx} \). Lời giải chi tiết: Công thức tính thể tích \(m = \dfrac{4}{3}\) của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục \(m = \dfrac{1}{3}\) tại các điểm \(m = 1\) có thiết diện bị cắt bởi mặt phẳng vuông góc với trục \(\ln \left( {{x^2} + 3x + 1} \right) + {x^2} + 3x < 0\) tại điểm có hoành độ \(0\) là\(2\) là : \(V = \int\limits_a^b {S\left( x \right)dx} \). Chọn B. Câu hỏi 23 : Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị các hàm số \(y = f\left( x \right),\)\(y = g\left( x \right)\)và các đường thẳng \(x = a,\,\,x = b\,\,\left( {a < b} \right)\).
Đáp án: A Phương pháp giải: Diện tích hình phẳng được giới hạn bởi đồ thị các hàm số \(y = f\left( x \right),\) \(y = g\left( x \right)\)và các đường thẳng \(x = a,\,\,x = b\,\,\left( {a < b} \right)\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \). Lời giải chi tiết: Diện tích hình phẳng được giới hạn bởi đồ thị các hàm số \(y = f\left( x \right),\) \(y = g\left( x \right)\)và các đường thẳng \(x = a,\,\,x = b\,\,\left( {a < b} \right)\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \). Chọn A. Câu hỏi 24 : Diện tích hình phẳng giới hạn bởi các đường \(y = {x^2} - x\), \(y = 2x - 2\), \(x = 0\), \(x = 3\) được tính bởi công thức:
Đáp án: C Phương pháp giải: Công thức tính diện tích hình phẳng được giới hạn bởi các đường thẳng \(x = a,\;x = b\;\;\left( {a < b} \right)\) và các đồ thị hàm số \(y = f\left( x \right),\;y = g\left( x \right)\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx.} \) Lời giải chi tiết: Diện tích hình phẳng giới hạn bởi các đường \(y = {x^2} - x;\) \(y = 2x - 2;\) \(x = 0;\) \(x = 3\) được tính bởi công thức: \(S = \int\limits_0^3 {\left| {{x^2} - x - \left( {2x - 2} \right)} \right|dx} \) \( = \int\limits_0^3 {\left| {{x^2} - 3x + 2} \right|dx.} \) Chọn C. Câu hỏi 25 : Diện tích \(S\) của hình phẳng giới hạn bởi các đường \(y = - {x^2} + 2x,\,\,y = - 3,\,\,x = 1,\,\,x = 2\) được tính bởi công thức nào dưới đây?
Đáp án: C Phương pháp giải: Công thức tính diện tích hình phẳng được giới hạn bởi các đường thẳng \(x = a,\;x = b\;\;\left( {a < b} \right)\) và các đồ thị hàm số \(y = f\left( x \right),\;y = g\left( x \right)\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx.} \) Lời giải chi tiết: Diện tích \(S\) của hình phẳng giới hạn bởi các đường \(y = - {x^2} + 2x,\,\,y = - 3,\,\,x = 1,\,\,x = 2\) được tính bởi công thức: \(S = \int\limits_1^2 {\left| { - {x^2} + 2x + 3} \right|dx} \) \( = \int\limits_1^2 {\left( { - {x^2} + 2x + 3} \right)dx} \) Chọn C. Quảng cáo
|