25 bài tập hai mặt phẳng song song mức độ nhận biết, thông hiểuLàm bàiQuảng cáo
Câu hỏi 1 : Chọn khẳng định sai trong các khẳng định sau:
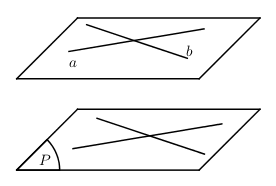
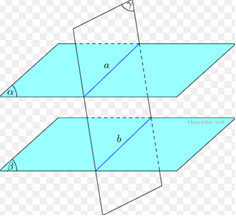
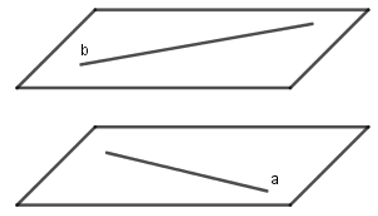
Đáp án: B Phương pháp giải: Suy ra tính đúng sai trực tiếp của từng đáp án. Lời giải chi tiết: A đúng, và tập hợp tất cả các đường thẳng đó tạo thành mặt phẳng qua điểm cho trước và song song với mặt phẳng đã cho. Dễ thấy C và D đúng. Hình trên ta có a và b cùng song song với mặt phẳng (P) tuy nhiên a và b cắt nhau. Đáp án B sai. Câu hỏi 2 : Trong các mệnh đề sau, mệnh đề nào đúng ? - Nếu \(a\subset \,\,mp\,\left( P \right)\) và \(mp\,\left( P \right)\)//\(mp\,\left( Q \right)\) thì \(a\)//\(mp\,\left( Q \right)\) \(\left( I \right).\) - Nếu \(a\subset \,\,mp\,\left( P \right),\,\,b\subset \,\,mp\,\left( Q \right)\) và \(mp\,\left( P \right)\)//\(mp\,\left( Q \right)\) thì \(a\)//\(b\) \(\left( II \right).\) - Nếu \(a\)//\(mp\,\left( P \right),\) \(a\)//\(mp\,\left( Q \right)\) và \(mp\,\left( P \right)\cap mp\,\left( Q \right)=c\) thì \(c\)//\(a\) \(\left( III \right).\)
Đáp án: B Phương pháp giải: Dựa vào lý thuyết quan hệ song song trong không gian Lời giải chi tiết: Dễ thấy \(\left( I I \right)\) sai vì \(a,\,\,b\) có thể chéo nhau, \(\left( I \right)\) và \(\left( I I I \right)\) đúng. Chọn B Câu hỏi 3 : Trong các điều kiện sau, điều kiện nào kết luận \(mp\left( \alpha \right)//mp\left( \beta \right)\)?
Đáp án: D Phương pháp giải: Dựa vào phương pháp chứng minh hai mặt phẳng song song. Lời giải chi tiết: A sai vì \(\left( \alpha \right),\left( \beta \right)\) có thể trùng nhau. B sai vì nếu a // b thì \(\left( \alpha \right),\left( \beta \right)\) chưa chắc song song với nhau. C không thể kết luận được vị trí của \(\left( \alpha \right),\left( \beta \right)\). Chọn D. Câu hỏi 4 : Trong các mệnh đề sau, mệnh đề nào đúng?
Đáp án: A Phương pháp giải: Dựa vào tính chất hai mặt phẳng song song. Lời giải chi tiết: Chọn A. Câu hỏi 5 : Cho hai mặt phẳng song song \(\left( \alpha \right)\) và \(\left( \beta \right)\), đường thẳng \(a//\left( \alpha \right)\). Có mấy vị trí tương đối của a với \(\left( \beta \right)\) ?
Đáp án: B Phương pháp giải: Dựa vào vị trí tương đối giữa đường thẳng và mặt phẳng. Lời giải chi tiết: \(\left\{ \matrix{ \left( \alpha \right)//\left( \beta \right) \hfill \cr a//\left( \alpha \right) \hfill \cr} \right. \Rightarrow \left\{ \matrix{ a \subset \left( \beta \right) \hfill \cr a//\left( \beta \right) \hfill \cr} \right.\) Chọn B. Câu hỏi 6 : Trong các mệnh đề sau, mệnh đề nào đúng?
Đáp án: D Phương pháp giải: Dựa vào định nghĩa và các tính chất hai mặt phẳng song song. Lời giải chi tiết: A và B sai vì nếu \(\left( \alpha \right)//\left( \beta \right)\) và \(a \subset \left( \alpha \right),b \subset \left( \beta \right)\) thì a // b hoặc a và b chéo nhau. C sai vì nếu a // b và \(a \subset \left( \alpha \right),b \subset \left( \beta \right)\) thì \(\left( \alpha \right)//\left( \beta \right)\) hoặc \(\left( \alpha \right) \cap \left( \beta \right) = c//a//b\) D đúng.
Chọn D. Câu hỏi 7 : Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b?
Đáp án: B Phương pháp giải: Lời giải chi tiết:
Có duy nhất một mặt phẳng chứa a và song song với b.
Chọn: B Câu hỏi 8 : Cho lăng trụ \(ABC.A'B'C'\) có tất cả các cạnh bằng nhau. Khi cắt lăng trụ này bởi một mặt phẳng song song với mặt phẳng \(\left( {ABC} \right)\) thì được thiết diện là hình gì?
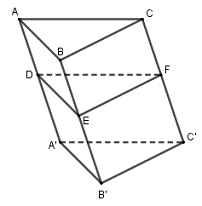
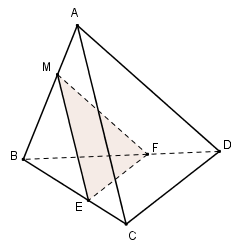
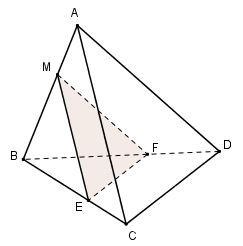
Đáp án: D Phương pháp giải: Dựng hình và nhận xét. Lời giải chi tiết:
Lăng trụ \(ABC.A'B'C'\) có các cạnh bằng nhau nên tam giác \(ABC\) đều. Khi cắt lăng trụ bởi mặt phẳng song song với đáy ta cũng được tam giác đều \(DFE\). Chọn D Câu hỏi 9 : Cho hai mặt phẳng \(\left( \alpha \right);\,\,\left( \beta \right)\) song song với nhau. Xét hai đường thẳng \(a \subset \left( \alpha \right);\)\(b \subset \left( \beta \right)\). Tìm mệnh đề đúng trong các mệnh đề sau ?
Đáp án: B Phương pháp giải: Áp dụng tính chất hai đường thẳng song song trong không gian. Lời giải chi tiết: Ta có \(a \subset \left( \alpha \right);\,\,b \subset \left( \beta \right)\) mà\(\left( \alpha \right)\parallel \left( \beta \right).\) Do đó 2 đường thẳng a,b có thể song song hoặc chéo nhau. Chọn B. Câu hỏi 10 : Cho hình chóp \(S.ABCD\) có đáy là hình thang đáy lớn \(AD\). Gọi \(G\) là trọng tâm tam giác \(SCD\). Thiết diện của hình chóp \(S.ABCD\) khi cắt bởi mp \(\left( {ABG} \right)\) là :
Đáp án: B Phương pháp giải: Sử dụng tính chất song song. Lời giải chi tiết:
Từ \(G\) kẻ đường thẳng song song với \(AB\) lần lượt cắt \(SC,\,\,SD\) tại \(E,\,\,F\). Vậy thiết diện của hình chóp \(S.ABCD\) khi cắt bởi mặt phẳng \(\left( {ABG} \right)\) là hình tứ giác ABEF. Chọn B. Câu hỏi 11 : Tìm mệnh đề đúng trong các mệnh đề sau:
Đáp án: A Phương pháp giải: Lời giải chi tiết: Phương pháp: Nhớ lại các quan hệ song song của đường thẳng mặt phẳng. Cách giải: Đáp án B: \(\left( \alpha \right)//\left( \beta \right),{{d}_{1}}\subset \left( \alpha \right);{{d}_{2}}\subset \left( \beta \right)\) thì \({{d}_{1}}//{{d}_{2}}\) hoặc \({{d}_{1}}\) chéo \({{d}_{2}}\). Loại B. Đáp án C: \({{d}_{1}}\subset \left( \alpha \right);{{d}_{2}}\subset \left( \beta \right);{{d}_{1}}//{{d}_{2}}\) thì có thể xảy ra trường hợp \(\left( \alpha \right)\) cắt \(\left( \beta \right)\) (trong TH này thì \({{d}_{1}}//{{d}_{2}}//\Delta \) với \(\Delta \) là giao tuyến của hai mặt phẳng). Loại C. Đáp án D: Qua một điểm nằm ngoài một mặt phẳng ta vẽ được duy nhất một mặt phẳng song song với mặt phẳng đã cho nên mọi đường thẳng nằm trong mặt phẳng vẽ được sẽ đều song song song với mặt phẳng dã cho. Vậy có vô số đường thẳng \(\Rightarrow \) loại D. Chọn A.
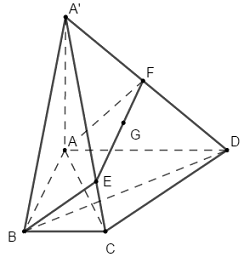
Câu hỏi 12 : Cho tứ diện ABCD có các cạnh bằng a, điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó thiết diện của hình tứ diện cắt bởi mp qua M và song song với mp(ACD) là:
Đáp án: B Phương pháp giải: - Tìm thiết diện dựa vào các yếu tố song song. - Sử dụng định lí Ta-let đảo. - Chứng minh thiết diện là tam giác đều và sử dụng công thức tính diện tích tam giác đều cạnh a là: \(S=\frac{{{a}^{2}}\sqrt{3}}{4}.\) Lời giải chi tiết: Trong (ABC) qua M kẻ đường thẳng song song với AC cắt BC tại E \(\Rightarrow \left( \alpha \right)\cap \left( ABC \right)=ME\). Trong (ABD) qua M kẻ đường thẳng song song với AD cắt BD tại F \(\Rightarrow \left( \alpha \right)\cap \left( ABD \right)=MF.\) \(\Rightarrow \left( \alpha \right)\cap \left( BCD \right)=EF.\) Vậy thiết diện cần tìm là tam giác MEF. Ta có: \(ME\parallel CD\Rightarrow \frac{ME}{CD}=\frac{BM}{AB}\Leftrightarrow \frac{ME}{a}=\frac{a-m}{a}\Leftrightarrow ME=a-m.\) \(\text{EF}\parallel CD\Rightarrow \frac{EF}{CD}=\frac{BE}{BC}=\frac{ME}{AC}\Leftrightarrow \frac{EF}{a}=\frac{a-m}{a}\Rightarrow EF=a-m\) Chứng minh tương tự ta có MF = a – m.. Suy ra tam giác MEF đều cạnh a – m. Vậy \({{S}_{MEF}}=\frac{{{\left( a-m \right)}^{2}}\sqrt{3}}{4}.\) Chọn B.
Câu hỏi 13 : Cho tứ diện đều SABC. Gọi I là trung điểm của AB, M là 1 điểm di động trên đoạn AI. Gọi (P) là mặt phẳng qua M và song song với mp(SIC), biết AM = x. Thiết diện tạo bởi mp(P) và tứu diện SABC có chu vi là:
Đáp án: B Phương pháp giải: - Tìm thiết diện dựa vào các yếu tố song song. - Sử dụng định lí Ta-let đảo. - Tính độ dài các cạnh của tam giác và tính chu vi của tam giác đó. Lời giải chi tiết: Trong (ABC) qua M kẻ đường thẳng song song với CI cắt AC tại N \(\Rightarrow \left( \alpha \right)\cap \left( ABC \right)=MN\). Trong (SAB) qua M kẻ đường thẳng song song với SI cắt SA tại P \(\Rightarrow \left( \alpha \right)\cap \left( SAB \right)=MP.\) \(\Rightarrow \left( \alpha \right)\cap \left( SAC \right)=NP\) và NP // SC. Vậy thiết diện cần tìm là tam giác MNP. Ta có: \(ME\parallel CI \Rightarrow \frac{{MN}}{{CI}} = \frac{{AM}}{{AI}} \Leftrightarrow \frac{{MN}}{{\frac{{AB\sqrt 3 }}{2}}} = \frac{x}{{\frac{{AB}}{2}}} \Leftrightarrow MN = \frac{{\frac{{AB\sqrt 3 }}{2}x}}{{\frac{{AB}}{2}}} = x\sqrt 3 .\) \(\begin{array}{l}MP\parallel SI \Rightarrow \frac{{MP}}{{SI}} = \frac{{AM}}{{AI}} = \frac{{AP}}{{AS}} \Leftrightarrow \frac{{MP}}{{\frac{{AB\sqrt 3 }}{2}}} = \frac{x}{{\frac{{AB}}{2}}} \Rightarrow MP = \frac{{\frac{{AB\sqrt 3 }}{2}x}}{{\frac{{AB}}{2}}} = x\sqrt 3 \\PN\parallel SC \Rightarrow \frac{{AP}}{{AS}} = \frac{{PN}}{{SC}} \Rightarrow \frac{{PN}}{{SC}} = \frac{{AM}}{{AI}} \Leftrightarrow \frac{{PN}}{{SC}} = \frac{x}{{\frac{{AB}}{2}}} \Leftrightarrow PN = \frac{{xSC}}{{\frac{{AB}}{2}}} = 2x\,\,\left( {SC = AB} \right)\end{array}\) Vậy chu vi tam giác MNP là \(2x\sqrt{3}+2x=2x\left( 1+\sqrt{3} \right).\) Chọn B.
Câu hỏi 14 : Cho tứ diện ABCD có các cạnh bằng a, điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó thiết diện của hình tứ diện cắt bởi mp qua M và song song với mp(ACD) là:
Đáp án: B Phương pháp giải: - Tìm thiết diện dựa vào các yếu tố song song. - Sử dụng định lí Ta-let đảo. - Chứng minh thiết diện là tam giác đều và sử dụng công thức tính diện tích tam giác đều cạnh a là: \(S=\frac{{{a}^{2}}\sqrt{3}}{4}.\) Lời giải chi tiết: Trong (ABC) qua M kẻ đường thẳng song song với AC cắt BC tại E \(\Rightarrow \left( \alpha \right)\cap \left( ABC \right)=ME\). Trong (ABD) qua M kẻ đường thẳng song song với AD cắt BD tại F \(\Rightarrow \left( \alpha \right)\cap \left( ABD \right)=MF.\) \(\Rightarrow \left( \alpha \right)\cap \left( BCD \right)=EF.\) Vậy thiết diện cần tìm là tam giác MEF. Ta có: \(ME\parallel CD\Rightarrow \frac{ME}{CD}=\frac{BM}{AB}\Leftrightarrow \frac{ME}{a}=\frac{a-m}{a}\Leftrightarrow ME=a-m.\) \(\text{EF}\parallel CD\Rightarrow \frac{EF}{CD}=\frac{BE}{BC}=\frac{ME}{AC}\Leftrightarrow \frac{EF}{a}=\frac{a-m}{a}\Rightarrow EF=a-m\). Chứng minh tương tự ta có MF = a – m.. Suy ra tam giác MEF đều cạnh a – m. Vậy \({{S}_{MEF}}=\frac{{{\left( a-m \right)}^{2}}\sqrt{3}}{4}.\) Chọn B.
Câu hỏi 15 : Trong các mệnh đề sau, mệnh đề nào đúng:
Đáp án: C Phương pháp giải: Dựa vào định nghĩa các tính chất của hai mặt phẳng song song. Lời giải chi tiết: Đáp án A đúng. Giả sử (P) // (Q), \(a\subset \left( P \right)\Rightarrow a//\left( Q \right)\). Một đường thẳng song song với một mặt phẳng thì a song song với một đường thẳng nào đó nằm trong mặt phẳng (Q). Đáp án B sai: Giả sửa \(\left( \alpha \right)//\left( \beta \right);\,\,a//\left( \beta \right)\Rightarrow \left[ \begin{align} & a\subset \left( \alpha \right) \\ & a//\left( \beta \right) \\ \end{align} \right..\) Đáp án D sai vì hai mặt phẳng phân biệt cùng song song với một đường thẳng chưa chắc song song, chúng có thể cắt nhau theo giao tuyến song song với đường thẳng đó, hoặc trùng nhau. Chọn C.
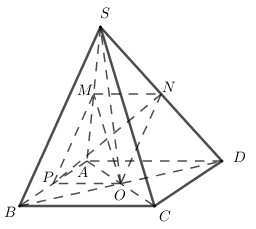
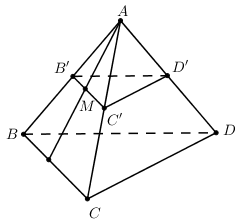
Câu hỏi 16 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P theo thứ tự là trung điểm của SA, SD và AB. Khẳng định nào sau đây đúng?
Đáp án: B Phương pháp giải: \(\left\{ \matrix{ a//\left( \beta \right) \hfill \cr b//\left( \beta \right) \hfill \cr a \cap b \subset \left( \alpha \right) \hfill \cr} \right. \Rightarrow \left( \alpha \right)//\left( \beta \right)\) hoặc \(\left\{ \begin{array}{l}a//a'\\b//b'\\a \cap b \subset \left( \alpha \right)\\a',b' \subset \left( \beta \right)\end{array} \right. \Rightarrow \left( \alpha \right)//\left( \beta \right)\) Lời giải chi tiết:
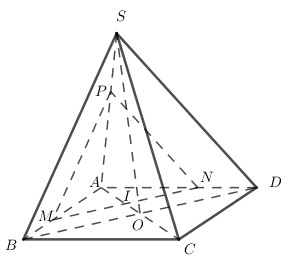
Dễ dàng chứng minh được MNOP là hình bình hành \( \Rightarrow M,N,O,P\) đồng phẳng \( \Rightarrow A,C\) sai. Ta có : MN là đường trung bình của tam giác SAD \( \Rightarrow MN//AD//BC\) ON là đường trung bình của tam giác SBD \( \Rightarrow ON//SB\) \( \Rightarrow \) (MON) // (SBC) \( \Rightarrow \) Đáp án B đúng. Đáp án D sai vì \(N \in \left( {MNP} \right) \cap \left( {SBD} \right)\) Chọn B. Câu hỏi 17 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Tam giác SBD đều. Một mặt phẳng (P) song song với (SBD) và đi qua điểm I thuộc cạnh AC (không trùng với A hoặc C). Thiết diện của (P) với hình chóp là hình gì ?
Đáp án: D Phương pháp giải: Dựng thiết diện bằng cách kẻ các đường thẳng song song. Sử dụng định lí Ta-let. Lời giải chi tiết:
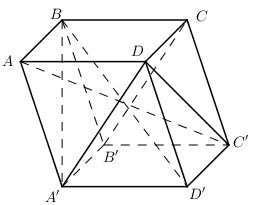
Trong (ABCD) qua I kẻ MN // BD \(\left( {M \in AB;N \in AD} \right)\) Trong (SAB) qua M kẻ MP // SB \(\left( {P \in SA} \right)\) \( \Rightarrow \left( {MNP} \right)//\left( {SBD} \right) \Rightarrow \left( P \right) \equiv \left( {MNP} \right)\) \(\left\{ \matrix{ \left( {MNP} \right) \cap \left( {SAD} \right) = NP \hfill \cr \left( {SBD} \right) \cap \left( {SAD} \right) = SD \hfill \cr \left( {MNP} \right)//\left( {SBD} \right) \hfill \cr} \right. \Rightarrow NP//SD\) Theo định lí Ta-let ta có: \({{MN} \over {BD}} = {{AM} \over {AB}} = {{AP} \over {AS}} = {{MP} \over {SB}} = {{NP} \over {SD}}\) Mà tam giác MNP đều. Chọn D. Câu hỏi 18 : Cho hình hộp ABCD.A’B’C’D’ có các cạnh bên AA’,BB’, CC’, DD’. Khẳng định nào dưới đây là sai?
Đáp án: B Phương pháp giải: Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}AA'//DD'\\AB//CD\end{array} \right.\Rightarrow \left( {AA'B'B} \right)//\left( {DD'C'C} \right) \Rightarrow A\) đúng.
Có: A’B’ // CD và A’B’ = CD nên A’B’CD là hình bình hành, do đó C đúng. D đương nhiên đúng. Chọn B. Câu hỏi 19 : Cho hình lăng trụ ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của BB’và CC’. Gọi \(\Delta \) là giao tuyến của hai mặt phẳng (AMN) và (A’B’C’). Khẳng định nào sau đây đúng?
Đáp án: C Phương pháp giải: Hai mặt phẳng phân biệt chứa hai đường thẳng song song cắt nhau theo giao tuyến song song với hai đường thẳng đó. Lời giải chi tiết:
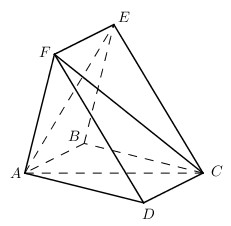
\(\left\{ \matrix{ MN//BC \hfill \cr MN \subset \left( {AMN} \right) \hfill \cr B'C' \subset \left( {ABC} \right) \hfill \cr} \right. \Rightarrow \left( {ABC} \right) \cap \left( {AMN} \right) = \Delta \) đi qua A và \(\Delta //MN//BC\). Chọn C. Câu hỏi 20 : Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Kết quả nào sau đây là đúng?
Đáp án: B Phương pháp giải: Vẽ hình, chứng minh các mặt phẳng song song. Lời giải chi tiết:
Ta có \(AD \cap \left( {BEF} \right) = A \Rightarrow A\) sai. Ta có: \(\left\{ \matrix{ AF//BE \hfill \cr AD//BC \hfill \cr} \right. \Rightarrow \left( {AFD} \right)//\left( {BEC} \right) \Rightarrow \) B đúng. \(\left( {ABD} \right) \cap \left( {EFC} \right) = CD \Rightarrow C\) sai. \(EC \cap \left( {ABF} \right) = E \Rightarrow D\) sai. Chọn B. Câu hỏi 21 : Cho tứ diện ABCD. Lấy điểm M thuộc miền trong tam giác ABC. Gọi mặt phẳng \(\left( \alpha \right)\) đi qua M và song song với BC và BD. Thiết diện tạo bởi mặt phẳng \(\left( \alpha \right)\) và tứ diện ABCD là hình gì?
Đáp án: A Phương pháp giải: Xác định thiết diện dựa vào các yếu tố song song. Lời giải chi tiết: Trong (ABC) qua M kẻ đường thẳng song song với BC cắt AB và AC lần lượt tại B’ và C’. Trong (ABD) qua B’ kẻ đường thẳng song song với BD cắt AD tại D’. Vậy \(\left( \alpha \right) \equiv \left( {B'C'D'} \right) \Rightarrow \) Thiết diện là tam giác. Chọn A.
Câu hỏi 22 : Cho tứ diện ABCD. Gọi I là trung điểm của BC, M là điểm trên cạnh DC. Một mp\(\left( \alpha \right)\) qua M, song song BC và AI. Gọi P, Q lần lượt là giao điểm của \(\left( \alpha \right)\) với BD và AD. Xét các mệnh đề sau: (1) MP // BC (2) MQ // AC (3) PQ // AI (4) (MPQ) // (ABC) Số mệnh đề đúng là:
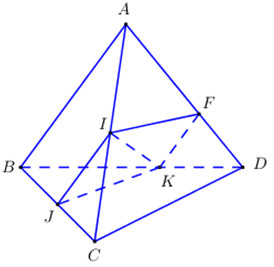
Đáp án: B Phương pháp giải: +) Với\(\left( P \right),\left( Q \right),\left( R \right)\) là 3 mặt phẳng phân biệt, có \(\left\{ \begin{array}{l}\left( P \right)//\left( Q \right)\\\left( R \right) \cap \left( P \right) = a\\\left( R \right) \cap \left( Q \right) = b\end{array} \right. \Rightarrow a//b\) +) Chứng minh hai mặt phẳng song song: \(\left\{ \begin{array}{l}a,b//\left( P \right)\\a,b \subset \left( Q \right)\\a \cap b = \left\{ I \right\}\end{array} \right. \Rightarrow \left( P \right)//\left( Q \right)\) Lời giải chi tiết: Ta có: \(\left\{ \begin{array}{l}BC,AI//\left( \alpha \right)\\BC,AI \subset \left( {ABC} \right)\\BC \cap AI = I\end{array} \right. \Rightarrow \left( \alpha \right)//\left( {ABC} \right)\) hay \(\left( {MNP} \right)//\left( {ABC} \right)\): (4) đúng Ta có: \(\left\{ \begin{array}{l}\left( {ACD} \right) \cap \left( {MNP} \right) = MQ\\\left( {ACD} \right) \cap \left( {ABC} \right) = AC\\\left( {MNP} \right)//\left( {ABC} \right)\end{array} \right. \Rightarrow MQ//AC\): (2) đúng Tương tự: MP // BC : (1) đúng (3): PQ // AI : sai (PQ // AB, mà AB khác phương AI) Chọn: B Câu hỏi 23 : Cho tứ diện \(ABCD\). Gọi \(I,\,\,J\) lần lượt là trung điểm của \(AC\) và \(BC\). Trên cạnh \(BD\) lấy điểm \(K\) sao cho \(BK = 2KD\). Gọi \(F\) là giao điểm của \(AD\) với mặt phẳng \(\left( {IJK} \right)\). Tính tỉ số \(\dfrac{{FA}}{{FD}}\).
Đáp án: B Phương pháp giải: + Dựng giao tuyến dựa vào các yếu tố song song. + Sử dụng định lí Ta-lét. Lời giải chi tiết:
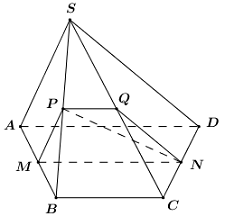
\(\left\{ \begin{array}{l}\left( {IJK} \right) \supset IJ\\\left( {ABD} \right) \supset AB\\IJ//AB\\K \in \left( {IJK} \right) \cap \left( {ABD} \right)\end{array} \right. \Rightarrow \) Giao tuyến của hai mặt phẳng \(\left( {IJK} \right)\) và \(\left( {ABD} \right)\) là đường thẳng đi qua \(K\) và song song với \(IJ,\,\,AB\). Trong \(\left( {ABD} \right)\) kẻ \(KF//AB\,\,\left( {F \in AD} \right)\), khi đó ta có \(\left( {IJK} \right) \cap \left( {ABD} \right) = KF \Rightarrow \left( {IJK} \right) \cap AD = F\). Áp dụng định lí Ta-lét ta có \(\dfrac{{FA}}{{FD}} = \dfrac{{KB}}{{KD}} = 2\). Chọn B. Câu hỏi 24 : Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình thang cân đáy lớn \(AD\). Gọi \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(AB,\,\,CD,\,\,SB\). Thiết diện của hình chóp \(S.ABCD\) cắt bởi mặt phẳng \(\left( {MNP} \right)\) là:
Đáp án: B Phương pháp giải: Dựng thiết diện có sử dụng yếu tố song song. Lời giải chi tiết:
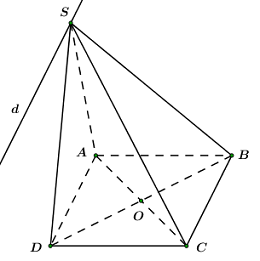
Vì \(MN\) là đường trung bình của hình thang \(ABCD \Rightarrow MN\parallel AD\parallel BC\). Ta có: \(\left\{ \begin{array}{l}\left( {MNP} \right) \supset MN\\\left( {SBC} \right) \supset BC\\MN\parallel BC\,\,\left( {cmt} \right)\\P \in \left( {MNP} \right) \cap \left( {SBC} \right)\end{array} \right. \Rightarrow \) Giao tuyến của hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {SBC} \right)\) là đường thẳng đi qua \(P\) và song song với \(MN,\,\,BC\). Gọi \(Q\) là trung điểm của \(SC \Rightarrow PQ\parallel BC\) (\(PQ\) là đường trung bình của tam giác \(SBC\)) \( \Rightarrow \left( {MNP} \right) \cap \left( {SBC} \right) = PQ\). Vậy thiết diện của hình chóp cắt bởi \(\left( {MNP} \right)\) là tứ giác \(MNQP\). Do \(PQ\parallel BC\parallel MN \Rightarrow MNQP\) là hình thang. Chọn B. Câu hỏi 25 : Cho hình chóp \(SABCD\) có đáy là hình bình hành \(ABCD.\) Giao tuyến của hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBC} \right)\) là đường thẳng song song với đường thẳng nào sau đây?
Đáp án: B Phương pháp giải: Xác định giao tuyến của hai mặt phẳng rồi chọn đáp án đúng. Lời giải chi tiết:
Ta có: \(ABCD\) là hình bình hành \( \Rightarrow AD//BC\) \( \Rightarrow \left( {SAD} \right)//\left( {SBC} \right).\) Lại có: \(\left( {SAD} \right) \cap \left( {SBC} \right) = \left\{ S \right\}.\) Qua \(S\) kẻ đường thẳng \(d\) song song với \(AD.\) \( \Rightarrow \left( {SAB} \right) \cap \left( {SBC} \right) = d.\) Chọn B. Quảng cáo
|