20 bài tập tổng hợp về Hình bình hànhLàm bàiQuảng cáo
Câu hỏi 1 : Hãy chọn câu đúng:
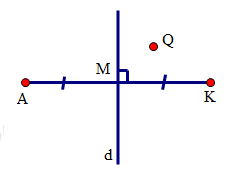
Đáp án: C Phương pháp giải: Áp dụng định nghĩa hai điểm đối xứng nhau qua trục: hai điểm A, A' được gọi là đối xứng nhau qua d nếu d là đường trung trực của AA' . Lời giải chi tiết: Ta thấy rằng d vuông góc với AK tại trung điểm M của AK , do đó d là đường trung trực của đoạn AK . Cho nên A và K đối xứng nhau qua d . Câu hỏi 2 : Trong các tứ giác sau, tứ giác nào là hình có 4 trục đối xứng?
Đáp án: B Phương pháp giải: + Dựa vào tính chất của các hình. Lời giải chi tiết: Cách giải: +) Hình vuông là tứ giác có 4 trục đối xứng. +) Hình chữ nhật có 2 trục đối xứng là hai đường trung trực của các cạnh. +) Hình bình hành không có trục đối xứng. +) Hình thoi có 2 trục đối xứng là 2 đường chéo. Chọn B .
Câu hỏi 3 : Cho đoạn thẳng AB có độ dài 3cm và đường thẳng d . Đoạn thẳng A'B' đối xứng với AB qua d . Độ dài đoạn thẳng A'B' là:
Đáp án: A Phương pháp giải: Áp dụng tính chất đoạn thẳng đối xứng với đoạn thẳng qua một đường thẳng bất kì sẽ bảo toàn độ dài. Lời giải chi tiết: Ta thấy đoạn thẳng A'B' đối xứng với AB qua d thì độ dài đoạn thẳng A'B' bằng độ dài đoạn thẳng AB . Do đó \(A'B' = AB = 3cm\) Chọn A Câu hỏi 4 : Biết rằng tam giác IKN đối xứng với tam giác MLP qua đường thẳng a theo thứ tự các đỉnh tương ứng và góc IKN bằng \({25^0}\) . Khi đó số đo góc MLP là:
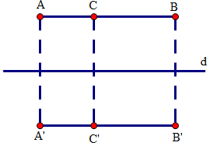
Đáp án: A Phương pháp giải: Áp dụng tính chất đối xứng trục thì hai tam giác đối xứng qua a sẽ bằng nhau. Do đó hai góc tương ứng của hai tam giác sẽ bằng nhau. Lời giải chi tiết: Do tam giác IKN đối xứng với tam giác MLP qua đường thẳng a , nên \(\widehat {IKN} = \widehat {MLP} = {25^0}\) Chọn A Câu hỏi 5 : Các điểm A’, B’, C’ đối xứng với các điểm A, B, C qua đường thẳng d . Biết rằng C nằm giữa A và \(B,AC = 2m,CB = 3m\). Độ dài đoạn thẳng A’,B’ là:
Đáp án: A Phương pháp giải: + Đầu tiên ta tính độ dài cạnh AB dựa vào giả thiết điểm C nằm giữa hai điểm A và B . + Dựa vào tính chất đối xứng ta xác định được A’B’ đối xứng với AB qua d . Do đó độ dài A’B’ bằng độ dài AB. Lời giải chi tiết: Do C nằm giữa A và B ta có: \(AB = AC + CB = 2 + 3 = 5cm\) Do A, B, C đối xứng với A’, B’, C’ qua d nên ta có \(A'B' = AB = 5cm\) Câu hỏi 6 : Tứ giác \(ABCD\) là hình bình hành nếu:
Đáp án: B Phương pháp giải: Phương pháp: Dựa vào dấu hiệu nhận biết hình bình hành: Tứ giác có các cạnh đối bằng nhau là hình bình hành Lời giải chi tiết:
Cách giải: Tứ giác \(ABCD\) là hình bình hành nếu \(AB=CD,AD=BC\) ( dấu hiệu nhận biết). Chọn B. Câu hỏi 7 : Hãy chọn câu sai:
Đáp án: C Phương pháp giải: Phương pháp: Dựa vào tính chất của hình bình hành Lời giải chi tiết: Cách giải: Theo tính chất của hình bình hành thì có: các cạnh đối bằng nhau, các góc đối bằng nhau, hai đường chéo cắt nhau tại trung điểm mỗi đường. Do đó câu sai là: Hình bình hành có hai đường chéo vuông góc với nhau. Chọn C. Câu hỏi 8 : Tỉ số độ dài hai cạnh của hình bình hành là \(3:5\) . Còn chu vi của nó bằng \(48cm\). Độ dài hai cạnh kề của hình bình hành là
Đáp án: D Phương pháp giải: Phương pháp: Gọi độ dài hai cạnh của hình bình hành là \(a\) và \(b\) rồi áp dụng tính chất dãy tỉ số bằng nhau để tìm \(a,b\) Lời giải chi tiết:
Lưu ý: Tổng của \(a,b\) là nửa chu vi hình bình hành. Cách giải: Gọi độ dài hai cạnh của hình bình hành là \(a\) và \(b\) với \(a,b>0\) . Theo bài ra ta có: \(\frac{a}{3}=\frac{b}{5}\) . Nửa chu vi của hình bình hành là: \(48:2=24cm\) . Theo tính chất của dãy tỉ số bằng nhau ta có: \(\begin{align}& \frac{a}{3}=\frac{b}{5}=\frac{a+b}{3+5}=\frac{24}{8}=3 \\& \Rightarrow a=3.3=9 \\& b=3.5=15 \\\end{align}\) Vậy hai cạnh của hình bình hành là \(9cm\) và \(15cm\) . Chọn D Câu hỏi 9 : Cho hình bình hành \(ABCD\) , gọi \(E\) là trung điểm của \(AB,\text{ }F\) là trung điểm của\(CD\) . Mối quan hệ giữa \(DE\) và \(BF\)
Đáp án: A Phương pháp giải: Phương pháp: Thông qua việc chứng minh hai tam giác bằng nhau để chỉ ra hai cạnh tương ứng bằng nhau. Lời giải chi tiết: Xét \(\Delta ADE\) và \(\Delta CBF\) có: \(\widehat{A}=\widehat{C}\) ( góc đối hình bình hành) \(AD=BC\) ( cạnh đối hình bình hành) \(AE=CF\) ( bằng nửa cạnh đối \(AB,CD\) của hình bình hành) \(\Rightarrow \Delta ADE=\Delta CBF\left( c.g.c \right)\Rightarrow DE=BF\) (cạnh tương ứng). Chọn A Câu hỏi 10 : Cho tam giác và tam giác A’, B’, C’ đối xứng nhau qua đường thẳng d biết \(AB = 4cm,BC = 7cm\) và chu vi của tam giácABC = 17cm. Khi đó độ dài cạnh C’A’ của tam giác A’B’C’ là:
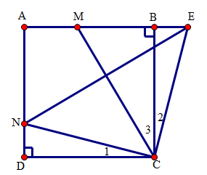
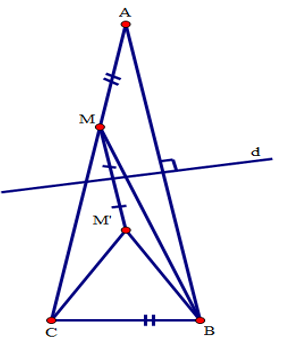
Đáp án: B Phương pháp giải: + Đầu tiên ta áp dụng công thức tính chu vi để tìm ra độ dài đoạn thẳng AC. + Theo tính chất đối xứng trục ta thấy A’C’ đối xứng với AC qua d. Do đó độ dài A’C’ bằng độ dài AC. Lời giải chi tiết: Do chu vi tam giác ABC bằng 17 nên: , suy ra \(CA = 17-AB-BC = 17-7-4 = 6\left( {cm} \right)\) Do tam giác ABC và tam giác A’B’C’ đối xứng nhau qua đường thẳng d nên \(A'C' = AC = 6\left( {cm} \right)\) Chọn B Câu hỏi 11 : Cho hình vuông ABCD cạnh bằng a. M và N là hai điểm lưu động lần lượt trên cạnh AB và AD sao cho . Vẽ tia Cx vuông góc với CN, Cx cắt đường thẳng AB tại E. Chứng minh rằng E là điểm đối xứng của N qua CM Chứng minh rằng đường cao vẽ từ C trong tam giác CMN bằng một hằng số và chu vi của tam giác AMN bằng 2a. Phương pháp giải: a) + Đầu tiên ta chứng minh CM là tia phân giác của góc NCE + Ta chứng minh ta giác NCE cân tại C, từ đó suy ra CM là tia phân giác đồng thời là trung trực củaNE. Do đó E đối xứng với N qua CM . b) + Do tính chất đối xứng trục ta suy ra đường cao vẽ từ C trong tam giác CMN bằng CB . + Để chứng minh chu vi tam giác AMN bằng 2a ta biến đổi các cạnh của tam giác để xuất hiện các cạnh của hình vuông. Từ đó chứng minh được. Lời giải chi tiết: a) Ta có \(\widehat {MCE} = {45^0}\) hay . Mà \(\widehat {{C_2}} + \widehat {{C_3}} = {45^0}\) (vì \(\widehat {MCN} = {45^0}\)) nên \(\widehat {{C_1}} = \widehat {{C_2}}\) Xét tam giác CDN và tam giác CBE có: BC = DC (do ABCD là hình vuông); \(\widehat D = \widehat B = {90^0}\) ; \(\widehat {{C_1}} = \widehat {{C_2}}\) (cmt) Suy ra \(\Delta CDN = \Delta CBE(g.c.g)\) .Suy ra CN = CE Xét tam giác CEN có CN = CE (cmt) nên tam giác CEN là tam giác cân tại C . Vậy E là điểm đối xứng của N qua CM .(đpcm) Suy ra phân giác CM đồng thời là đường trung trực của NE . b) Ta có \(\Delta CMN = \Delta CME\) (do tính đối xứng). Do đó, đường cao vẽ từ C trong tam giác CMN bằng đường cao CB = a trong tam giác CME . Ta có: MN = ME (vì \(\Delta CMN = \Delta CME\)) Suy ra chu vi tam giác AMN là: \(AM + AN + MN = AM + AN{\rm{ }} + ME = AM + AN + MB + BE\) \( = AM + AN + MB + ND\) (vì \(\Delta CDN = \Delta CBE\) nên BE = ND) \( = \left( {AM{\rm{ }} + MB} \right) + \left( {AN + ND} \right) = 2a\) Vậy chu vi tam giác AMN bằng 2a . (đpcm) Câu hỏi 12 : Cho tam giác ABC có \(\widehat A = {20^0};\widehat B = {80^0}\) , d là trung trực của cạnh AB. Trên cạnh AC, lấy điểm M sao cho AM = BC và gọi M’ là điểm đối xứng của M qua d. Chứng minh rằng tam giác M’BC là tam giác đều Tính góc BMC.Phương pháp giải: +Để chứng minh tam giác M’BC là tam giác đều ta dùng dấu hiệu tam giác cân có một góc bằng \({60^0}\) là tam giác đều + Ta thấy \(\widehat {BMC} = \widehat {CMM'} + \widehat {M'MB}\). Do đó để tính góc BMC ta lần lượt đi tính góc \(\widehat {CMM'}\) và \(\widehat {M'MB}\)
Lời giải chi tiết: a) Do tính chất đối xứng qua d , ta có AM = BM’ . Mà AM = BC (gt) nên BM’ = BC . Ta lại có \(\widehat {M'BA} = \widehat {MAB} = {20^0}\) ( do M, A đối xứng với M’, B qua d) Suy ra \(\widehat {M'BC} = \widehat B - {20^0} = {80^0} - {20^0} = {60^0}\) Xét tam giác M’BC có BM’ = BC ,\(\widehat {M'BC} = {60^0}\) do đó tam giác M’BC là tam giác đều. (đpcm) b) Ta cũng có: \(\widehat {MCB} = {180^0} - \left( {\widehat A + \widehat B} \right) = {180^0} - \left( {{{20}^0} + {{80}^0}} \right) = {80^0}\) Suy ra \(\widehat {MCM'} = \widehat {MCB} - \widehat {M'CB} = {80^0} - {60^0} = {20^0}\) Mà \(\widehat {CMM'} = \widehat A = {20^0}\) (góc đồng vị) Nên \(\widehat {MCM'} = \widehat {CMM'} = {20^ \circ }\) Suy ra \(M'C = M'M = M'B\) Ta lại có: \(\widehat {M'MB} = \widehat {M'BM}\) (tam giác M'MB cân tại đỉnh M'); \(\widehat {M'MB} = \widehat {MBA}\) (so le trong) Nên \(\widehat {M'BM} = \widehat {MBA} = {1 \over 2}\widehat {M'BA} = {10^0}\) Vậy\(\widehat {BMC} = \widehat {CMM'} + \widehat {M'MB} = {20^0} + {10^0} = {30^0}\)
Câu hỏi 13 : Chọn câu đúng. Hình nào sau đây có 4 trục đối xứng ?
Đáp án: A Phương pháp giải: Sử dụng kiến thức: trục đối xứng của các đa giác Lời giải chi tiết: Ta có +) Hình chữ nhật có 2 trục đối xứng. +) Hình thoi có 2 trục đối xứng. +) Hình bình hành không có trục đối xứng. +) Hình vuông có 4 trục đối xứng. Chọn A. Câu hỏi 14 : Cho hình bình hành \(ABCD\) có \(\widehat{A}=3\widehat{B}\) . Số đo các góc của hình bình hành là:
Đáp án: D Phương pháp giải: Phương pháp: Dựa vào tính chất hình bình hành và định lí tổng các góc trong một tứ giác Lời giải chi tiết: Cách giải: Trong hình bình hành \(ABCD\) có: \(\widehat{A}=\widehat{C},\widehat{B}=\widehat{D}\) (tính chất), \(\widehat{A}=3\widehat{B}\) Theo định lí tổng các góc trong tứ giác ta có: \(\begin{align} & \widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360{}^\circ \Rightarrow 2\left( \widehat{A}+\widehat{B} \right)=360{}^\circ \Rightarrow \widehat{A}+\widehat{B}=180{}^\circ \Rightarrow 3\widehat{B}+\widehat{B}=180{}^\circ \Rightarrow \widehat{B}=45{}^\circ \\ & \Rightarrow \widehat{A}=3\widehat{B}=3.45{}^\circ =135{}^\circ \\ \end{align}\) Chọn D Câu hỏi 15 : Tính số đo các góc của hình bình hành \(ABCD\) biết \(\widehat{A}-\widehat{B}=40{}^\circ \) . Ta được:
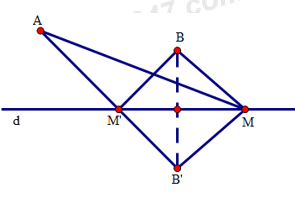
Đáp án: A Phương pháp giải: Phương pháp: Dựa vào tính chất hình bình hành và định lí tổng các góc trong một tứ giác Lời giải chi tiết: Cách giải: Trong hình bình hành \(ABCD\) có: \(\widehat{A}=\widehat{C},\widehat{B}=\widehat{D}\) (tính chất), \(\widehat{A}-\widehat{B}=40{}^\circ (gt)\Rightarrow \widehat{A}=40{}^\circ +\widehat{B}\) Theo định lí tổng các góc trong tứ giác ta có: \(\begin{array}{l}\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \Rightarrow 2\left( {\widehat A + \widehat B} \right) = 360^\circ \Rightarrow \widehat A + \widehat B = 180^\circ \Rightarrow 40^\circ + \widehat B + \widehat B = 180^\circ \Rightarrow \widehat B = 70^\circ \\ \Rightarrow \widehat A = 40^\circ + \widehat B = 40^\circ + 70^\circ = 110^\circ \end{array}\) Chọn A. Câu hỏi 16 : Cho hình bình hành \(ABCD\) . Tia phân giác của góc \(A\) cắt \(CD\) tại \(M\) . Tia phân giác góc \(C\) cắt \(AB\) tại \(N\) . Tứ giác \(AMCN\) là hình gì?
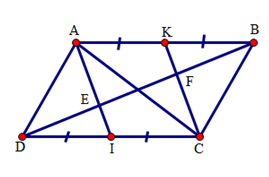
Đáp án: B Phương pháp giải: Phương pháp: Sử dụng dấu hiệu nhận biết tứ giác có các cạnh đối song song là hình bình hành. Lời giải chi tiết: Vì \(\widehat{NAM}=\frac{1}{2}\widehat{A},\widehat{MCN}=\frac{1}{2}\widehat{C}\) mà \(\widehat{A}=\widehat{C}\) ( góc đối hình bình hành) nên \(\widehat{NAM}=\widehat{MCN}\) Lại có \(\widehat{BNC}=\widehat{MCN}\) ( so le trong, \(AB\parallel CD\) ) Suy ra \(\widehat{NAM}=\widehat{BNC}\) . Mà hai góc \(\widehat{NAM},\widehat{BNC}\) ở vị trí đồng vị nên \(AM\parallel CN\) . Do \(AB\parallel CD(gt),N\in AB,M\in BC\Rightarrow AN\parallel MC\) Tứ giác \(AMCN\) có \(AN\parallel CM,AM\parallel CN(cmt)\) nên là hình bình hành (dấu hiệu nhận biết). Chọn B Câu hỏi 17 : Cho hình bình hành \(ABCD\) . Gọi \(I,\text{ }K\) theo thứ tự là trung điểm của \(CD,\text{ }AB\) . Đường chéo \(BD\) cắt \(AI,\text{ }CK\) theo thứ tự ở \(E,\text{ }F\) .Mối quan hệ giữa DE, FE, FB.
Đáp án: A Phương pháp giải: Phương pháp: Chứng minh tứ giác \(AKCI\) là hình bình hành để suy ra \(AI\parallel CK\) . Sau đó sử dụng định lí đường trung bình của các tam giác \(\Delta DCF,\Delta ABE\) để suy ra điều phải chứng minh. Lời giải chi tiết: Vì \(AK=\frac{AB}{2},IC=\frac{CD}{2}\) (gt) mà \(AB=CD\) (cạnh đối hình bình hành) nên \(AK=IC\) . Vì \(AB\parallel CD(gt),K\in AB,I\in DC\Rightarrow AK\parallel IC\) . Tứ giác \(AKCI\) có \(AK\parallel CI,AK=IC(cmt)\) nên là hình bình hành. Suy ra \(AI\parallel CK\) Mà \(E\in AI,F\in CK\Rightarrow EI\parallel CF,KF\parallel AE\) . Xét \(\Delta DCF\) có: \(DI=IC(gt),IE\parallel CF(cmt)\Rightarrow ED=FE(1)\) Xét \(\Delta ABE\) có: \(AK=KB(gt),KF\parallel AE(cmt)\Rightarrow EF=FB(2)\). Từ (1) và (2) suy ra \(ED=FE=FB\) . Chọn A Câu hỏi 18 : Cho hình bình hành \(ABCD\) . Trên đường chéo \(BD\) lấy hai điểm \(E\) và \(F\) sao cho \(BE=DF<\frac{1}{2}BD\) . a) Chứng minh \(FA=CE\) . b) Tia \(AE\) cắt \(BC\) tại \(I\) , tia \(CF\) cắt \(AD\) tại \(K\) . Chứng minh rằng ba đường thẳng \(AC,\text{ }BD,\text{ }IK\) đồng quy. Phương pháp giải: Phương pháp: a) Chứng minh tứ giác \(AECF\) là hình bình hành để suy ra. b) Dự đoán ba đường thẳng đồng quy tại giao điểm của hai đường chéo hình bình hành \(ABCD\). Lời giải chi tiết: a) Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Ta có \(OA=OC,OB=OD\) . Mà \(BE=DF(gt)\Rightarrow OE=FO\) . Tứ giác \(AECF\) có hai đường chéo \(AC\) và \(EF\) cắt nhau tại trung điểm \(O\) nên \(AECF\) là hình bình hành \(\Rightarrow FA=CE\) . b) Theo câu a) tứ giác AECF là hình bình hành nên \(EA\parallel CF\Rightarrow AI\parallel CK\) . Do \(BC\parallel AD(gt),K\in AD,I\in BC\Rightarrow AK\parallel CI\) . Tứ giác \(AICK\) có các cạnh đối song song nên là hình bình hành. Do đó \(IK\) cắt \(AC\) tại \(O\) là giao điểm của \(AC\) và \(BD\). Suy ra ba đường thẳng \(AC,BD,IK\) đồng quy. Câu hỏi 19 : Cho hai điểm A, B nằm trên cùng một nửa mặt phẳng bờ là đường thẳng d. Tìm trên đường thẳng d điểm M sao cho tổng MA + MB nhỏ nhất. Phương pháp giải: Ta nhân thấy nếu A, B nằm trên hai nửa mặt phẳng đối nhau bờ là đường thẳng d thì tổng MA + MB nhỏ nhất là đoạn AB . Do vậy ta tìm cách đưa bài toán về trường hợp này. Bằng cách dựng B’ đối xứng với B qua d ta đưa bài toán đã cho về trường hợp nêu trên vì MB = MB’ . Lời giải chi tiết: Gọi B’ là điểm đối xứng của B qua đường thẳng d. B’ cố định. Ta có MB = MB’ (tính chất đối xứng trục). Xét ba điểm M, A, B’ ta có \(MA + MB' \ge AB'\) Do đó \(MA + MB \ge AB'\) Câu hỏi 20 : Cho hình bình hành \(ABCD\) có \(\widehat{A}=\alpha >90{}^\circ \) . Ở phía ngoài hình bình hành vẽ các tam giác đều \(ADE,ABF\). a) \(\widehat{EAF}\) bằng bao nhiêu ? b)tam giác \(CEF\) là tam giác gì?
Đáp án: A Phương pháp giải: Phương pháp: Để chứng minh tam giác đều ta đi chứng minh ba cạnh bằng nhau dựa vào từng cặp cạnh bằng nhau được suy ra từ các tam giác bằng nhau. Lời giải chi tiết: a) Ta có: \(\begin{align} & \widehat{EAF}=360{}^\circ -\widehat{BAF}-\widehat{EAD}-\alpha \\ & =360{}^\circ -60{}^\circ -60{}^\circ -\alpha =240{}^\circ -\alpha \\ \end{align}\) b) Ta có:\(\begin{align} & \widehat{ADC}=180{}^\circ -\alpha \\ & \widehat{CDE}=\widehat{ADC}+\widehat{EDA}=180{}^\circ -\alpha +60{}^\circ =240{}^\circ -\alpha \\ & \Rightarrow \widehat{CDE}=\widehat{FAE} \\ \end{align}\) Xét \(\Delta CDE\) và \(\Delta FAE\) có: \(\begin{align} & CD=FA(gt) \\ & \widehat{CDF}=\widehat{EAF}(cmt) \\ & DE=EA(gt) \\ & \Rightarrow \Delta CDE=\Delta FAE\left( c.g.c \right)\Rightarrow CE=FE(1) \\ \end{align}\) Tương tự : Ta có: \(\begin{align}& \widehat{ABC}=180{}^\circ -\alpha \\& \widehat{CBF}=\widehat{ABC}+\widehat{FBA}=180{}^\circ -\alpha +60{}^\circ =240{}^\circ -\alpha \\& \Rightarrow \widehat{CBF}=\widehat{FAE} \\\end{align}\) Xét \(\Delta FBC\) và \(\Delta FAE\) có: \(\begin{align}& FB=FA(gt) \\& \widehat{CBF}=\widehat{EAF}(cmt) \\& CB=EA(gt) \\& \Rightarrow \Delta FBC=\Delta FAE\left( c.g.c \right)\Rightarrow CF=FE(2) \\\end{align}\) Từ (1) và (2) suy ra \(CF=FE=EC\) nên tam giác \(CEF\) đều. Chọn A. Quảng cáo
|