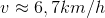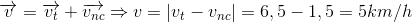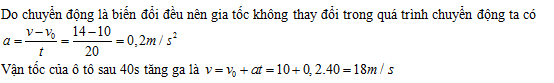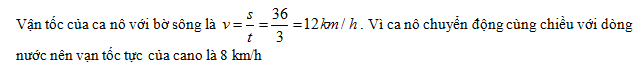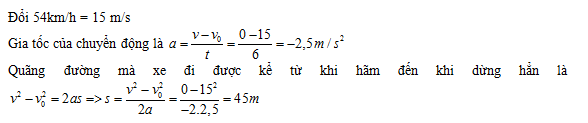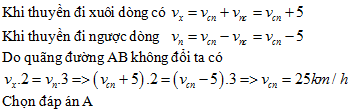Lời giải chi tiết:

Vì thuyền chuyển động ngược chiều dòng nước nên từ công thức cộng vận tốc ta có vận tốc của thuyền đối với bờ sông là

Lời giải chi tiết:

Phương pháp giải:

Lời giải chi tiết:

Lời giải chi tiết:

Phương pháp giải:

Phương pháp:

Công thức cộng vận tốc: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

Lời giải chi tiết:

Cách giải:

Người và tàu chuyển động vuông góc với nhau nên vận tốc của người đó so với mặt đất là:

\({v_{13}} = \sqrt {v_{12}^2 + v_{23}^2}  = \sqrt {{{10}^2} + {1^2}}  = 10,05m/s\)

Chọn C

Lời giải chi tiết:

Phương pháp giải:

Vật (1) : Vật chuyển động

Vật (2): Hệ quy chiếu chuyển động

Vật (3): Hệ quy chiếu đứng yên.

Ta có:

 + \(\overrightarrow {{v_{12}}} \): vận tốc của vật chuyển động (1) so với hệ quy chiếu chuyển động (2) → Vận tốc tương đối

 + \(\overrightarrow {{v_{13}}} \): vận tốc của vật chuyển động (1) so với hệ quy chiếu đứng yên (3) → Vận tốc tuyệt đối

 + \(\overrightarrow {{v_{23}}} \): vận tốc của hệ quy chiếu chuyển động (2) so với hệ quy chiếu chuyển động (3) → Vận tốc kéo theo.

Công thức cộng vận tốc: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

Lời giải chi tiết:

Vật (1): cano; Vật (2): dòng nước; Vật (3): bờ sông.

Thời gian cano đi từ bến A đến bến B là: \(t = \dfrac{{AB}}{{{v_{13}}}}\)

+ Cano đi xuôi dòng \( \Rightarrow \overrightarrow {{v_{12}}} \, \uparrow  \uparrow \,\,\overrightarrow {{v_{23}}} \)

→ Độ lớn vận tốc của cano so với bờ sông là: \({v_{13}} = {v_{12}} + {v_{23}} = {v_{12}} + 10\,\,\left( {km/h} \right)\)

Thời gian đi xuôi dòng là: \({t_x} = \dfrac{{AB}}{{{v_{12}} + 5}} = 4\,\,\left( h \right)\,\,\,\,\,\,\,\,\left( * \right)\)

+ Cano đi ngược dòng \( \Rightarrow \overrightarrow {{v_{12}}} \, \uparrow  \downarrow \,\,\overrightarrow {{v_{23}}} \,\,\,\left( {{v_{12}} > {v_{23}}} \right)\)

→ Độ lớn vận tốc của cano so với bờ sông là: \({v_{13}}' = {v_{12}} - {v_{23}} = {v_{12}} - 10\,\,\left( {km/h} \right)\)

Thời gian đi ngược dòng là: \({t_n} = \dfrac{{AB}}{{{v_{12}} - 5}} = 9\,\,\left( h \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {**} \right)\)

Từ (1) và (2) ta có: \(\dfrac{{\left( * \right)}}{{\left( {**} \right)}} \Leftrightarrow \dfrac{{{v_{12}} - 10}}{{{v_{12}} + 10}} = \dfrac{4}{9} \Rightarrow {v_{12}} = 26\,\left( {km/h} \right)\)

Chọn C

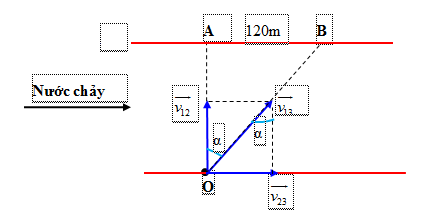
Phương pháp giải:

Vật (1) : Vật chuyển động

Vật (2): Hệ quy chiếu chuyển động

Vật (3): Hệ quy chiếu đứng yên.

Ta có:

 + \(\overrightarrow {{v_{12}}} \): vận tốc của vật chuyển động (1) so với hệ quy chiếu chuyển động (2) → Vận tốc tương đối

 + \(\overrightarrow {{v_{13}}} \): vận tốc của vật chuyển động (1) so với hệ quy chiếu đứng yên (3) → Vận tốc tuyệt đối

 + \(\overrightarrow {{v_{23}}} \): vận tốc của hệ quy chiếu chuyển động (2) so với hệ quy chiếu chuyển động (3) → Vận tốc kéo theo.

Công thức cộng vận tốc: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

Lời giải chi tiết:

Vật (1): Tàu thuỷ; Vật (2): dòng nước; Vật (3): bờ sông.

Với \(\overrightarrow {{v_{12}}} \,\)là vận tốc của tàu so với nước; \(\,\,\overrightarrow {{v_{23}}} \) là vận tốc của nước so với bờ.

Thời gian chuyển động là: \(t = \dfrac{{AB}}{{{v_{13}}}}\)

+ Tàu đi xuôi dòng ta có \(\overrightarrow {{v_{12}}} \, \uparrow  \uparrow \,\,\overrightarrow {{v_{23}}} \)

Vận tốc của tàu so với bờ là: \({v_{13}} = {v_{12}} + {v_{23}}\)

mà \({v_{13}} = \dfrac{{{S_1}}}{{{t_x}}} = \dfrac{{100}}{4} = 25km/h \Rightarrow {v_{12}} + {v_{23}} = 25\,\,\left( {km/h} \right)\,\,\,\left( * \right)\)

+ Tàu đi ngược dòng ta có: \(\overrightarrow {{v_{12}}} \, \uparrow  \downarrow \,\,\overrightarrow {{v_{23}}} \)

Vận tốc của tàu so với bờ là: \({v_{13}}' = {v_{12}} - {v_{23}}\)

mà \({v_{13}}' = \dfrac{{{S_2}}}{{{t_x}}} = \dfrac{{60}}{4} = 15km/h \Rightarrow {v_{12}} - {v_{23}} = 15\,\,\left( {km/h} \right)\,\,\,\left( {**} \right)\)

Từ (*) và (**) ta có: \(\left\{ \begin{array}{l}{v_{12}} + {v_{23}} = 25\\{v_{12}} - {v_{23}} = 15\end{array} \right.\, \Rightarrow \left\{ \begin{array}{l}{v_{12}} = 20km/h\\{v_{23}} = 5km/h\end{array} \right.\)

→ Vận tốc của nước so với bờ là v₂₃ = 5 km/h

Chọn A

Phương pháp giải:

Vật (1) : Vật chuyển động

Vật (2): Hệ quy chiếu chuyển động

Vật (3): Hệ quy chiếu đứng yên.

Ta có:

 + \(\overrightarrow {{v_{12}}} \): vận tốc của vật chuyển động (1) so với hệ quy chiếu chuyển động (2) → Vận tốc tương đối

 + \(\overrightarrow {{v_{13}}} \): vận tốc của vật chuyển động (1) so với hệ quy chiếu đứng yên (3) → Vận tốc tuyệt đối

 + \(\overrightarrow {{v_{23}}} \): vận tốc của hệ quy chiếu chuyển động (2) so với hệ quy chiếu chuyển động (3) → Vận tốc kéo theo.

Công thức cộng vận tốc: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

Lời giải chi tiết:

Vật (1): Thuyền

Vật (2): Dòng nước

Vật (3): Bờ sông

Ta có: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

Người chèo thuyền qua sông với vận tốc 5,4km/h là: \({v_{12}} = 9km/h = 2,5m/s\)

(Vận tốc của thuyền khi nước đứng yên)

Có \(\overrightarrow {{v_{12}}}  \bot \overrightarrow {{v_{23}}} \)

Ta có: \(\left\{ \begin{array}{l}OA = 600m{\rm{ }}\\AB = 120m\end{array} \right. \Rightarrow \tan \alpha  = \dfrac{{AB}}{{OA}} = \dfrac{{120}}{{600}} = \dfrac{1}{5}\)

Mặt khác: \(\tan \alpha  = \dfrac{{{v_{23}}}}{{{v_{12}}}} \Rightarrow {v_{23}} = {v_{12}}.\tan \alpha  = 2,5.\dfrac{1}{5} = 0,5m/s\)

Chọn B

Phương pháp giải:

Phương pháp:

Công thức cộng vận tốc: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

Lời giải chi tiết:

Cách giải:

Gọi canô  là số 1; nước số 2; bờ là số 3

Vận tốc của cano đối với bờ là: \({v_{13}} = \frac{{AB}}{t} = \frac{{36}}{{1,5}} = 24km/h\)

Vận tốc của cano đối với dòng chảy là: v₁₂

Vận tốc của nước đối với bờ là: v₂₃

Ta có: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

Cano chạy xuôi dòng nên vận tốc của cano đối với dòng chảy là:

\({v_{13}}\; = {v_{12}}\; + {\rm{ }}{v_{23}}\; \Rightarrow {v_{12}}\; = {v_{13}}\; - {v_{23}} = 24 - 6 = 18{\rm{ }}km/h\)

Chọn D

Lời giải chi tiết:

Vì khúc gỗ trôi xuôi theo dòng sông nên vận tốc của nước chính là vận tốc khúc gỗ trôi bằng 2km/h.

Gọi vận tốc của cano là v

quãng đường mà cano đi được trong 1h là s = ( v-2 ) = 20 => v = 22km/h

Phương pháp giải:

Lời giải chi tiết:

Lời giải chi tiết:

Phương pháp giải:

Phương pháp:

Áp dụng công thức cộng vận tốc: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

Lời giải chi tiết:

Cách giải:

Đổi t₁ = 1h = 3600s, S₁ = 10km = 10000m, t₂ = 1 phút = 60s

Gọi thuyền là số 1; nước số 2; bờ là số 3

Vận tốc của thuyền so với bờ có độ lớn là: \({v_{13}} = \frac{{{s_1}}}{{{t_1}}} = \frac{{1000}}{{3600}} = \frac{{25}}{9}m/s\)

Vận tốc của nước so với bờ có độ lớn là: \({v_{23}} = \frac{{{s_2}}}{{{t_2}}} = \frac{{\frac{{100}}{3}}}{{60}} = \frac{5}{9}m/s\)

Áp dụng công thức cộng vận tốc ta có: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

Chọn chiều dương là chiều chảy của dòng nước

Vì thuyền chảy ngược dòng nước nên \(\overrightarrow {{v_{13}}} ;\overrightarrow {{v_{12}}} \) hướng ngược chiều dương, \(\overrightarrow {{v_{23}}} \) hướng theo chiều dương quy ước

Suy ra: \( - {v_{13}} =  - {v_{12}} + {v_{23}} \Rightarrow {v_{12}} = {v_{13}} + {v_{23}} = \frac{{25}}{9} + \frac{5}{9} = \frac{{10}}{3}m/s = 12km/h\)

Vậy vận tốc của thuyền buồm so với nước là 12km/h

Chọn C

Phương pháp giải:

Lời giải chi tiết:

Phương pháp giải:

Phương pháp:

Công thức cộng vận tốc: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

Khi cùng chiều: v₁₃ = v₁₂ + v₂₃

Khi ngược chiều: v₁₃ = v₁₂ – v₂₃

Lời giải chi tiết:

Cách giải:

Gọi canô là 1; nước là 2; bờ là 3; ta có: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

- Lúc cano đi xuôi dòng từ A → B:

  + Vận tốc canô đối với bờ là: v₁₃ = 16,2 + 5,4 = 21,6 km/h

  + Thời gian canô xuôi dòng là: \({t_1} = \frac{{AB}}{{{v_{13}}}} = \frac{{18}}{{21,6}} = \frac{5}{6}h\)

- Lúc canô ngược dòng từ B → A:

  + Vận tốc canô đối với bờ là: v₁₃’ = 16,2 - 5,4 = 10,8 km/h

  + Thời gian canô ngược dòng là: \({t_2} = \frac{{AB}}{{{v_{13}}'}} = \frac{{18}}{{10,8}} = \frac{5}{3}h\)

- Thời gian tổng cộng cả đi và về là: \(t = {t_1} + {t_2} = \frac{5}{6} + \frac{5}{3} = 2,5h\)

Chọn C

Phương pháp giải:

Áp dụng công thức cộng vận tốc:    

\(\overrightarrow {{v_{tb}}} = \overrightarrow {{v_{tn}}} + \overrightarrow {{v_{nb}}} \)

Lời giải chi tiết:

Tóm tắt:

V_tn = 20km/h ; V_nb = 2 km/h

a) Tính vận tốc của ca nô so với bờ sông khi nó chuyển động xuôi dòng nước?

b) Tính vận tốc của ca nô so với bờ sông khi nó chuyển động ngược dòng nước?

Giải:

Áp dụng công thức cộng vận tốc:

 \(\overrightarrow {{v_{tb}}} = \overrightarrow {{v_{tn}}} + \overrightarrow {{v_{nb}}} \)

a) Khi ca nô chuyển động xuôi dòng nước thì  

\(\overrightarrow {{v_{tn}}} \uparrow \uparrow \overrightarrow {{v_{nb}}} \Rightarrow {v_{tb}} = {v_{tn}} + {v_{nb}} = 20 + 2 = 22{\rm{ }}km/h\)

b) Khi nó chuyển động ngược dòng nước thì  

\(\overrightarrow {{v_{tn}}} \uparrow \downarrow \overrightarrow {{v_{nb}}} \Rightarrow {v_{tb}} = {v_{tn}} - {v_{nb}} = 20 - 2 = 18{\rm{ }}km/h\)

Phương pháp giải:

Phương pháp:

Công thức cộng vận tốc: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

Khi cùng chiều: v₁₃ = v₁₂ + v₂₃

Khi ngược chiều: v₁₃ = v₁₂ – v₂₃

Lời giải chi tiết:

Cách giải:

Vận tốc của thuyền so với dòng nước: v₁₂ = 20km/h = 5,56m/s

Khi thuyền chuyển động xuôi dòng: \({v_{13}}\; = {v_{12}}\; + {\rm{ }}{v_{23}}\; = 5,56 + 1,25 = 6,81{\rm{ }}m/s\)

→ Thời gian xuôi dòng từ M đến N là: \({t_1} = \frac{{MN}}{{{v_{13}}}} = \frac{{MN}}{{6,81}}\)

Khi thuyền chuyển động  ngược dòng: \({v_{13}}' = {v_{12}}--{v_{23}}\; = 5,56 - 1,25 = 4,31{\rm{ }}m/s\)

→ Thời gian thuyền chạy ngược dòng từ M đến N là: \({t_2} = \frac{{MN}}{{{v_{13}}'}} = \frac{{MN}}{{4,31}}\)

Theo đề bài thời gian tổng cộng là 4 giờ = 14 400 s nên:

\({t_1} + {t_2} = 14400 \Leftrightarrow \frac{{MN}}{{6,81}} + \frac{{MN}}{{4,31}} = 14400 \Rightarrow MN = 380007m \approx 38km\)

Chọn A

Phương pháp giải:

Phương pháp:

Công thức cộng vận tốc: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

Lời giải chi tiết:

Cách giải:

Chọn chiều dương là chiều chuyển động của tàu A

Gọi:  + \(\overrightarrow {{v_{BD}}} \) vận tốc của tàu B đối với đất, \(\overrightarrow {{v_{BD}}} \) ngược chiều dương nên v_BD = -10 km/h

        +  \(\overrightarrow {{v_{AD}}} \) vận tốc của tàu A đối với đất, \(\overrightarrow {{v_{AD}}} \)theo chiều dương nên v_AD = 15 km/h

        + \(\overrightarrow {{v_{BA}}} \) vận tốc của tàu B đối với tàu A

Theo công thức cộng vận tốc: \(\overrightarrow {{v_{BA}}}  = \overrightarrow {{v_{BD}}}  + \overrightarrow {{v_{DA}}}  = \overrightarrow {{v_{BD}}}  - \overrightarrow {{v_{AD}}} \)

\( \Rightarrow {v_{BA}} = {v_{BD}} - {v_{AD}} =  - 10 - 15 =  - 25\,km/h\)

Chứng tỏ vận tốc của tàu B so với tàu A có độ lớn 25km/h và ngược chiều so với chiều chuyển động của tàu A

Chọn C

Phương pháp giải:

Phương pháp:

Công thức cộng vận tốc: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

Lời giải chi tiết:

Cách giải:

Chọn chiều dương là chiều chuyển động của 2 xe

Gọi   + \(\overrightarrow {{v_{AD}}} \) vận tốc của xe A đối với đất

        + \(\overrightarrow {{v_{BD}}} \)vận tốc của xe B đối với đất

        + \(\overrightarrow {{v_{BA}}} \)vận tốc của xe B đối với xe A

        + \(\overrightarrow {{v_{AB}}} \)Vận tốc của xe A đối với xe B

Theo công thức cộng vận tốc:  \(\overrightarrow {{v_{AB}}}  = \overrightarrow {{v_{AD}}}  + \overrightarrow {{v_{DB}}}  = \overrightarrow {{v_{AD}}}  - \overrightarrow {{v_{BD}}} \)

Do hai xe chuyển động cùng chiều nên: v_AB = 40 – 60 = - 20 (km/h)

→ \(\overrightarrow {{v_{AB}}} \) hướng ngược chiều dương.

Chọn B