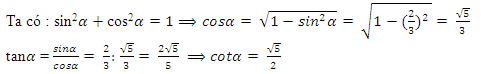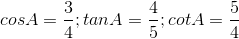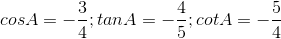20 bài tập Tính giá trị biểu thức lượng giácLàm bàiQuảng cáo
Câu hỏi 1 : Với góc nhọn \(\alpha \) tùy ý, khẳng định nào sau đây là Sai?
Đáp án: A Phương pháp giải: Sử dụng các công thức tỉ số lượng giác của góc nhọn trong tam giác vuông. Lời giải chi tiết: Ta có các công thức: \(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }};\) \(\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }};\) \(\tan \alpha .\cot \alpha = 1;\) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1.\) Vậy chỉ có đáp án A sai. Chọn A. Câu hỏi 2 : Khẳng định nào dưới đây là đúng?
Đáp án: A Phương pháp giải: Áp dụng các công thức lượng giác cơ bản. Lời giải chi tiết: +) Đáp án A: đúng +) Đáp án B: sai, công thức đúng: \({\sin ^2}\alpha + co{s^2}\alpha = 1\) +) Đáp án C: sai, công thức đúng: \(\tan \alpha = \cot \left( {{{90}^0} - \alpha } \right)\) +) Đáp án D: sai, công thức đúng: \(\cot \alpha = \tan \left( {{{90}^0} - \alpha } \right)\) Chọn A Câu hỏi 3 : Không dùng MTBT hoặc bảng số, hãy sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần. Câu 1: \(\cos {\rm{ }}{44^o},{\rm{ sin }}{50^o},{\rm{ sin }}{70^o},{\rm{ cos }}{55^o}\)
Đáp án: C Phương pháp giải: Áp dụng \(0 < \alpha < \beta < {90^0} \Rightarrow \left\{ \begin{array}{l}\sin \alpha < \sin \beta \\cos\alpha > cos\beta \end{array} \right..\) Ta có: \(\alpha + \beta = {90^0} \Rightarrow \left\{ \begin{array}{l}\sin \alpha = \cos \beta \\\cos \alpha = \sin \beta \end{array} \right.\) Lời giải chi tiết: \(\cos {\rm{ }}{44^o},{\rm{ sin }}{50^o},{\rm{ sin }}{70^o},{\rm{ cos }}{55^o}\) Ta có: \(\left\{ \begin{array}{l}\cos {\rm{ }}{44^0} = \cos {\rm{ }}\left( {{{90}^0} - {{46}^0}} \right) = {\rm{sin 4}}{{\rm{6}}^0}\\\cos {\rm{ 5}}{{\rm{5}}^0} = \cos {\rm{ }}\left( {{{90}^0} - {{35}^0}} \right) = {\rm{sin 3}}{{\rm{5}}^0}\end{array} \right.\) Vì \({35^0} < {46^0} < {50^0} < {70^0}\)\( \Rightarrow {\rm{sin 3}}{5^o} < \sin {\rm{ }}{46^o} < {\rm{sin }}{50^o} < {\rm{sin }}{70^o}\) \( \Rightarrow {\rm{cos }}{55^o} < \cos {\rm{ }}{44^o} < {\rm{sin }}{50^o} < {\rm{sin }}{70^o}.\) Chọn C. Câu 2: \({\rm{sin }}{49^o},{\rm{ cos }}{15^o},{\rm{ sin }}{65^o},{\rm{ cos }}{50^o},{\rm{ }}\cos {\rm{ }}{42^o}\)
Đáp án: B Phương pháp giải: Áp dụng \(0 < \alpha < \beta < {90^0} \Rightarrow \left\{ \begin{array}{l}\sin \alpha < \sin \beta \\cos\alpha > cos\beta \end{array} \right..\) Ta có: \(\alpha + \beta = {90^0} \Rightarrow \left\{ \begin{array}{l}\sin \alpha = \cos \beta \\\cos \alpha = \sin \beta \end{array} \right.\) Lời giải chi tiết: \({\rm{sin }}{49^o},{\rm{ cos }}{15^o},{\rm{ sin }}{65^o},{\rm{ cos }}{50^o},{\rm{ }}\cos {\rm{ }}{42^o}\) Ta có: \(\left\{ \begin{array}{l}sin{\rm{ }}{49^0} = \cos {\rm{ }}\left( {{{90}^0} - {{41}^0}} \right) = {\rm{sin 4}}{{\rm{1}}^0}\\sin{\rm{ 6}}{{\rm{5}}^0} = \cos {\rm{ }}\left( {{{90}^0} - {{25}^0}} \right) = {\rm{sin 2}}{{\rm{5}}^0}\end{array} \right.\) Vì \({15^0} < {25^0} < {41^0} < {42^0} < {50^0}\)\( \Rightarrow \cos {\rm{ }}{50^o} < \cos {\rm{ }}{42^o}{\rm{ < }}\cos {\rm{ 4}}{{\rm{1}}^o}{\rm{ < }}\cos {\rm{ 2}}{{\rm{5}}^o} < \cos {15^0}\) \( \Rightarrow {\rm{cos }}{50^0} < \cos {\rm{ }}{42^0} < {\rm{sin }}{49^0} < {\rm{sin }}{65^0}{\rm{ < cos }}{15^0}\) Chọn B. Câu hỏi 4 : Tính các tỷ số lượng giác còn lại của \(\alpha \) với \(0 < \alpha < {90^0}\) biết: Câu 1: \(\sin \alpha = \frac{2}{3}\)
Đáp án: C Phương pháp giải: Sử dụng công thức lượng giác: \(\left\{ \begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\tan \alpha .\cot \alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\end{array} \right..\) Lời giải chi tiết: Ta có: \(0 < \alpha < {90^0}\) \( \Rightarrow \left\{ \begin{array}{l}\sin \alpha > 0\\\cos \alpha > 0\\\tan \alpha > 0\\\cot \alpha > 0\end{array} \right..\) \(\sin \alpha = \frac{2}{3}\) *\({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)\( \Leftrightarrow {\left( {\frac{2}{3}} \right)^2} + {\cos ^2}\alpha = 1\)\( \Leftrightarrow {\cos ^2}\alpha = 1 - \frac{4}{9} = \frac{5}{9}\)\( \Rightarrow \cos \alpha = \frac{{\sqrt 5 }}{3}\) *\(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{2}{3}:\frac{{\sqrt 5 }}{3} = \frac{{2\sqrt 5 }}{5}\) *\(\cot \alpha = \frac{1}{{\tan \alpha }} = 1:\frac{{2\sqrt 5 }}{5} = \frac{{\sqrt 5 }}{2}\) Chọn C. Câu 2: \(\tan \alpha = \frac{4}{3}\)
Đáp án: B Phương pháp giải: Sử dụng công thức lượng giác: \(\left\{ \begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\tan \alpha .\cot \alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\end{array} \right..\) Lời giải chi tiết: Ta có: \(0 < \alpha < {90^0}\) \( \Rightarrow \left\{ \begin{array}{l}\sin \alpha > 0\\\cos \alpha > 0\\\tan \alpha > 0\\\cot \alpha > 0\end{array} \right..\) \(\tan \alpha = \frac{4}{3}\) * \(\tan \alpha .\cot \alpha = 1\)\( \Leftrightarrow \cot \alpha = 1:tan\alpha = 1:\frac{4}{3} = \frac{3}{4}\) * \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\)\( \Leftrightarrow 1 + {\left( {\frac{4}{3}} \right)^2} = \frac{1}{{{{\cos }^2}\alpha }}\)\( \Leftrightarrow \frac{1}{{{{\cos }^2}\alpha }} = \frac{{25}}{9}\)\( \Rightarrow {\cos ^2}\alpha = \frac{9}{{25}}\)\( \Rightarrow \cos \alpha = \frac{3}{5}\) *\({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)\( \Leftrightarrow {\left( {\frac{3}{5}} \right)^2} + {\sin ^2}\alpha = 1\)\( \Leftrightarrow {\sin ^2}\alpha = 1 - \frac{9}{{25}} = \frac{{16}}{{25}}\)\( \Rightarrow \sin \alpha = \frac{4}{5}\) Chọn B. Câu hỏi 5 : Tính các tỷ số lượng giác còn lại của \(\alpha \) biết: Câu 1: \(\sin \alpha = \frac{5}{{13}}\)
Đáp án: B Phương pháp giải: Sử dụng công thức lượng giác: \(\left\{ \begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\tan \alpha .\cot \alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\end{array} \right.\) Lời giải chi tiết: \(\sin \alpha = \frac{5}{{13}}\) Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Leftrightarrow {\left( {\frac{5}{{13}}} \right)^2} + {\cos ^2}\alpha = 1\)\( \Leftrightarrow {\cos ^2}\alpha = 1 - \frac{{25}}{{169}} = \frac{{144}}{{169}}\)\( \Rightarrow \cos \alpha = \pm \frac{{12}}{{13}}\) Lại có: \({\tan ^2}\alpha + 1 = \frac{1}{{{{\cos }^2}\alpha }}\) \( \Leftrightarrow {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }} - 1 = \frac{{169}}{{144}} - 1 = \frac{{25}}{{144}}\) \( \Rightarrow \tan \alpha = \pm \frac{5}{{12}}\) \( \Rightarrow \cot \alpha = \frac{1}{{\tan \alpha }} = \pm \frac{{12}}{5}\) Chọn B. Câu 2: \(\tan \alpha = \frac{{12}}{{35}}\)
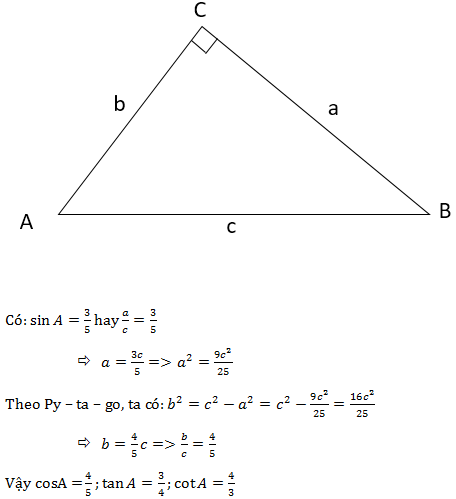
Đáp án: C Phương pháp giải: Sử dụng công thức lượng giác: \(\left\{ \begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\tan \alpha .\cot \alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\end{array} \right.\) Lời giải chi tiết: \(\tan \alpha = \frac{{12}}{{35}}\) Ta có: \(\tan \alpha .\cot \alpha = 1\)\( \Leftrightarrow \cot \alpha = \frac{1}{{\tan \alpha }} = 1:\frac{{12}}{{35}} = \frac{{35}}{{12}}\) Lại có: \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\)\( \Leftrightarrow 1 + {\left( {\frac{{12}}{{35}}} \right)^2} = \frac{1}{{{{\cos }^2}\alpha }}\)\( \Leftrightarrow \frac{1}{{{{\cos }^2}\alpha }} = \frac{{1369}}{{1225}}\)\( \Rightarrow {\cos ^2}\alpha = \frac{{1225}}{{1369}}\)\( \Rightarrow \cos \alpha = \pm \frac{{35}}{{37}}\) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)\( \Leftrightarrow {\left( {\frac{{35}}{{37}}} \right)^2} + {\sin ^2}\alpha = 1\)\( \Leftrightarrow {\sin ^2}\alpha = 1 - \frac{{1225}}{{1369}} = \frac{{144}}{{1369}}\)\( \Rightarrow \sin \alpha = \pm \frac{{12}}{{37}}\) Chọn C. Câu hỏi 6 : Tính các tỷ số lượng giác còn lại của \(\alpha \) biết: Câu 1: \({\rm{cos}}\alpha = \frac{3}{4}\)
Đáp án: A Phương pháp giải: Sử dụng công thức lượng giác: \(\left\{ \begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\tan \alpha .\cot \alpha = 1\\1 + {\cot ^2}\alpha = \frac{1}{{si{n^2}\alpha }}\end{array} \right..\) Lời giải chi tiết: \({\rm{cos}}\alpha = \frac{3}{4}\) *\({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)\( \Leftrightarrow {\sin ^2}\alpha + {\left( {\frac{3}{4}} \right)^2} = 1\)\( \Leftrightarrow {\sin ^2}\alpha = 1 - \frac{9}{{25}} = \frac{{16}}{{25}}\)\( \Rightarrow \sin \alpha = \pm \frac{4}{5}\) *\(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \pm \frac{4}{5}:\frac{3}{4} = \pm \frac{{16}}{{15}}\) *\(\cot \alpha = \frac{1}{{\tan \alpha }} = 1:\left( { \pm \frac{{16}}{{15}}} \right) = \pm \frac{{15}}{{16}}\) Chọn A. Câu 2: \(cot\alpha = \frac{8}{{15}}\)
Đáp án: D Phương pháp giải: Sử dụng công thức lượng giác: \(\left\{ \begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\tan \alpha .\cot \alpha = 1\\1 + {\cot ^2}\alpha = \frac{1}{{si{n^2}\alpha }}\end{array} \right..\) Lời giải chi tiết: \(cot\alpha = \frac{8}{{15}}\) * \(\tan \alpha .\cot \alpha = 1 \Leftrightarrow tan\alpha = \frac{1}{{\cot \alpha }} = \frac{1}{{\frac{8}{{15}}}} = \frac{{15}}{8}\) * \(1 + {\cot ^2}\alpha = \frac{1}{{si{n^2}\alpha }}\)\( \Leftrightarrow 1 + {\left( {\frac{8}{{15}}} \right)^2} = \frac{1}{{si{n^2}\alpha }}\)\( \Leftrightarrow \frac{1}{{si{n^2}\alpha }} = \frac{{289}}{{225}}\)\( \Rightarrow si{n^2}\alpha = \frac{{225}}{{289}}\)\( \Rightarrow sin\alpha = \pm \frac{{15}}{{17}}\) *\({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)\( \Leftrightarrow {\left( {\frac{{15}}{{17}}} \right)^2} + {\cos ^2}\alpha = 1\)\( \Leftrightarrow {\cos ^2}\alpha = 1 - \frac{{225}}{{289}} = \frac{{64}}{{289}}\)\( \Rightarrow \cos \alpha = \pm \frac{8}{{17}}\) Chọn D. Câu hỏi 7 : Giá trị của biểu thức \(P = {\cos ^2}{20^0} + {\cos ^2}{40^0} + {\cos ^2}{50^0} + {\cos ^2}{70^0}\) bằng
Đáp án: C Phương pháp giải: +) Sử dụng công thức: \(\sin \alpha = \cos \left( {{{90}^0} - \alpha } \right);\;\;{\sin ^2}\alpha + {\cos ^2}\alpha = 1.\) Lời giải chi tiết: Ta có: \(\begin{array}{l}P = {\cos ^2}{20^0} + {\cos ^2}{40^0} + {\cos ^2}{50^0} + {\cos ^2}{70^0}\\ = {\cos ^2}{20^0} + {\cos ^2}{40^0} + {\sin ^2}{40^0} + {\sin ^2}{20^0}\\ = \left( {{{\cos }^2}{{20}^0} + {{\sin }^2}{{20}^0}} \right) + \left( {{{\cos }^2}{{40}^0} + {{\sin }^2}{{40}^0}} \right)\\ = 1 + 1 = 2.\end{array}\) Chọn C. Câu hỏi 8 : Tính giá trị của các biểu thức sau: Câu 1: \(A = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\sin ^2}{55^0} + {\sin ^2}{65^0} + {\sin ^2}{75^0}\)
Đáp án: B Phương pháp giải: Sử dụng các công thức đặc biệt: \(\left\{ \begin{array}{l}\sin \alpha = \cos \left( {{{90}^0} - \alpha } \right)\\\tan \alpha = \cot \left( {{{90}^0} - \alpha } \right)\\{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\tan \alpha .\cot \alpha = 1\end{array} \right..\) Lời giải chi tiết: \(\,\,A = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\sin ^2}55 + {\sin ^2}{65^0} + {\sin ^2}{75^0}\) Ta có: \(\begin{array}{l}A = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\sin ^2}55 + {\sin ^2}{65^0} + {\sin ^2}{75^0}\\\,\,\,\,\, = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\cos ^2}{35^0} + {\cos ^2}{25^0} + {\cos ^2}{15^0}\\\,\,\,\,\, = \left( {{{\sin }^2}{{15}^0} + {{\cos }^2}{{15}^0}} \right) + \left( {{{\sin }^2}{{25}^0} + {{\cos }^2}25} \right) + \left( {{{\sin }^2}{{35}^0} + {{\cos }^2}{{35}^0}} \right) + {\sin ^2}{45^0}\\\,\,\,\, = 1 + 1 + 1 + {\left( {\frac{{\sqrt 2 }}{2}} \right)^2} = 3 + \frac{1}{2} = \frac{7}{2}.\end{array}\) Câu 2: \(B = \tan {10^0}.\tan {80^0} - \tan {20^0}.\tan {70^0}.\)
Đáp án: A Phương pháp giải: Sử dụng các công thức đặc biệt: \(\left\{ \begin{array}{l}\sin \alpha = \cos \left( {{{90}^0} - \alpha } \right)\\\tan \alpha = \cot \left( {{{90}^0} - \alpha } \right)\\{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\tan \alpha .\cot \alpha = 1\end{array} \right..\) Lời giải chi tiết: \(\,\,B = \tan {10^0}.\tan {80^0} - \tan {20^0}.\tan {70^0}.\) Ta có: \(\begin{array}{l}\,B = \tan {10^0}.\tan {80^0} - \tan {20^0}.\tan {70^0}\\\,\,\,\,\, = \tan {10^0}.cot{10^0} - \tan {20^0}.\cot {20^0}\\\,\,\,\,\, = 1 - 1 = 0.\end{array}\) Câu hỏi 9 : Biết \({0^0} < \alpha < {90^0}\). Giá trị bủa biểu thức \(\left[ {\sin \alpha + 3\,\cos \left( {{{90}^0} - \alpha } \right)} \right]:\left[ {\sin \alpha - 2\cos \left( {{{90}^0} - \alpha } \right)} \right]\) bằng:
Đáp án: A Phương pháp giải: Áp dụng tính chất: \(\sin \alpha = \cos \left( {{{90}^0} - \alpha } \right);\,\,\,\,\cos \alpha = \sin \left( {{{90}^0} - \alpha } \right).\) Lời giải chi tiết: \(\begin{array}{l}\left[ {\sin \alpha + 3\,\cos \left( {{{90}^0} - \alpha } \right)} \right]:\left[ {\sin \alpha - 2\cos \left( {{{90}^0} - \alpha } \right)} \right] = \left( {\sin \alpha + 3\sin \alpha } \right):\left( {\sin \alpha - 2\sin \alpha } \right)\\ = \left( {4\sin \alpha } \right):\left( { - \sin \alpha } \right) = - 4.\end{array}\) Chọn A Câu hỏi 10 : Tính số đo góc nhọn \(\alpha \) biết \(10{\sin ^2}\alpha + 6{\cos ^2}\alpha = 8\).
Đáp án: B Phương pháp giải: - Sử dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\,\,\forall \alpha \). - Tính \(\sin \alpha \), từ đo suy ra số đo góc \(\alpha \). Lời giải chi tiết: Ta có: \(10{\sin ^2}\alpha + 6{\cos ^2}\alpha = 8\) \(\begin{array}{l} \Leftrightarrow 4{\sin ^2}\alpha + 6\left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right) = 8\\ \Leftrightarrow 4{\sin ^2}\alpha + 6 = 8\\ \Leftrightarrow {\sin ^2}\alpha = \dfrac{1}{2} \Leftrightarrow \sin \alpha = \pm \dfrac{{\sqrt 2 }}{2}\end{array}\) \(Do\,\,\alpha < {90^0} \Rightarrow \sin \alpha > 0 \Leftrightarrow \sin \alpha = \dfrac{{\sqrt 2 }}{2}.\) Vậy \(\alpha = {45^0}.\) Chọn B. Câu hỏi 11 : Hãy đơn giản các biểu thức: Câu 1: \(1 - {\sin ^2}x\)
Đáp án: A Phương pháp giải: Sử dụng công thức lượng giác: \(\left\{ \begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\end{array} \right..\) Lời giải chi tiết: \(1 - {\sin ^2}x = {\cos ^2}x\) Chọn A. Câu 2: \(\sin x - \sin x.{\rm{co}}{{\rm{s}}^2}x\)
Đáp án: D Phương pháp giải: Sử dụng công thức lượng giác: \(\left\{ \begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\end{array} \right..\) Lời giải chi tiết: \(\sin x - \sin x.{\rm{co}}{{\rm{s}}^2}x\)\( = \sin x\left( {1 - {\rm{co}}{{\rm{s}}^2}x} \right)\)\( = \sin x.{\sin ^2}x = {\sin ^3}x\) Chọn D. Câu 3: \({\tan ^2}x - {\sin ^2}x.{\tan ^2}x\)
Đáp án: D Phương pháp giải: Sử dụng công thức lượng giác: \(\left\{ \begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\end{array} \right..\) Lời giải chi tiết: \({\tan ^2}x - {\sin ^2}x.{\tan ^2}x\)\( = {\tan ^2}x\left( {1 - {{\sin }^2}x} \right)\)\( = \frac{{{{\sin }^2}x}}{{co{s^2}x}}.co{s^2}x = {\sin ^2}x\) Chọn D. Câu hỏi 12 : Cho biểu thức \(A = \frac{{1 - 2\sin \alpha \cos \alpha }}{{{{\sin }^2}\alpha - {{\cos }^2}\alpha }}\) với \(\alpha \ne {45^0}\) a) Chứng minh rằng \(A = \frac{{\sin \alpha - \cos \alpha }}{{\sin \alpha + \cos \alpha }}\) b) Tính giá trị của A biết \(\tan \alpha = \frac{1}{3}\).
Đáp án: B Phương pháp giải: Sử dụng công thức lượng giác: \(\left\{ \begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\end{array} \right..\) Sử dụng hằng đẳng thức. Lời giải chi tiết: a) Chứng minh rằng \(A = \frac{{\sin \alpha - c{\rm{os}}\alpha }}{{\sin \alpha + c{\rm{os}}\alpha }}\) \(\begin{array}{l}A = \frac{{1 - 2\sin \alpha \cos \alpha }}{{{{\sin }^2}\alpha - c{\rm{o}}{{\rm{s}}^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha - 2\sin \alpha \cos \alpha }}{{\left( {\sin \alpha - \cos \alpha } \right)\left( {\sin \alpha + \cos \alpha } \right)}}\\ = \frac{{{{\left( {\sin \alpha - \cos \alpha } \right)}^2}}}{{\left( {\sin \alpha - \cos \alpha } \right)\left( {\sin \alpha + \cos \alpha } \right)}}\\ = \frac{{\sin \alpha - \cos \alpha }}{{\sin \alpha + \cos \alpha }}\,\,\,\,\,\left( {dpcm} \right).\end{array}\) b) Tính giá trị của A biết \(\tan \alpha = \frac{1}{3}\). Theo ý a ta có: \(A = \frac{{\sin \alpha - \cos \alpha }}{{\sin \alpha + \cos \alpha }} = \frac{{\tan \alpha - 1}}{{\tan \alpha + 1}}\) Thay \(\tan \alpha = \frac{1}{3}\) vào A ta được: \(A = \frac{{\tan \alpha - 1}}{{\tan \alpha + 1}} = \frac{{\frac{1}{3} - 1}}{{\frac{1}{3} + 1}} = - \frac{1}{2}\) Chọn B. Câu hỏi 13 : Tính giá trị của các biểu thức: Câu 1: \(A = \frac{{\cos {{41}^0}}}{{\sin {{49}^0}}} + \tan {28^0}.\tan {62^0}\)
Đáp án: B Phương pháp giải: Sử dụng các công thức lượng giác: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1;\)\(\,\tan \alpha .cot\alpha = 1.\) Cho \(\angle B + \angle C = {90^0}.\) Khi đó ta có: \(\left\{ \begin{array}{l}\sin B = \cos C\\\cos B = \sin C\end{array} \right..\) Lời giải chi tiết: \(A = \frac{{\cos {{41}^0}}}{{\sin {{49}^0}}} + \tan {28^0}.\tan {62^0}\) \(A = \frac{{\cos {{41}^0}}}{{\sin {{49}^0}}} + \tan {28^0}.\tan {62^0}\)\( = \frac{{\sin {{49}^0}}}{{\sin {{49}^0}}} + \tan {28^0}.cot{28^0}\)\( = 1 + 1 = 2.\) Chọn B. Câu 2: \(B = {\cos ^2}{10^0} + {\cos ^2}{20^0} + {\cos ^2}{70^0} + {\cos ^2}{80^0}\)
Đáp án: B Phương pháp giải: Sử dụng các công thức lượng giác: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1;\)\(\,\tan \alpha .cot\alpha = 1.\) Cho \(\angle B + \angle C = {90^0}.\) Khi đó ta có: \(\left\{ \begin{array}{l}\sin B = \cos C\\\cos B = \sin C\end{array} \right..\) Lời giải chi tiết: \(B = {\cos ^2}{10^0} + {\cos ^2}{20^0} + {\cos ^2}{70^0} + {\cos ^2}{80^0}\) \(\begin{array}{l}B = {\cos ^2}{10^0} + {\cos ^2}{20^0} + {\cos ^2}{70^0} + {\cos ^2}{80^0}\\ = {\cos ^2}{10^0} + {\cos ^2}{20^0} + si{n^2}{20^0} + si{n^2}{10^0}\\ = \left( {{{\cos }^2}{{20}^0} + si{n^2}{{20}^0}} \right) + \left( {{{\cos }^2}{{10}^0} + si{n^2}{{10}^0}} \right)\\ = 1 + 1 = 2.\end{array}\) Chọn B. Câu hỏi 14 : Tính giá trị của các biểu thức: Câu 1: \(C = {(3\sin \alpha + 4\cos \alpha )^2} + {\left( {4\sin \alpha - 3\cos \alpha } \right)^2}\)
Đáp án: D Phương pháp giải: Sử dụng công thức tỉ số lượng giác của góc nhọn. Sử dụng công thức lượng giác: \(\left\{ \begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\tan \alpha .\cot \alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\end{array} \right..\) Lời giải chi tiết: \(C = {(3\sin \alpha + 4\cos \alpha )^2} + {\left( {4\sin \alpha - 3\cos \alpha } \right)^2}\) \(\begin{array}{l}C = {\left( {3\sin \alpha + 4\cos \alpha } \right)^2} + {\left( {4\sin \alpha - 3\cos \alpha } \right)^2}\\ = 9{\sin ^2}\alpha + 24\sin \alpha \cos \alpha + 16{\cos ^2}\alpha + 16{\sin ^2}\alpha - 24\sin \alpha \cos \alpha + 9{\cos ^2}\alpha \\ = 25{\sin ^2}\alpha + 25{\cos ^2}\alpha \\ = 25\left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right) = 25.\end{array}\) Chọn D. Câu 2: Cho biết \(\tan \alpha = \frac{2}{3}\). Tính giá trị biểu thức: \(M = \frac{{{{\sin }^3}\alpha + 3{{\cos }^3}\alpha }}{{27{{\sin }^3}\alpha - 25{{\cos }^3}\alpha }}\)
Đáp án: C Phương pháp giải: Sử dụng công thức tỉ số lượng giác của góc nhọn. Sử dụng công thức lượng giác: \(\left\{ \begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\tan \alpha .\cot \alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\end{array} \right..\) Lời giải chi tiết: \(M = \frac{{{{\sin }^3}\alpha + 3{{\cos }^3}\alpha }}{{27{{\sin }^3}\alpha - 25{{\cos }^3}\alpha }} = \frac{{\frac{{{{\sin }^3}\alpha }}{{{{\cos }^3}\alpha }} + 3}}{{\frac{{27{{\sin }^3}\alpha }}{{{{\cos }^3}\alpha }} - 25}} = \frac{{{{\tan }^3}\alpha + 3}}{{27{{\tan }^3}\alpha - 25}}\) Thay \(\tan \alpha = \frac{2}{3}\) vào biểu thức \(M\) ta có: \(M = \frac{{{{\tan }^3}\alpha + 3}}{{27{{\tan }^3}\alpha - 25}} = \frac{{{{\left( {\frac{2}{3}} \right)}^3} + 3}}{{27{{\left( {\frac{2}{3}} \right)}^3} - 25}} = - \frac{{89}}{{459}}.\) Chọn C. Câu hỏi 15 : Tính giá trị biểu thức: Câu 1: \(M = {\sin ^2}{42^o} + {\sin ^2}{43^o} + {\sin ^2}{44^o} + {\sin ^2}{45^o} + {\sin ^2}{46^o} + {\sin ^2}{47^o} + {\sin ^2}{48^o}\)
Đáp án: D Phương pháp giải: Sử dụng tính chất hai góc phụ nhau: \(\alpha + \beta = {90^0} \Rightarrow \left\{ \begin{array}{l}\sin \alpha = \cos \beta \\\cos \alpha = \sin \beta \end{array} \right.\) Sử dụng công thức lượng giác: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) Giá trị lượng giác của một số góc đặc biệt. Lời giải chi tiết: \(M = {\sin ^2}{42^o} + {\sin ^2}{43^o} + {\sin ^2}{44^o} + {\sin ^2}{45^o} + {\sin ^2}{46^o} + {\sin ^2}{47^o} + {\sin ^2}{48^o}\) \(\begin{array}{l}M = {\sin ^2}{42^o} + {\sin ^2}{43^o} + {\sin ^2}{44^o} + {\sin ^2}{45^o} + {\sin ^2}{46^o} + {\sin ^2}{47^o} + {\sin ^2}{48^o}\\ = {\sin ^2}{42^o} + {\sin ^2}{43^o} + {\sin ^2}{44^o} + {\sin ^2}{45^o} + {\cos ^2}{44^o} + {\cos ^2}{43^o} + {\cos ^2}{42^o}\\ = \left( {{\rm{si}}{{\rm{n}}^2}{{42}^o} + {\rm{co}}{{\rm{s}}^2}{{42}^o}} \right) + \left( {{{\sin }^2}{{43}^o}{\rm{ + co}}{{\rm{s}}^2}{{43}^o}} \right) + \left( {{\rm{ }}{{\sin }^2}{{44}^o} + {\rm{co}}{{\rm{s}}^2}{{44}^o}} \right) + {\sin ^2}{45^o}\\ = 1 + 1 + 1 + \frac{1}{2} = \frac{7}{2}\end{array}\) Chọn D. Câu 2: \(N = {\cos ^2}{15^o} - {\cos ^2}{25^o} + {\cos ^2}{35^o} - {\cos ^2}{45^o} + {\cos ^2}{55^o} - {\cos ^2}{65^o} + {\cos ^2}{75^o}\)
Đáp án: A Phương pháp giải: Sử dụng tính chất hai góc phụ nhau: \(\alpha + \beta = {90^0} \Rightarrow \left\{ \begin{array}{l}\sin \alpha = \cos \beta \\\cos \alpha = \sin \beta \end{array} \right.\) Sử dụng công thức lượng giác: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) Giá trị lượng giác của một số góc đặc biệt. Lời giải chi tiết: \(N = {\cos ^2}{15^o} - {\cos ^2}{25^o} + {\cos ^2}{35^o} - {\cos ^2}{45^o} + {\cos ^2}{55^o} - {\cos ^2}{65^o} + {\cos ^2}{75^o}\) \(\begin{array}{l}N = {\cos ^2}{15^o} - {\cos ^2}{25^o} + {\cos ^2}{35^o} - {\cos ^2}{45^o} + {\cos ^2}{55^o} - {\cos ^2}{65^o} + {\cos ^2}{75^o}\\ = {\cos ^2}{15^o} - {\cos ^2}{25^o} + {\cos ^2}{35^o} - {\cos ^2}{45^o} + {\sin ^2}{35^o} - {\sin ^2}{25^o} + {\sin ^2}{15^0}\\ = \left( {{{\cos }^2}{{15}^o} + si{n^2}{{15}^0}} \right) - \left( {{{\cos }^2}{{25}^o} + si{n^2}{{25}^0}} \right) + \left( {{{\cos }^2}{{35}^o} + si{n^2}{{35}^0}} \right) - {\cos ^2}{45^o}\\ = 1 - 1 + 1 - \frac{1}{2} = \frac{1}{2}\end{array}\) Chọn A. Câu hỏi 17 :
Đáp án: B Phương pháp giải: Lời giải chi tiết:
Câu hỏi 19 : a) \(1 + {\rm{ }}{\tan ^2}x{\rm{ }} = \frac{1}{{{{\cos }^2}x}}\) b) \(1 + {\cot ^2}x = \frac{1}{{{{\sin }^2}x}}\) c) \({\cos ^4}x-{\rm{ si}}{{\rm{n}}^4}x = 2{\cos ^2}x{\rm{ }} - 1\) d) \({\sin ^6}x + {\cos ^6}x{\rm{ }} = {\rm{ }}1 - {\rm{ }}3{\sin ^2}x.{\cos ^2}x\) Phương pháp giải: Sử dụng công thức lượng giác: \(\left\{ \begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\\\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\end{array} \right..\) Sử dụng hằng đẳng thức. Lời giải chi tiết: a) \(1 + {\rm{ }}{\tan ^2}x{\rm{ }} = \frac{1}{{{{\cos }^2}x}}\) \(VT = 1 + {\rm{ }}{\tan ^2}x\)\( = 1 + \frac{{{{\sin }^2}x}}{{{{\cos }^2}x}}\)\( = \frac{{{{\cos }^2}x + {{\sin }^2}x}}{{{{\cos }^2}x}}\)\( = \frac{1}{{{{\cos }^2}x}} = VP\)(đpcm) b) \(1 + {\cot ^2}x{\rm{ }} = \frac{1}{{{{\sin }^2}x}}\) \(VT = 1 + {\cot ^2}x{\rm{ }} = 1 + \frac{{{{\cos }^2}x}}{{{{\sin }^2}x}}\)\( = \frac{{{{\sin }^2}x + {{\cos }^2}x}}{{{{\sin }^2}x}} = \frac{1}{{{{\sin }^2}x}}\) (đpcm) c) \({\cos ^4}x--{\sin ^4}x = 2{\cos ^2}x{\rm{ }} - 1\) \(\begin{array}{l}{\cos ^4}x--{\sin ^4}x = \left( {{{\cos }^2}x--{{\sin }^2}x} \right)\left( {{{\cos }^2}x{\rm{ + }}{{\sin }^2}x} \right)\\ = {\cos ^2}x--{\sin ^2}x = {\cos ^2}x - \left( {1 - {{\cos }^2}x{\rm{ }}} \right)\\ = 2{\cos ^2}x{\rm{ }} - 1\,\,\,\,\left( {dpcm} \right)\end{array}\) d. \({\sin ^6}x + {\cos ^6}x{\rm{ }} = 1 - 3{\sin ^2}x.{\cos ^2}x\) \(\begin{array}{l}{\sin ^6}x + {\cos ^6}x = \left( {{{\sin }^2}x + {{\cos }^2}x} \right)\left( {{{\sin }^4}x - {{\sin }^2}x.{{\cos }^2}x + {{\cos }^4}x} \right)\\ = \left( {{{\sin }^4}x + {{\cos }^4}x} \right) - {\sin ^2}x.{\cos ^2}x\\ = {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^2} - 2{\sin ^2}x.{\cos ^2}x - {\sin ^2}x.{\cos ^2}x\\ = 1 - 3{\sin ^2}x.{\cos ^2}x\,\,\,\,\left( {dpcm} \right)\end{array}\) Câu hỏi 20 : Chứng minh rằng giá trị của các biểu thức sau không phụ thuộc vào giá trị của góc nhọn \(\alpha \). a) \({\left( {\cos \alpha - \sin \alpha } \right)^2} + {\left( {\cos \alpha + \sin \alpha } \right)^2}\) b) \(\frac{{{{(c{\rm{os}}\alpha - \sin \alpha )}^2} - {{(c{\rm{os}}\alpha + \sin \alpha )}^2}}}{{c{\rm{os}}\alpha .\sin \alpha }}\) Phương pháp giải: Sử dụng công thức lượng giác: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) Sử dụng hằng đẳng thức. Lời giải chi tiết: a) \({\left( {\cos \alpha - {\rm{sin}}\alpha } \right)^2} + {\left( {\cos \alpha - {\rm{sin}}\alpha } \right)^2}\) \(\begin{array}{l}{\left( {\cos \alpha - {\rm{sin}}\alpha } \right)^2} + {\left( {\cos \alpha + {\rm{sin}}\alpha } \right)^2}\\ = {\cos ^2}\alpha - 2{\rm{sin}}\alpha .\cos \alpha + {\rm{si}}{{\rm{n}}^2}\alpha + {\cos ^2}\alpha + 2{\rm{sin}}\alpha \cos \alpha + {\rm{si}}{{\rm{n}}^2}\alpha \\ = 2{\rm{si}}{{\rm{n}}^2}\alpha + 2{\cos ^2}\alpha = 2\left( {{\rm{si}}{{\rm{n}}^2}\alpha + {{\cos }^2}\alpha } \right) = 2.1 = 2.\end{array}\) Vậy giá trị của các biểu thức trên không phụ thuộc vào giá trị của góc nhọn \(\alpha \). b. \(\frac{{{{\left( {\cos \alpha - \sin \alpha } \right)}^2} - {{\left( {\cos \alpha + \sin \alpha } \right)}^2}}}{{\cos \alpha .\sin \alpha }}\) \(\begin{array}{l}\frac{{{{\left( {\cos \alpha - \sin \alpha } \right)}^2} - {{\left( {\cos \alpha + \sin \alpha } \right)}^2}}}{{\cos \alpha .\sin \alpha }}\\ = \frac{{{{\cos }^2}\alpha - 2\sin \alpha .\cos \alpha + {{\sin }^2}\alpha - {{\cos }^2}\alpha - 2\sin \alpha \cos \alpha - {{\sin }^2}\alpha }}{{\cos \alpha .\sin \alpha }}\\ = \frac{{ - 4\sin \alpha \cos \alpha }}{{\cos \alpha .\sin \alpha }} = - 4.\end{array}\) Vậy giá trị của các biểu thức trên không phụ thuộc vào giá trị của góc nhọn \(\alpha \). Quảng cáo
|