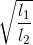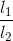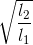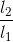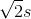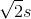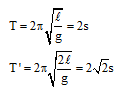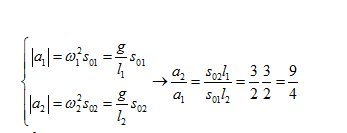40 bài tập con lắc đơn mức độ thông hiểuLàm bàiQuảng cáo
Câu hỏi 1 : Một con lắc đơn dao động điều hòa theo phương trình \(s = 2\cos \left( {\pi t + {\pi \over 3}} \right)\) cm.Tần số dao động của con lắc đơn này là
Đáp án: A Phương pháp giải: Lời giải chi tiết: Tần số dao dộng của con lắc là \(f = {\omega \over {2\pi }} = {\pi \over {2\pi }} = 0,5Hz\) Câu hỏi 2 : Con lắc đơn có chiều dài dây treo l = 0.25m thực hiện 10 dao động mất 10s. Lấy π = 3,14. Gia tốc trọng trường tại nơi đặt con lắc là:
Đáp án: B Phương pháp giải: Sử dụng công thức tính chu kì của con lắc đơn \(T = 2\pi \sqrt {\frac{l}{g}} \) Chu kì của dao động điều hoà là khoảng thời gian để vật thực hiện được một dao động toàn phần Lời giải chi tiết: Con lắc thực hiện 10 dao động hết 10 s → Chu kì dao động T = 1s Ta có: \(T = 2\pi \sqrt {\frac{l}{g}} \Rightarrow g = \frac{{4{\pi ^2}l}}{{{T^2}}} = \frac{{{{4.3,14}^2}.0,25}}{1} = 9,86\) m/s2 Câu hỏi 3 : Tại một nơi xác định, hai con lắc đơn có độ dài l1 và l2, dao động điều hoà với tần số tương ứng f1 và f2. Tỉ số f1/f2 bằng
Đáp án: C Phương pháp giải: Phương pháp : Sử dụng công thức tính tần số của con lắc đơn dao động điều hoà Lời giải chi tiết: Áp dụng công thức: $$f = {1 \over {2\pi }}\sqrt {{g \over \ell }} \Rightarrow {{{f_1}} \over {{f_2}}} = \sqrt {{{{l_2}} \over {{l_1}}}} $$ => Chọn C Câu hỏi 4 : Một con lắc đơn có phương trình động năng như sau: Wđ = 1 +1cos(10πt + π/3)(J). Hãy xác định tần số của dao động
Đáp án: C Phương pháp giải: Động năng biến thiên tuần hoàn với tần số góc bằng 2 lần tần số góc của vật dao động điều hoà Lời giải chi tiết: PT động năng: Wđ = 1 +1cos(10πt + π/3)(J) → Động năng biến thiên tuần hoàn theo thời gian với tần số góc: ω’ = 10π (rad/s) Do đó tần số góc của dao động là: ω = ω’/2 = 5π rad/s → Tần số của dao động: f = ω/2π = 2,5 Hz => Chọn C Câu hỏi 5 : Một con lắc đơn có chu kì dao động T= 2s tại nơi có g = 10 m/s2. Biên độ góc của dao động là 60. Vận tốc của con lắc tại vị trí có li độ góc 30 có độ lớn là
Đáp án: D Phương pháp giải: Áp dụng công thức tính vận tốc của con lắc đơn dao động điều hòa Lời giải chi tiết: Ta có: \(v = \sqrt {2gl\left( {\cos \alpha - \cos {\alpha _0}} \right)} = \sqrt {{{{T^2}g} \over {4{\pi ^2}}}.2g\left( {\cos \alpha - \cos {\alpha _0}} \right)} = {{Tg} \over {2\pi }}\sqrt {2\left( {\cos \alpha - \cos {\alpha _0}} \right)} = 0,287m/s\) Câu hỏi 6 : Một con lắc đơn dao động điều hòa tại nơi có gia tốc trọng trường g = 9,8 m/s2 với chu kì T = 2 s. Quả cầu nhỏ của con lắc có khối lượng m = 50 g. Biết biên độ góc α0 = 0,15 rad. Lấy π = 3,1416. Cơ năng dao động của con lắc bằng
Đáp án: D Phương pháp giải: Áp dụng công thức tính năng lượng dao động của con lắc đơn Lời giải chi tiết: + Chiều dài của con lắc đơn: \(l = \frac{{{T^2}g}}{{4{\pi ^2}}} = \frac{{{2^2}.9,8}}{{4{\pi ^2}}} = 0,993(m)\) + Cơ năng dao động của con lắc đơn: \(W = \frac{1}{2}mgl\alpha _0^2 = \frac{1}{2}{.0,05.9,8.0.993.0,15^2} \approx {5,5.10^{ - 3}} = {0,55.10^{ - 2}}(J)\) => Chọn D
Câu hỏi 7 : Một con lắc đơn chu kỳ T = 2s tại nơi có gia tốc rơi tự do là g = 10m/s2 và lấy π2 = 10. Chiều dài dây treo con lắc là:
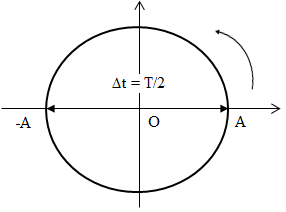
Đáp án: B Phương pháp giải: Áp dụng công thức tính chu kì dao động của con lắc đơn \(T = 2\pi \sqrt {{l \over g}} \) Lời giải chi tiết: Chiều dài của con lắc đơn: \(l = {{{T^2}g} \over {4{\pi ^2}}} = {{{2^2}.10} \over {4.10}} = 1(m)\) Câu hỏi 8 : Một con lắc đơn dao động với biên độ nhỏ. Khoảng thời gian giữa hai lần liên tiếp vật nặng ở vị trí cao nhất là 1s. Chu kì dao động của con lắc là
Đáp án: A Phương pháp giải: Sử dụng vòng tròn lượng giác để xác định khoảng thời gian Lời giải chi tiết: Khoảng thời gian giữa hai lần liên tiếp vật nặng ở vị trí cao nhất, tức là vị trí biên là 1s => T/2 = 1 s => Chu kì dao động T = 2 s => Chọn A Câu hỏi 9 : Một con lắc đơn gồm quả cầu nhỏ khối lượng m được treo vào một đầu sợi dây mềm, nhẹ, không dãn, dài 64cm. Con lắc dao động điều hòa tại nơi có gia tốc trọng trường g. Lấy g = π2 (m/s2). Chu kì dao động của con lắc là :
Đáp án: B Phương pháp giải: Phương pháp: Áp dụng công thức tính chu kì dao động của con lắc đơn Lời giải chi tiết: Đáp án B Chu kì dao động: \(T = 2\pi \sqrt {{\ell \over g}} = 2\pi \sqrt {{{0,64} \over {{\pi ^2}}}} = 1,6{\rm{s}}\) Câu hỏi 10 : Tại cùng một nơi trên Trái Đất, con lắc đơn có chiều dài l dao động điều hòa với chu kì 2 s, con lắc đơn có chiều dài 2l dao động điều hòa với chu kì:
Đáp án: B Phương pháp giải: Phương pháp: Sử dụng công thức tính chu kì của con lắc đơn Lời giải chi tiết: Đáp án B Câu hỏi 11 : Con lắc đơn dao động điều hòa với phương trình \(s = \cos \left( {2t + 0,69} \right)\,\,cm\), t tính theo đơn vị giây. Khi t = 0,135s thì pha dao động là
Đáp án: C Phương pháp giải: Phương pháp: Thay t vào pha dao động Lời giải chi tiết: Đáp án C Pha dao động là (2.0,135+0,69)= 0,96rad Câu hỏi 12 : Một con lắc dao động điều hòa xung quanh vị trí cân bằng với chu kì T. Nếu gia tốc trọng trường giảm đi 4,5 lần, chiều dài dây treo giảm đi 2 lần thì chu kì dao động điều hòa của con lắc đơn thay đổi:
Đáp án: B Phương pháp giải: Áp dụng công thức tính chu kì dao động của con lắc đơn \(T = 2\pi \sqrt {{l \over g}} \) Lời giải chi tiết: Khi gia tốc trọng trường giảm 4,5 lần, chiều dài dây treo giảm 2 lần thì : \(T' = 2\pi \sqrt {{{{l \over 2}} \over {{g \over {4,5}}}}} = 2\pi \sqrt {{{4,5l} \over {2g}}} = 2\pi \sqrt {{l \over g}} .\sqrt {{9 \over 4}} = {3 \over 2}T\) Vậy chu kì tăng lên 1,5 lần Câu hỏi 13 : Con lắc đơn gồm vật nhỏ khối lượng m = 500 g, chiều dài dây treo là l, dao động điều hòa tại nơi có gia tốc trọng trường g = 10 m/s2 với góc lệch cực đại là α0 = 60. Giá trị lực căng dây treo khi con lắc đi qua vị trí vật có động năng bằng ba lần thế năng là
Đáp án: D Phương pháp giải: Công thức tính lực căng dây của treo trong dao động cơ của con lắc đơn T = mg(3cosα – 2cosα0) Lời giải chi tiết: Đáp án D Trả lời: + Vị trí động năng bằng 3 lần thế năng α = ± 0,5α0 = 30 Lực căng dây T = mg(3cosα – 2cosα0) = 5,034 N. Câu hỏi 14 : Lực phục hồi để tạo ra dao động của con lắc đơn là
Đáp án: B Phương pháp giải: Vận dụng lý thuyết tổng hợp lực Lời giải chi tiết: Lực phục hồi là tổng hợp của trọng lực và lực căng dây tác dụng lên con lắc đơn. Chọn B Câu hỏi 15 : Tại nơi có gia tốc trọng trường là 9,8 m/s2, một con lắc đơn dao động điều hòa với biên độ góc 60. Biết khối lượng vật nhỏ của con lắc dao động là 90 g và chiều dài dây treo là 1 m. Năng lượng dao động của vật là
Đáp án: D Phương pháp giải: Áp dụng công thức tính cơ năng của con lắc đơn với biên độ góc nhỏ Lời giải chi tiết: Cơ năng: \(E = {1 \over 2}mgl\alpha _0^2 = {1 \over 2}.0,09.1.{\left( {{{6\pi } \over {180}}} \right)^2} = {4,8.10^{ - 3}}J\) Chọn D Câu hỏi 16 : Xét dao động điều hòa của con lắc đơn tại một điểm trên mặt đất. Khi con lắc đơn đi từ vị trí biên về vị trí cân bằng thì
Đáp án: C Phương pháp giải: Vận dụng lí thuyết về dao động điều hòa Lời giải chi tiết: Đáp án C Ta có: + Độ lớn lực hồi phục: $${F_{hp}} = \left| { - kx} \right|$$ +Thế năng : $${W_t} = {{mgl{\alpha ^2}} \over 2}$$ - Khi con lắc ở vị trí biên: $$\alpha = {\alpha _0},v = 0$$ - Khi con lắc ở vị trí cân bằng: $$\alpha = 0,v = {v_{\max }}$$ Khi con lắc đơn từ vị trí biên về vị trí cân bằng thì: + Độ lớn li độ tăng + Tốc độ tăng + Độ lớn lực hồi phục giảm + Thế năng giảm Câu hỏi 17 : Một con lắc đơn dao động điều hòa tại nơi có g = 9,8 m/s2. Biết khối lượng của quả nặng m = 500 g, sức căng dây treo khi con lắc ở vị trí biên là 1,96 N. Lực căng dây treo khi con lắc đi qua vị trí cân bằng là:
Đáp án: B Phương pháp giải: Sử dụng công thức tính lực căng T. Lời giải chi tiết: Đáp án B Lực căng T tại vị trí bất kì: $$T = mg(3\cos \alpha - 2\cos {\alpha _0})$$ Tại vị trí biên là: $${T_{bien}} = mg\cos {\alpha _0} = 1,96N$$ Tại vị trí cân bằng: $${T_{cb}} = mg(3 - 2\cos {\alpha _0})$$ =>$${T_{cb}} = 3mg - 2mg\cos {\alpha _0} = 3.0,5.9,8 - 2.1,98 = 10,78N$$ Câu hỏi 18 : Một con lắc đơn dao động điều hòa với biên độ góc a0 = 50. Với li độ góc a bằng bao nhiêu thì động năng của con lắc gấp 2 lần thế năng?
Đáp án: C Phương pháp giải: Phương pháp : định luật bảo toàn cơ năng Lời giải chi tiết: Đáp án C + Ta có $$\left\{ \matrix{ {E_d} = 2{E_t} \hfill \cr {E_d} + {E_t} = E \hfill \cr} \right. \Rightarrow 3{E_t} = E \Rightarrow \alpha = \pm {{{\alpha _0}} \over {\sqrt 3 }} = \pm {2.89^0}$$ . Câu hỏi 19 : Một con lắc đơn có chiều dài dây treo l = 1 m, lấy g = 9,8 = π2 m/s2. Số lần động năng bằng thế năng trong khoảng thời gian 4 s là
Đáp án: D Phương pháp giải: Phương pháp: Áp dụng công thức tính chu kỳ của con lắc đơn $$T = 2\pi \sqrt {{l \over g}} $$ Lời giải chi tiết: Đáp án D + Chu kì dao động của con lắc đơn $$T = 2\pi \sqrt {{l \over g}}=2s $$ Mỗi chu kì động năng bằng thế năng 4 lần → với khoảng thời gian Δt = 2T = 4 s → động năng bằng thế năng 8 lần. Câu hỏi 20 : Một con lắc đơn dài l = 120 cm. Người ta thay đổi độ dài của nó sao cho chu kì dao động mới chỉ bằng 90% chu kì dao động ban đầu. Tính độ dài mới l’?
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D + Ta có $$T \sim \sqrt l \Rightarrow {\left( {{{T'} \over T}} \right)^2} = {{l'} \over l} \Rightarrow l = 0,{9^2}l = 97,2 cm $$. Câu hỏi 21 : Hai con lắc dơn có chu kì T1 = 2,0 s và T2 = 3,0 s. Tính chu kì con lắc đơn có độ dài bằng tổng chiều dài hai con lắc nói trên?
Đáp án: B Phương pháp giải: Lời giải chi tiết: Đáp án B + Ta có $$T \sim \sqrt l \buildrel {l = {l_1} + {l_2}} \over \longrightarrow T = \sqrt {T_1^2 + T_2^2} = 3,6 s $$ Câu hỏi 22 : Ở một nơi trên Trái Đất, hai con lắc đơn có cùng khối lượng đang dao động điều hòa. Gọi l1, s01, a1 và l2, s02, a2 lần lượt là chiều dài, biên độ, gia tốc dao động điều hòa cực đại theo phương tiếp tuyến của con lắc đơn thứ nhất và con lắc đơn thứ hai. Biết 3l2 =2l1, 2s02 =3s01. Tỉ số \({{{a_2}} \over {{a_1}}}\) bằng:
Đáp án: A Phương pháp giải: Sử dụng lí thuyết về các đại lượng trong dao động điều hòa của con lắc đơn. Lời giải chi tiết: Đáp án A Ta có: Câu hỏi 23 : Một con lắc đơn gồm một hòn bi nhỏ khối lượng m, treo vào một sợi dây không giãn, khối lượng sợi dây không đáng kể. Khi con lắc đơn này dao động với chu kỳ 3s thì hòn bi chuyển động trên một cung tròn dài 4 cm. Thời gian để hòn bi đi được 2 cm kể từ VTCB là
Đáp án: B Phương pháp giải: Lời giải chi tiết: Đáp án B + Thời gian tương ứng $$t = {T \over 2} = 0,25\,s$$ Câu hỏi 24 : Nếu giảm chiều dài của một con lắc đơn một đoạn 19 cm thì chu kì dao động nhỏ của nó thay đổi một lượng 0,2 s. Lấy g = π2 (m/s2). Chu kì dao động của con lắc ban đầu là
Đáp án: D Phương pháp giải: Sử dụng công thức tính chu kì dao động của con lắc đơn \(T = 2\pi \sqrt {{l \over g}} \) Lời giải chi tiết: Gọi chiều dài của con lắc đơn là l Ban đầu chu kì dao động của con lắc \(T = 2\pi \sqrt {{l \over g}} \) Sau khi giảm chiều dài của con lắc đi 19cm thì chu kì của con lắc là \(T' = 2\pi \sqrt {{{l - 0,19} \over g}} < T\) Theo đề bài ta có \(T' - T = 0,2 \Leftrightarrow 2\pi \sqrt {{l \over g}} - 2\pi \sqrt {{{l - 0,19} \over g}} = 0,2 \Leftrightarrow l = 1m\) Như vậy chu kì dao động ban đầu của con lắc là \(T = 2\pi \sqrt {{l \over g}} = 2\pi \sqrt {{{0,2} \over {{\pi ^2}}}} = 2s\) Câu hỏi 25 : Tại nơi có gia tốc trọng trường g, một con lắc đơn dao động điều hòa với biên độ góc α0. Biết khối lượng vật nhỏ của con lắc là m. Khi con lắc ở vị trí có li độ góc α thì lực căng dây là
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D Câu hỏi 26 : Một con lắc đơn có chiều dài 56 cm dao động điều hòa tại nơi có gia tốc rơi tự do g=9,8m/s2. Chu kì dao động của con lắc
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D Chu kỳ dao động của con lắc được xác định bởi biểu thức $$T = 2\pi \sqrt {{l \over g}} = 1,5s$$ Câu hỏi 27 : Khi cho chiều dài của một con lắc đơn tăng lên 4 lần thì chu kì dao động nhỏ của con lắc
Đáp án: B Phương pháp giải: Phương pháp: Áp dụng công thức tính chu kỳ của con lắc đơn
Lời giải chi tiết: Đáp án B $$T = 2\pi \sqrt {{l \over g}} ;T' = 2\pi \sqrt {{{4l} \over g}} = > {{T'} \over T} = 2$$ Câu hỏi 28 : Tại một nơi, chu kì dao động điều hoà của một con lắc đơn là 2,0 s. Sau khi tăng chiều dài của con lắc thêm 21 cm thì chu kì dao động điều hoà của nó là 2,2 s. Chiều dài ban đầu của con lắc này là
Đáp án: D Phương pháp giải: Phương pháp: Áp dụng công thức tính chu kỳ của con lắc đơn Lời giải chi tiết: Đáp án D \({{T'} \over T} = \sqrt {{{l + 21} \over l}} = > {{2,2} \over 2} = \sqrt {{{l + 21} \over l}} = > l = 100cm\) Câu hỏi 29 : Một con lắc đơn dài l = 1,6m dao động điều hòa với biên độ 16cm. Lấy π = 3,14. Biên độ góc của dao động gần giá trị nào nhất sau đây?
Đáp án: A Phương pháp giải: Lời giải chi tiết: Đáp án A + Biên độ góc của dao động \({\alpha _0} = {{{s_0}} \over l} = 0,1\,\,ra{\rm{d}} = 5,{73^0}\) Câu hỏi 30 : Trong một dao động toàn phần của một con lắc đơn đang dao động điều hòa, số lần thế năng của con lắc đạt giá trị cực đại là
Đáp án: B Phương pháp giải: Lời giải chi tiết: Đáp án B + Thế năng của con lắc đạt cực đại tại vị trí biên → trong một chu kì thế năng cực đại hai lần. Câu hỏi 31 : Một con lắc đơn có chiều dài L = 0,5m; vật nhỏ có khối lượng m = 200g. Từ vị trí cân bằng đưa vật đến vị trí mà dây treo lệch một góc 300 theo phương thẳng đứng rồi thả nhẹ vật. Bỏ qua mọi ma sát, lấy g = 10 m/s2. Tính động năng của vật khi vật đi qua vị trí cân bằng:
Đáp án: C Phương pháp giải: Động năng Wđ = mv2/2 Vận tốc: \(v = \sqrt {2gl(c{\rm{os}}\alpha - c{\rm{os}}{\alpha _0})} \) Lời giải chi tiết: Ở VTCB:\(v = \sqrt {2gl(1 - c{\rm{os}}{\alpha _0})} \Rightarrow {{\rm{W}}_d} = {1 \over 2}m{v^2} = {1 \over 2}.m.2gl(1 - c{\rm{os}}{\alpha _0}) = 0,2.10.0,5.(1 - c{\rm{os30) = 0,134J}}\) Chọn C Câu hỏi 32 : Một con lắc đơn có khối lượng vật nặng là m dao động điều hòa với tần số f. Nếu tăng khối lượng vật nặng thành 2m thì khi đó tần số dao động của con lắc là
Đáp án: A Phương pháp giải: Sử dụng công thức tính tần số dao động của con lắc đơn: \(f = {1 \over {2\pi }}\sqrt {{g \over l}} \) Lời giải chi tiết: Tần số dao động của con lắc đơn không phụ thuộc vào khối lượng của vật nặng => khi thay đổi khối lượng vật nặng thì f không thay đổi. Câu hỏi 33 : Tại nơi có gia tốc trọng trường là 9,8 m/s2, một con lắc đơn dao động điều hòa với biên độ góc 60. Biết khối lượng vật nhỏ của con lắc là 90 g và chiều dài dây treo là 1 m. Chọn mốc thế năng tại vị trí cân bằng, cơ năng của con lắc xấp xỉ bằng
Đáp án: D Phương pháp giải: Cơ năng của con lắc đơn dao động điều hoà: \({\rm{W}} = {{mgl\alpha _0^2} \over 2}\) (đơn vị của α0 là rad) Lời giải chi tiết: Ta có: \({\alpha _0} = {6^0} = 6.{\pi \over {180}}{\rm{ = }}0,1047{\rm{ }}rad\). Cơ năng của con lắc: \({\rm{W}} = {{mgl\alpha _0^2} \over 2} = {{{{90.10}^{ - 3}}{{.9,8.1.0,1047}^2}} \over 2} = {4,8.10^{ - 3}}J\) Câu hỏi 34 : Một con lắc đơn có dây treo dài l , vật nặng khối lượng m đặt tại nơi có gia tốc trọng trường g, biên độ góc là \({\alpha _0} < 10^\circ \) . Chọn mốc thế năng là vị trí thấp nhất của vật. Khi con lắc đi qua vị trí có li độ góc thì thế năng của vật nặng là
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án D + Thế năng của vật nặng tại vị trí có li độ góc \(\alpha \) được xác định bởi biểu thức \({E_t} = 0,5mgl{\alpha ^2}\). Câu hỏi 35 : Trong thí nghiệm khảo sát dao động điều hòa về con lắc đơn, khi thay quả nặng 50 (g) bằng quả nặng 20 (g) thì
Đáp án: B Phương pháp giải: tần số dao động của con lắc đơn Lời giải chi tiết: Vì tần số dao động của con lắc đơn là:
không phụ thuộc vào khối lượng nên dù thay quả nặng khác thì tần số (chu kì) của dao động không đổi. Câu hỏi 36 : Hai con lắc đơn treo vật cùng khối lượng, dao động điều hòa cùng cơ năng với biên độ dao động lần lượt là A1, A2. Biểu thức đúng về mối liên hệ giữa biên độ dao động và chiều dài dây là
Đáp án: A Phương pháp giải: Áp dụng công thức tính cơ năng của con lắc đơn W = 0,5mglα02 . Lời giải chi tiết: Ta có \({{\rm{W}}_1} = {{\rm{W}}_2} \Leftrightarrow {1 \over 2}mg{\ell _1}A_1^2 = {1 \over 2}mg{\ell _2}A_2^2 \Leftrightarrow {\ell _1}A_1^2 = {\ell _2}A_2^2 \Rightarrow {A_2} = {A_1}\sqrt {{{{\ell _1}} \over {{\ell _2}}}} \) Chọn đáp án A Câu hỏi 37 : Một con lắc đơn dây treo có chiều dài là ℓ làm bằng kim loại, được treo tại một nơi có gia tốc trọng trường là g, người ta đo chu kì dao động điều hòa của con lắc vào mùa hè ở nhiệt độ 400C là T1 và vào mùa đông nhiệt độ 100C là T2. Chọn nhận xét đúng
Đáp án: B Phương pháp giải: Các vật nở dài ra khi nóng lên, co lại khi lạnh đi, nên vào mùa đông, nhiệt độ thấp hơn mùa hè, dây treo con lắc sẽ co ngắn lại. Ta có công thức tính chu kì T : \(T = 2\pi \sqrt {\frac{l}{g}} \) Lời giải chi tiết: Ta có công thức tính chu kì T : \(T = 2\pi \sqrt {\frac{l}{g}} \) Vậy chu kì T tỉ lệ thuận với căn bậc 2 chiều dài con lắc Các vật nở dài ra khi nóng lên, co lại khi lạnh đi, nên vào mùa đông, nhiệt độ thấp hơn mùa hè, dây treo con lắc sẽ co ngắn lại. Nên chu kì dao động của con lắc vào mùa hè lớn hơn khi mùa đông. → T1 > T2. Chọn B Câu hỏi 38 : Tại một nơi trên mặt đất có g=9,87m/s2, một con lắc dao động điều hòa với chu kì 2s. Chiều dài của con lắc là
Đáp án: C Phương pháp giải: Công thức tính chu kì của con lắc: \(T=2\pi \sqrt{\frac{\ell }{g}}\) Lời giải chi tiết: Ta có: \(T=2\pi \sqrt{\frac{\ell }{g}}\Leftrightarrow 2=2\pi \sqrt{\frac{\ell }{9,87}}\Rightarrow \ell \approx 1\left( m \right)=100cm\) Chọn C Câu hỏi 39 : Để đo gia tốc trọng trường trung bình tại một vị trí (không yêu cầu xác định sai số), người ta dùng bộ dụng cụ gồm con lắc đơn, giá treo, thước đo chiều dài, đồng hồ bấm giây. Người ta phải thực hiện các bước: a. Treo con lắc lên giá tại nơi cần xác định gia tốc trọng trường g b. Dùng đồng hồ bấm giây để đo thời gian của một dao động toàn phần để tính được chu kì T, lặp lại phép đo 5 lần c. Kích thích cho vật nhỏ dao động d. Dùng thước đo 5 lần chiều dài của dây treo từ điểm treo tới tâm vật e. Sử dụng công thức \(\overline g = 4{\pi ^2}\dfrac{{\overline l }}{{{{\overline T }^2}}}\) để tính gia tốc trọng trường trung bình tại một vị trí đó f. Tính giá trị trung bình \(\overline l \) và \(\overline T \) Sắp xếp theo thứ tự đúng các bước trên
Đáp án: B Phương pháp giải: Sử dụng kiến thức về tiến trình thí nghiệm. Lời giải chi tiết: Thứ tự đúng các bước là: a, d, c, b, f, e. Chọn B. Câu hỏi 40 : Một con lắc đơn có chiều dài 121cm, dao động điều hòa tại nơi có gia tốc trọng trường g = 10m/s2. Lấy π2 = 10. Chu kì dao động của con lắc là
Đáp án: A Phương pháp giải: Chu kì dao động của con lắc đơn là: \(T = 2\pi \sqrt {\dfrac{l}{g}} \) Lời giải chi tiết: Chu kì dao động của con lắc là: \(T = 2\pi \sqrt {\dfrac{l}{g}} = 2\pi \sqrt {\dfrac{{1,21}}{{{\pi ^2}}}} = 2,2s\) Chọn A. Quảng cáo
|