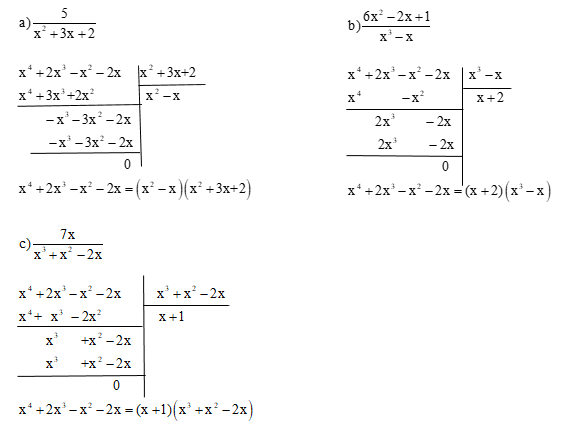10 bài tập tổng hợp Qui đồng mẫu thức nhiều phân thứcLàm bàiQuảng cáo
Câu hỏi 1 : Mẫu thức chung của 2 phân thức \(\dfrac{1}{{14{x^2}y}}\) và \(\dfrac{8}{{21x{y^5}}}\) là:
Đáp án: A Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết: MTC của \(\dfrac{1}{{14{x^2}y}}\) và \(\dfrac{8}{{21x{y^5}}}\)là: \(42{x^2}{y^5}\) Chọn A. Câu hỏi 2 : Phân thức \(\dfrac{{x - 5}}{{x - 2}}\) sau khi quy đồng mẫu thức 2 phân thức \(\dfrac{{x - 5}}{{x - 2}};\dfrac{1}{{{x^2}}}\) là:
Đáp án: C Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết: MTC: \({x^2}(x - 2)\) \(\dfrac{{x - 5}}{{x - 2}} = \dfrac{{{x^2}(x - 5)}}{{{x^2}(x - 2)}}\) Chọn C. Câu hỏi 3 : Mẫu thức chung của 3 phân thức \(\dfrac{4}{{{x^3}{y^2}}};\dfrac{7}{{4{x^5}y}}\) và \(\dfrac{5}{{12{x^5}{y^2}}}\) là:
Đáp án: D Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết: Mẫu thức chung của 3 phân thức \(\dfrac{4}{{{x^3}{y^2}}};\dfrac{7}{{4{x^5}y}}\) và \(\dfrac{5}{{12{x^5}{y^2}}}\) là: \(12{x^5}{y^2}\) Chọn D. Câu hỏi 4 : Đa thức \({x^3} - 6{x^2} + 11x - 6\) là mẫu thức chung của 2 phân thức nào sau đây:
Đáp án: A Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết: \(\dfrac{1}{{{x^2} - 4x + 3}} = \dfrac{1}{{(x - 1)(x - 3)}}\) MTC: \((x - 1)(x - 2)(x - 3) = ({x^2} - 3x + 2)(x - 3) = {x^3} - 6{x^2} + 11x - 6\) Chọn A. Câu hỏi 5 : Mẫu thức chung của các phân thức \( - 1;\dfrac{2}{{{x^2} - x + 1}};\dfrac{{3x}}{{{x^3} + 1}}\) là:
Đáp án: D Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết : Vì \({x^3} + 1 = (x + 1)({x^2} - x + 1)\) nên cả B và C đều đúng. Chọn D. Câu hỏi 6 : Quy đồng mẫu thức \(\dfrac{{x}}{{{{\left( {3x - 2} \right)}^2}}}\,\,;\dfrac{{x - 2}}{{{x}\left( {3x - 2} \right)}}\) ta sẽ “không” thu được kết quả là:
Đáp án: B Phương pháp giải: Lời giải chi tiết: Hướng dẫn giải chi tiết: \(\dfrac{{x}}{{{{\left( {3x - 2} \right)}^2}}}\, = \dfrac{{{{x}^2}}}{{x{{\left( {3x - 2} \right)}^2}}} = \,\dfrac{{{{x}^2}}}{{x{{\left( {2 - 3x} \right)}^2}}}\) (vì \({\left( {3x - 2} \right)^2}\)=\({\left( {2 - 3x} \right)^2}\)) \(\dfrac{{x - 2}}{{{x}\left( {3x - 2} \right)}} = \dfrac{{(x - 2)(3x - 2)}}{{x{{(3x - 2)}^2}}} = \dfrac{{(x - 2)(3x - 2)}}{{x{{(2 - 3x)}^2}}} = - \dfrac{{(x - 2)(2 - 3x)}}{{x{{(2 - 3x)}^2}}}\) Suy ra A, C, D đúng. B sai. Chọn B. Câu hỏi 7 : (1,5đ) Quy đồng mẫu thức các phân thức sau: a) \(\dfrac{a}{{{{(a + b)}^2}}}\) và \(\dfrac{b}{{{{(a - b)}^2}}}\) b) \(\dfrac{{x - 2}}{{x{y^2}}}\)và \(\dfrac{{1 - x}}{{12{x^3}{y^4}}}\) c) \(\dfrac{{7x - 1}}{{2{x^2} + 6x}}\) và \(\dfrac{{5 - x}}{{{x^2} - 9}}\) Phương pháp giải: Lời giải chi tiết: a) \(\dfrac{a}{{{{(a + b)}^2}}}\) và \(\dfrac{b}{{{{(a - b)}^2}}}\). MTC: \({(a + b)^2}{(a - b)^2}\). \(\begin{array}{l}\dfrac{a}{{{{(a + b)}^2}}} = \dfrac{{a{{(a - b)}^2}}}{{{{(a + b)}^2}{{(a - b)}^2}}}\\\dfrac{b}{{{{(a - b)}^2}}} = \dfrac{{b{{(a + b)}^2}}}{{{{(a + b)}^2}{{(a - b)}^2}}}\end{array}\) b) \(\dfrac{{x - 2}}{{x{y^2}}}\) và \(\dfrac{{1 - x}}{{12{x^3}{y^4}}}\) MTC: \(12{x^3}{y^4}\) \(\begin{array}{l}\dfrac{{x - 2}}{{x{y^2}}} = \dfrac{{12{x^2}{y^2}(x - 2)}}{{12{x^3}{y^4}}} = \dfrac{{12{x^3}{y^2} - 24{x^2}{y^2}}}{{12{x^3}{y^4}}}\\\dfrac{{1 - x}}{{12{x^3}{y^4}}} = \dfrac{{1 - x}}{{12{x^3}{y^4}}}\end{array}\) c) \(\dfrac{{7x - 1}}{{2{x^2} + 6x}}\) và \(\dfrac{{5 - x}}{{{x^2} - 9}}\) Ta có: \(2{x^2} + 6x = 2x(x + 3)\) \({x^2} - 9 = (x + 3)(x - 3)\) MTC: \(2x(x + 3)(x - 3)\) \(\begin{array}{l}\dfrac{{7x - 1}}{{2{x^2} + 6x}} = \dfrac{{(7x - 1)(x - 3)}}{{2x(x - 3)(x + 3)}} = \dfrac{{7{x^2} - 22x + 3}}{{2x(x - 3)(x + 3)}}\\\dfrac{{5 - x}}{{{x^2} - 9}} = \dfrac{{2x(5 - x)}}{{2x(x - 3)(x + 3)}} = \dfrac{{ - 2{x^2} + 10x}}{{2x(x - 3)(x + 3)}}\end{array}\) Câu hỏi 8 : (2đ) Quy đồng mẫu thức các thức sau: a) \(A = \dfrac{5}{{2x - 4}};B = \dfrac{4}{{3x - 9}};C = \dfrac{7}{{10 - 5x}}\) b) \(D = \dfrac{{{x^2}}}{{{x^2} - 1}};E = \dfrac{{3x - 1}}{{{x^3} + 2{x^2} + x}};F = \dfrac{{2x + 1}}{{{x^3}}}\) Phương pháp giải: Lời giải chi tiết: \(\begin{array}{l} Câu hỏi 9 : (3đ) Thực hiện phép chia: \({{\text{x}}^4} + 2{{\text{x}}^3} - {{\text{x}}^2} - 2x\) cho mẫu thức của các phân thức sau: a) \(\dfrac{5}{{{x^2} + 3x + 2}}\) b) \(\dfrac{{6{x^2} - 2x + 1}}{{{x^3} - x}}\) c) \(\dfrac{{7x}}{{{x^3} + {x^2} - 2x}}\) Phương pháp giải: Lời giải chi tiết:
Câu hỏi 10 : (0,5đ) Chứng minh \(\dfrac{{3 - 4x}}{{1 + {x^2}}} = \dfrac{{{{(2 - x)}^2}}}{{1 + {x^2}}} - 1\). Tìm \(x\) để \(A = \dfrac{{3 - 4x}}{{1 + {x^2}}}\) đạt giá trị nhỏ nhất. Phương pháp giải: Lời giải chi tiết: Ta có: \(\dfrac{{{{(2 - x)}^2}}}{{1 + {x^2}}} - 1 = \dfrac{{4 - 4x + {x^2}}}{{1 + {x^2}}} - 1 = \dfrac{{4 - 4x + {x^2}}}{{1 + {x^2}}} - \dfrac{{1 + {x^2}}}{{1 + {x^2}}} = \dfrac{{3 - 4x}}{{1 + {x^2}}}\) (đpcm) Suy ra \(A = \dfrac{{3 - 4x}}{{1 + {x^2}}} = \dfrac{{{{(2 - x)}^2}}}{{1 + {x^2}}} - 1 \geqslant - 1\) vì \(\dfrac{{{{(2 - x)}^2}}}{{1 + {x^2}}} \geqslant 0,\forall x\) Dấu “=” xảy ra \( \Leftrightarrow 2 - x = 0 \Leftrightarrow x = 2\). Vậy \(A\) đạt GTNN là \( - 1\) khi \(x = 2\). Quảng cáo
|