Đề số 4 - Đề kiểm tra học kì 2 - Toán 6

Đề bài

Phần I. Trắc nghiệm (2,0 điểm)

Hãy chọn phương án đúng và viết chữ cái đứng trước phương án đó vào bài làm.

Câu 1: Tổng tất cả các số nguyên $x$ thỏa mãn $- 2 \le x \le 2$ bằng

A. $- 2$                                 B. $- 1$

C. $0$                                     D. $2$

Câu 2: Số đối của $\dfrac{{11}}{{ - 14}}$ là

A. $- \dfrac{{11}}{{14}}$                 B. $\dfrac{{14}}{{ - 11}}$ 

C. $\dfrac{{11}}{{14}}$                                D. $\dfrac{{14}}{{11}}$

Câu 3: Phân số nghịch đảo của phân số $\dfrac{5}{{14}}$ là

A. $\dfrac{5}{{14}}$                         B. $\dfrac{{ - 5}}{{14}}$      

C. $\dfrac{{14}}{{ - 5}}$                   D. $\dfrac{{14}}{5}$ 

Câu 4: Rút gọn phân số $\dfrac{{ - 15}}{{25}}$ , ta được phân số tối giản là

A. $\dfrac{3}{5}$                              B. $\dfrac{{ - 3}}{5}$

C. $\dfrac{5}{{ - 3}}$                        D. $\dfrac{5}{3}$ 

Câu 5: Mẹ  Hằng ra chợ mua $0,4kg$ thịt lợn, biết $1kg$ thịt lợn có giá $100000$ đồng. Mẹ Hằng phải trả số tiền là

A. $60000$ đồng                    B. $40000$ đồng

C. $4000$ đồng                                  D. $6000$ đồng

Câu 6: Trên tia $Ax$ lấy hai điểm $B$ và $C$ sao cho $AC = 3cm,\,\,AB = 8cm$. Khi đó độ dài của đoạn thẳng $BC$ bằng

A. $11$                                   B. $11cm$

C. $5$                                     D. $5cm$ 

Câu 7: Góc bẹt có số đo bằng

A. $180^\circ$                      B.  $90^\circ$

C. $60^\circ$                        D. $0^\circ$

Câu 8: Trên cùng một nửa mặt phẳng bờ chứa$Ox$, vẽ hai tia $Oy$ và $Oz$ sao cho $\widehat {xOy} = 60^\circ$ và $\widehat {xOz} = 120^\circ$, khi đó

A. tia $Oy$ là  phân giác của góc $xOz$

B. tia $Oz$ là  phân giác của góc $yOx$

C. tia $Ox$ là  phân giác của góc $yOz$

D. tia $Oy$ là  phân giác của góc $yOz$

Phần II. Tự luận (8,0 điểm)

Câu 1 (2,0 điểm): Thực hiện các phép tính :

$A = \dfrac{{ - 5}}{{12}} - 3:\dfrac{9}{4}\,\,;\,\,$

$B = \left( {1\dfrac{5}{{12}} + 3.\dfrac{7}{{36}}} \right):\left( { - \dfrac{2}{{2019}}} \right)\,\,;$

$C = \dfrac{{ - 2018}}{{2019}}.\dfrac{2}{7} - \dfrac{{2018}}{{2019}}.\dfrac{5}{7} + 1\dfrac{{2018}}{{2019}}$

Câu 2 (2,0 điểm): Tìm $x$, biết

$a)\,\,x - \dfrac{2}{3} = \dfrac{7}{6}$         

$b)\,\,\left( {\dfrac{4}{3} - x} \right).\left( {\dfrac{{ - 5}}{6}} \right) = \dfrac{{ - 7}}{3}$  

Câu 3 (3,0 điểm): Vẽ tia $OA$ và $OB$ sao cho $\widehat {AOB} = 90^\circ$, lấy điểm $C$ nằm giữa hai điểm $A$ và $B$ sao cho $\widehat {AOC} = 40^\circ$.

1. Chứng minh tia $OC$ nằm giữa hai tia $OA$ và $OB$ và tính $\widehat {BOC}$.

2. Trên nửa mặt phẳng bờ chứa tia $OA$ và chứa điểm $B$, vẽ tia $OD$ sao cho $\widehat {AOD} = 140^\circ$.

a) Tính $\widehat {BOD}$.

b) Chứng minh $OB$ là tia phân giác của $\widehat {COD}$.

Câu 4 (1,0 điểm): 

1) Tính nhanh : $S = 1 + \dfrac{1}{{1 + 2}} + \dfrac{1}{{1 + 2 + 3}} + \dfrac{1}{{1 + 2 + 3 + 4}} +$ $... + \dfrac{1}{{1 + 2 + 3 + 4 + ... + 8}}$

2) Tìm số dư khi chia $A = 1 + 5 + {5^2} + {5^3} + {5^4}$$+ {5^5} + {5^6} + {5^7} + {5^8} + {5^9}$ cho $31$.

Đ/a TN

Câu 1

Phương pháp:

Liệt kê các số nguyên $- 2 \le x \le 2$ rồi tính tổng của tất cả các số đó.

Cách giải:

Các số nguyên  $x$ thỏa mãn $- 2 \le x \le 2$ là $x \in \left\{ { - 2; - 1;0;1;2} \right\}$.

Tổng tất cả các số nguyên $x$ thỏa mãn $- 2 \le x \le 2$ là :

$\left( { - 2} \right) + \left( { - 1} \right) + 0 + 1 + 2$ $= \left[ {\left( { - 2} \right) + 2} \right] + \left[ {\left( { - 1} \right) + 1} \right] + 0$$= 0 + 0 + 0 = 0$

Chọn C.

Câu 2

Phương pháp:

Số đối của phân số $\dfrac{a}{b}$ là $- \dfrac{a}{b}$ (hoặc $\dfrac{{ - a}}{b}$ hoặc $\dfrac{a}{{ - b}}$).

Cách giải:

Số đối của $\dfrac{{11}}{{ - 14}}$ là  $\dfrac{{11}}{{14}}$.

Chọn C.

Câu 3

Phương pháp:

Phân số nghịch đảo của phân số $\dfrac{a}{b}$ là $\dfrac{b}{a}$ ($a,\,\,b$ khác $0$).

Cách giải:

Phân số nghịch đảo của phân số $\dfrac{5}{{14}}$ là $\dfrac{{14}}{5}$.

Chọn D.

Câu 4

Phương pháp:

Muốn rút gọn một phân số, ta chia cả tử và mẫu của phân số cho một ước chung (khác $1$ và $- 1$) của chúng.

Cách giải:

Ta có : $\dfrac{{ - 15}}{{25}} = \dfrac{{ - 15:5}}{{25:5}} = \dfrac{{ - 3}}{5}$.

Vậy rút gọn phân số $\dfrac{{ - 15}}{{25}}$ , ta được phân số tối giản là $\dfrac{{ - 3}}{5}$.

Chọn B.

Câu 5

Phương pháp:

Để tìm số tiền mẹ Hằng phải trả ta lấy $100000$ nhân với $0,4$ sau đó ghi thêm đơn vị vào kết quả.

Cách giải:

Mẹ Hằng phải trả số tiền là : $100000 \times 0,4 = 40000$ (đồng).

Chọn B.

Câu 6

Phương pháp:

- Áp dụng nhận xét: Trên tia$Ox,{\rm{ }}OM = a,{\rm{ }}ON = b$ , nếu $0 < a < b$ thì điểm $M$ nằm giữa hai điểm $O$ và $N$.

- Áp dụng tính chất: Nếu điểm  $M$ nằm giữa hai điểm $A$ và $B$ thì$AM + MB = AB$.

Cách giải:

Trên tia $Ax$ ta có $AC < AB\,\,\left( {do\,\,3cm < 8cm} \right)$ nên điểm $C$ là điểm nằm giữa hai điểm $A$ và $B$

$\begin{array}{l} \Rightarrow AC + CB = AB\\ \Rightarrow CB = AB - AC = 8 - 3 = 5\,\,\left( {cm} \right)\end{array}$

Vậy độ dài đoạn thẳng $BC$ là $5cm$.

Chọn D.

Câu 7

Phương pháp:

Xem lại định nghĩa về góc bẹt.

Cách giải:

Góc bẹt có số đo bằng $180^\circ$.

Chọn A.

Câu 8

Phương pháp:

Áp dụng các nhận xét:

- Trên cùng một nửa mặt phẳng bờ chứa tia $Ox$, nếu $\widehat {xOy} < \widehat {xOz}$ thì tia $Oy$ nằm giữa hai tia $Ox$ và $Oz$.

- Nếu tia $Oy$ nằm giữa hai tia $Ox$ và $Oz$ thì $\widehat {xOy} + \widehat {yOz} = \widehat {xOz}$. Ngược lại, nếu $\widehat {xOy} + \widehat {yOz} = \widehat {xOz}$ thì tia $Oy$ nằm giữa hai tia $Ox$ và $Oz$.

Cách giải: 

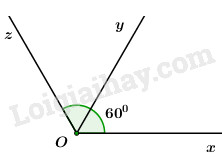
Trên cùng một nửa mặt phẳng bờ chứa tia $Ox$, ta có  $\widehat {xOy} < \,\widehat {xOz}\,\,\,\left( {{{60}^0}\, < {{120}^0}} \right)$ nên tia $Oy$ là tia nằm giữa hai tia $Ox$ và $Oz$

$\Rightarrow \widehat {xOy} + \widehat {yOz} = \widehat {xOz}$$\Rightarrow \widehat {yOz} = \widehat {xOz} - \widehat {xOby}$$= {120^0} - {60^0} = {60^0}$ 

Ta có tia $Oy$ là tia nằm giữa hai tia $Ox$ và $Oz$.

Lại có $\widehat {xOy} = \,\widehat {yOz} = {60^0}$

Suy ra $Oy$ là tia phân giác của $\widehat {xOz}$.

Chọn A

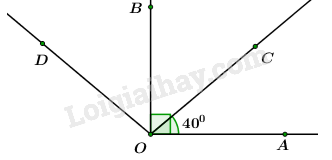
LG câu 1

Phương pháp giải:

Áp dụng các quy tắc :

+) Thứ tự thực hiện các phép tính đối với biểu thức không có dấu ngoặc:

Lũy thừa $\to$ Nhân và chia $\to$ Cộng và trừ

+) Thứ tự thực hiện các phép tính đối với biểu thức có dấu ngoặc: $(\,\,)\,\, \to {\rm{[}}\,\,{\rm{]}}\,\, \to {\rm{\{ }}\,\,{\rm{\} }}$

Lời giải chi tiết:

$\begin{array}{l}A = \dfrac{{ - 5}}{{12}} - 3:\dfrac{9}{4}\\\,\,\,\,\, = \dfrac{{ - 5}}{{12}} - 3.\dfrac{4}{9}\\\,\,\,\,\, = \dfrac{{ - 5}}{{12}} - \dfrac{4}{3}\\\,\,\,\, = \dfrac{{ - 5}}{{12}} - \dfrac{{16}}{{12}}\\\,\,\,\, = \dfrac{{ - 21}}{{12}} = \dfrac{{ - 7}}{4}\end{array}$

$\begin{array}{l}B = \left( {1\dfrac{5}{{12}} + 3.\dfrac{7}{{36}}} \right):\left( { - \dfrac{2}{{2019}}} \right)\\\,\,\,\,\, = \left( {\dfrac{{17}}{{12}} + \dfrac{{3.7}}{{36}}} \right):\left( {\dfrac{{ - 2}}{{2019}}} \right)\\\,\,\,\,\, = \left( {\dfrac{{17}}{{12}} + \dfrac{7}{{12}}} \right).\dfrac{{2019}}{{ - 2}}\\\,\,\,\, = \dfrac{{24}}{{12}}.\dfrac{{2019}}{{ - 2}}\\\,\,\,\, = 2.\dfrac{{2019}}{{ - 2}}\\\,\,\,\, =  - 2019\end{array}$

$C = \dfrac{{ - 2018}}{{2019}}.\dfrac{2}{7} - \dfrac{{2018}}{{2019}}.\dfrac{5}{7} + 1\dfrac{{2018}}{{2019}}$

$= \dfrac{{ - 2018}}{{2019}}.\dfrac{2}{7} + \dfrac{{ - 2018}}{{2019}}.\dfrac{5}{7}$$+ \left( {1 + \dfrac{{2018}}{{2019}}} \right)$

$\begin{array}{l} = \dfrac{{ - 2018}}{{2019}}.\left( {\dfrac{2}{7} + \dfrac{5}{7}} \right) + 1 + \dfrac{{2018}}{{2019}}\\ = \dfrac{{ - 2018}}{{2019}}.\dfrac{7}{7} + 1 + \dfrac{{2018}}{{2019}}\\ = \dfrac{{ - 2018}}{{2019}} + 1 + \dfrac{{2018}}{{2019}}\\ = \dfrac{{ - 2018}}{{2019}} + \dfrac{{2018}}{{2019}} + 1\\ = 0 + 1 = 1\end{array}$

LG câu 2

Phương pháp giải:

Áp dụng quy tắc chuyển vế: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” thành dấu “+”.

Lời giải chi tiết:

$\begin{array}{l}a)\,\,x - \dfrac{2}{3} = \dfrac{7}{6}\\\,\,\,\,\,\,\,x = \dfrac{7}{6} + \dfrac{2}{3}\\\,\,\,\,\,\,\,x = \dfrac{{11}}{6}\end{array}$

Vậy $x = \dfrac{{11}}{6}.$ 

$\begin{array}{l}b)\,\,\left( {\dfrac{4}{3} - x} \right).\left( {\dfrac{{ - 5}}{6}} \right) = \dfrac{{ - 7}}{3}\\\,\,\,\,\,\,\,\dfrac{4}{3} - x = \dfrac{{ - 7}}{3}:\dfrac{{ - 5}}{6}\\\,\,\,\,\,\,\,\dfrac{4}{3} - x = \dfrac{{14}}{5}\\\,\,\,\,\,\,\,x = \dfrac{4}{3} - \dfrac{{14}}{5}\\\,\,\,\,\,\,\,x = \dfrac{{ - 22}}{{15}}\end{array}$

Vậy $x =  - \dfrac{{22}}{{15}}.$

LG câu 3

Phương pháp giải:

Áp dụng các nhận xét:

- Trên cùng một nửa mặt phẳng bờ chứa tia $Ox$, nếu $\widehat {xOy} < \widehat {xOz}$ thì tia $Oy$ nằm giữa hai tia $Ox$ và $Oz$.

- Nếu tia $Oy$ nằm giữa hai tia $Ox$ và $Oz$ thì $\widehat {xOy} + \widehat {yOz} = \widehat {xOz}$. Ngược lại, nếu $\widehat {xOy} + \widehat {yOz} = \widehat {xOz}$ thì tia $Oy$ nằm giữa hai tia $Ox$ và $Oz$.

Lời giải chi tiết:

1) Chứng minh tia $OC$ nằm giữa hai tia $OA$ và $OB$ và tính $\widehat {BOC}$.

Trên cùng một nửa mặt phẳng bờ chứa tia $OA$, ta có $\widehat {AOC} < \,\widehat {AOB}\,\,\left( {{{40}^0}\, < {{90}^0}} \right)$ nên tia $OC$ là tia nằm giữa hai tia $OA$ và $OB$

$\Rightarrow \widehat {AOC} + \widehat {COB} = \widehat {AOB}$

$\Rightarrow \widehat {COB} = \widehat {AOB} - \widehat {AOC}$$= {90^0} - {40^0} = {50^0}$

Vậy $\widehat {BOC} = 50^\circ$.

2) Trên nửa mặt phẳng bờ chứa tia $OA$ và chứa điểm $B$, vẽ tia $OD$ sao cho $\widehat {AOD} = 140^\circ$.

a) Tính $\widehat {BOD}$.

Trên cùng một nửa mặt phẳng bờ chứa tia $OA$, ta có  $\widehat {AOB} < \,\widehat {AOD}\,\,\left( {{{90}^0}\, < {{140}^0}} \right)$nên tia $OB$ là tia nằm giữa hai tia $OA$ và $OD$

$\Rightarrow \widehat {AOB} + \widehat {BOD} = \widehat {AOD}$

$\Rightarrow \widehat {BOD} = \widehat {AOD} - \widehat {AOB}$$= {140^0} - {90^0} = {50^0}$

Vậy $\widehat {BOD} = 50^\circ$.

b) Chứng minh $OB$ là tia phân giác của $\widehat {COD}$.

Trên cùng một nửa mặt phẳng bờ chứa tia $OA$, ta có  $\widehat {AOC} < \,\widehat {AOD}\,\,\left( {{{40}^0}\, < {{140}^0}} \right)$ nên tia $OC$ là tia nằm giữa hai tia $OA$ và $OD$

$\Rightarrow \widehat {AOC} + \widehat {COD} = \widehat {AOD}$

$\Rightarrow \widehat {COD} = \widehat {AOD} - \widehat {AOC}$$= {140^0} - {40^0} = {100^0}$

Ta có : $\widehat {BOC} = \widehat {BOD}$$= \dfrac{1}{2}\widehat {COD}\,\,\left( { = 50^\circ } \right)$

Suy ra $OB$ là tia phân giác của $\widehat {COD}$.

LG câu 4

Phương pháp giải:

1) Đưa tổng đã cho về dạng: $S = 1 + \dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{36}}.$ 

+) Tính $\dfrac{1}{2}S$ sau đó suy ra giá trị của biểu thức $S.$

2) Nhóm $A$  thành các nhóm tương ứng rồi tìm số dư của tổng $A$ cho $31.$

Lời giải chi tiết:

1) Tính nhanh : $S = 1 + \dfrac{1}{{1 + 2}} + \dfrac{1}{{1 + 2 + 3}} + \dfrac{1}{{1 + 2 + 3 + 4}}$ $+ ... + \dfrac{1}{{1 + 2 + 3 + 4 + ... + 8}}$

$S = 1 + \dfrac{1}{{1 + 2}} + \dfrac{1}{{1 + 2 + 3}} + \dfrac{1}{{1 + 2 + 3 + 4}}$$+ ... + \dfrac{1}{{1 + 2 + 3 + 4 + ... + 8}}$

$= 1 + \dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{36}}$

$\Rightarrow \dfrac{1}{2}.S = \dfrac{1}{2}\left( {1 + \dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{36}}} \right)$

$= \dfrac{1}{2} + \dfrac{1}{6} + \dfrac{1}{{12}} + \dfrac{1}{{20}} + ... + \dfrac{1}{{72}}$

$= \dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \dfrac{1}{{4.5}}$$+ ... + \dfrac{1}{{8.9}}$

$1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4}$$+ \dfrac{1}{4} - \dfrac{1}{5} + ... + \dfrac{1}{8} - \dfrac{1}{9}$

$\begin{array}{l}\, = 1 - \dfrac{1}{9} = \dfrac{8}{9}\\ \Rightarrow \dfrac{1}{2}S = \dfrac{8}{9}\\ \Rightarrow S = \dfrac{8}{9}:\dfrac{1}{2} = \dfrac{{16}}{9}.\end{array}$

2) Tìm số dư khi chia $A = 1 + 5 + {5^2} + {5^3} + {5^4}$$+ {5^5} + {5^6} + {5^7} + {5^8} + {5^9}$  cho $31$.

$A = 1 + 5 + {5^2} + {5^3} +$${5^4} + {5^5} + {5^6} + {5^7} + {5^8} + {5^9}$

$= 1 + \left( {5 + {5^2} + {5^3}} \right)$$+ \left( {{5^4} + {5^5} + {5^6}} \right)$$+ \left( {{5^7} + {5^8} + {5^9}} \right)$

$= 1 + 5.\left( {1 + 5 + {5^2}} \right)$$+ {5^4}.\left( {1 + 5 + {5^2}} \right)$$+ {5^7}.\left( {1 + 5 + {5^2}} \right)$

$= 1 + 5.31 + {5^4}.31 + {5^7}.31$

$= 1 + 31.\left( {5 + {5^4} + {5^7}} \right)$ 

Lại có $31.\left( {5 + {5^4} + {5^7}} \right)$ chia hết cho $31$.

Do đó $A = 1 + 31.\left( {5 + {5^4} + {5^7}} \right)$ chia cho $31$ dư $1$.

Vậy số dư khi chia $A = 1 + 5 + {5^2} + {5^3} + {5^4}$$+ {5^5} + {5^6} + {5^7} + {5^8} + {5^9}$ cho $31$ là $1$.

Nguồn sưu tầm

Loigiaihay.com