Đề số 5 - Đề kiểm tra học kì 2 - Toán 6

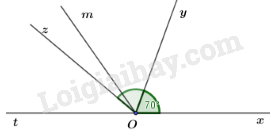
Đề bài

Bài 1 (3 điểm) Thực hiện phép tính (tính nhanh nếu có thể):

\(a)\,\dfrac{1}{5} + \dfrac{{ - 5}}{{19}} + \dfrac{4}{5} + \dfrac{{ - 4}}{{19}}\)

\(b)\,\dfrac{1}{5}.\dfrac{{11}}{{16}} + \dfrac{1}{5}.\dfrac{5}{{16}} + \dfrac{4}{5}\)

\(c)\,50\%  - 1\dfrac{1}{2} + 0,5.\dfrac{3}{8}\)

\(d)\,{\left( {\dfrac{{ - 1}}{6}} \right)^2}:\dfrac{5}{{ - 24}} + \left( {\dfrac{7}{{25}} - 36\% } \right).\left| { - 8\dfrac{1}{3}} \right|\)

Bài 2 (2,5 điểm) Tìm \(x\)

\(a)\,x - \dfrac{1}{2} = \dfrac{3}{4}\)

\(b)\,\dfrac{2}{3} + \dfrac{3}{4}x =  - \dfrac{5}{6}\)

\(c)\,\left| {\dfrac{2}{3} + x} \right| - \dfrac{1}{3} = \dfrac{2}{3}\)

Bài 3 (1,5 điểm) Trong đợt phát động vì Trường Sa thân yêu. Học sinh ba lớp 6A; 6B; 6C đóng góp được 140 quyển sách trong đó số sách lớp 6A góp được chiếm \(\dfrac{1}{5}\) số quyển sách của ba lớp. Số sách lớp 6B góp được chiếm 25% số quyển sách của ba lớp. Hỏi mỗi lớp góp được bao nhiêu quyển sách?

Bài 4 (2 điểm) Trên cùng một nửa mặt phẳng bờ chứa tia Ox vẽ hai tia Oy, Oz sao cho \(\angle xOy = {70^0}\) và \(\angle xOz = {140^0}\).

a) Tính \(\angle yOz\).

b) Hỏi tia Oy có phải là tia phân giác của góc \(xOz\) không? Vì sao?

c) Vẽ tia Ot là tia đối của tia Ox và vẽ tia Om là tia phân giác của góc \(yOt.\) Tính góc \(xOm.\)

Bài 5 (1 điểm) Nhân dịp quốc tế thiếu nhi 1 tháng 6 một cửa hàng có giảm giá 30% trên tất cả các loại hàng như sau :

Em hãy giúp người bán hàng tính giá mới.

LG câu 1

Phương pháp giải:

a) Nhóm các phân số có cùng mẫu số, rồi thực hiện phép tính cộng hai phân số có cùng mẫu số. Muốn cộng hai phân số có cùng mẫu số ta cộng tử với tử và giữ nguyên mẫu.

b) Thực hiện nhóm như sau: \(\dfrac{1}{5}.\dfrac{{11}}{{16}} + \dfrac{1}{5}.\dfrac{5}{{16}} + \dfrac{4}{5}\)\( = \dfrac{1}{5}.\left( {\dfrac{{11}}{{16}} + \dfrac{5}{{16}}} \right) + \dfrac{4}{5}\) rồi sau đó thực hiện phép tính theo thứ tự ưu tiên. Thực hiện phép tính trong ngoặc trước, ngoài ngoặc sau. Nhân chia trước cộng trừ sau.

c) Viết số phần trăm, hỗ số, số thập phân dưới dạng phân số, rồi thực hiện phép tính theo thứ tự nhân chia trước, cộng trừ sau.

d) Thực hiện phép tính lũy thừa, chuyển số phần trăm , hỗ số về phân số. Thực hiện phép tính theo thứ tự ưu tiên: nhân chia trước, cộng trừ sau. Trong ngoặc trước, ngoài ngoặc sau.

Lời giải chi tiết:

\(\begin{array}{l}a)\,\dfrac{1}{5} + \dfrac{{ - 5}}{{19}} + \dfrac{4}{5} + \dfrac{{ - 4}}{{19}}\\ = \left( {\dfrac{1}{5} + \dfrac{4}{5}} \right) + \left( {\dfrac{{ - 5}}{{19}} + \dfrac{{ - 4}}{{19}}} \right)\\ = 1 + \dfrac{{ - 9}}{{19}} = \dfrac{{10}}{{19}}\end{array}\)

\(\begin{array}{l}b)\,\dfrac{1}{5}.\dfrac{{11}}{{16}} + \dfrac{1}{5}.\dfrac{5}{{16}} + \dfrac{4}{5}\\ = \dfrac{1}{5}.\left( {\dfrac{{11}}{{16}} + \dfrac{5}{{16}}} \right) + \dfrac{4}{5}\\ = \dfrac{1}{5}.1 + \dfrac{4}{5} = 1\end{array}\)

\(\begin{array}{l}c)\,50\%  - 1\dfrac{1}{2} + 0,5.\dfrac{3}{8}\\ = \dfrac{{50}}{{100}} - \dfrac{3}{2} + \dfrac{1}{2}.\dfrac{3}{8}\\ = \dfrac{1}{2} - \dfrac{3}{2} + \dfrac{3}{16}\\ =  - 1 + \dfrac{3}{16}\\ = \dfrac{{ - 13}}{16}\end{array}\)

\(\begin{array}{l}d)\,{\left( {\dfrac{{ - 1}}{6}} \right)^2}:\dfrac{5}{{ - 24}} + \left( {\dfrac{7}{{25}} - 36\% } \right).\left| { - 8\dfrac{1}{3}} \right|\\ = \dfrac{1}{{36}}:\dfrac{5}{{ - 24}} + \left( {\dfrac{7}{{25}} - \dfrac{{36}}{{100}}} \right).\dfrac{{25}}{3}\\ = \dfrac{1}{{36}}.\dfrac{{ - 24}}{5} + \left( {\dfrac{{28}}{{100}} - \dfrac{{36}}{{100}}} \right).\dfrac{{25}}{3}\\ = \dfrac{{ - 2}}{{15}} + \dfrac{{ - 8}}{{100}}.\dfrac{{25}}{3}\\ = \dfrac{{ - 2}}{{15}} + \dfrac{{ - 2}}{3}\\ = \dfrac{{ - 2}}{{15}} + \dfrac{{ - 10}}{{15}}\\ = \dfrac{{ - 12}}{{15}} = \dfrac{{ - 4}}{5}\end{array}\)

LG câu 2

Phương pháp giải:

a) Chuyển \(\dfrac{{ - 1}}{2}\) từ vế trái sang vế phải đổi dấu thành \( + \dfrac{1}{2}\). Rồi thực hiện phép cộng ở vế phải, ta tìm được giá trị của x.

b) Tìm \(\dfrac{3}{4}x\) ta chuyển \(\dfrac{2}{3}\) từ vế trái qua vế phải đổi dấu thành \(\dfrac{{ - 2}}{3}\). Thực hiện phép tính bên vế phải, được kết quả bao nhiêu ta đem chia cho \(\dfrac{3}{4}\) thì tìm ra x.

c) Tìm x trong dấu giá trị tuyệt đối. Ta tìm \(\left| {\dfrac{2}{3} + x} \right|\) bằng cách chuyển \(\dfrac{{ - 1}}{3}\) từ vế trái qua vế phải, rồi ta thực hiện phép tính bên vế phải. Sau đó chia hai 2 trường hợp để tìm x.

Lời giải chi tiết:

\(\begin{array}{l}a)\,x - \dfrac{1}{2} = \dfrac{3}{4}\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \dfrac{3}{4} + \dfrac{1}{2}\\\,\,\,\,\,x\,\,\,\,\,\,\,\,\,\, = \dfrac{5}{4}\end{array}\)

Vậy \(x=\drac{5}{4}\)

\(\begin{array}{l}b)\,\dfrac{2}{3} + \dfrac{3}{4}x =  - \dfrac{5}{6}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{3}{4}x =  - \dfrac{5}{6} - \dfrac{2}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{3}{4}x = \dfrac{{ - 3}}{2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{{ - 3}}{2}:\dfrac{3}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \dfrac{{ - 3}}{2}.\dfrac{4}{3}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x =  - 2\end{array}\)

Vậy \(x=-2\)

\(\begin{array}{l}c)\,\left| {\dfrac{2}{3} + x} \right| - \dfrac{1}{3} = \dfrac{2}{3}\\\,\,\,\,\,\left| {\dfrac{2}{3} + x} \right|\,\,\,\,\,\,\,\,\,\, = \dfrac{2}{3} + \dfrac{1}{3}\\\,\,\,\,\,\left| {\dfrac{2}{3} + x} \right|\,\,\,\,\,\,\,\,\,\, = 1\end{array}\)

TH1:

\(\begin{array}{l}\dfrac{2}{3} + x = 1\\x = 1 - \dfrac{2}{3}\\x = \dfrac{1}{3}\,\,\,\,\end{array}\)

TH2: 

\(\begin{array}{l}\dfrac{2}{3} + x =  - 1\\x =  - 1 - \dfrac{2}{3}\\x =  - \dfrac{5}{3}\,\,\,\end{array}\)

Vậy \(x = \dfrac{1}{3}\) hoặc \(x =  - \dfrac{5}{3}\)

LG câu 3

Phương pháp giải:

Muốn tìm số sách lớp 6A khuyên góp được ta tính \(\dfrac{1}{5}\) của 140.

Muốn tìm số sách lớp 6B góp được ta tính \(25\% \) của 140.

Để tìm số sách lớp 6C ta lấy tổng số sách của cả 3 lớp trừ đi số sách của hai lớp 6A và 6B. 

Lời giải chi tiết:

Số sách lớp 6A góp được là: \(140.\dfrac{1}{5} = 28\) (quyển)

Số sách lớp 6B góp được là: \(25\% .140 = 35\) (quyển)

Số sách lớp 6C góp được là: \(140 - 28 - 35 = 77\) (quyển)

Đáp số: 6A: 28 quyển; 6B: 35 quyển; 6C: 77 quyển.

LG câu 4

Phương pháp giải:

a) Muốn tìm được \(\angle yOz\) ta chứng minh Oy là tia nằm giữa hai tia Ox và Oz. Từ đó: \(\angle xOy + \angle yOz = \angle xOz\)

Thay số đo các góc đã biết vào ta tìm được \(\angle yOz\)

b) Khẳng định tia Oy là tia phân  giác của góc xOz. Ta chứng minh: chỉ ra Oy là tia nằm giữa hai tia Ox và Oz, và \(\angle xOy = \angle yOz = \dfrac{{\angle xOz}}{2}\)

c) Vẽ tia Ot là tia đối của tia Ox và vẽ tia Om là tia phân giác của góc \(yOt.\) \(Tia\,\,Oy\) nằm giữa hai tia Ox và Om. Từ đó suy ra: \(\angle xOy + \angle yOm = \angle xOm\). Thay số đo các góc đã biết vào ta tìm được góc \(\angle xOm.\)

Lời giải chi tiết:

a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\angle xOy < \angle xOz\,\,\left( {{{70}^0} < {{140}^0}} \right)\)

\( \Rightarrow Tia\,\,Oy\) nằm giữa hai tia \(Ox;\,Oz\)

\(\begin{array}{l} \Rightarrow \angle xOy + \angle yOz = \angle xOz\\\,\,\,\,\,\,\,\,{70^0}\,\,\,\,\, + \angle yOz = {140^0}\\ \Rightarrow \angle yOz = {140^0} - {70^0} = {70^0}\end{array}\)

b) Ta có: Tia Oy nằm giữa tia Ox và tia Oz

và \(\angle xOy = \angle yOz = {70^0}\)

\( \Rightarrow Tia\,\,Oy\) là tia phân giác của góc \(\angle xOz\)

c) Vẽ tia Ot là tia đối của tia Ox và vẽ tia Om là tia phân giác của góc \(yOt.\) Tính góc \(xOm.\)

Vì Ot là tia đối của tia Ox nên \(\angle xOt = {180^0}\).

Trên nửa mặt phẳng bờ chứa tia Ox, ta có: \(\angle xOy < \angle xOt\,\,\left( {{{70}^0} < {{180}^0}} \right)\)

\( \Rightarrow Tia\,\,Oy\) nằm giữa hai tia Ox và Ot

\(\begin{array}{l} \Rightarrow \angle xOy + \angle yOt = \angle xOt\\\,\,\,\,\,\,\,\,\,\,{70^0}\,\,\, + \angle yOt = {180^0}\\ \Rightarrow \angle yOt = {180^0} - {70^0} = {110^0}\end{array}\)

Om là tia phân giác của góc \(\angle yOt\) nên:

+ Tia Om nằm giữa hai tia Ot và Oy

+ \(\angle yOm = \angle mOt = \dfrac{{\angle yOt}}{2} \)\(= \dfrac{{{{110}^0}}}{2} = {55^0}\)

Vì tia Oy nằm giữa hai tia Ox và Ot,

Tia Om nằm giữa hai tia Ot và Oy (do Om là tia phân giác góc yOt)

\( \Rightarrow Tia\,\,Oy\) nằm giữa hai tia Ox và Om.

Do đó:

\(\begin{array}{l}\angle xOy + \angle yOm = \angle xOm\\{70^0} + {55^0} = \angle xOm\\ \Rightarrow \angle xOm = {125^0}\end{array}\)

Vậy \(\angle xOm = {125^0}\).

LG câu 5

Phương pháp giải:

Vì cửa hàng giảm 30% trên tất cả các mặt hàng. Nên nếu tính giá mới ta cần tính:

Giá mới = (100% - 30%) .Giá cũ  

Hay:  Giá mới = 70%. Giá cũ.

Lời giải chi tiết:

Ta có bảng giá đầy đủ như sau:

Nguồn sưu tầm

Loigiaihay.com