Đề số 1 - Đề kiểm tra học kì 2 - Toán 6

Đề bài

I. TRẮC NGHIỆM (2 ĐIỂM)

Chọn đáp án đúng

Câu 1: Phân số tối giản của phân số \(\dfrac{{20}}{{ - 140}}\) là:

A.\(\dfrac{{10}}{{ - 70}}\)                      B.\(\dfrac{{ - 4}}{{28}}\)           

C.\(\dfrac{2}{{ - 14}}\)              D.\(\dfrac{{ - 1}}{7}\)

Câu 2: Kết quả của phép chia \(\dfrac{5}{9}:\dfrac{{ - 7}}{3}\) là:

A.\( - \dfrac{5}{{21}}\)             B.\( - \dfrac{{35}}{{27}}\)

C.\(\dfrac{5}{{21}}\)                             D. Một kết quả khác

Câu 3: \(\dfrac{3}{4}\) của 60 là :

A.\(30\)                                   B. \(40\)

C.\(45\)                                   D.\(50\)

Câu 4: Giá trị của a bằng bao nhiêu nếu \(\dfrac{2}{5}\) của a bằng 4 ?

A.\(10\)                                   B.\(12\)

C.\(14\)                                   D.\(16\)

Câu 5: Biết \(\angle xOy = {70^0},\angle aOb = {110^0}\) . Hai góc trên là hai góc

A. Phụ nhau                            B. Kề nhau

C. Bù nhau                              D. Kề bù

Câu 6: \(Ot\) là tia phân giác của góc \(xOy\) nếu :

A. Tia Ot nằm giữa hai tia \(Ox\) và \(Oy\)

B. \(\angle xOt = \angle yOt = \dfrac{1}{2}\angle xOy\)

C.\(\angle xOt = \angle yOt\)

D. Cả ba phương án trên đều sai

II. TỰ LUẬN (8 ĐIỂM)

Bài 1 (1,5 điểm) Thực hiện phép tính sau:

\(a)\,\dfrac{{31}}{{17}} + \dfrac{{ - 5}}{{13}} + \dfrac{{ - 8}}{{13}} - \dfrac{{14}}{{17}}\)   

\(b)\,7\dfrac{5}{{11}} - \left( {2\dfrac{3}{7} + 3\dfrac{5}{{11}}} \right)\)

Bài 2 (1,5 điểm) Tìm x, biết:

\(a)\,x + \dfrac{1}{2} = \dfrac{{ - 3}}{4}\)           

\(b)\,{\left( {x + 3} \right)^3} = 8\)        

\(c)\,3.\left| x \right| - \dfrac{1}{3} = \dfrac{8}{3}\)

Bài 3 (2 điểm) Có một tập bài kiểm tra gồm 45 bài được xếp thành ba loại: Giỏi, khá và trung bình. Trong đó số bài đạt điểm giỏi bằng \(\dfrac{1}{3}\) tổng số bài kiểm tra. Số bài đạt điểm khá bằng \(90\% \) số bài còn lại.

a) Tính số bài trung bình.

b) Tính tỷ số phần trăm số bài đạt điểm trung bình so với tổng số bài kiểm tra.

Bài 4 (2,5 điểm) Trên cùng một nửa mặt phẳng bờ chứa tia \(Oa\) , vẽ tia \(Ob\) sao cho \(\angle aOb = {50^0}\) , vẽ tia \(Oc\) sao cho \(\angle aOc = {100^o}\)

a) Tính số đo góc \(\angle bOc.\)

b) Tính \(Ob\) có phải là tia phân giác của góc \(aOc\) không? Vì sao?

c) Vẽ tia \(Oa'\) là tia đối của tia \(Oa\) . Tính số đo góc \(bOa'\)

d) Vẽ đường tròn \(\left( {O;2cm} \right)\) cắt đường thẳng \(aa'\) tại hai điểm \(M,N.\) Trên tia \(Oa\) lấy điểm \(P\) sao cho \(OP = 5cm.\) Tính độ dài đoạn thẳng \(MP.\)

Bài 5 (0,5 điểm) Cho \(S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + ... + \dfrac{5}{{{{100}^2}}}.\) Chứng tỏ rằng \(2 < S < 5\)

Đ/a TN

Câu 1: 

Phương pháp:

Rút gọn phân số \(\dfrac{{20}}{{ - 140}}\) bằng cách chia cả tử và mẫu của phân số cho 20. Ta tìm được phân số tối giản của nó.

Cách giải:

Ta có: \(\dfrac{{20}}{{ - 140}} = \dfrac{{20:20}}{{ - 140:20}}\)\( = \dfrac{1}{{ - 7}} = \dfrac{{ - 1}}{7}\)

Chọn D

Câu 2:

Phương pháp:

Muốn chia một phân số hay một số nguyên cho một phân số, ta nhân số bị chia với số nghịch đảo của số chia.

\(\dfrac{a}{b}:\dfrac{c}{d} = \dfrac{a}{b}.\dfrac{d}{c} = \dfrac{{a.d}}{{b.c}};\,\,\,\) \(a:\dfrac{c}{d} = a.\dfrac{d}{c} = \dfrac{{a.d}}{c}\,\,\,\left( {c \ne 0} \right)\)

Cách giải:

\(\dfrac{5}{9}:\dfrac{{ - 7}}{3} = \dfrac{5}{9}.\dfrac{3}{{ - 7}}\)\( = \dfrac{{5.3}}{{9.\left( { - 7} \right)}}\)\( = \dfrac{5}{{ - 21}} = \dfrac{{ - 5}}{{21}}\)

Chọn A.

Câu 3:

Phương pháp:

Muốn tìm \(\dfrac{3}{4}\) của một số \(60\) cho trước, ta tính \(60.\dfrac{3}{4}\,\)

Cách giải:

Ta có:

\(\dfrac{3}{4}\) của 60 là : \(\dfrac{3}{4}.60 = 45\)

Chọn C.

Câu 4:

Phương pháp:

Muốn tìm một số biết \(\dfrac{m}{n}\) của nó bằng \(a\) , ta tính \(a:\dfrac{m}{n}\left( {m,n \in {N^*}} \right)\)

Cách giải:

Giá trị của \(a\) là: \(4:\dfrac{2}{5} = 4.\dfrac{5}{2}\) \( = \dfrac{{4.5}}{2} = 10\)

Chọn A

Câu 5:

Phương pháp: Tính tổng của hai góc, ta nhận thấy tổng của nó bằng \({180^0}\).

Mà tổng hai góc bằng  \({180^0}\)thì hai góc đó gọi là hai góc bù nhau.

Cách giải:

Ta có:

\(\angle xOy = {70^0},\angle aOb = {110^0}\)

\( \Rightarrow \angle xOy + \angle aOb\)\( = {70^0} + {110^0} = {180^0}\)

\( \Rightarrow \angle xOy;\angle aOb\) là hai góc bù nhau.

Chọn C

Câu 6:

Phương pháp: Định nghĩa tia phân giác của một góc: Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.

Cách giải:

\(Ot\) là tia phân giác của góc \(xOy\) nếu : \(\angle xOt = \angle yOt = \dfrac{1}{2}\angle xOy\)

Chọn B.

LG bài 1

Phương pháp giải:

a) Nhóm các số hạng có cùng mẫu số, rồi thực hiện cộng trừ các phân số có cùng mẫu số.

b) Tách hỗn số thành hai phần: phần nguyên và phần phân số, rồi cộng phần nguyên với nhau, cộng phần phân số với nhau. 

Chú ý: Muốn cộng (trừ) hai phân số có cùng mẫu số, ta cộng (trừ) tử số với nhau và giữ nguyên mẫu số.

Lời giải chi tiết:

\(\begin{array}{l}a)\,\dfrac{{31}}{{17}} + \dfrac{{ - 5}}{{13}} + \dfrac{{ - 8}}{{13}} - \dfrac{{14}}{{17}}\\ = \left( {\dfrac{{31}}{{17}} - \dfrac{{14}}{{17}}} \right) + \left( {\dfrac{{ - 5}}{{13}} + \dfrac{{ - 8}}{{13}}} \right)\\ = \dfrac{{17}}{{17}} + \dfrac{{ - 13}}{{13}}\\ = 1 + \left( { - 1} \right)\\\, = 0\end{array}\)

\(\begin{array}{l}b)\,7\dfrac{5}{{11}} - \left( {2\dfrac{3}{7} + 3\dfrac{5}{{11}}} \right)\\ = 7 + \dfrac{5}{{11}} - \left( {2 + \dfrac{3}{7} + 3 + \dfrac{5}{{11}}} \right)\\ = 7 + \dfrac{5}{{11}} - 2 - 3 - \dfrac{3}{7} - \dfrac{5}{{11}}\\ = \left( {7 - 2 - 3} \right) + \left( {\dfrac{5}{{11}} - \dfrac{5}{{11}}} \right) - \dfrac{3}{7}\\ = 2 + 0 - \dfrac{3}{7}\\ = \dfrac{{14}}{7} - \dfrac{3}{7}\\\, = \dfrac{{11}}{7}\end{array}\)

LG bài 2

Phương pháp giải:

a) Chuyển \(\dfrac{1}{2}\) từ vế phải sang vế trái, đổi dấu thành \(\dfrac{{ - 1}}{2}\), rồi thực hiện phép tính \( - \dfrac{3}{4} - \dfrac{1}{2}\) ta tìm được x.

b) Viết \(8 = {2^3}\)\( \Rightarrow x + 3 = 2\) từ đó tìm được x.

c) Chuyển \(\dfrac{{ - 1}}{3}\) sang vế phải đổi dấu thành \( + \dfrac{1}{3}\), rồi thực hiện phép tính \(\dfrac{8}{3} + \dfrac{1}{3}\) từ đó tìm được \(3.\left| x \right| = 3\)

Rồi tìm x.

Lời giải chi tiết:

\(\begin{array}{l}a)\,x + \dfrac{1}{2} = \dfrac{{ - 3}}{4}\\x = \dfrac{{ - 3}}{4} - \dfrac{1}{2}\\x = \dfrac{{ - 5}}{4}\end{array}\)                  

Vậy \(x = \dfrac{{ - 5}}{4}\)     

\(\begin{array}{l}b)\,{\left( {x + 3} \right)^3} = 8\\{\left( {x + 3} \right)^3} = {2^3}\\x + 3 = 2\\x\,\,\,\,\,\,\,\,\, =  - 1\end{array}\)

Vậy \(x =  - 1\)

\(\begin{array}{l}c)\,3.\left| x \right| - \dfrac{1}{3} = \dfrac{8}{3}\\\,\,\,\,3.\left| x \right|\,\,\,\,\,\,\,\,\,\, = \dfrac{8}{3} + \dfrac{1}{3}\\\,\,\,\,3.\left| x \right|\,\,\,\,\,\,\,\,\,\, = 3\\\,\,\,\,\,\,\,\,\left| x \right|\,\,\,\,\,\,\,\,\,\, = 1\\ \Rightarrow x = 1;\,x =  - 1\end{array}\)

Vậy \(x = 1\) hoặc \(x =  - 1\)

LG bài 3

Phương pháp giải:

Muốn tìm \(\dfrac{m}{n}\) của một số \(b\) cho trước, ta tính \(b.\dfrac{m}{n}\,\left( {m,n \in N,\,n \ne 0} \right)\)

Lời giải chi tiết:

a) Số bài kiểm tra đạt loại giỏi là: \(\dfrac{1}{3}.45 = \dfrac{{45}}{3} = 15\) (bài)

Số bài còn lại là: \(45 - 15 = 30\) (bài)

Số bài đạt điểm khá là : \(90\% .30\)\( = \dfrac{{90}}{{100}}.30 = 27\) (bài)

Số bài đạt điểm trung bình là : \(30 - 27 = 3\) (bài)

b) Tỷ số phần trăm số bài đạt điểm trung bình so với tổng số bài kiểm tra là : \(\dfrac{3}{{45}}. 100 \approx 6.7\% \)

Đáp số : a) \(3\) bài     b) \(6,7\% \)

LG bài 4

Phương pháp giải:

a) Chứng minh tia \(Ob\) nằm giữa hai tia \(Oa;\,Oc\)

\( \Rightarrow \angle aOb + \angle bOc = \angle aOc\) \( \Rightarrow \angle bOc\)

b) Chứng minh tia \(Ob\) là tia phân giác góc \(aOc\), ta chỉ ra \(Ob\) nằm giữa hai tia còn lại, và có \(\angle aOb = \angle bOc = {50^0}\)

c) Tính góc \(cOa'\) rồi tính góc \(bOa'\)

d) Chứng minh điểm \(M\) nằm giữa hai điểm \(O\,\) và điểm \(P\) rồi suy ra biểu thức để tính MP

Lời giải chi tiết:

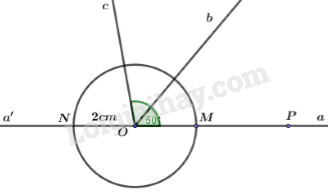
a) Trên nửa mặt phẳng bờ chứa tia Oa, ta có : \(\angle aOb = {50^0} < \angle aOc = {100^o}\)

\( \Rightarrow tia\,Ob\) nằm giữa hai tia \(Oa;\,Oc\)

\(\begin{array}{l} \Rightarrow \angle aOb + \angle bOc = \angle aOc\\ \Rightarrow {50^0}\,\,\,\,\,\,\,\, + \,\angle bOc = {100^0}\\ \Rightarrow \,\,\angle bOc = {100^0} - {50^0}\\ \Rightarrow \,\,\angle bOc = {50^0}\end{array}\)

b) Tia \(Ob\)là tia phân giác của góc \(\angle aOc\) vì:

+ Tia \(Ob\) nằm giữa hai tia \(Oa;\,Oc\)

+ \(\angle aOb = \angle bOc = {50^0}\)

c) Trên nửa mặt phẳng bờ \(aa'\) ta có:

\(\angle aOc = {100^0} < \angle aOa' = {180^0}\)

\( \Rightarrow Tia\,\,Oc\) nằm giữa hai tia \(Oa;\,\,Oa'\)

\(\begin{array}{l} \Rightarrow \angle aOc + \angle cOa' = \angle aOa'\\ \Rightarrow {100^0} + \,\,\,\,\angle cOa' = {180^0}\\ \Rightarrow \,\angle cOa' = {180^0} - {100^0}\\ \Rightarrow \,\angle cOa' = {80^0}\end{array}\)

Trên mặt phẳng bờ chứa tia Ob ta có: \(\angle bOc = {50^0} < \angle cOa' = {80^0}\)

\( \Rightarrow Tia\,\,Oc\) nằm giữa hai tia \(Ob;\,\,Oa'\)

\(\begin{array}{l} \Rightarrow \angle cOa' + \angle bOc = \angle a'Ob\\ \Rightarrow {80^0} + {50^0} = \angle a'Ob = {130^0}\\ \Rightarrow \angle bOa' = {130^0}\end{array}\)

d) Vẽ đường tròn \(\left( {O;2cm} \right)\) cắt đường thẳng \(aa'\) tại hai điểm \(M,N.\) Trên tia \(Oa\) lấy điểm \(P\) sao cho \(OP = 5cm.\) Tính độ dài đoạn thẳng \(MP.\)

\(M \in Oa;\,N \in Oa'\)

Ta có : \(OM = 2cm < OP = 5cm\)

\( \Rightarrow M\) nằm giữa \(O\) và \(P\)

\(\begin{array}{l} \Rightarrow OM + MP = OP\\ \Rightarrow 2\,\,\,\,\,\,\,\, + MP = 5\\ \Rightarrow MP = 5 - 2 = 3\left( {cm} \right)\end{array}\)

LG bài 5

Phương pháp giải:

Chia làm 2 vế để chứng minh. Ta chứng minh \(S > 2\) rồi chứng minh \(S < 5\). Hoặc ngược lại, chứng minh \(S < 5\)rồi chứng minh \(S > 2\).

Ta thấy :

 \(S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + ... + \dfrac{5}{{{{100}^2}}}\)

\( = 5.\left( {\dfrac{1}{{2.2}} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + ... + \dfrac{1}{{100.100}}} \right)\)\( > 5.\left( {\dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \dfrac{1}{{4.5}} + ... + \dfrac{1}{{100.101}}} \right)\)

Rồi sử dụng : \(\dfrac{1}{{n.\left( {n + 1} \right)}} = \dfrac{1}{n} - \dfrac{1}{{n + 1}}\) để thu gọn S rồi so sánh S với 2.

Tương tự khi so sánh S với 5.

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + ... + \dfrac{5}{{{{100}^2}}}.\\ = 5.\left( {\dfrac{1}{{2.2}} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + ... + \dfrac{1}{{100.100}}} \right)\\ > 5.\left( {\dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \dfrac{1}{{4.5}} + ... + \dfrac{1}{{100.101}}} \right)\\ > 5.\left( {\dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{{100}} - \dfrac{1}{{101}}} \right)\\ > 5.\left( {\dfrac{1}{2} - \dfrac{1}{{101}}} \right) > \dfrac{5}{2} > 2\\ \Rightarrow S > 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\end{array}\)

\(\begin{array}{l}S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + ... + \dfrac{5}{{{{100}^2}}}.\\ = 5.\left( {\dfrac{1}{{2.2}} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + ... + \dfrac{1}{{100.100}}} \right)\\ < 5.\left( {\dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{99.100}}} \right)\\ < 5.\left( {1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{{99}} - \dfrac{1}{{100}}} \right)\\ < 5.\left( {1 - \dfrac{1}{{100}}} \right) < 5\\ \Rightarrow S < 5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array}\)

Từ (1) và (2) : \(2 < S < 5\) (đpcm).

Nguồn sưu tầm

Loigiaihay.com