Đề số 1 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10Đáp án và lời giải chi tiết Đề số 1 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán học 10 Quảng cáo
Đề bài Bài 1. (3 điểm) 1. Giải các bất phương trình sau : a) \(\left( {1 - 2x} \right)\left( {{x^2} - x - 20} \right) > 0\) b) \(\sqrt {{x^2} - x - 2} < x - 1.\) 2. Tìm tất cả các giá trị của tham số \(m\) để biểu thức \(f\left( x \right) = {x^2} - 2\left( {m - 1} \right)x - {m^2} + m + 6\) luôn dương với mọi \(x.\) Bài 2. (2,5 điểm)
Bài 3. (4 điểm)
a) Tìm tọa độ tâm \(I\) và bán kính \(R\) của đường tròn \(\left( C \right).\) Chứng tỏ điểm \(A\) nằm ngoài đường tròn \(\left( C \right)\). b) Viết phương trình đường thẳng \(\left( d \right)\) đi qua điểm \(A\) và song song với đường thẳng \(\left( \Delta \right)\). c) Tìm tọa độ điểm \(M\) thuộc đường thẳng \(\left( \Delta \right)\) sao cho \(IM = 2R,\) (trong đó \(I,R\) lần lượt là tâm và bán kính của đường tròn \(\left( C \right)\)). Bài 4. (0,5 điểm) Giải bất phương trình sau: \(\sqrt {{x^2} + 4x} + 2\sqrt {x - 2} \ge \sqrt {2{x^2} + 12x - 8} .\) Lời giải chi tiết Bài 1 (VD) Phương pháp: 1a: Đưa về bất phương trình tích rồi lập bảng xét dấu để tìm nghiệm của bất phương trình. 1b: \(\sqrt A < B \Leftrightarrow \left\{ \begin{array}{l}A \ge 0\\B > 0\\A < {B^2}\end{array} \right..\) 2: Xét dấu của tam thức bậc hai: \(a{x^2} + bx + c > 0\left( {a \ne 0} \right) \forall x \\ \Leftrightarrow \left\{ \begin{array}{l}\Delta < 0\\a > 0\end{array} \right..\) Cách giải: 1. Giải các bất phương trình sau: a) \(\left( {1 - 2x} \right)\left( {{x^2} - x - 20} \right) > 0\)\( \Leftrightarrow \left( {1 - 2x} \right)\left( {x + 4} \right)\left( {x - 5} \right) > 0\) Xét \(f\left( x \right) = \left( {1 - 2x} \right)\left( {x + 4} \right)\left( {x - 5} \right) = 0 \) \(\Leftrightarrow \left[ \begin{array}{l}x = \frac{1}{2}\\x = - 4\\x = 5\end{array} \right.\) Ta có bảng xét dấu :
Vậy tập nghiệm của bất phương trình là \(S = \left( { - \infty ; - 4} \right) \cup \left( {\frac{1}{2};5} \right)\). b) \(\sqrt {{x^2} - x - 2} < x - 1 \) \(\Leftrightarrow \left\{ \begin{array}{l}{x^2} - x - 2 \ge 0\\x - 1 > 0\\{x^2} - x - 2 < {x^2} - 2x + 1\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 2} \right)\left( {x + 1} \right) \ge 0\\x > 1\\x < 3\end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x \ge 2\\x \le - 1\end{array} \right.\\x > 1\\x < 3\end{array} \right. \Leftrightarrow 2 \le x < 3.\) 2. Tìm tất cả các giá trị của tham số \(m\) để biểu thức \(f\left( x \right) = {x^2} - 2\left( {m - 1} \right)x\)\( - {m^2} + m + 6\) luôn dương với mọi \(x.\) \(\begin{array}{l}f\left( x \right) = {x^2} - 2\left( {m - 1} \right)x - {m^2} + m \\+ 6 > 0,\,\forall x\\ \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = {\left( {m - 1} \right)^2} \\- 1\left( { - {m^2} + m + 6} \right) < 0\\1 > 0\end{array} \right.\\ \Leftrightarrow 2{m^2} - 3m - 5 < 0\\ \Leftrightarrow \left( {m + 1} \right)\left( {2m - 5} \right) < 0\\ \Leftrightarrow - 1 < m < \frac{5}{2}.\end{array}\) Vậy \( - 1 < m < \frac{5}{2}\). Bài 2 (VD) Phương pháp: 1. Với \(\frac{\pi }{2} < \alpha < \pi \) ta có: \(\sin \alpha > 0,\,\,\,\cos \alpha < 0.\) 2. Sử dụng công thức \(\cos 2a = 2{\cos ^2}a - 1.\) Cách giải: 1. Cho \(\sin \alpha = \frac{5}{{13}}\) và \(\frac{\pi }{2} < \alpha < \pi .\) Tính giá trị biểu thức \(A = 3\cos \alpha + 2\sin \alpha .\) Với \(\frac{\pi }{2} < \alpha < \pi \) thì \(\cos \alpha < 0.\) Ta có: \(\left| {\cos \alpha } \right| = \sqrt {1 - {{\sin }^2}\alpha } = \sqrt {1 - {{\left( {\frac{5}{{13}}} \right)}^2}}\)\( = \frac{{12}}{{13}},\) mà \(\cos \alpha < 0\) nên \(\cos \alpha = - \frac{{12}}{{13}}.\) \( \Rightarrow A = 3\cos \alpha + 2\sin \alpha \\ = 3.\left( { - \frac{{12}}{{13}}} \right) + 2.\frac{5}{{13}} = - 2.\) 2. Chứng minh rằng \(\sqrt {\frac{1}{2} + \frac{1}{2}\sqrt {\frac{1}{2} + \frac{1}{2}\cos x} } = \cos \frac{x}{4}\) (với \(0 < x < \frac{\pi }{2}\)). Với \(0 < x < \frac{\pi }{2}\) thì \(\cos \frac{x}{2} > 0,\,\,\,\cos \frac{x}{4} > 0.\) \(VT = \sqrt {\frac{1}{2} + \frac{1}{2}\sqrt {\frac{1}{2} + \frac{1}{2}\cos x} } \\= \sqrt {\frac{1}{2} + \frac{1}{2}\sqrt {\frac{{\cos x + 1}}{2}} } \)\( = \sqrt {\frac{1}{2} + \frac{1}{2}\sqrt {\frac{{\left( {2{{\cos }^2}\frac{x}{2} - 1} \right) + 1}}{2}} } \\ = \sqrt {\frac{1}{2} + \frac{1}{2}\cos \frac{x}{2}} \) \( = \sqrt {\frac{{\cos \frac{x}{2} + 1}}{2}} = \sqrt {\frac{{\left( {2{{\cos }^2}\frac{x}{4} - 1} \right) + 1}}{2}}\\ = \cos \frac{x}{4}.\) Vậy \(\sqrt {\frac{1}{2} + \frac{1}{2}\sqrt {\frac{1}{2} + \frac{1}{2}\cos x} } = \cos \frac{x}{4}\) với \(0 < x < \frac{\pi }{2}.\) Bài 3 (VD) Phương pháp: 1. Áp dụng định lý hàm số sin và định lý hàm số cos trong tam giác. 2. a) Đường tròn tâm \(I\left( {a;b} \right)\) bán kính \(R\) có phương trình: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}.\) Nếu \(IA > R\) thì điểm \(A\) nằm ngoài đường tròn \(\left( C \right).\) b) Hai đường thẳng song song với nhau thì có cùng véc-tơ pháp tuyến. Phương trình đường thẳng \(d\) đi qua \(M\left( {{x_0};\,\,{y_0}} \right)\) và có VTPT \(\overrightarrow n = \left( {A;\,\,B} \right)\) có dạng: \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) = 0.\) c) Lập phương trình \(IM = 2R\) theo tọa độ của \(M\) và giải phương trình. Cách giải: 1. Cho tam giác \(ABC\) có \(AB = 6,AC = 8\) và \(\angle BAC = 60^\circ .\) Tính bán kính đường tròn ngoại tiếp tam giác \(ABC\). Áp dụng định lý cos trong tam giác \(ABC\) ta có: \(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} \\- 2AB.AC\cos \angle BAC\\B{C^2} = {6^2} + {8^2} - 2.6.8.\cos {60^0}\\BC = 2\sqrt {13} .\end{array}\) Áp dụng định lý hàm số sin trong tam giác \(ABC\) ta có: \(\frac{{BC}}{{\sin \angle BAC}} = 2R\) (trong đó \(R\) là bán kính đường tròn ngoại tiếp tam giác \(BAC\)). \( \Rightarrow \frac{{2\sqrt {13} }}{{\sin {{60}^0}}} = 2R \Rightarrow R = \frac{{2\sqrt {39} }}{3}.\) 2. Trong mặt phẳng tọa độ \(Oxy,\) cho điểm \(A\left( {1; - 3} \right)\), đường thẳng \(\left( \Delta \right):2x - y + 3 = 0\) và đường tròn \(\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 25.\) a) Tìm tọa độ tâm \(I\) và bán kính \(R\) của đường tròn \(\left( C \right).\) Chứng tỏ điểm \(A\) nằm ngoài đường tròn \(\left( C \right)\). \(\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 25\) có tâm \(I\left( {2;\,\,3} \right)\) và bán kính \(R = 5.\) Có \(AI = \sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( {3 + 3} \right)}^2}} = \sqrt {37} > R\) nên \(A\) nằm ngoài đường tròn \(\left( C \right).\) b) Viết phương trình đường thẳng \(\left( d \right)\) đi qua điểm \(A\) và song song với đường thẳng \(\left( \Delta \right)\). Đường thẳng \(\left( d \right)\) song song với đường thẳng \(\left( \Delta \right):2x - y + 3 = 0\) nên \(\left( d \right)\) có VTPT là \(\overrightarrow n \left( {2; - 1} \right).\) Đường thẳng \(\left( d \right)\) đi qua điểm \(A\left( {1; - 3} \right)\) và có VTPT là \(\overrightarrow n \left( {2; - 1} \right)\) nên \(\left( d \right)\) có phương trình là: \(2\left( {x - 1} \right) - \left( {y + 3} \right) = 0 \)\(\Leftrightarrow 2x - y - 5 = 0.\) Vậy \(\left( d \right):2x - y - 5 = 0.\) c) Tìm tọa độ điểm \(M\) thuộc đường thẳng \(\left( \Delta \right)\) sao cho \(IM = 2R,\) (trong đó \(I,R\) lần lượt là tâm và bán kính của đường tròn \(\left( C \right)\)). Vì \(M\) thuộc đường thẳng \(\left( \Delta \right)\) nên gọi \(M\left( {a;\,\,2a + 3} \right).\) \(\begin{array}{l} \Rightarrow IM = 2R\\ \Leftrightarrow \sqrt {{{\left( {a - 2} \right)}^2} + {{\left( {2a + 3 - 3} \right)}^2}} = 10\\ \Leftrightarrow \sqrt {{a^2} - 4a + 4 + 4{a^2}} = 10\\ \Leftrightarrow 5{a^2} - 4a + 4 = 100\\ \Leftrightarrow \left[ \begin{array}{l}a = \frac{{24}}{5} \Rightarrow M\left( {\frac{{24}}{5};\frac{{63}}{5}} \right)\\a = - 4 \Rightarrow M\left( { - 4; - 5} \right)\end{array} \right..\end{array}\) Vậy \(M\left( {\frac{{24}}{5};\frac{{63}}{5}} \right)\) hoặc \(M\left( { - 4; - 5} \right)\) thỏa mãn yêu cầu. Bài 4 (VDC) Phương pháp: Giải bất phương trình bằng phương pháp đặt ẩn phụ. Cách giải: \(\sqrt {{x^2} + 4x} + 2\sqrt {x - 2} \\ \ge \sqrt {2{x^2} + 12x - 8} \,\,\left( * \right)\) Điều kiện: \(x \ge 2.\) Đặt \(\left\{ \begin{array}{l}\sqrt {{x^2} + 4x} = a\\2\sqrt {x - 2} = b\,\,\end{array} \right..\) Với \(x \ge 2\) thì \(a > 0,\,\,b \ge 0.\) Ta có: \(2{x^2} + 12x - 8 = 2\left( {{x^2} + 4x} \right) \)\(+ 4\left( {x - 2} \right) = 2{a^2} + {b^2}.\) \(\begin{array}{l} \Rightarrow \left( * \right) \Leftrightarrow a + b \ge \sqrt {2{a^2} + {b^2}} \\ \Leftrightarrow {a^2} + 2ab + {b^2} \ge 2{a^2} + {b^2}\\ \Leftrightarrow 2ab \ge {a^2}\\ \Leftrightarrow 2b \ge a\,\,\,\,\,\left( {do\,\,\,a > 0} \right)\\ \Leftrightarrow 4\sqrt {x - 2} \ge \sqrt {{x^2} + 4x} \\ \Leftrightarrow 16\left( {x - 2} \right) \ge {x^2} + 4x\\ \Leftrightarrow {x^2} - 12x + 32 \le 0\\ \Leftrightarrow \left( {x - 4} \right)\left( {x - 8} \right) \le 0\\ \Leftrightarrow 4 \le x \le 8.\end{array}\) Kết hợp với điều kiện ta có \(4 \le x \le 8\) là tập nghiệm của bất phương trình. Nguồn: Sưu tầm Loigiaihay.com
|














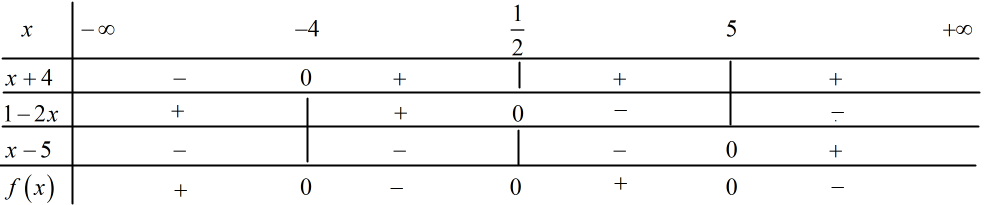






Danh sách bình luận