Đề số 3 - Đề kiểm tra học kì 2 - Vật lí 12

Đề bài

Câu 13: Trong thí nghiệm Young về giao thoa với ánh sáng đơn sắc, khoảng cách giữa hai khe là 1 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 2m. Bề rộng 6 vân sáng liên tiếp đo được là 4,8mm. Tần số ánh sáng đơn sắc dùng trong thí nghiệm l

A. 7,5.10¹⁴ Hz.                   B. 6,25.10⁸ Hz

C. 6,25.10¹⁴ Hz                  D. 7,5.10⁸ Hz

Câu 14: Poloni \(_{84}^{210}Po\) phóng xạ α và biến đổi thành chì \({}_{82}^{206}Pb\) . Chu kỳ bán rã là 138 ngày. Cho rằng toàn bộ hạt nhân chì sinh ra trong quá trình phân rã đều có trong mẫu chất. Tại thời điểm t₁ tỉ số giữa hạt nhân Poloni và hạt nhân chì có trong mẫu là \(\frac{1}{7}\) , tại thời điểm \({t_2} = {t_1} + \Delta t\) thì tỉ số đó là \(\frac{1}{{31}}\) . Khoảng thời gian ∆t là:

A. 267 ngày                            B.  138 ngày

C. 414 ngày                            D.  69 ngày.

Câu 15: Công dụng nào sau đây không phải của tia tử ngoại?

A. Chữa bệnh còi xương.

B. Tìm vết nứt trên bề mặt các vật bằng kim loại.

C. Được ứng dụng trong các bộ điều khiển từ xa của tivi, quạt, máy lạnh.

D. Dùng để tiệt trùng thực phẩm trước khi đóng gói hoặc đóng hộp.

Câu 16: Trong thí nghiệm Young về giao thoa ánh sáng, hai khe được chiếu sáng bằng ánh sáng gồm hai ánh sáng đơn sắc có bước sóng λ₁ = 0,6µm và λ₂ = 0,4µm. Trên màn quan sát, trong khoảng giữa hai vân sáng bậc 7 của bức xạ có bước sóng λ₁, số vân sáng trùng nhau của hai bức xạ là

A. 7                 B. 6     

C. 8                 D. 5

Câu 17: Khi nói về phôtôn, phát biểu nào dưới đây là đúng?

A. Với mỗi ánh sáng đơn sắc có tần số f, các phôtôn đều mang năng lượng như nhau.

B. Năng lượng của phôtôn càng lớn khi bước sóng ánh sáng ứng với phôtôn đó càng lớn.

C. Năng lượng của phôtôn ánh sáng tím nhỏ hơn năng lượng của phôtôn ánh sáng đỏ.

D. Phôtôn có thể tồn tại trong trạng thái đứng yên.

Câu 18: Hiệu điện thế giữa anốt và catốt của một ống Rơnghen là U = 30kV. Xem như vận tốc ban đầu của chùm êlectrôn phát ra từ catốt bằng không. Tần số lớn nhất của tia Rơnghen do ống này phát ra có thể là

A. 60,38.10¹⁸ Hz.          B. 7,25.10¹⁸ Hz.

C. 60,38.10¹⁵ Hz.          D. 7,25.10¹⁵ Hz.

Câu 19: Trong thí nghiệm Young về giao thoa ánh sáng, khoảng cách hai khe là 0,4mm, khoảng cách từ hai khe đến màn là 1m, bước sóng ánh sáng đơn sắc là 0,64µm. Tại điểm M cách vân trung tâm 5,6mm là

A. vân sáng bậc 4       B. vân tối thứ 3 

C. vân tối thứ 4          D. vân sáng bậc 3

Câu 20: Trong thí nghiệm Young về giao thoa ánh sáng, nguồn S phát ra đồng thời ba bức xạ đơn sắc có bước sóng lần lượt là 0,4µm; 0,5µm và 0,6µm. Trên màn, trong khoảng giữa hai vân sáng liên tiếp cùng màu với vân sáng trung tâm, số vị trí mà ở đó chỉ có một bức xạ cho vân sáng?

A. 22.                                     B. 20. 

C. 30.                                     D. 27.

Câu 21: Một nguồn sáng chỉ phát ra ánh sáng đơn sắc có tần số 7,5.10¹⁴ Hz. Công suất bức xạ điện từ của nguồn là 0,4W. Số phôtôn mà nguồn phát ra trong một giây xấp xỉ bằng

A. 3,02.10¹⁹ photon.                                

B. 0,33.10¹⁹ photon.

C. 8,05.10¹⁷ photon.                                

D. 3,24.10¹⁹ photon.

Câu 22: Theo mẫu Bohr về nguyên tử hiđrô, nếu lực tương tác tĩnh điện giữa êlectron và hạt nhân khi êlectron chuyển động trên quỹ đạo dừng K là F thì khi êlectron chuyển động trên quỹ đạo dừng M, lực này sẽ là

A. \(\frac{F}{{16}}\)              B. \(\frac{F}{9}\)                   

C. \(\frac{F}{{81}}\)               D. \(\frac{F}{{25}}\)

Câu 23: Một chất phóng xạ có chu kì bán rã là 3,8 ngày. Số hạt nhân sẽ bị phân rã hết 70% sau thời gian là

A. 6,6 ngày.                            B. 7,6 ngày. 

C. 4,8 ngày.                            D. 8,8 ngày.

Câu 24: Khối lượng của hạt nhân \({}_4^{10}Be\) là 10,0113u. Độ hụt khối của hạt nhân \({}_4^{10}Be\) là

A. 0,9110u.                            B. 0,0701u.

C. 0,0561u.                            D. 0,0811u.

B – TỰ LUẬN (4 ĐIỂM)

Học sinh trình bày theo hình thức tự luận (ghi công thức, lập luận, giải thích...) các câu sau: câu 3, câu 6, câu 13, câu 14, câu 21, câu 23.

Lời giải chi tiết

1.B	2.B	3.C	4.D	5.D	6.C
7.B	8.D	9.D	10.B	11.C	12.B
13.C	14.A	15.C	16.D	17.A	18.B
19.C	20.B	21.C	22.C	23.A	24.B

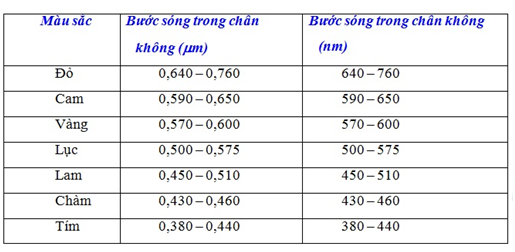
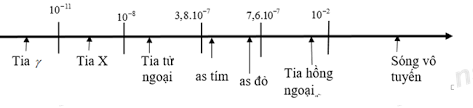
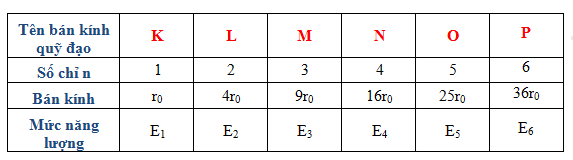
Câu 1:

Phương pháp:

Năng lượng các trạng thái dừng của nguyên tử hyđro tính theo công thức:

\({E_n} = \frac{{ - 13,6}}{{{n^2}}}eV;\,\,\,\,n = 1,2,3 \ldots \)

Bán kính quỹ đạo xác định theo công thức: \({r_n} = {n^2}.{r_0}\)

Khi chuyển từ mức năng lượng này sang mức năng lượng khác thì nguyên tử phát ra một photon có năng lượng thỏa mãn: \(\varepsilon  = \frac{{hc}}{\lambda } = {E_m} - {E_n}\)

Cách giải:

Nguyên tử hyđro đang ở trạng thái cơ bản, khi nhận được năng lượng kích thích thì bán kính quỹ đạo của electron tăng lên 16 lần, tức là:

 \({r_n} = {n^2}.{r_0} = 16{r_0} \Rightarrow n = 4\)

Khi chuyển từ mức năng lượng này sang mức năng lượng khác thì nguyên tử phát ra một photon có năng lượng thỏa mãn:

\(\begin{array}{l}\varepsilon  = \frac{{hc}}{\lambda } = {E_n} - {E_0} = \frac{{ - 13,6}}{{16}} - ( - 13,6) = 12,75eV = 20,{4.10^{ - 19}}J\\ \Rightarrow \lambda  = \frac{{hc}}{\varepsilon } = \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{20,{{4.10}^{ - 19}}}} = 0,{974.10^{ - 7}}m = 0,0974\mu m\end{array}\)

Chọn B.

Câu 2:

Phương pháp:

Công thức khoảng vân \(i = \frac{{\lambda D}}{a}\) 

Cách giải:

Công thức khoảng vân: \(i = \frac{{\lambda D}}{a} \Rightarrow i \sim \lambda \)

Bảng bước sóng ánh sáng:

 

Nếu thay ánh sáng đơn sắc màu lục bằng ánh sáng đơn sắc màu vàng và giữ nguyên các điều kiện khác thì bước sóng tăng lên, nên khoảng vân tăng.

Chọn B. 

Câu 3:

Phương pháp:

Vị trí vân sáng: \({x_s} = k.i = k.\frac{{\lambda D}}{a};k \in Z\)

Cách giải:

Toạ độ của vân sáng bậc 5 là: \({x_{s5}} = 5.i\)

Khoảng cách từ vân sáng bậc 5 đến vân sáng bậc 5 ở hai phía vân trung tâm là:

\(d = 5i + 5i = 10i = 10.\frac{{\lambda D}}{a} = 10.\frac{{0,6.2}}{1} = {12_{}}mm\)

Chọn C.

Câu 4:

Phương pháp:

Sử dụng bảng thang sóng điện từ

Cách giải:

Sử dụng bảng thang sóng điện từ

 

Thứ tự bước sóng giảm dần là: sóng vô tuyến, tia hồng ngoại, ánh sáng thấy được, tia X, tia gamma.

Chọn D.

Câu 5:

Phương pháp:

Bán kính quỹ đạo dừng xác định theo công thức: \({r_n} = {n^2}.{r_0};\,\,\,n = 1,2,3,...\)

Cách giải:

Bán kính quỹ đạo xác định theo công thức:

\({r_n} = {n^2}.{r_0};\,\,\,n = 1,2,3,...\)

→ Vì vậy không thể có bán kĩnh quỹ đạo: \({r_n} = 8{r_0}\)

Chọn D.

Câu 6:

Phương pháp:

Giới hạn quang điện:\({\lambda _0} = \frac{{hc}}{A}\)

Đổi đơn vị \(1eV = 1,{6.10^{ - 19}}J\)

Cách giải:

Đổi đơn vị \(1eV = 1,{6.10^{ - 19}}J\)

Giới hạn quang điện của kim loại này là:

\({\lambda _0} = \dfrac{{hc}}{A} = \dfrac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{4,14.1,{{6.10}^{ - 19}}}} = 3,{0.10^{ - 7}} = 0,3\mu m\)

Chọn C.

Câu 7:

Phương pháp:

Quang phổ liên tục:

+ Nguồn phát: Các chất rắn, chất lỏng và chất khí có áp suất lớn khi bị nung nóng sẽ phát ra quang phổ liên tục.

+ Đặc điểm: Quang phổ liên tục không phụ thuộc vào bản chất của vật phát sáng mà chỉ phụ thuộc nhiệt độ.

Cách giải:

Đặc điểm quan trọng của quang phổ liên tục là không phụ thuộc vào thành phần cấu tạo mà chỉ phụ thuộc vào nhiệt độ của nguồn sáng.

Chọn B.

Câu 8:

Phương pháp:

Áp dụng định luật bảo toàn số khối và bảo toàn điện tích để viết phương trình phản ứng hạt nhân.

Tìm số hạt nhân ban đầu: \({N_0} = \frac{m}{A}.{N_A}\)

Số hạt nhân mẹ còn lại sau thời gian t được xác định bởi: \(N = {N_0}{.2^{\frac{{ - t}}{T}}}\)

Số hạt nhân con được tạo thành sau thời gian t được xác định bởi:\(N' = {N_0} - N = {N_0}.(1 - {2^{\frac{{ - t}}{T}}})\)

Cách giải:

Phương trình phóng xạ:  \({}_{11}^{24}Na \to {}_{ - 1}^0e + {}_{12}^{24}Mg\)

Số hạt nhân ban đầu: \({N_0} = \frac{m}{A}.{N_A} = \frac{{12}}{{24}}.6,{023.10^{23}} = 3,{0115.10^{23}}\)

Số hạt nhân con được tạo thành sau thời gian t = 3T:

\(N' = {N_0} - N = {N_0}.(1 - {2^{\frac{{ - t}}{T}}}) = 3,{0115.10^{23}}.\left( {1 - {2^{\frac{{ - 3T}}{T}}}} \right) = 2,{626.10^{23}}\)

Chọn D. 

Câu 9:

Phương pháp:

Sử dụng lý thuyết về phản ứng phân hạch và nhiệt hạch

Cách giải:

Phản ứng phân hạch là sự vỡ của một hạt nhân nặng thành hai hạt nhân trung bình (kèm theo một vài nơtron). Phân hạch là phản ứng tỏa năng lượng, phản ứng phân hạc có dây chuyển có thể điều khiển được tạo ra trong lò phản ứng hạt nhân.

Phản ưng nhiệt hạch là sự tổng hợp hai hay nhiều hạt nhân nhẹ thành một hạt nhân nặng hơn. Phản ứng xảy ra ở nhiệt độ cao và tỏa ra năng lượng rất lớn, là phản ứng không điều khiển được.

→ Điểm giống nhau của phản ứng phân hạch và nhiệt hạch là các phản ứng tỏa năng lượng (nhiệt).

Chọn D.

Câu 10:

Phương pháp:

Sử dụng lý thuyết về các dạng phóng xạ.

Cách giải:

Các dạng phóng xạ :

+ phóng xạ α: \({}_Z^AX \to {}_2^4He + {}_{Z - 2}^{A - 4}Y\)

+ Phóng xạ β⁺: \({}_Z^AX \to {}_{Z - 1}^AY + {}_{ + 1}^0e\)

+ phóng xạ β^-: \({}_Z^AX \to {}_{Z + 1}^AY + {}_{ - 1}^0e\)

+ Phóng xạ γ: không biến đổi hạt nhân, nó xuất hiện trong các phóng xạ β⁺ hoặc β^- khi hạt nhân con ở trạng thái kích thích.

Chọn B.

Câu 11:

Phương pháp:

Tia laze có tính đơn sắc, tính định hướng và tính kết hợp rất cao và cường độ lớn.

Cách giải:

Tia laze có tính đơn sắc, tính định hướng và tính kết hợp rất cao và cường độ lớn.

Trong công nghiệp, vì tia laze có cường độ lớn và tính định hướng cao nên nó được dùng trong các công việc như cắt, khoan, tôi... chính xác.

Chọn C.

Câu 12:

Phương pháp:

Sử dụng định luật bảo toàn điện tích và bảo toàn nuclon để viết phương trình phản ứng hạt nhân.

Cách giải:

Sử dụng định luật bảo toàn điện tích và bảo toàn nuclon ta có phương trình phản ứng:

\({}_3^6Li + {}_1^2H \to {}_4^7Be + {}_0^1n\)

→ Vậy hạt nhân X là: \({}_1^2H\)

Chọn B.

Câu 13:

Phương pháp:

Khoảng vân i là khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp.

Áp dụng công thức tính khoảng vân \(i = \frac{{\lambda D}}{a}\)

Công thức tính tần số ánh sáng \(f = \frac{c}{\lambda }\)

Cách giải:

Bề rộng 6 vân sáng ứng với 5 khoảng vân. Nên ta có:

\(5i = 4,8mm \Rightarrow i = \frac{{4,8}}{5} = 0,96mm\)

Lại có: \(i = \frac{{\lambda D}}{a} \Rightarrow \lambda  = \frac{{ia}}{D} = \frac{{0,96.1}}{2} = 0,48\mu m\)

→ Tần số ánh sáng: \(f = \frac{c}{\lambda } = \frac{{{{3.10}^8}}}{{0,{{48.10}^{ - 6}}}} = 6,{25.10^{14}}Hz\)

Chọn C.

Câu 14:

Phương pháp:

Viết phương trình phóng xạ.

Số hạt nhân mẹ còn lại sau thời gian t được xác định bởi: \(N = {N_0}{.2^{\dfrac{{ - t}}{T}}}\)

Số hạt nhân con được tạo thành sau thời gian t được xác định bởi: \(N' = {N_0} - N = {N_0}.(1 - {2^{\dfrac{{ - t}}{T}}})\)

Cách giải:

Phương trình phóng xạ: \({}_{84}^{210}Po \to {}_{82}^{206}Pb + {}_2^4He\)

Số hạt nhân mẹ còn lại sau thời gian t được xác định bởi: \(N = {N_0}{.2^{\dfrac{{ - t}}{T}}}\)

Số hạt nhân con được tạo thành sau thời gian t được xác định bởi:

\(N' = {N_0} - N = {N_0}.(1 - {2^{\dfrac{{ - t}}{T}}})\)

Tại thời điểm t₁ tỉ số giữa hạt nhân Poloni và hạt nhân chì có trong mẫu là \(\dfrac{1}{7}\) ta có:

\(\dfrac{{{N_{Po}}}}{{{N_{Pb}}}} = \dfrac{{{2^{\dfrac{{ - {t_1}}}{T}}}}}{{1 - {2^{\dfrac{{ - {t_1}}}{T}}}}} = \dfrac{1}{7} \Rightarrow {t_1} = 3T\)

Tại thời điểm \[{t_2} = {t_1} + \Delta t\]thì tỉ số đó là \(\dfrac{1}{{31}}\)ta có :

\(\begin{array}{l}\dfrac{{{N_{Po}}}}{{{N_{Pb}}}} = \dfrac{{{2^{\dfrac{{ - ({t_1} + \Delta t)}}{T}}}}}{{1 - {2^{^{\dfrac{{ - ({t_1} + \Delta t)}}{T}}}}}} = \dfrac{1}{{31}} \Rightarrow \dfrac{{{2^{\dfrac{{ - {t_1}}}{T}}}{{.2}^{\dfrac{{ - \Delta t}}{T}}}}}{{1 - {2^{\dfrac{{ - {t_1}}}{T}}}{{.2}^{\dfrac{{ - \Delta t}}{T}}}}} = \dfrac{{{2^{ - 3}}{{.2}^{\dfrac{{ - \Delta t}}{T}}}}}{{1 - {2^{ - 3}}{{.2}^{\dfrac{{ - \Delta t}}{T}}}}} = \dfrac{1}{{31}}\\ \Rightarrow {31.2^{ - 3}}{.2^{\dfrac{{ - \Delta t}}{T}}} = 1 - {2^{ - 3}}{.2^{\dfrac{{ - \Delta t}}{T}}} \Rightarrow {32.2^{ - 3}}{.2^{\dfrac{{ - \Delta t}}{T}}} = 1\\ \Rightarrow {2^{\dfrac{{ - \Delta t}}{T}}} = \dfrac{1}{4} = {2^{ - 2}} \Rightarrow \Delta t = 2T = 276\,\,\left( {ngay} \right)\end{array}\)

Chọn A.

Câu 15:

Phương pháp:

Công dụng của tia tử ngoại:

+ Tiệt trùng dụng cụ y tế, chữa bệnh còi xương.

+ Tiệt trùng thực phẩm đóng hộp.

+ Tìm vết nứt trên bề mặt kim loại

Cách giải:

Công dụng của tia tử ngoại:

+ Tiệt trùng dụng cụ y tế, chữa bệnh còi xương.

+ Tiệt trùng thực phẩm đóng hộp.

+ Tìm vết nứt trên bề mặt kim loại.

→ Tia tử ngoại không được dùng để ứng dụng trong các bộ điều khiển từ xa của tivi, quạt, máy lạnh.

Chọn C.

Câu 16:

Phương pháp:

Khoảng vân: \(i = \frac{{\lambda D}}{a}\)

Vì hai ánh sáng cùng cho các vân sáng, nên vị trí hai vân sáng trùng nhau thỏa mãn :\(x = k.\frac{{{\lambda _1}.D}}{a} = k'.\frac{{{\lambda _2}.D}}{a} \Rightarrow \frac{i}{{i'}} = \frac{{{\lambda _1}}}{{{\lambda _2}}} = \frac{{k'}}{k}\)

Khi tỉ số là phân số tối giản thì ta có khoảng vân trùng.

Vân sáng bậc 7 của bức xạ λ₁ có vị trí: x_s7 = 7i₁

Cách giải:

Áp dụng công thức tính khoảng vân \(i = \frac{{\lambda D}}{a}\)

Vì hai ánh sáng cùng cho các vân sáng, nên vị trí hai vân sáng trùng nhau thỏa mãn :

\(\begin{array}{l}x = k.\frac{{{\lambda _1}.D}}{a} = k'.\frac{{{\lambda _2}.D}}{a} \Rightarrow \frac{{{i_1}}}{{{i_2}}} = \frac{{{\lambda _1}}}{{{\lambda _2}}} = \frac{{k'}}{k}\\ \Rightarrow \frac{i}{{i'}} = \frac{{0,4}}{{0,6}} = \frac{2}{3} \Rightarrow {i_{tr}} = 2{i_2} = 3{i_1}\end{array}\)

Vân sáng bậc 7 của bức xạ λ₁ có vị trí: x_s7 = 7i₁

Vậy trong khoảng này có các cặp trùng nhau là: 

\(\left( {0;0} \right);\left( { \pm 2{i_2}; \pm 3{i_1}} \right);\left( { \pm 4{i_2}; \pm 6{i_1}} \right)\)

Vậy có 5 vân trùng nhau.

Chọn D.

Câu 17:

Phương pháp:

Sử dụng thuyết lượng tử ánh sáng

Cách giải :

Thuyết lượng tử ánh sáng

+ Chùm ánh sáng là chùm các phôtôn (các lượng tử ánh sáng). Mỗi phôtôn có năng lượng xác định (năng lượng của 1 phô tôn:

+ Cường độ chùm sáng tỉ lệ với số phôtôn phát ra trong 1 giây.

+ Phân tử, nguyên tử, electron… phát xạ hay hấp thụ ánh sáng,  nghĩa là chúng phát xạ hay hấp thụ phôtôn.

+ Các phôtôn bay dọc theo tia sáng với tốc độ c = 3.10⁸ m/s trong chân không.

+ Năng lượng của mỗi phôtôn rất nhỏ. Một chùm sáng dù yếu cũng chứa rất nhiều phôtôn do rất nhiều nguyên tử, phân tử phát ra. Vì vậy ta nhìn thấy chùm sáng liên tục.

+ Phôtôn chỉ tồn tại trong trạng thái chuyển động. Không có phôtôn đứng yên.

→ Phát biểu đúng là: Với mỗi ánh sáng đơn sắc có tần số f, các phôtôn đều mang năng lượng như nhau

Chọn A.

Câu 18:

Phương pháp:

Hiệu điện thế giữa Anot và Katot gia tốc cho electron, coi vận tốc đầu bằng 0, nên đến khi electron đập vào atot thì nó có năng lượng: \[{{\rm{W}}_d} = \frac{1}{2}m.v_{\max }^2 = eU\]

Khi toàn bộ năng lượng này khi đập vào atot làm nó phát ra tia X có năng lượng lớn nhất ta có:

\(hf = \frac{1}{2}.m.v_{\max }^2 = eU \Rightarrow f = \frac{{eU}}{h}\)

Cách giải:

Hiệu điện thế giữa Anot và Katot gia tốc cho electron, coi vận tốc đầu bằng 0, nên đến khi electron đập vào atot thì nó có năng lượng:

\[{{\rm{W}}_d} = \frac{1}{2}m.v_{\max }^2 = eU\]

Khi toàn bộ năng lượng này khi đập vào atot làm nó phát ra tia X có năng lượng lớn nhất ta có:

\(\begin{array}{l}hf = \frac{1}{2}.m.v_{\max }^2 = eU\\ \Rightarrow f = \frac{{eU}}{h} = \frac{{1,{{6.10}^{ - 19}}{{.30.10}^3}}}{{6,{{625.10}^{ - 34}}}} = 7,{245.10^{18}}Hz\end{array}\)

Chọn B.

Câu 19:

Phương pháp:

Khoảng vân: \(i = \frac{{\lambda D}}{a}\)

Vị trí vân sáng và vân tối: \(\left\{ \begin{array}{l}{x_s} = k.i\\{x_t} = \left( {k + \frac{1}{2}} \right)i\end{array} \right.;\,\,k \in Z\)

Nếu: \(\frac{x}{i} = k;\,k \in Z\) → Vân sáng bậc k

Nếu: \(\frac{x}{i} = k + \frac{1}{2};\,k \in Z\) → Vân tối thứ (k + 1)

Cách giải:

Công thức khoảng vân \(i = \frac{{\lambda D}}{a} = \frac{{0,64.1}}{{0,4}} = 1,6mm\)

Ta có: \(\frac{x}{i} = \frac{{5,6}}{{1,6}} = 3,5 = 3 + \frac{1}{2} \Rightarrow k = 3\)

→ Tại M là vân tối thứ 4.

Chọn C.

Câu 20:

Phương pháp:

Khoảng vân: \(i = \frac{{\lambda D}}{a}\)

Vì ba ánh sáng cùng cho các vân sáng, nên vị trí ba vân sáng trùng nhau thỏa mãn :\(x = {k_1}.\frac{{{\lambda _1}.D}}{a} = {k_2}.\frac{{{\lambda _2}.D}}{a} = {k_3}.\frac{{{\lambda _3}.D}}{a} \Rightarrow {i_1}:{i_2}:{i_3} = {\lambda _1}:{\lambda _2}:{\lambda _3} = a:b:c\)

Khi xác định vị trí vân sáng của một ánh sáng đơn sắc, ta tìm số vân trong khoảng giữa hai vân sáng trùng 3 màu trừ đi số vân sáng trùng hai màu từng cặp.

Cách giải:

Áp dụng công thức tính khoảng vân \(i = \frac{{\lambda D}}{a}\)

Vì ba ánh sáng cùng cho các vân sáng, nên vị trí ba vân sáng trùng nhau thỏa mãn :\(\begin{array}{l}x = {k_1}.\frac{{{\lambda _1}.D}}{a} = {k_2}.\frac{{{\lambda _2}.D}}{a} = {k_3}.\frac{{{\lambda _3}.D}}{a}\\ \Rightarrow {i_1}:{i_2}:{i_3} = {\lambda _1}:{\lambda _2}:{\lambda _3} = a:b:c = 0,4:0,5:0,6 = 4:5:6\end{array}\)

Ta xét vân trung tâm và vân trùng 3 màu đầu tiên, ứng với vị trí:

\[x = 15{i_1} = 12{i_2} = 10{i_3}\]

Vị trí trùng nhau của hai bước sóng λ₁ và λ₂ có khoảng vân trùng cặp 12 là:

\[{i_{12}} = 5{i_1} = 4{i_2}\]

Vậy trong khoảng từ vân trung tâm đến vân trùng 3 màu đầu tiên có số vị trí trùng nhau của hai bước sóng λ₁ và λ₂ là:

 (15:5)-1=2

Vị trí trùng nhau của hai bước sóng λ₁ và λ₃ có khoảng vân trùng cặp 13 là:

 \({i_{13}} = 3{i_1} = 2{i_3}\) 

Vậy trong khoảng từ vân trung tâm đến vân trùng 3 màu đầu tiên có số vị trí trùng nhau của hai bước sóng λ₁ và λ₃ là:

 (15:3)-1=4

Vị trí trùng nhau của hai bước sóng λ₂ và λ₃ có khoảng vân trùng cặp 23 là:

\[{i_{23}} = 6{i_2} = 5{i_3}\]

Vậy trong khoảng từ vân trung tâm đến vân trùng 3 màu đầu tiên có số vị trí trùng nhau của hai bước sóng λ₂ và λ₃là:

 (12:6)-1=1 

Vậy số vị trí chỉ có 1 vạch màu đơn sắc là :

\((15 + 12 + 10) - (1.3 + 2.2 + 2.4 + 2.1) = 20\)

Chọn B.

Câu 21:

Phương pháp:

Năng lượng của photon : \(\varepsilon  = \dfrac{{hc}}{\lambda } = hf\)

Công suất phát: \(P = N.\varepsilon \)

Cách giải:

Công suất phát: \(P = N.\varepsilon  = N.hf\)

Suy ra: \(N = \dfrac{P}{{hf}} = \dfrac{{0,4}}{{6,{{625.10}^{ - 34}}.7,{{5.10}^{14}}}}\)

\(= 8,{05.10^{17}}\) 

Chọn C.

Câu 22:

Phương pháp:

Lực tương tác giữa êlectron và hạt nhân của nguyên tử Hidro trên các quỹ đạo là \(F = k.\frac{{|{q_e}.{q_p}|}}{{r_n^2}}\)

Bán kính quỹ đạo dừng thứ n: \({r_n} = {n^2}.{r_0}\)

Cách giải:

Sử dụng bảng mức năng lượng và tên các quỹ đạo.

 

Lực tương tác giữa êlectron và hạt nhân của nguyên tử Hidro trên quỹ đạo K là :

 \(F = k.\frac{{|{q_e}.{q_p}|}}{{{r_0}^2}}\)

Lực tương tác giữa êlectron và hạt nhân của nguyên tử Hidro trên quỹ đạo M là :

\({F_M} = k.\frac{{|{q_e}.{q_p}|}}{{{{\left( {{3^2}{r_0}} \right)}^2}}} = k.\frac{{|{q_e}.{q_p}|}}{{81{r_0}^2}} = \frac{F}{{81}}\)

Chọn C.

Câu 23:

Phương pháp:

Số hạt nhân mẹ còn lại sau thời gian t được xác định bởi: \(N = {N_0}{.2^{\frac{{ - t}}{T}}}\)

Số hạt nhân con được tạo thành hay số hạt nhân mẹ đã bị phân rã sau thời gian t được xác định bởi:

\(N' = {N_0} - N = {N_0}.(1 - {2^{\frac{{ - t}}{T}}})\)

Cách giải:

Số hạt nhân mẹ còn lại sau thời gian t được xác định bởi: \(N = {N_0}{.2^{\frac{{ - t}}{T}}}\)

Số hạt nhân con được tạo thành hay số hạt nhân mẹ đã bị phân rã sau thời gian t được xác định bởi:

\(\begin{array}{l}N' = {N_0} - N = {N_0}.(1 - {2^{\frac{{ - t}}{T}}}) = 70\% {N_0}\\ \Rightarrow (1 - {2^{\frac{{ - t}}{T}}}) = 70\%  = 0,7 \Rightarrow {2^{\frac{{ - t}}{T}}} = 0,3\\ \Rightarrow t =  - T.{\log _2}(0,3) = 1,74T = 1,74.3,8 = 6,6\end{array}\)

Vậy thời gian là 6,6 ngày.

Chọn A.

Câu 24:

Phương pháp:

Áp dụng công thức tính độ hụt khối: \(\Delta m = \left[ {Z.{m_p} + \left( {A - Z} \right).{m_n}} \right] - {m_X}\)

Cách giải:

Độ hụt khối của hạt nhân \({}_4^{10}Be\) là:

\(\begin{array}{l}\Delta m = \left[ {Z.{m_p} + \left( {A - Z} \right).{m_n}} \right] - {m_X}\\ \Rightarrow \Delta m = \left[ {4.1,0073 + (10 - 4).1,0087} \right] - 10,0113 = 0,0701u\end{array}\)

Chọn B. 

Nguồn: Sưu tầm

Loigiaihay.com