Đề kiểm tra giữa kì II Toán 6 - Đề số 5 có lời giải chi tiếtĐề kiểm tra giữa kì 2 toán 6 - Đề số 5 có lời giải chi tiết Quảng cáo
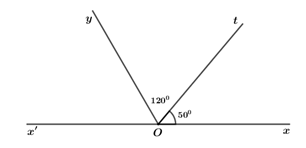
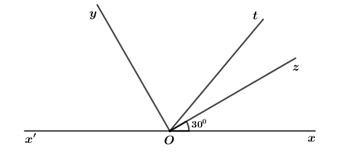
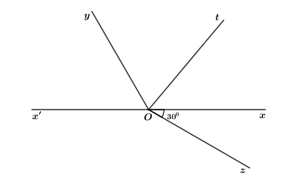
Đề bài Câu 1 (2,5 điểm): 1. Thực hiện phép tính: \(A = {\left( { - 3} \right)^2} + 5.{\left( { - 2} \right)^3} + 58:\left( { - 2} \right)\) 2. Tìm rồi tính tổng tất các ước nguyên nhỏ hơn \(6\) của \( - 12\). 3. So sánh hai phân số sau: \(\frac{{ - 7}}{{72}};\,\,\frac{9}{{ - 40}}\) Câu 2 (2 điểm): 1. Tìm số nguyên \(x\), biết \(218 - \left( {x + 31} \right) = x - 29\) 2. Tìm các số nguyên \(x\) sao cho \(\frac{{ - 5}}{2} < \frac{3}{x} < \frac{2}{{ - 3}}\) Câu 3 (2 điểm): Trên cùng một thửa ruộng, ba máy cày nếu cày riêng một mình thì thời gian cày xong thửa ruộng đó lần lượt là \(2\) ngày, \(3\) ngày và \(7\) ngày. Nếu cả ba máy cày cùng cày chung trên thửa ruộng đó thì trong một ngày cày được bao nhiêu phần thửa ruộng và trong một ngày có cày xong thửa ruộng đó không? Câu 4 (3 điểm): Cho hai tia \(Oy\) và \(Ot\) cùng nằm trên một nửa mặt phẳng có bờ chứa tia \(Ox\). Biết \(\angle xOt = {50^0}\) và \(\angle xOy = {120^0}\). 1. Trong \(3\) tia \(Ox,\,\,Oy,\,\,Ot\) tia nào nằm giữa hai tia còn lại? Vì sao? Tính số đo \(\angle yOt\)? 2. Kẻ tia \(Ox'\) là tia đối của tia \(Ox\). Tính số đo \(\angle x'Ot\)? 3. Vẽ tia \(Oz\) sao cho \(\angle xOz = {30^0}\). Tính số đo \(\angle zOy\)? Câu 5 (0,5 điểm): Tìm các số nguyên dương \(x,\,\,y\) biết rằng \(\frac{1}{x} + \frac{y}{2} = \frac{5}{8}\). Lời giải chi tiết Câu 1 (TH) Phương pháp: 1. Áp dụng các công thức lũy thừa, phép toán với số nguyên để thực hiện phép tính 2. Xác định các ước của \( - 12\), từ đó tìm các ước nhỏ hơn \(6\) và tính tổng. 3. Xác định MSC, quy đồng mẫu số hai phân số và so sánh tử số. Cách giải: 1. Thực hiện phép tính: \(A = {\left( { - 3} \right)^2} + 5.{\left( { - 2} \right)^3} + 58:\left( { - 2} \right)\) \(\begin{array}{l}A = {\left( { - 3} \right)^2} + 5.{\left( { - 2} \right)^3} + 58:\left( { - 2} \right)\\\,\,\,\,\, = 9 + 5.\left( { - 8} \right) + \left( { - 29} \right)\\\,\,\,\,\, = 9 + \left( { - 40} \right) + \left( { - 29} \right)\\\,\,\,\,\, = \left[ {9 + \left( { - 29} \right)} \right] + \left( { - 40} \right)\\\,\,\,\,\, = \left( { - 20} \right) + \left( { - 40} \right)\\\,\,\,\,\, = - 60\end{array}\) 2. Tìm rồi tính tổng tất các ước nguyên nhỏ hơn \(6\) của \( - 12\). Ta có: Ư\(\left( { - 12} \right) = \left\{ { - 12;\,\, - 6;\,\, - 4;\,\, - 3;\,\, - 2;\,\, - 1;\,\,1;\,\,2;\,\,3;\,\,4;\,\,6;\,\,12} \right\}\) Tổng tất cả ước nguyên nhỏ hơn \(6\) của \( - 12\) là: \(\begin{array}{l}\left( { - 12} \right) + \,\left( { - 6} \right) + \left( { - 4} \right) + \,\left( { - 3} \right) + \left( { - 2} \right) + \left( { - 1} \right) + \,\,1 + \,2 + 3 + \,4\\ = \left( { - 12} \right) + \,\left( { - 6} \right) + \left[ {\left( { - 4} \right) + \,4} \right] + \left[ {\left( { - 3} \right) + 3} \right] + \left[ {\left( { - 2} \right) + 2} \right] + \left[ {\left( { - 1} \right) + 1} \right]\\ = \left( { - 12} \right) + \,\left( { - 6} \right) + 0 + 0 + 0 + 0\\ = - 18\end{array}\) 3. So sánh hai phân số sau \(\frac{{ - 7}}{{72}};\,\,\frac{9}{{ - 40}}\) Ta có : \(72 = {2^3}{.3^2};\)\(40 = {2^3}.5\) \( \Rightarrow {\mathop{\rm MSC}\nolimits} \left( {72,\,\,40} \right) = {2^3}{.3^2}.5\)\( = 360\) \(\frac{{ - 7}}{{72}} = \frac{{ - 7.5}}{{72.5}} = \frac{{ - 35}}{{360}}\) \(\frac{9}{{ - 40}} = \frac{{ - 9}}{{40}} = \frac{{ - 9.9}}{{40.9}} = \frac{{ - 81}}{{360}}\) Vì \( - 35 > - 81\) nên \(\frac{{ - 35}}{{360}} > \frac{{ - 81}}{{360}}\). Vậy \(\frac{{ - 7}}{{72}} > \frac{9}{{ - 40}}\). Câu 2 (VD) Phương pháp: 1. Giải bài toán ngược để tìm \(x\) 2. Quy đồng tử số và áp dụng quy tắc so sánh các phân số cùng tử. Cách giải: 1. Tìm số nguyên \(x\), biết \(218 - \left( {x + 31} \right) = x - 29\) \(\begin{array}{l}218 - \left( {x + 31} \right) = x - 29\\218 - x - 31 = x - 29\\ - x - x = - 29 - 218 + 31\\ - 2x = - 247 + 31\\ - 2x = - 216\\x = \left( { - 216} \right):\left( { - 2} \right)\\x = 108\end{array}\) Vậy \(x = 108\). 2. Tìm các số nguyên \(x\) sao cho \(\frac{{ - 5}}{2} < \frac{3}{x} < \frac{2}{{ - 3}}\) \(\frac{{ - 5}}{2} < \frac{3}{x} < \frac{2}{{ - 3}}\) Điều kiện: \(x \ne 0\) \(\begin{array}{l} \Rightarrow \frac{{30}}{{ - 12}} < \frac{{30}}{{10x}} < \frac{{30}}{{ - 45}}\\ \Rightarrow - 45 < 10x < - 12\\ \Rightarrow \frac{{ - 45}}{{10}} < x < \frac{{ - 12}}{{10}}\\ \Rightarrow - 4,5 < x < - 1,2\end{array}\) Mà \(x \in \mathbb{Z}\) nên \(x \in \left\{ { - 4;\,\, - 3;\,\, - 2} \right\}\). Vậy \(x \in \left\{ { - 4;\,\, - 3;\,\, - 2} \right\}\). Câu 3 (VD) Phương pháp: Xác định lượng công việc mà mỗi máy cày cày được trong \(1\) ngày nếu cày riêng một mình. Tính lượng công việc mà cả ba máy cày chung, từ đó suy ra thời gian để cả ba máy cày xong thừa ruộng sau đó so sánh với \(1\). Cách giải: Trong một ngày, nếu cày riêng một mình máy thứ nhất cày được \(\frac{1}{2}\) thửa ruộng; máy thứ hai cày được \(\frac{1}{3}\) thửa ruộng; máy thứ ba cày được \(\frac{1}{7}\) thửa ruộng. Trong một ngày, nếu cả ba máy cày cùng cày chung thì cày được là : \(\frac{1}{2} + \frac{1}{3} + \frac{1}{7} = \frac{{41}}{{42}}\) thửa ruộng. Ba máy cày nếu cày chung thì thời gian cày xong thửa ruộng đó là : \(\frac{1}{{\frac{{41}}{{42}}}} = \frac{{42}}{{41}}\) ngày. Vì \(42 > 41\) nên \(\frac{{42}}{{41}} > 1\). Do đó, trong một ngày nếu cày chung thì cả ba máy có cày xong thửa ruộng. Câu 4 (VD) Phương pháp: 1. Áp dụng dấu nhận biết tia nằm giữa hai tia. 2. \(Ox\) và \(Ox'\) là hai tia đối nhau nên \(\angle xOx' = {180^0}\). 3. Xét hai trường hợp: + Hai tia \(Oy,\,\,Oz\) nằm trên cùng một nửa mặt phẳng có bờ chứa tia \(Ox\); + Hai tia \(Oy,\,\,Oz\) nằm trên hai nửa mặt phẳng đối nhau có bờ chứa tia \(Ox\) Cách giải: 1. Trong \(3\) tia \(Ox,\,\,Oy,\,\,Oz\) tia nào nằm giữa hai tia còn lại? Vì sao? Tính số đo \(\angle yOt\)? Trên nửa mặt phẳng có bờ chứa tia \(Ox\), có \(\angle xOt < \angle xOy\,\,\left( {v\`i \,\,{{50}^0} < {{120}^0}} \right)\). Do đó, tia \(Ot\) nằm giữa hai tia \(Ox\) và \(Oy\). Vì tia \(Ot\) nằm giữa hai tia \(Ox\) và \(Oy\)nên ta có: \(\angle xOt + \angle yOt = \angle xOy\) (tính chất) \(\begin{array}{l} \Rightarrow \angle yOt = \angle xOy - \angle xOt\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {120^0} - {50^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {70^0}\end{array}\) Vậy \(\angle yOt = {70^0}\). 2. Kẻ tia \(Ox'\) là tia đối của tia \(Ox\). Tính số đo \(\angle x'Ot\). Vì \(Ox\) và \(Ox'\) là hai tia đối nhau nên \(\angle xOt\) và \(\angle x'Ot\) là hai góc kề bù. Khi đó, ta có: \(\angle xOt + \angle x'Ot = {180^0}\) (tính chất) \(\begin{array}{l} \Rightarrow \angle x'Ot = {180^0} - \angle xOt\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {180^0} - {50^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {130^0}\end{array}\) Vậy \(\angle x'Ot = {130^0}\). 3. Vẽ tia \(Oz\) sao cho \(\angle xOz = {30^0}\). Tính số đo \(\angle zOy\). Trường hợp 1: Hai tia \(Oy,\,\,Oz\) nằm trên cùng một nửa mặt phẳng có bờ chứa tia \(Ox\) Trên cùng một nửa mặt phẳng có bờ chứa tia \(Ox\), ta có \(\angle xOz < \angle xOy\) (vì \({30^0} < {120^0}\)) suy ra tia \(Oz\) nằm giữa hai tia \(Ox\) và \(Oy\). Vì tia \(Oz\) nằm giữa hai tia \(Ox\) và \(Oy\) nên ta có: \(\angle xOz + \angle zOy = \angle xOy\) (tính chất) \(\begin{array}{l} \Rightarrow \angle zOy = \angle xOy - \angle xOz\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {120^0} - {30^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {90^0}\end{array}\) Trường hợp 2: Hai tia \(Oy,\,\,Oz\) nằm trên hai nửa mặt phẳng đối nhau có bờ chứa tia \(Ox\) Vì\(\,Oy,\,\,Oz\)nằm trên hai nửa mặt phẳng đối nhau có bờ chứa tia \(Ox\) và \(\angle zOx + \angle xOy = {30^0} + {120^0}\)\( = {150^0} < {180^0}\) \( \Rightarrow \) Tia \(Ox\) nằm giữa hai tia \(Oy\) và \(Oz\) \( \Rightarrow \angle zOx + \angle xOy = \angle yOz\) (tính chất) \(\begin{array}{l} \Rightarrow \angle yOz = {30^0} + {120^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {150^0}\end{array}\) Vậy \(\angle yOz = {90^0}\) hoặc \(\angle yOz = {150^0}\). Câu 5 (VDC) Phương pháp: Xét \(\frac{1}{x} \le 1,\,\,\frac{5}{8} < 1\)\( \Rightarrow \frac{1}{x} + \frac{5}{8} \le 1 \Rightarrow \frac{y}{2} < 1\). Từ đó, chọn được giá trị của \(y\) và tìm được \(x\). Cách giải: Vì \(x\) là số nguyên dương nên \(x \ge 1 \Rightarrow \frac{1}{x} \le 1\). Vì \(\frac{5}{8} < 1\,\left( {5 < 8} \right)\) nên \(\frac{1}{x} + \frac{y}{2} < 1\). Vì \(\frac{1}{x} \le 1\) nên để \(\frac{1}{x} + \frac{y}{2} < 1\) thì \(\frac{y}{2} < 1 \Rightarrow y < 2\). Mà \(y\) là số nguyên dương nên \(y = 1\). Với \(y = 1\) ta có: \(\begin{array}{l}\,\,\,\,\,\,\frac{1}{x} + \frac{1}{2} = \frac{5}{8}\\ \Rightarrow \frac{1}{x} = \frac{1}{8}\\ \Rightarrow x = 8\,\left( {tm} \right)\end{array}\) Vậy \(x = 8;\,\,y = 1\).
|




















Danh sách bình luận