Đề kiểm tra giữa kì II Toán 6 - Đề số 1 có lời giải chi tiết

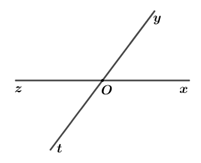
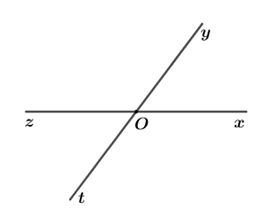
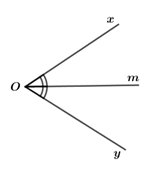
Đề bài

Phần I: Trắc nghiệm (2,0 điểm)

Viết vào bài thi chữ cái in hoa đứng trước câu trả lời mà em chọn:

Câu 1. Số đối của số \(\frac{3}{5}\) là

A. \(\frac{3}{{ - 5}}\)                                            B. \(\frac{5}{3}\)

C. \(\frac{{ - 5}}{3}\)                                              D. \(\frac{2}{5}\)

Câu 2. Kết quả của phép tính \( - 1 + \frac{2}{3}\) là

A. \(\frac{5}{3}\)                                      B. \(\frac{{ - 5}}{3}\)    

C. \(\frac{{ - 1}}{3}\)                                          D. \(\frac{1}{3}\)

Câu 3. Số cặp góc kề bù có trong hình vẽ bên là:

A. \(1\)                                                 B. \(2\)

C. \(3\)                                            D. \(4\)

Câu 4. Tia \(Om\) là tia phân giác của góc \(xOy\) khi

A. \(\angle xOm = \angle xOy:2\)                                                

B. Tia \(Om\) nằm giữa hai tia \(Ox,\,\,Oy\)                                  

C. \(\angle xOm = \angle mOy\) và tia \(Om\) nằm giữa hai tia \(Ox,\,\,Oy\)      

D. \(\angle xOm = \angle mOy = \angle xOy:2\)

Phần II: Tự luận (8,0 điểm)

Câu 1: Thực hiện phép tính

a) \({27.5^2} - 25.127\)                                                                  

b) \(\frac{{ - 5}}{{12}} + \frac{3}{4} + \frac{1}{{ - 3}}\)

c) \(\frac{5}{9} \cdot \frac{7}{{13}} + \frac{5}{9} \cdot \frac{9}{{13}} + \frac{3}{{13}} \cdot \frac{{ - 5}}{9}\)

d) \(3,2.\frac{{15}}{{64}} - \left( {\frac{4}{5} + \frac{2}{3}} \right):\frac{{11}}{3}\)

Câu 2: Tìm \(x\) biết:

a) \( - 3x + 10 = 1\)

b) \(\frac{7}{8} + x = \frac{3}{5}\)

c) \(\frac{1}{3}:\left( {2x - 1} \right) = \frac{{ - 4}}{{21}}\)

d) \(\frac{{17}}{2} - \left| {x - \frac{3}{4}} \right| = \frac{{ - 7}}{4}\)

Câu 3: Trên cùng một nửa mặt phẳng bờ chứa tia \(Ox\) vẽ \(\angle xOy = {70^0},\)\(\angle xOz = {140^0}\).

a) Trong ba tia \(Ox,\,\,Oy,\,\,Oz\) tia nào nằm giữa hai tia còn lại? Vì sao?

b) Tính số đo của \(\angle yOz\).

c) Tia \(Oy\) có là tia phân giác của \(\angle xOz\) không? Vì sao?

d) Vẽ tia \(Om\) là tia đối của tia \(Ox\). Tính số đo của \(\angle mOz\).

Câu 4: Tính giá trị của biểu thức sau:

\(M = \frac{{{3^2}}}{{2.5}} + \frac{{{3^2}}}{{5.8}} + \frac{{{3^2}}}{{8.11}} +  \ldots  + \frac{{{3^2}}}{{98.101}}\)

Lời giải chi tiết

Phần I: Trắc nghiệm  

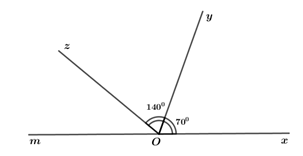
Câu 1 (TH) - Số đối

Phương pháp:

Hai số gọi là đối nhau nếu tổng của chúng bằng \(0\).

Cách giải:

Số đối của \(\frac{3}{5}\) là \(\frac{{ - 3}}{5} =  - \frac{3}{5} = \frac{3}{{ - 5}}\).

Chọn A.

Câu 2 (TH) - Phép cộng phân số

Phương pháp:

Áp dụng quy tắc cộng hai phân số không cùng mẫu.

Cách giải:

Ta có: \( - 1 + \frac{2}{3}\)\( = \frac{{ - 3}}{3} + \frac{2}{3}\)\( = \frac{{ - 3 + 2}}{3}\)\( = \frac{{ - 1}}{3}\)

Chọn C.

Câu 3 (TH) - Khi nào thì góc xOy + góc yOz = góc xOz?

Phương pháp:

Áp dụng lý thuyết: Hai góc vừa kề nhau, vừa bù nhau là hai góc kề bù. Hai góc kề bù có tổng số đo là \({180^0}\).

Cách giải:

Các cặp góc kề bù trong hình vẽ trên là: \(\angle xOy\) và \(\angle yOz\); \(\angle xOy\) và \(\angle xOt\); \(\angle xOt\) và \(\angle zOt\); \(\angle zOt\) và \(\angle yOz\)

Vậy có \(4\) cặp góc kề bù trong trong hình vẽ trên.

Chọn D.

Câu 4 (NB) - Tia phân giác của góc

Phương pháp:

Áp dụng định nghĩa tia phân giác: Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.

Cách giải:

Theo định nghĩa, \(Om\)là tia phân giác của góc \(\angle xOy\) nếu thỏa mãn điều kiện sau:

+ Tia \(Om\) nằm giữa hai tia \(Ox\) và \(Oy\)

+ \(\angle xOm = \angle mOy\)

Chọn C.

II. TỰ LUẬN

Câu 1 (VD) - Nhân hai số nguyên khác dấu; Phép cộng, trừ, nhân, chia  phân số

Phương pháp:

a) Áp dụng phương pháp đặt nhân tử chung.

b) Thực hiện theo thứ tự thực hiện phép tính, quy tắc cộng các phân số.

c) Áp dụng phương pháp đặt nhân tử chung.

d) Thực hiện theo thứ tự thực hiện phép tính, các quy tắc tính toán với phân số.    

Cách giải:

Thực hiện phép tính:

a) \({27.5^2} - 25.127\)

\(\begin{array}{l}\,\,\,\,{27.5^2} - 25.127\\ = 27.25 - 25.127\\ = \left( {27 - 127} \right).25\\ =  - 100.25\\ =  - 2500\end{array}\)

b) \(\frac{{ - 5}}{{12}} + \frac{3}{4} + \frac{1}{{ - 3}}\)

\(\begin{array}{l}\,\,\,\,\frac{{ - 5}}{{12}} + \frac{3}{4} + \frac{1}{{ - 3}}\\ = \frac{{ - 5}}{{12}} + \frac{9}{{12}} - \frac{4}{{12}}\\ = \frac{{ - 5 + 9 - 4}}{{12}} = 0\end{array}\)

c) \(\frac{5}{9} \cdot \frac{7}{{13}} + \frac{5}{9} \cdot \frac{9}{{13}} + \frac{3}{{13}} \cdot \frac{{ - 5}}{9}\)

\(\begin{array}{l}\,\,\,\,\frac{5}{9} \cdot \frac{7}{{13}} + \frac{5}{9} \cdot \frac{9}{{13}} + \frac{3}{{13}} \cdot \frac{{ - 5}}{9}\\ = \frac{5}{9} \cdot \frac{7}{{13}} + \frac{5}{9} \cdot \frac{9}{{13}} - \frac{3}{{13}} \cdot \frac{5}{9}\\ = \frac{5}{9} \cdot \left( {\frac{7}{{13}} + \frac{9}{{13}} - \frac{3}{{13}}} \right)\\ = \frac{5}{9} \cdot \left( {\frac{{16}}{{13}} - \frac{3}{{13}}} \right)\\ = \frac{5}{9} \cdot \frac{{13}}{{13}}\\ = \frac{5}{9}\end{array}\)

d) \(3,2.\frac{{15}}{{64}} - \left( {\frac{4}{5} + \frac{2}{3}} \right):\frac{{11}}{3}\)

\(\begin{array}{l}\,\,\,\,3,2.\frac{{15}}{{64}} - \left( {\frac{4}{5} + \frac{2}{3}} \right):\frac{{11}}{3}\\ = \frac{{16}}{5}.\frac{{15}}{{64}} - \left( {\frac{{12}}{{15}} + \frac{{10}}{{15}}} \right):\frac{{11}}{3}\\ = \frac{{16}}{5}.\frac{{15}}{{64}} - \frac{{22}}{{15}}:\frac{{11}}{3}\\ = \frac{{16}}{5}.\frac{{15}}{{64}} - \frac{{22}}{{15}} \cdot \frac{3}{{11}}\\ = \frac{3}{4} - \frac{2}{5}\\ = \frac{{15}}{{20}} - \frac{8}{{20}}\\ = \frac{7}{{20}}\end{array}\)

Câu 2 (VD): - Ôn tập chương 3: Phân số

Phương pháp:

Giải bài toán ngược để tìm \(x\).

Cách giải:

Tìm \(x\) biết:

a) \( - 3x + 10 = 1\)

\(\begin{array}{l} - 3x + 10 = 1\\\,\,\,\,\,\,\,\,\, - 3x =  - 9\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \left( { - 9} \right):\left( { - 3} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 3\end{array}\)

Vậy \(x = 3\).

b) \(\frac{7}{8} + x = \frac{3}{5}\)

\(\begin{array}{l}\frac{7}{8} + x = \frac{3}{5}\\\,\,\,\,\,\,\,\,x = \frac{3}{5} - \frac{7}{8}\\\,\,\,\,\,\,\,\,x = \frac{{24}}{{40}} - \frac{{35}}{{40}}\\\,\,\,\,\,\,\,\,x = \frac{{ - 11}}{{40}}\end{array}\)

Vậy \(x = \frac{{ - 11}}{{40}}\).

c) \(\frac{1}{3}:\left( {2x - 1} \right) = \frac{{ - 4}}{{21}}\)

\(\begin{array}{l}\frac{1}{3}:\left( {2x - 1} \right) = \frac{{ - 4}}{{21}}\\\,\,\,\,\,\,\,\,\,\,2x - 1 = \frac{1}{3}:\left( {\frac{{ - 4}}{{21}}} \right)\\\,\,\,\,\,\,\,\,\,\,2x - 1 = \frac{{ - 7}}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2x = \frac{{ - 7}}{4} + 1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2x = \frac{{ - 3}}{4}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \frac{{ - 3}}{4}:2\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \frac{{ - 3}}{4} \cdot \frac{1}{2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \frac{{ - 3}}{8}\end{array}\)

Vậy \(x = \frac{{ - 3}}{8}\).

d) \(\frac{{17}}{2} - \left| {x - \frac{3}{4}} \right| = \frac{{ - 7}}{4}\)

\(\begin{array}{l}\frac{{17}}{2} - \left| {x - \frac{3}{4}} \right| = \frac{{ - 7}}{4}\\\left| {x - \frac{3}{4}} \right| = \frac{{17}}{2} - \left( {\frac{{ - 7}}{4}} \right)\\\left| {x - \frac{3}{4}} \right| = \frac{{17}}{2} + \frac{7}{4}\\\left| {x - \frac{3}{4}} \right| = \frac{{34}}{4} + \frac{7}{4}\\\left| {x - \frac{3}{4}} \right| = \frac{{41}}{4}\end{array}\)

Trường hợp 1:

\(\begin{array}{l}x - \frac{3}{4} = \frac{{41}}{4}\\x = \frac{{41}}{4} + \frac{3}{4}\\x = \frac{{44}}{4}\\x = 11\end{array}\)

Trường hợp 2:

\(\begin{array}{l}x - \frac{3}{4} =  - \frac{{41}}{4}\\x =  - \frac{{41}}{4} + \frac{3}{4}\\x =  - \frac{{38}}{4}\\x =  - \frac{{19}}{2}\end{array}\)

Vậy \(x \in \left\{ { - \frac{{19}}{2};\,\,11} \right\}\).

Câu 3 (VD) - Ôn tập chương 2: Góc

Phương pháp:

a) Áp dụng dấu hiệu nhận biết tia nằm giữa hai tia.

b) Nếu tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) thì\(\angle xOy + \angle yOz = \angle xOz\).

c) \(Om\) là tia phân giác của \(\angle xOy\) nếu thỏa mãn điều kiện sau:

+ Tia \(Om\) nằm giữa hai tia \(Ox\) và \(Oy\)

+ \(\angle xOm = \angle mOy\)

d) Áp dụng lý thuyết về hai tia đối nhau, hai góc kề bù.

Cách giải:

Trên cùng một nửa mặt phẳng bờ chứa tia \(Ox\) vẽ \(\angle xOy = {70^0},\)\(\angle xOz = {140^0}\).

a) Trong ba tia \(Ox,\,\,Oy,\,\,Oz\) tia nào nằm giữa hai tia còn lại? Vì sao?

Trên cùng một nửa mặt phẳng có bờ chứa tia \(Ox\), có \(\angle xOy < \angle xOz\)\(\left( {{{70}^0} < {{140}^0}} \right)\) suy ra tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\).

b) Tính số đo góc \(yOz\).

Vì tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) nên ta có:

\(\begin{array}{l}\angle xOy + \angle yOz = \angle xOz\\ \Leftrightarrow \angle yOz = \angle xOz - \angle xOy\\ \Leftrightarrow \angle yOz = {140^0} - {70^0}\\ \Leftrightarrow \angle yOz\, = {70^0}\end{array}\)

Vậy \(\angle yOz = {70^0}\).

c) Tia \(Oy\) có là tia phân giác của \(\angle xOz\) không? Vì sao?

Ta có:

+ Tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) (câu a)

+ \(\angle xOy = \angle yOz = {70^0}\)(câu b)

Suy ra, tia \(Oy\) là tia phân giác của \(\angle xOz\) (định nghĩa)

d) Vẽ tia \(Om\) là tia đối của tia \(Ox\). Tính số đo của \(\angle mOz\).

Vì \(Ox\) và \(Om\) là hai tia đối nhau nên \(\angle xOm = {180^0}\).

Suy ra, \(\angle xOz\) và \(\angle xOm\) là hai góc kề bù.

 Khi đó, ta có:

\(\begin{array}{l}\angle xOz + \angle zOm = {180^0}\\ \Leftrightarrow \angle zOm = {180^0} - \angle xOz\\ \Leftrightarrow \angle zOm = {180^0} - {140^0}\\ \Leftrightarrow \angle zOm = {40^0}\end{array}\)

Vậy \(\angle zOm = {40^0}\).

Câu 4 (VDC) - Ôn tập chương 3: Phân số

Phương pháp:

Áp dụng:

\(\frac{{n - k}}{{n.k}} = \frac{n}{{n.k}} - \frac{k}{{n.k}}\)\( = \frac{1}{k} - \frac{1}{n}\,\,\)\(\left( {k,n \in \mathbb{N};\,\,k < n} \right)\)

Cách giải:

Tính giá trị của biểu thức sau:

 \(M = \frac{{{3^2}}}{{2.5}} + \frac{{{3^2}}}{{5.8}} + \frac{{{3^2}}}{{8.11}} +  \ldots  + \frac{{{3^2}}}{{98.101}}\)

\(\begin{array}{l}M = \frac{{{3^2}}}{{2.5}} + \frac{{{3^2}}}{{5.8}} + \frac{{{3^2}}}{{8.11}} +  \ldots  + \frac{{{3^2}}}{{98.101}}\\\,\,\,\,\,\,\, = 3.\left( {\frac{3}{{2.5}} + \frac{3}{{5.8}} + \frac{3}{{8.11}} +  \ldots  + \frac{3}{{98.101}}} \right)\\\,\,\,\,\,\,\, = 3.\left( {\frac{1}{2} - \frac{1}{5} + \frac{1}{5} - \frac{1}{8} + \frac{1}{8} - \frac{1}{{11}} +  \ldots  + \frac{1}{{98}} - \frac{1}{{101}}} \right)\\\,\,\,\,\,\,\, = 3.\left( {\frac{1}{2} - \frac{1}{{101}}} \right)\\\,\,\,\,\,\,\, = 3 \cdot \frac{{99}}{{202}}\\\,\,\,\,\,\,\, = \frac{{297}}{{202}}\end{array}\)

Vậy \(M = \frac{{297}}{{202}}\).