Đề kiểm tra 45 phút (1 tiết) - Đề số 6 - Chương 3 - Hình học 7

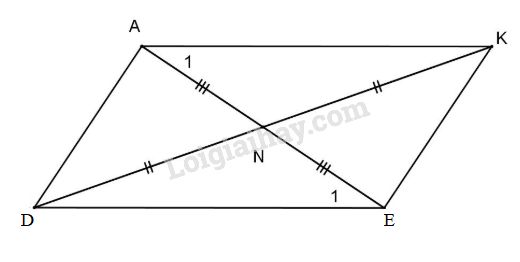
Đề bài

Bài 1: Cho tam giác ABC có \(\widehat A = {55^0},\widehat B = {65^0}.\) Hãy so sánh các cạnh của tam giác ABC.

Bài 2: Cho tam giác ADE vuông tại A có AD = 8cm, AE = 15 cm.

a) Tính độ dài đoạn DE.

b) Gọi N là trung điểm của AE. Trên tia đối của tia ND lấy điểm K sao cho \(N{\rm{D}} = NK.\) Chứng minh: \(\Delta AN{\rm{D}} = \Delta ENK\); so sánh độ dài đoạn thẳng AD và EK.

e) Chứng minh AK và DE song song với nhau.

d) Chứng minh: \(A{\rm{D}} + DE > 2{\rm{D}}N.\) 

LG bài 1

Phương pháp giải:

+Tổng ba góc trong 1 tam giác bằng 180 độ

+ Trong 1 tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn

Lời giải chi tiết:

Ta có \(\widehat A + \widehat B + \widehat C = {180^0}\) (tổng ba góc trong tam giác)

\(\eqalign{  &  \Rightarrow \widehat C = {180^0} - (\widehat B + \widehat A) \cr&\Rightarrow \widehat C = {180^0} - ({65^0} + {55^0})  \cr   &  \Rightarrow \widehat C = {180^0} - {120^0} = {60^0}. \cr} \)

Do đó \(\widehat B > \widehat C > \widehat A\) (\({65^0} > {60^0} > {55^0}\))

\( \Rightarrow AC > AB > BC.\)

(quan hệ cạnh và góc đối diện)

LG bài 2

Phương pháp giải:

+Định lý Py-ta-go

+Nếu 1 đường thẳng cắt hai đường thẳng, các cặp góc tạo thành có 1 cặp góc so le trong bằng nhau thì hai đường thẳng đó song song

 +Trong một tam giác độ dài 1 cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại

Lời giải chi tiết:

a) \(\Delta A{\rm{D}}E\) vuông tại A

Ta có \(D{E^2} = D{A^2} + E{{\rm{A}}^2}\) (định lý Pytago)

\(\eqalign{ &  \Leftrightarrow D{E^2} = {8^2} + {15^2}  \cr  &  \Leftrightarrow D{E^2} = 289  \cr   &  \Rightarrow DE = 17cm. \cr} \)

b) Xét \(\Delta AN{\rm{D}}\) và \(\Delta ENK.\)

Có \(AN = A{\rm{E}}\) (gt);

\(DN = KN\) (gt)

\(\widehat {AN{\rm{D}}} = \widehat {ENK}\) (đối đỉnh).

Do đó \(\Delta AN{\rm{D}} = \Delta ENK\) (c.g.c)

\( \Rightarrow A{\rm{D}} = EK\) (cạnh tương ứng).

c) Chứng minh tương tự ta có \(\Delta ANK = \Delta EN{\rm{D}}\) (c.g.c) \( \Rightarrow {\widehat A_1} = {\widehat E_1}\) (góc tương ứng)

\( \Rightarrow AK\) // DE (cặp góc so le trong bằng nhau).

d) Xét \(\Delta A{\rm{D}}K\) theo bất đẳng thức tam giác ta có \(A{\rm{D}} + AK > DK.\)

\(AD + DE > 2DN\)(đpcm).

Loigiaihay.com