Đề kiểm tra 45 phút (1 tiết) - Chương 2 + 3 - Đề số 1 - Đại số 10Đáp án và lời giải chi tiết Đề kiểm tra 45 phút (1 tiết) - Chương 2 + 3 - Đề số 1 - Đại số 10 Quảng cáo
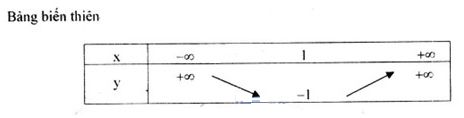
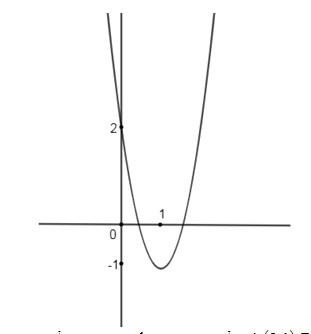
Đề bài Câu 1. a. Lập bảng biến thiên và vẽ đồ thị hàm số \(y = 3{x^2} - 6x + 2\) . b. Xác định a, b để đường thẳng \(y = ax + b\) đi qua hai điểm A(3;1), B(-3;-5). c. Xác định giao điểm của hai đồ thị trên. Câu 2. a. Giải và biện luận phương trình \({m^2}x - 3 = 9x + m\) theo tham số m. b. Giải phương trình \({{{x^2} - 2} \over x} + {x \over {{x^2} - 2}} = 2\) . Câu 3. Cho phương trình \(\left( {m - 1} \right){x^2} - 2mx + m + 2 = 0\) . a. Xác định m để phương trình có nghiệm. b. Với giá trị nào của m thì phương trình có hai nghiệm trái dấu? Lời giải chi tiết Câu 1. a.Xét hàm số \(y = 3{x^2} - 6x + 2\) Tập xác định \(D=R\) Đỉnh: \(I\left( {1; - 1} \right)\) Trục đối xứng \(x=1\) \(x = 0 \Rightarrow y = 2\) : Đồ thị cắt trục tung tại điểm (0;2). \(y = 0 \Rightarrow 3{x^2} - 6x + 2 = 0 \Rightarrow x = {{3 \pm \sqrt 3 } \over 3}\) . Đồ thị cắt trục hoành tại hai điểm \(\left( {{{3 \pm \sqrt 3 } \over 3};0} \right)\) Đồ thị b.Đường thẳng \(y = ax + b\) đi qua hai điểm \(A\left( {3;1} \right),B\left( { - 3; - 5} \right)\) khi và chỉ khi \(\left\{ \matrix{ 3a + b = 1 \hfill \cr - 3a - b = - 5 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ a = 1 \hfill \cr b = - 2 \hfill \cr} \right.\) Vậy đường thẳng có phương trình \(y = x - 2\) . c. Phương trình hoành độ giao điểm của hai đồ thị \(3{x^2} - 6x + 2 = x - 2 \Leftrightarrow 3{x^2} - 7x + 4 = 0 \Leftrightarrow \left[ \matrix{ x = 1 \hfill \cr x = {4 \over 3} \hfill \cr} \right.\) Vậy giao điểm của hai đồ thị là (1;-1) và \(\left( {{4 \over 3}; - {2 \over 3}} \right)\) . Câu 2. a.Ta có \({m^2}x - 3 = 9x + m \Leftrightarrow \left( {{m^2} - 9} \right)x = m + 3\) . Xét các trường hợp \({m^2} - 9 \ne 0 \Leftrightarrow m \ne \pm 3\) Phương trình có nghiệm duy nhất \(x = {{m + 3} \over {{m^2} - 9}} = {1 \over {m - 3}}\) . \(m= 3\): Phương trình trở thành \(0x= 6\). Phương trình vô nghiệm. m= -3:Phương trình trở thành 0x= 0. Phương trình nghiệm đúng với mọi Kết luận : \(m \ne \pm 3:{\rm{ x = }}\dfrac{1 } {m - 3}\) . m= 3: Phương trình vô nghiệm . b. Xét phương trình \(\dfrac{{{x^2} - 2}}{x} + \dfrac{x}{{{x^2} - 2}} = 2\) Điều kiện xác định: \(x \ne 0,x \ne \pm \sqrt 2 \) . Đặt \(t = \dfrac{{{x^2} - 2}}{x},{t^2} \ne 0\) . Phương trình trở thành \(t + \dfrac{1}{t} = 2 \Leftrightarrow {t^2} - 2t + 1 = 0 \) \(\Leftrightarrow t = 1\) (thỏa mãn điều kiện) Vậy \(\dfrac{{{x^2} - 2}}{x} = 1 \Leftrightarrow {x^2} - x - 2 = 0 \) \(\Leftrightarrow \left[ \matrix{ x = - 1 \hfill \cr x = 2 \hfill \cr} \right.\) (thỏa mãn điều kiện) Phương trình đã cho có hai nghiệm \(x= -1, x=2.\) Câu 3. a. Xét phương trình \(\left( {m - 1} \right){x^2} - 2mx + m + 2 = 0\) (1) \(m= 1\): Phương trình trở thành \( - 2x + 3 = 0\) . Phương trình có nghiệm \(x = \dfrac{3 }{ 2}\) . \(m \ne 1\) : Lập \(\Delta ' = {m^2} - \left( {m - 1} \right)\left( {m + 2} \right) = - m + 2\) . Phương trình có nghiệm khi và chỉ khi \(\Delta ' \ge 0 \Leftrightarrow - m + 2 \ge 0 \Leftrightarrow m \le 2\) . Kết luận: Phương trình (1) có hai nghiệm khi \(m \le 2\) . b. Phương trình (1) có hai nghiệm trái dấu khi và chỉ khi \(P < 0 \Leftrightarrow \dfrac{{n + 2}}{{m - 1}}< 0 \) \(\Leftrightarrow \left[ \matrix{ \left\{ \matrix{ m + 2 > 0 \hfill \cr m - 1 < 0 \hfill \cr} \right. \Leftrightarrow - 1 < m < 1 \hfill \cr \left\{ \matrix{ m + 2 < 0 \hfill \cr m + 1 > 0 \hfill \cr} \right.{\rm{ }} \hfill \cr} \right.\) Loigiaihay.com
|




















Danh sách bình luận