Đề kiểm tra 45 phút (1 tiết) - Chương 1 - Đề số 4 - Đại số 10

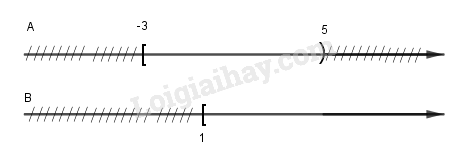
Đề bài

Câu I (3 điểm). Xét tính đúng, sai và lập mệnh đề phủ định của mỗi mệnh đề sau.

a) \(\forall n \in \mathbb{N}\) : 4n² chia hết cho n.

b) \(\forall x \in \mathbb{R}:{x^2} - 6x + 10 > 0\)

c) \(\exists x \in \mathbb{Q}\,:\,{x^2} - 7 \ne 7x\)

d) Tổng ba góc của một tam giác bằng \({180^0}\)

e) \(\sqrt 9 \) là số vô tỉ

f) Paris là thủ đô của nước Pháp

Câu II (3 điểm). Cho các tập hợp

\(\begin{array}{l}A = \left\{ { - 3;5;6} \right\}\\B = \left\{ {x \in \mathbb{R}:{x^2} - 4{\rm{x}} - 5 = 0} \right\}\\C = \left\{ {x \in \mathbb{N}:(x - 2)({x^2} + 5x - 6) = 0} \right\}\end{array}\)

1) Viết tập hợp B và C dưới dạng liệt kê các phần tử. Tìm \(A \cap B;\,\;A \cup C\)

2) Tìm \((A \cup B)\backslash C;\;(A\backslash B) \cap C\)

Câu III (3 điểm). Biểu diễn các tập sau trên trục số và tìm \(A \cap B;\;A \cup B\).

a) \(A = \left[ { - 3;5} \right)\) và \(B = \left[ {1; + \infty } \right)\)

b) \(A = \left\{ {x \in \mathbb{R}\,:\,x \le 3} \right\}\) và \(B = \left\{ {x \in \mathbb{R}\,:\,\,\left| x \right| > 2} \right\}\)

Câu IV (1 điểm). Cho hai tập hợp \(A = \left[ {a;a + 1} \right];\;B = \left[ {b;b + 2} \right]\). Các số a và b thỏa mãn điều kiện gì để \(A \cap B \ne \emptyset \)?

Lời giải chi tiết

Câu I (3 điểm). Xét tính đúng, sai và lập mệnh đề phủ định của mỗi mệnh đề sau.

a) \(\forall n \in \mathbb{N}\) : 4n² chia hết cho n.

Mệnh đề sai vì với \(n = 0\) thì không có số nào chia hết cho \(0\).

MĐ phủ định: \(\exists n \in \mathbb{N}:\) \(4{n^2}\) không chia hết cho \(n\).

b) \(\forall x \in \mathbb{R}:{x^2} - 6x + 10 > 0\)

Mệnh đề đúng vì:

\(\begin{array}{l}{x^2} - 6x + 10\\ = {x^2} - 6x + 9 + 1\\ = {\left( {x - 3} \right)^2} + 1 > 0,\forall x \in \mathbb{R}\end{array}\)

MĐ phủ định: \(\exists x \in \mathbb{R}:{x^2} - 6x + 10 \le 0\)

c) \(\exists x \in \mathbb{Q}\,:\,{x^2} - 7 \ne 7x\)

Mệnh đề đúng, chẳng hạn \(x = 0 \in \mathbb{Q}\) mà \({0^2} - 7 =  - 7 \ne 7.0 = 0\).

MĐ phủ định: \(\forall x \in \mathbb{Q}:{x^2} - 7 = 7x\).

d) Tổng ba góc của một tam giác bằng \({180^0}\)

MĐ đúng theo định lý tổng ba góc của một tam giác.

MĐ phủ định: Tổng ba góc của một tam giác không bằng \({180^0}\).

e) \(\sqrt 9 \) là số vô tỉ

MĐ sai vì \(\sqrt 9  = 3\) là số hữu tỉ.

MĐ phủ định: \(\sqrt 9 \) không là số vô tỉ.

f) Paris là thủ đô của nước Pháp.

MĐ đúng.

MĐ phủ định: Paris không là thủ đô của nước Pháp.

Câu II (3 điểm). Cho các tập hợp

\(\begin{array}{l}A = \left\{ { - 3;5;6} \right\}\\B = \left\{ {x \in \mathbb{R}:{x^2} - 4x - 5 = 0} \right\}\\C = \left\{ {x \in \mathbb{N}:(x - 2)({x^2} + 5x - 6) = 0} \right\}\end{array}\)

1) Viết tập hợp B và C dưới dạng liệt kê các phần tử. Tìm \(A \cap B;\,\;A \cup C\)

Ta có:

\(\begin{array}{l}{x^2} - 4x - 5 = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x = 5\end{array} \right.\\ \Rightarrow B = \left\{ { - 1;5} \right\}\\\left( {x - 2} \right)\left( {{x^2} + 5x - 6} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\{x^2} + 5x - 6 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2 \in \mathbb{N}\\x = 1 \in \mathbb{N}\\x =  - 6 \notin \mathbb{N}\end{array} \right.\\ \Rightarrow C = \left\{ {1;2} \right\}\\A = \left\{ { - 3;5;6} \right\},B = \left\{ { - 1;5} \right\},\\C = \left\{ {1;2} \right\}\\ \Rightarrow A \cap B = \left\{ 5 \right\}\\A \cup C = \left\{ {1;2; - 3;5;6} \right\}\end{array}\)

2) Tìm \((A \cup B)\backslash C;\;(A\backslash B) \cap C\)

\(\begin{array}{l}A \cup B = \left\{ { - 3; - 1;5;6} \right\}\\\left( {A \cup B} \right)\backslash C = \left\{ { - 3; - 1;5;6} \right\}\\A\backslash B = \left\{ { - 3;6} \right\}\\\left( {A\backslash B} \right) \cap C = \emptyset \end{array}\)

Câu III (3 điểm). Biểu diễn các tập sau trên trục số và tìm \(A \cap B;\;A \cup B\).

a) \(A = \left[ { - 3;5} \right)\) và \(B = \left[ {1; + \infty } \right)\)

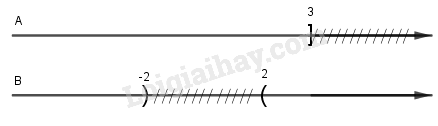
\(\begin{array}{l}A \cap B = \left[ {1;5} \right)\\A \cup B = \left[ { - 3; + \infty } \right)\end{array}\)

b) \(A = \left\{ {x \in \mathbb{R}\,:\,x \le 3} \right\}\) và \(B = \left\{ {x \in \mathbb{R}\,:\,\,\left| x \right| > 2} \right\}\)

\(\begin{array}{l}A = \left\{ {x \in \mathbb{R}:x \le 3} \right\} = \left( { - \infty ;3} \right]\\\left| x \right| > 2 \Leftrightarrow \left[ \begin{array}{l}x > 2\\x <  - 2\end{array} \right.\\ \Rightarrow B = \left( { - \infty ; - 2} \right) \cup \left( {2; + \infty } \right)\end{array}\)

\(\begin{array}{l}A \cap B = \left( { - \infty ; - 2} \right) \cup \left( {2;3} \right]\\A \cup B = \mathbb{R}\end{array}\)

Câu IV (1 điểm). Cho hai tập hợp \(A = \left[ {a;a + 1} \right];\;B = \left[ {b;b + 2} \right]\). Các số a và b thỏa mãn điều kiện gì để \(A \cap B \ne \emptyset \)

Ta có:

\(A \cap B = \emptyset \)\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{a + 1 < b}\\{a > b + 2}\end{array} \Leftrightarrow } \right.\left[ {\begin{array}{*{20}{c}}{b > a + 1}\\{b < a - 2}\end{array}} \right.\)

\( \Rightarrow A \cap B \ne \emptyset \) \( \Leftrightarrow \left\{ \begin{array}{l}b \le a + 1\\b \ge a - 2\end{array} \right.\) \( \Leftrightarrow a - 2 \le b \le a + 1\)

Vậy để \(A \cap B \ne \emptyset \) thì \(a - 2 \le b \le a + 1\).

Loigiaihay.com