Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Chương 3 - Hình học 7Giải Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Chương 3 - Hình học 7 Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
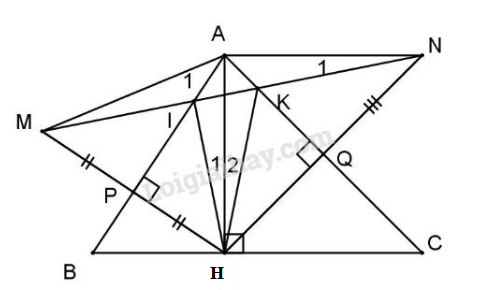
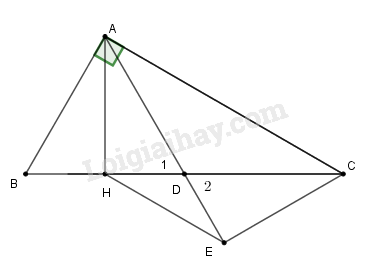
Đề bài Bài 1: Cho tam giác ABC nhọn. Đường cao AH, vẽ HP vuông góc với AB (P thuộc AB); trên tia đối của tia PH lấy \(PM = PH\) , vẽ HQ vuông góc với AC (Q thuộc AC). Trên tia đối của tia QH lấy \(QN = QH\). Nối M với N đường thẳng MN cắt AB, AC theo thứ tự tại Ivà K. Chứng minh: Bài 2: Cho tam giác ABC vuông ở A có \(\widehat C = {30^0}\), đường cao AH. Trên đoạn HC lấy điểm D sao cho \(H{\rm{D}} = HB\). Từ C kẻ CE vuông góc với AD. Chứng minh: a) \(\Delta AB{\rm{D}}\) là tam giác đều; b) \(AH = CE;\) c) EH // AC. LG bài 1 Phương pháp giải: Trong tam giác cân đường cao đồng thời là trung tuyến Trong tam giác cân đường cao đồng thời là đường trung trực Điểm thuộc đường trung trực của 1 đoạn thẳng thì cách đều 2 đầu mút Lời giải chi tiết:
a) Ta có \(PH \bot AB\) (gt), \(PM = PH\) (gt). Do đó \(\Delta MAH\) có đường cao AP đồng thời là đường trung tuyến nên \(\Delta AMH\) cân tại A \( \Rightarrow AM = AH.\) b) AMH cân tại A nên đường cao AP cũng đồng thời là đường trung trực, mà I thuộc AP nên \(IM = IH\); lại có \(AM = AH\) (cmt). Do đó \(\Delta AIM = \Delta AIH\) (c.c.c) \( \Rightarrow {\widehat M_1} = {\widehat H_1}.\) Chứng minh tương tự ta có \({\widehat N_1} = {\widehat H_2}\), mà \({\widehat M_1} = {\widehat N_1}\) (\(\Delta AMN\) cân). \( \Rightarrow {\widehat H_1} = {\widehat H_2}\) hay HA là tia phân giác của \(\widehat {IHK}\). LG bài 2 Phương pháp giải: Trong tam giác cân đường trung tuyến đồng thời là đường cao
Nếu 1 đường thẳng cắt hai đường thẳng cho trước, trong các cặp góc tạo thành có 1 cặp góc so le trong bằng nhau thì 2 đường thẳng đó song song Lời giải chi tiết:
a) \(\Delta AB{\rm{D}}\) có đường cao AH đồng thời là đường trung tuyến nên \(AB{\rm{D}}\) cân. Có \(\widehat B = {60^0}\) (vì \(\widehat C = {30^0}\) (gt)). Do đó \(\Delta AB{\rm{D}}\) đều. b) \(\Delta AB{\rm{D}}\) đều (cmt) \( \Rightarrow \widehat {BA{\rm{D}}} = {60^0} \Rightarrow \widehat {CA{\rm{D}}} = \widehat C = {30^0}.\) Do đó \(\Delta A{\rm{D}}C\) cân tại D \( \Rightarrow DA = DC.\) Xét hai tam giác vuông AHD và CED có: +) \(DA = DC\) (cmt); +) \({\widehat D_1} = {\widehat D_2}\) (đđ); Vậy \(\Delta AH{\rm{D}} = \Delta CE{\rm{D}}\) (cạnh huyền-góc nhọn) \( \Rightarrow AH = CE.\) c) \(\Delta AH{\rm{D}} = \Delta CE{\rm{D}}\)(cmt) \( \Rightarrow H{\rm{D}} = E{\rm{D}}\) (cạnh tương ứng). Do đó \(\Delta DHE\) cân tại D. Mặt khác \(\Delta A{\rm{D}}C\) cân tại D, mà hai tam giác cân này chung đỉnh D \( \Rightarrow \widehat {CHE} = \widehat {ACB} = {30^0}.\) \( \Rightarrow \) EH // AC (cặp góc so le trong bằng nhau). Loigiaihay.com
|




















Danh sách bình luận