Đề kiểm tra 15 phút - Đề số 3 - Bài 6 - Chương 2 - Hình học 8

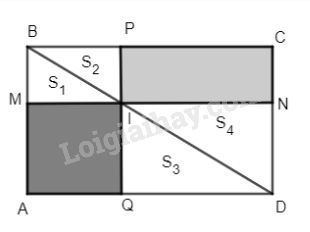
Đề bài

Cho hình chữ nhật ABCD, từ M bất kì trên AB, kẻ đường thẳng song song với BC cắt CD tại N và đường chéo BD tại I. Qua I kẻ đường thẳng song song với AB cắt hai cạnh BC và AD lần lượt tại P và Q. Chứng minh rằng hai hình chữ nhật MIQA và NIPC có cùng diện tích.

Lời giải chi tiết

 

Các tứ giác BPIM, INQD, PINC, MIQA, ABCD là các hình chữ nhật.

Ta có \(\Delta ABD = \Delta CDB\left( {c.g.c} \right)\)

\( \Rightarrow {S_{ABD}} = {S_{CBD}}\left( {c.g.c} \right)\)

Tương tự \({S_1} = {S_2},{S_3} = {S_4}.\)

Do đó: \({S_{ABD}} - \left( {{S_1} + {S_2}} \right) = {S_{CDB}} - \left( {{S_1} + {S_4}} \right)\)

Hay \({S_{MIQA}} = {S_{NIPC}}.\)

Loigiaihay.com