Đề kiểm tra 15 phút - Đề số 4 - Bài 6 - Chương 2 - Hình học 8Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 6 - Chương 2 - Hình học 8 Quảng cáo
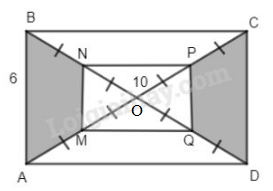
Đề bài Cho hình chữ nhật ABCD có AB = 6cm, AC = 10 cm. Gọi O là giao điểm hai đường chéo AC và BD và M, N, P, Q lần lượt là trung điểm của OA, OB, OC, OD. a) Tính \({S_{MNPQ}}.\) b) Chứng minh rằng: \({S_{AMNB}} = {S_{CPQD}}.\) Phương pháp giải - Xem chi tiết Sử dụng: Tứ giác có cặp cạnh đối song song và bằng nhau là hình bình hành Hình bình hành có 1 góc vuông là hình chữ nhật Diện tích hình chữ nhật bằng tích chiều dài và chiều rộng Lời giải chi tiết a) Ta có MN và PQ lần lượt là các đường trung bình của các tam giác AOB và COD mà \(AB// CD\) và AB = CD nên \(MN// PQ\) và MN = PQ. Tương tự \(NP//BC\) mà \(AB \bot BC\) nên \(MN \bot NP.\) Do đó MNPQ là hình chữ nhật. Trong \(\Delta ABC\) ta có: \(BC = \sqrt {A{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} \)\(\,= 8\left( {cm} \right)\) (định lý py – ta – go) Nên \(MN = {1 \over 2}AB = 3cm,\) \(NP = {1 \over 2}BC = 4cm\) Vậy \({S_{MNPQ}} = MN.NP = 3.4 = 12\left( {c{m^2}} \right)\) b) Vì OB=OD=OA=OC và AB=CD nên \(\Delta AOB = \Delta COD\left( {c.c.c} \right),\) tương tự \(\Delta MON = \Delta POQ.\) Do đó: \({S_{AOB}} = {S_{COD}}\) và \({S_{MON}} = {S_{POQ}}\) \( \Rightarrow {S_{AOB}} - {S_{MON}} = {S_{COD}} - {S_{POQ}}\) hay \({S_{AMNB}} = {S_{CPQD}}.\) Loigiaihay.com
|




















Danh sách bình luận