Đề kiểm tra 15 phút - Đề số 1 - Bài 4,5 - Chương 1 - Hình học 8Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 4,5 - Chương 1 - Hình học 8 Quảng cáo
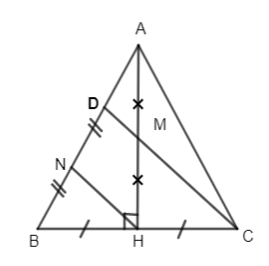
Đề bài Cho \(\Delta ABC\) cân tại A. Gọi M là trung điểm của đường cao AH. D là giao điểm của CM và AB. a) Gọi N là trung điểm của BD. Chứng minh rằng \(HN\parallel DC.\) b) Chứng minh \(AD = {1 \over 3}AB.\) Phương pháp giải - Xem chi tiết Sử dụng: - Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác. - Định lí : Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba. - Định lí : Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy. Lời giải chi tiết
a) \(\Delta ABC\) cân tại A nên đường cao AH đồng thời là đườg trung tuyến, hay H là trung điểm của BC. N là trung điểm của BD nên HN là đường trung bình của \(\Delta BCD \Rightarrow HN// DC.\) b) Ta có N là trung điểm của BD (gt) hay NB = ND (1) Mặt khác M là trung điểm của AH (gt), \(CD// NH\) (cmt) hay \(MD// NH\) Do đó DM là đường trung bình của \(\Delta ANH \Rightarrow D\) là trung điểm của AN Hay ND = AD (2) Từ (1) , (2) suy ra AD = DN = NB hay \(AD =\dfrac {1 }{3}AB.\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
