Đề kiểm tra 15 phút - Đề số 1 - Bài 3 - Chương 3 – Hình học 7Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 3 - Chương 3 – Hình học 7 Quảng cáo
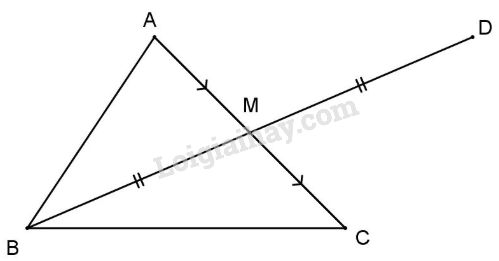
Đề bài Cho tam giác ABC, M là trung điểm cạnh AC. Trên tia đối của tia MB lấy điểm sao cho \(M{\rm{D}} = MB\). Chứng minh: a) \(\Delta MAB = \Delta MC{\rm{D}}\); b) \(BM < \dfrac{{AB + BC}}{2}\). Phương pháp giải - Xem chi tiết +Trong tam giác, độ dài 1 cạnh luôn nhỏ hơn tổng độ dài 2 cạnh còn lại Lời giải chi tiết
a) Xét \(\Delta MAB\) và \(\Delta MC{\rm{D}}\) có: +) \(MA = MC\) (gt); +) \(\widehat {AMB} = \widehat {CM{\rm{D}}}\) (đối đỉnh); +) \(MB = M{\rm{D}}\) (gt). Do đó \(\Delta MAB = \Delta MC{\rm{D}}\) (c.g.c). b) Xét \(\Delta BC{\rm{D}}\) theo bất đẳng thức tam giác ta có \(B{\rm{D}} < C{\rm{D}} + BC,\) mà \(B{\rm{D}} = 2BM\) và \(C{\rm{D}} = AB\) (cmt) \( \Rightarrow 2BM < AB + BC\) \(\Rightarrow BM < \dfrac{{AB + BC} }{ 2}.\) Loigiaihay.com
|