Câu hỏi trắc nghiệm chương III

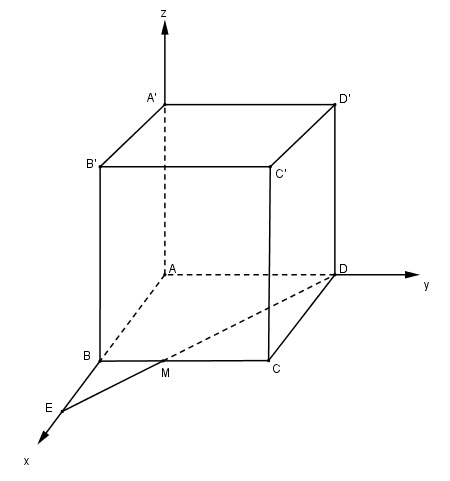
Câu 1

Cho ba điểm M(2; 0; 0), N(0; - 3; 0), P(0; 0; 4). Nếu MNPQ là một hình bình hành thì tọa độ điểm Q là:

(A) (-2; -3; 4)                      (B) (3; 4; 2)

(C) (2; 3; 4)                         (D) (-2; -3; -4)

Lời giải chi tiết:

MNPQ là hình bình hành

$\Leftrightarrow \overrightarrow {MN} = \overrightarrow {QP}$ $\Leftrightarrow \left\{ \matrix{ 0 - 2 = 0 - {x_Q} \hfill \cr  - 3 - 0 = 0 - {y_Q} \hfill \cr  0 - 0 = 4 - {z_Q} \hfill \cr} \right.$ $\Leftrightarrow \left\{ \matrix{ {x_Q} = 2 \hfill \cr  {y_Q} = 3 \hfill \cr  {z_Q} = 4 \hfill \cr} \right.$

Vậy Q(2; 3; 4).

Chọn (C).

Câu 2

Cho ba điểm $A\left( {1;2;0} \right)\,\,,\,\,B\left( {1;0; - 1} \right)\,\,,\,\,C\left( {0; - 1;2} \right).$ Tam giác ABC là:

(A) Tam giác cân đỉnh A;       

(B) Tam giác vuông đỉnh A;

(C) Tam giác đều;

(D) Không phải như (A), (B), (C).

Lời giải chi tiết:

Ta có 

$\eqalign{ & AB = \sqrt {{{\left( {1 - 1} \right)}^2} + {{\left( {0 - 2} \right)}^2} + {{\left( {-1 - 0} \right)}^2}} = \sqrt 5 \cr  & AC = \sqrt {{{\left( {0 - 1} \right)}^2} + {{\left( { - 1 - 2} \right)}^2} + {{\left( {2 - 0} \right)}^2}} = \sqrt {14} \cr  & BC = \sqrt {{{\left( {0 - 1} \right)}^2} + {{\left( { - 1 - 0} \right)}^2} + {{\left( {2 + 1} \right)}^2}} = \sqrt {11} \cr  & \Rightarrow A{B^2} + B{C^2} > A{C^2} \cr}$

$AC>BC>AB$

Chọn (D)

Câu 3

Cho tam giác ABC có A=(1;0;1), B=(0;2;3), C(2;1;0). Độ dài đường cao tam giác kẻ từ C là:

(A) $\sqrt {26}$          (B) ${{\sqrt {26} } \over 2}$

(C) ${{\sqrt {26} } \over 3}$           (D) 26

Lời giải chi tiết:

Ta có: $\overrightarrow {AB}  = \left( { - 1;2;2} \right),\overrightarrow {AC}  = \left( {1;1; - 1} \right)$

Khoảng cách từ C đến đường thẳng AB là:  $h = {{\left| {\left[ {\overrightarrow {AC} ,\overrightarrow {AB} } \right]} \right|} \over {\left| {\overrightarrow {AB} } \right|}} = {{\sqrt {26} } \over 3}.$

Chọn (C).

Câu 4

Ba đỉnh của một hình bình hành có tọa độ là $\left( {1;1;1} \right)\,\,;\,\,\left( {2;3;4} \right)\,\,;\,\,\left( {6;5;2} \right).$ Diện tích hình bình hành đó bằng:

(A) $2\sqrt {83}$         (B) $\sqrt {83}$

(C) 83           (D) ${{\sqrt {83} } \over 2}$

Lời giải chi tiết:

A(1; 1; 1), B(2; 3; 4), C(6; 5; 2).

${S_{ABCD}} = 2{S_{ABC}} = \left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]} \right|$ $= 2\sqrt {83} .$

Chọn (A).

Câu 5

Cho $A\left( {1;0;0} \right)\,\,;\,\,B\left( {0;1;0} \right)\,\,;\,\,C\left( {0;0;1} \right)$ và $D\left( { - 2;1; - 1} \right)$. Thể tích của tứ diện ABCD là:

(A) 1             (B) 2          (C) ${1 \over 3}$            (D) ${1 \over 2}$

Lời giải chi tiết:

$\eqalign{ & \overrightarrow {AB} \left( { - 1;1;0} \right),\overrightarrow {AC} \left( { - 1;0;1} \right) \cr  & \Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right] = \left( {\left| \matrix{ 1\,\,\,\,\,\,\,\,0 \hfill \cr  0\,\,\,\,\,\,\,\,1 \hfill \cr} \right|;\left| \matrix{ 0\,\,\,\, - 1 \hfill \cr  1\,\,\,\,\, - 1 \hfill \cr} \right|;\left| \matrix{ - 1\,\,\,\,\,1 \hfill \cr  - 1\,\,\,\,0 \hfill \cr} \right|} \right) \cr &= \left( {1;1;1} \right) \cr  & \overrightarrow {AD} \left( { - 3;1; - 1} \right) \cr  & \Rightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AD} = 1.\left( { - 3} \right) + 1.1 + 1.\left( { - 1} \right) = - 3 \cr  & \Rightarrow {V_{ABCD}} = {1 \over 6}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AD} } \right| = {3 \over 6} = {1 \over 2}. \cr}$

Chọn D

Câu 6

Cho $A\left( { - 1; - 2;4} \right)\,\,;\,\,B\left( { - 4; - 2;0} \right)\,\,;\,\,C\left( {3; - 2;1} \right)$ và $D\left( {1;1;1} \right)$. Độ dài đường cao của tứ diện ABCD kẻ từ đỉnh D là:

(A) 3                 (B) 1                   (C) 2                  (D) ${1 \over 2}$

Lời giải chi tiết:

Độ dài đường cao của tứ diện ABCD kẻ từ D là khoảng cách từ D đến mp(ABC).
Ta có: 

$\eqalign{ & \overrightarrow {AB} \left( { - 3;0; - 4} \right),\overrightarrow {AC} \left( {4;0; - 3} \right) \cr  & \Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right] = \left( {\left| \matrix{ 0\,\,\,\,\,\,\, - 4 \hfill \cr  0\,\,\,\,\,\,\,\, - 3 \hfill \cr} \right|;\left| \matrix{ - 4\,\,\, - 3 \hfill \cr  - 3\,\,\,\,\,\,\,4 \hfill \cr} \right|;\left| \matrix{ - 3\,\,\,\,0 \hfill \cr  4\,\,\,\,\,\,0 \hfill \cr} \right|} \right) = \left( {0; - 25;0} \right) = - 25\left( {0;1;0} \right) \cr}$

Suy ra mặt phẳng (ABC) đi qua A và nhận $\overrightarrow n  = \left( {0;1;0} \right)$ là vectơ pháp tuyến.
Phương trình mặt phẳng (ABC): $y + 2 = 0$.

$\Rightarrow h = d\left( {D;\left( {ABC} \right)} \right) = {{\left| {1 + 2} \right|} \over {\sqrt 1 }} = 3.$
Chọn (A).

Câu 7

Cho bốn điểm $A\left( {1;1;1} \right)\,\,,\,\,B\left( {1;2;1} \right)\,\,,C\left( {1;1;2} \right)$ và $D\left( {2;2;1} \right).$ Tâm I mặt cầu ngoại tiếp tứ diện ABCD là:

(A) $\left( {{3 \over 2}, - {3 \over 2},{3 \over 2}} \right)$                 (B) $\left( {{3 \over 2},{3 \over 2},{3 \over 2}} \right)$

(C) $\left( {3;3;3} \right)$                          (D) $\left( {3; - 3;3} \right).$

Lời giải chi tiết:

Phương trình mặt cầu ngoại tiếp tứ diện ABCD có dạng

${x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\,\,\left( 1 \right)$

Thay tọa độ của A, B, C, D vào (1) ta được hệ phương trình

$\left\{ \matrix{ 3 - 2a - 2b - 2c + d = 0 \hfill \cr  6 - 2a - 4b - 2c + d = 0 \hfill \cr  6 - 2a - 2b - 4c + d = 0 \hfill \cr  9 - 4a - 4b - 2c + d = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ a = b = c = {3 \over 2} \hfill \cr  d = 6 \hfill \cr} \right. \Rightarrow I\left( {{3 \over 2};{3 \over 2};{3 \over 2}} \right)$.

Chọn (B).

Câu 8

Bán kính mặt cầu tâm I(3;3;-4) tiếp xúc với trục Oy bằng:

(A) 5                  (B) 4                (C) $\sqrt 5$                   (D) ${5 \over 2}.$

Lời giải chi tiết:

Hình chiếu của I trên trục Oy là I’(0; 3; 0).

Khoảng cách từ điểm I đến trục Oy bằng $R = II' = \sqrt {{(-3)^2} + {4^2}}  = 5.$

Chọn (A).

Câu 9

Mặt cầu tâm $I\left( {2;1; - 1} \right)$ tiếp xúc với mặt phẳng tọa độ (Oyz) có phương trình là:

(A) ${\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 4;$

(B) ${\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 1;$

(C) ${\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 1} \right)^2} = 4;$

(D) ${\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 2.$

Lời giải chi tiết:

Mp(Oyz) có phương trình x = 0.

Khoảng cách từ I đến mp(Oyz) là $R = {{\left| 2 \right|} \over {\sqrt {{1^2} + {0^2} + {0^2}} }} = 2.$

Vậy phương trình mặt cầu cần tìm là:

${\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 4$

Chọn (A).

Câu 10

Cho ba điểm $A\left( {1;1;3} \right),\,\,B\left( { - 1;3;2} \right)$ và $C\left( { - 1;2;3} \right).$Mặt phẳng (ABC) có phương trình là:

(A) $x + 2y + 2z - 3 = 0$         

(B) $x - 2y + 3z - 3 = 0;$

(C) $x + 2y + 2z - 9 = 0;$     

(D) ${x^2} + 2y + 2z + 9 = 0$.

Lời giải chi tiết:

Mp(ABC) có vectơ pháp tuyến $\overrightarrow n  = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {1;2;2} \right).$

Vậy phương trình mặt phẳng (ABC) là:  $x + 2y + 2z - 9 = 0$
Chọn (C).

Câu 11

Cho ba điểm $A\left( {1;0;0} \right),\,\,B\left( {0;2;0} \right),\,\,C\left( {0;0;3} \right).$ Phương trình nào sau đây không phải là phương trình mặt phẳng (ABC)?

(A) $x + {y \over 2} + {z \over 3} = 1;$

(B) $6x + 3y + 2z - 6 = 0;$

(C) $6x + 3y + 2z + 6 = 0;$ 

(D) $12x + 6y + 4z - 12 = 0.$

Phương pháp giải:

Lời giải chi tiết:

Mp(ABC) ${x \over 1} + {y \over 2} + {z \over 3} = 1$
Chọn (C).

Câu 12

Cho hai điểm $A\left( {1;3; - 4} \right)$ và $B\left( { - 1;2;2} \right)$. Phương trình mặt phẳng trung trực của đoạn AB là:

(A) $4x + 2y - 12z - 17 = 0;$ 

(B) $4x + 2y + 12z - 17 = 0;$

(C) $4x - 2y - 12z - 17 = 0;$ 

(D) $4x - 2y + 12z + 17 = 0.$

Lời giải chi tiết:

$\overrightarrow {AB}  = \left( { - 2; - 1;6} \right).$
Trung điểm AB là $I\left( {0;{5 \over 2}; - 1} \right)$.
Phương trình mặt phẳng tung trực của AB đi qua I và có vectơ pháp tuyến là $\overrightarrow n  = \overrightarrow {AB}$ nên có dạng: $- 2\left( {x - 0} \right) - \left( {y - {5 \over 2}} \right) + 6\left( {z + 1} \right) = 0 \Leftrightarrow 4x + 2y - 12z - 17 = 0.$
Chọn (A).

Câu 13

Cho A(a; 0; 0), B(0; b; 0), C(0; 0; c), a, b, c là những số dương thay đổi sao cho ${1 \over a} + {1 \over b} + {1 \over c} = 2.$ Mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ là:

(A) (1; 1; 1)                    (B) (2; 2; 2)

(C) $\left( {{1 \over 2},{1 \over 2},{1 \over 2}} \right)$        (D) $\left( { - {1 \over 2}, - {1 \over 2}, - {1 \over 2}} \right)$.

Lời giải chi tiết:

Phương trình mp(ABC): ${x \over a} + {y \over b} + {z \over c} = 1.$
Mp(ABC) đi qua điểm $\left( {{1 \over 2};{1 \over 2};{1 \over 2}} \right)$ cố định. 
Chọn (C).

Câu 14

Cho điểm $A\left( { - 1;2;1} \right)$ và hai mặt phẳng $\left( P \right):2x + 4y - 6z - 5 = 0$ và $\left( Q \right):x + 2y - 3z = 0.$ Mệnh đề nào sau đây là đúng?

(A) Mp(Q) qua A và song song với (P);

(B) Mp(Q) không qua A và song song với (P);

(C) Mp(Q) qua A và không song song với (P);

(D) Mp(Q) không qua A và không song song với (P).

Lời giải chi tiết:

$A \in \left( Q \right)$ và (Q) // (P).
Chọn (A).

Câu 15

Cho điểm $A\left( {1;2; - 5} \right)$. Gọi M, N, P là hình chiếu của A lên ba trục Ox, Oy, Oz. Phương trình mặt phẳng (MNP) là:

(A) $x + {y \over 2} - {z \over 5} = 1;$          (B) $x + {y \over 2} + {z \over 5} = 1;$

(C) $x + {y \over 2} - {z \over 5} = 0;$            (D) $x + {y \over 2} - {z \over 5} + 1 = 0.$

Lời giải chi tiết:

Ta có $M\left( {1;0;0} \right);N\left( {0;2;0} \right),P\left( {0;0; - 5} \right).$
Mp(MNP): ${x \over 1} + {y \over 2} + {z \over { - 5}} = 1.$
Chọn (A).

Câu 16

Cho mặt cầu $\left( S \right):{x^2} + {y^2} + {z^2} - 2\left( {x + y + z} \right) - 22 = 0$ và mặt phẳng (P): $3x - 2y + 6z + 14 = 0.$ Khoảng cách từ tâm I của mặt cầu (S) tới mặt phẳng (P) là:

(A 1              (B) 2                 (C) 3                    (D) 4.

Lời giải chi tiết:

Tâm I(1; 1; 1).
$d\left( {I;\left( P \right)} \right) = {{\left| {3 - 2 + 6 + 14} \right|} \over {\sqrt {9 + 4 + 36} }} = 3.$
Chọn (C).

Câu 17

Mặt phẳng (P) cắt ba trục Ox, Oy, Oz tại A, B, C, trọng tâm tam giác ABC là $G\left( { - 1; - 3;2} \right)$. Phương trình mặt phẳng (P) là:

(A) $x + y - z - 5 = 0;$ 

(B) $2x - 3y - z - 1 = 0;$

(C) $x + 3y - 2z + 1 = 0;$ 

(D) $6x + 2y - 3z + 18 = 0.$

Lời giải chi tiết:

Giả sử A(a; 0; 0), B(0; b; 0), C(0; 0; c) thì $G\left( {{a \over 3};{b \over 3};{c \over 3}} \right) \Rightarrow a =  - 3,\,\,b =  - 9,\,\,c = 6.$
Mp(ABC): ${x \over { - 3}} + {y \over { - 9}} + {z \over 6} = 1 \Leftrightarrow 6x + 2y - 3z + 18 = 0.$
Chọn (D).

Câu 18

Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng 1. Gọi M là trung điểm cạnh BC. Tính khoảng cách từ A tới mặt phẳng (A’MD).

Một học sinh làm như sau:

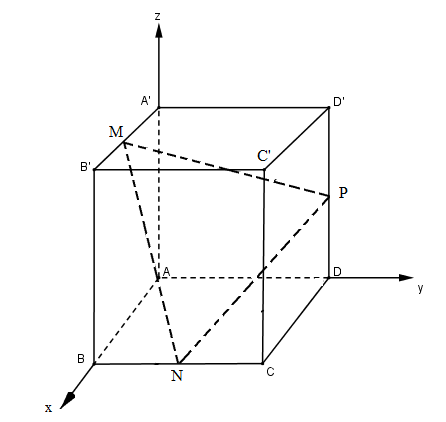
Bước 1: Chọn hệ trục tọa độ như hình vẽ. Kéo dài DM cắt AB tại E. Khi đó

$\eqalign{ & A = \left( {0;0;0} \right)\,,\,\,\,\,\,\,\,\,\,\,\,\,E = \left( {2;0;0} \right) \cr  & D = \left( {0;1;0} \right)\,,\,\,\,\,\,\,\,\,\,\,\,\,\,A' = \left( {0;0;1} \right) \cr}$

Bước 2. Viết phương trình mặt phẳng (A’MD):

${x \over 2} + {y \over 1} + {z \over 1} = 1 \Leftrightarrow x + 2y + 2z - 2 = 0.$
Bước 3. Khoảng cách $d\left( {A;\left( {A'MD} \right)} \right) = {{\left| { - 2} \right|} \over {\sqrt {1 + 4 + 4} }} = {2 \over 3}.$

Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?

(A) Đúng;                              (B) Sai ở bước 1;

(C) Sai ở bước 2;                (D) Sai ở bước 3.

Lời giải chi tiết:

Chon A

Câu 19

Cho hai điểm $A\left( {1; - 1;5} \right)$ và $B\left( {0;0;1} \right)$. Mặt phẳng (P) chứa A, B và song song với Oy có phương trình là:

(A) $4x - z + 1 = 0$ 

(B) $4x + y - z + 1 = 0$

(C) $2x + z - 5 = 0$

(D) $y + 4z - 1 = 0.$

Lời giải chi tiết:

Mp(P) qua A và có vectơ pháp tuyến $\overrightarrow n  = \left[ {\overrightarrow {AB} ;\overrightarrow j } \right]$ với $\overrightarrow j  = \left( {0;1;0} \right).$

$\eqalign{ & \overrightarrow {AB} \left( { - 1;1; - 4} \right) \cr  & \Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow j } \right] = \left( {\left| \matrix{ 1\,\,\,\,\, - 4 \hfill \cr  1\,\,\,\,\,\,\,\,0 \hfill \cr} \right|;\left| \matrix{ - 4\,\,\, - 1 \hfill \cr  0\,\,\,\,\,\,\,\,\,0 \hfill \cr} \right|;\left| \matrix{ - 1\,\,\,\,1 \hfill \cr  0\,\,\,\,\,\,1 \hfill \cr} \right|} \right) = \left( {4;0; - 1} \right) \cr}$

Chon A

Câu 20

Mặt phẳng (P) chứa trục Oz và điểm $A\left( {2; - 3;5} \right)$ có phương trình là:

(A) $2x + 3y = 0;$                    (B) $2x - 3y = 0;$

(C) $3x + 2y = 0;$                   (D) $3x - 2y + z = 0.$

Lời giải chi tiết:

Mp(P) qua O và có vectơ pháp tuyến $\overrightarrow n  = \left[ {\overrightarrow {OA} ,\overrightarrow k } \right]$ với $\overrightarrow k  = \left( {0;0;1} \right).$

$\eqalign{ & \overrightarrow {OA} \left( {2; - 3;5} \right) \cr  & \Rightarrow \left[ {\overrightarrow {OA} ;\overrightarrow k } \right] = \left( {\left| \matrix{ - 3\,\,\,\,5 \hfill \cr  0\,\,\,\,\,\,\,\,1 \hfill \cr} \right|;\left| \matrix{ 5\,\,\,\,\,\,2 \hfill \cr  1\,\,\,\,\,\,\,0 \hfill \cr} \right|;\left| \matrix{ 2\,\,\,\, - 3 \hfill \cr  0\,\,\,\,\,\,\,0 \hfill \cr} \right|} \right) = \left( { - 3; - 2;0} \right) \cr}$

Chọn C

Câu 21

Cho mặt phẳng (P) có phương trình $x - y - 1 = 0.$ Điểm $H\left( {2; - 1; - 2} \right)$ là hình chiếu vuông góc của gốc tọa độ O trên một mặt phẳng (Q). Góc giữa hai mặt phẳng (P) và (Q) là:

(A) ${30^0}$               (B) ${45^0}$           (C) ${60^0}$                (D) ${90^0}$

Lời giải chi tiết:

mp(Q) có vectơ pháp tuyến $\overrightarrow m  = \overrightarrow {OH}  = \left( {2; - 1; - 2} \right)$
Mp(P) có vectơ pháp tuyến $\overrightarrow n  = \left( {1; - 1;0} \right)$.
$\varphi$ là góc giữa hai mặt phẳng (P) và (Q) thì:
$\cos \varphi  = {{\left| {\overrightarrow m .\overrightarrow n } \right|} \over {\left| {\overrightarrow m } \right|.\left| {\overrightarrow n } \right|}} = {{\left| {2 + 1} \right|} \over {\sqrt {4 + 1 + 4} .\sqrt {1 + 1 + 0} }} = {1 \over {\sqrt 2 }} \Rightarrow \varphi  = {45^0}.$
Chọn (B).

Câu 22

Cho điểm A(1; 2; 3) và đường thẳng $d:{x \over 3} = {{y - 1} \over 4} = z + 3$. Phương trình mặt phẳng (A,d) là:

(A) $23x + 17y - z + 14 = 0$

(B) $23x - 17y - z + 14 = 0;$

(C) $23x + 17y + z - 60 = 0;$ 

(D) $23x - 17y + z - 14 = 0.$

Lời giải chi tiết:

d có vectơ chỉ phương $\overrightarrow u  = \left( {3,4,1} \right)$ và đi qua $M\left( {0,1, - 3} \right).$
Mp(A, d) qua A và có vectơ pháp tuyến $\overrightarrow n  = \left[ {\overrightarrow {AM} ,\overrightarrow u } \right].$

Vậy phương trình mặt phẳng cần tìm là:

$23x - 17y - z + 14 = 0$
Chọn (B).

Câu 23

Cho hai đường thẳng

${d_1}:{{x - 1} \over 1} = {y \over 2} = {{z - 3} \over 3}\,\,;\,\,\,{d_2}:\left\{ \matrix{ x = 2t \hfill \cr  y = 1 + 4t \hfill \cr  z = 2 + 6t. \hfill \cr} \right.$

Khẳng định nào sau đây là đúng?

(A) ${d_1},{d_2}$ cắt nhau;                         (B) ${d_1},{d_2}$ trùng nhau;

(C) ${d_1}//{d_2}$;                                    (D) ${d_1},{d_2}$ chéo nhau.

Lời giải chi tiết:

${d_1},{d_2}$ có cùng vectơ chỉ phương $\overrightarrow u  = \left( {1,2,3} \right)$ và  $A\left( {1,0,3} \right) \in {d_1},$ nhưng $A \notin {d_2}.$ Vậy ${d_1}$ // ${d_2}$
Chọn (C).

Câu 24

Cho mặt phẳng $\left( \alpha  \right):x + 3y + z + 1 = 0$ và đường thẳng 

$d:\left\{ \matrix{ x = 1 + t \hfill \cr  y = 2 - t \hfill \cr  z = 2 - 3t. \hfill \cr} \right.$ Tọa độ giao điểm A của d và $\left( \alpha  \right)$ là:

(A) A(3; 0; 4)                                   (B) $A\left( {3; - 4;0} \right)$

(C) $A\left( { - 3;0;4} \right)$                             (D) $A\left( {3;0; - 4} \right)$.

Lời giải chi tiết:

Thay x, y, z từ d vào $\left( \alpha  \right)$ ta có: $1 + t + 3\left( {2 - t} \right) + 2 - 3t + 1 = 0 \Leftrightarrow t = 2.$
Vậy $A\left( {3,0, - 4} \right).$
Chọn (D).

Câu 25

Cho đường thẳng

$d:\left\{ \matrix{ x = 2t \hfill \cr  y = 1 - t \hfill \cr  z = 2 + t. \hfill \cr} \right.$

Phương trình nào sau đây cũng là phương trình của đường thẳng d?
(A) 

$\left\{ \matrix{ x = 2 - 2t \hfill \cr  y = - t \hfill \cr  z = 3 + t\,; \hfill \cr} \right.$

(B) 

$\left\{ \matrix{ x = 4 - 2t \hfill \cr  y = - 1 + t \hfill \cr  z = 4 - t\,; \hfill \cr} \right.$

(C) 

$\left\{ \matrix{ x = 4 + 2t \hfill \cr  y = 1 - t \hfill \cr  z = 4 + t\,; \hfill \cr} \right.$

(D) 

$\left\{ \matrix{ x = 2t \hfill \cr  y = 1 + t \hfill \cr  z = 2 + t\,. \hfill \cr} \right.$

Lời giải chi tiết:

d đi qua $M\left( {4, - 1,4} \right)$ có vectơ chỉ phương $\overrightarrow u  = \left( {2; - 1;1} \right).$
Chọn (B).

Câu 26

Cho hai điểm $A\left( {2;3; - 1} \right),B\left( {1;2;4} \right)$ và ba phương trình sau:

$\left( I \right)\,\,\left\{ \matrix{ x = 2 - t \hfill \cr  y = 3 - t \hfill \cr  z = - 1 + 5t\,; \hfill \cr} \right.\,\,\,\,\,\,\,\,\,\,\,\,\left( {II} \right)\,\,{{x - 2} \over 1} = {{y - 3} \over 1} = {{z + 1} \over { - 5}};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {III} \right)\,\,\left\{ \matrix{ x = 1 - t \hfill \cr  y = 2 - t \hfill \cr  z = 4 + 5t\,. \hfill \cr} \right.$

Mệnh đề nào sau đây là đúng?

(A) Chỉ có (I) là phương trình của đường thẳng AB;

(B) Chỉ có (III) là phương trình của đường thẳng AB;

(C) Chỉ có (I) và (II) là phương trình của đường thẳng AB;

(D) Cả (I), (II) và (III) là phương trình của đường thẳng AB.

Lời giải chi tiết:

Đường thẳng AB có vectơ chỉ phương $\overrightarrow {AB}  = \left( { - 1, - 1,5} \right).$
Chọn (D).

Câu 27

Cho ba điểm A(1; 3; 2), B(1; 2; 1), C(1; 1; 3). Viết phương trình đường thẳng $\Delta$ đi qua trọng tâm G của tam giác ABC và vuông góc với mp(ABC).

Một học sinh làm như sau:

Bước 1: Tọa độ trong tâm G của tam giác ABC là

$\left\{ \matrix{ {x_G} = {{1 + 1 + 1} \over 3} = 1 \hfill \cr  {y_G} = {{3 + 2 + 1} \over 3} = 2 \hfill \cr  {z_G} = {{2 + 1 + 3} \over 3} = 2. \hfill \cr} \right.$

Bước 2: Vectơ pháp tuyến của mp(ABC) là $\overrightarrow n  = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( { - 3;1;0} \right).$

Bước 3:Phương trình tham số của đường thẳng $\Delta$ là:

$\left\{ \matrix{ x = 1 - 3t \hfill \cr  y = 2 + t \hfill \cr  z = 2. \hfill \cr} \right.$

Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?

(A) Đúng;                                    (B) Sai ở bước 1;

(C) Sai ở bước 2;                      (D) Sai ở bước 3.

Lời giải chi tiết:

$\overrightarrow {AB}  = \left( {0, - 1, - 1} \right),\overrightarrow {AC}  = \left( {0, - 2,1} \right),\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( { - 3,0,0} \right).$
Chọn (C).

Câu 28

Gọi d là đường thẳng đi qua gốc tọa độ O, vuông góc với trục Ox và vuông góc với đường thẳng

$\Delta :\left\{ \matrix{ x = 1 + t \hfill \cr  y = 2 - t \hfill \cr  z = 1 - 3t. \hfill \cr} \right.$

Phương trình của d là:
(A) 

$\left\{ \matrix{ x = t \hfill \cr  y = 3t \hfill \cr  z = - t\,; \hfill \cr} \right.$

(B) 

$\left\{ \matrix{ x = 1 \hfill \cr  y = - 3t \hfill \cr  z = - t\,; \hfill \cr} \right.$

(C) ${x \over 1} = {y \over 3} = {z \over { - 1}};$ 

(D)

$\left\{ \matrix{ x = 0 \hfill \cr  y = - 3t \hfill \cr  z = t\,. \hfill \cr} \right.$

Lời giải chi tiết:

Ox có vectơ chỉ phương $\overrightarrow i  = \left( {1,0,0} \right).$
$\Delta$ có vectơ chỉ phương $\overrightarrow u  = \left( {1, - 1, - 3} \right).$
d có vectơ chỉ phương $\overrightarrow a  = \left[ {\overrightarrow i ,\overrightarrow u } \right] = \left( {0,3, - 1} \right).$
Chọn (D).

Câu 29

Cho đường thẳng 

$d:\left\{ \matrix{ x = 3 + 4t \hfill \cr  y = - 1 - t \hfill \cr  z = 4 + 2t\, \hfill \cr} \right.$ và mặt phẳng $\left( P \right):x + 2y - z + 3 = 0.$ Trong các mệnh đề sau đây, mệnh đề nào đúng?

(A) d song song với (P);                  (B) d cắt (P);

(C) d vuông góc với (P);                   (D) d nằm trên (P).

Lời giải chi tiết:

$A\left( {3, - 1,4} \right),B\left( { - 1,0,2} \right) \in d$ và $A,B \in \left( P \right).$
Chọn (D).

Câu 30

Cho điểm A(1; 1; 1) và đường thẳng

$d:\left\{ \matrix{ x = 6 - 4t \hfill \cr  y = - 2 - t \hfill \cr  z = - 1 + 2t\,. \hfill \cr} \right.$

Hình chiếu của A trên d có tọa độ là

(A) $\left( {2; - 3;1} \right);$                    (B) $\left( {2; - 3; - 1} \right);$

(C) $(2; 3; 1)$;                          (D) $\left( { - 2;3;1} \right).$

Lời giải chi tiết:

Giả sử $H\left( {6 - 4t, - 2 - t, - 1 + 2t} \right)$ là hình chiếu của A trên d. Ta có $\overrightarrow {AH}$vuông góc với $\overrightarrow u  = \left( { - 4, - 1,2} \right)$ (là vectơ chỉ phương của d).

Ta có $\overrightarrow {AH}  = \left( {5 - 4t, - 3 - t, - 2 + 2t} \right).$
$\overrightarrow {AH} .\overrightarrow u  = 0 \Leftrightarrow  - 4\left( {5 - 4t} \right) + 3 + t + 2\left( { - 2 + 2t} \right) = 0 \Leftrightarrow t = 1.$
Vậy $H\left( {2, - 3,1} \right).$
Chọn (A).

Câu 31

Cho tứ diện ABCD có A(1; 0; 0), B(1; 1; 0), C(0; 1; 0) và D(0; 0; 2).

Tính khoảng cách giữa hai đường thẳng AC và BD.

Một học sinh làm như sau:

Bước 1: $\overrightarrow {AC}  = \left( { - 1;1;0} \right),\,\,\overrightarrow {BD}  = \left( { - 1; - 1;2} \right),\,\,\overrightarrow {AB}  = \left( {0;1;0} \right).$

Bước 2: $\left[ {\overrightarrow {AC} ,\overrightarrow {BD} } \right] = \left( {2;2;2} \right)$.

Bước 3: $d\left( {AC,BD} \right) = {{\left| {\left[ {\overrightarrow {AC} ,\overrightarrow {BD} } \right].\overrightarrow {AB} } \right|} \over {\left| {\left[ {\overrightarrow {AC} ,\overrightarrow {BD} } \right]} \right|}} = {2 \over {\sqrt {12} }} = {{\sqrt 3 } \over 3}.$

Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?

(A) Đúng;                     (B) Sai ở bước 1;

(C) Sai ở bước 2;         (D) Sai ở bước 3.

Lời giải chi tiết:

Bài toán trên đúng.
Chọn (A).

Câu 32

Cho $\left| {\overrightarrow u } \right| = 2,\left| {\overrightarrow v } \right| = 1,\left( {\overrightarrow u ,\overrightarrow v } \right) = {\pi  \over 3}.$ Góc giữa vectơ $\overrightarrow u$ và $\overrightarrow u  - \overrightarrow v$ bằng:

(A) ${30^0}$                 (B) ${45^0}$           

(C) ${60^0}$                 (D) ${90^0}$

Lời giải chi tiết:

Ta có

$\eqalign{ & \overrightarrow u .\overrightarrow v = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = 2.1.{1 \over 2} = 1 \cr  & \Rightarrow \overrightarrow v \left( {\overrightarrow u - \overrightarrow v } \right) = \overrightarrow u .\overrightarrow v - {\left| {\overrightarrow v } \right|^2} = 1 - 1 = 0 \cr  & \Rightarrow \overrightarrow v \bot \left( {\overrightarrow u - \overrightarrow v } \right). \cr}$

Chọn (D).

Câu 33

Cho $\left| {\overrightarrow u } \right| = 2,\left| {\overrightarrow v } \right| = 5,\left( {\overrightarrow u ,\overrightarrow v } \right) = {\pi  \over 6}.$ Độ dài vectơ $\left[ {\overrightarrow u ,\overrightarrow v } \right]$ bằng:

(A) 10                      (B) 5;             

(C) 8;                  (D) $5\sqrt 3$

Lời giải chi tiết:

$\left| {\left[ {\overrightarrow u ,\overrightarrow v } \right]} \right| = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.\sin \left( {\overrightarrow u ,\overrightarrow v } \right) = 2.5.{1 \over 2} = 5.$
Chọn (B).

Câu 34

Mặt phẳng $2x - 3y + z - 1 = 0$ cắt các trục tọa độ tại các điểm:

(A) $\left( {{1 \over 2};0;0} \right)\,\,,\,\,\left( {0; - {1 \over 3};0} \right)\,\,,\,\,\left( {0;0;1} \right);$
(B) $\left( {1;0;0} \right)\,\,,\,\,\left( {0;{1 \over 3};0} \right)\,\,,\,\,\left( {0;0;1} \right);$
(C) $\left( {{1 \over 2};0;0} \right)\,\,,\,\,\left( {0;{1 \over 3};0} \right)\,\,,\,\,\left( {0;0;1} \right);$
(D) $\left( {{1 \over 2};0;0} \right)\,\,,\,\,\left( {0; - {1 \over 3};0} \right)\,\,,\,\,\left( {0;0; - 1} \right).$

Lời giải chi tiết:

$\eqalign{ & y = z = 0 \Rightarrow x = {1 \over 2},x = z = 0 \Rightarrow y = - {1 \over 3}. \cr  & x = y = 0 \Rightarrow z = 1. \cr}$

Chọn (A).

Câu 35

Cho đường thẳng 

$d:\left\{ \matrix{ x = - {9 \over 5} - t \hfill \cr  y = 5t \hfill \cr  z = {7 \over 5} + 3t\, \hfill \cr} \right.$ và mặt phẳng $\left( P \right):3x - 2y + 3z - 1 = 0.$ Gọi d’ là hình chiếu của d trên (P). Trong các vectơ sau, vectơ nào không phải là vectơ chỉ phương của d’ ?

(A) $\left( {5; - 51;39} \right);$

(B) $\left( {10; - 102; - 78} \right);$

(C) $\left( { - 5;51;39} \right);$

(D) $\left( {5;51;39} \right).$

Lời giải chi tiết:

Vì ba vectơ của (A), (B), (C) cùng phương nên chọn (D).

Câu 36

Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Gọi M, N, P lần lượt là trung điểm của A’B’, BC, DD’. Chứng minh rằng $AC' \bot \left( {MNP} \right).$

Một học sinh làm như sau:

Bước 1: Chọn hệ trục tọa độ như hình 71;

Khi đó A(0; 0; 0), C’(1; 1; 1),

$M = \left( {{1 \over 2};0;1} \right),N\left( {1;{1 \over 2};0} \right),P\left( {0;1;{1 \over 2}} \right).$
Bước 2: $\overrightarrow {AC'}  = \left( {1;1;1} \right),\overrightarrow {MN}  = \left( {{1 \over 2};{1 \over 2}; - 1} \right),\overrightarrow {MP}  = \left( { - {1 \over 2};1; - {1 \over 2}} \right).$

Bước 3: 

$\left\{ \matrix{ \overrightarrow {AC'} .\overrightarrow {MN} = 0 \hfill \cr  \overrightarrow {AC'} .\overrightarrow {MP} = 0 \hfill \cr} \right. \Rightarrow AC' \bot \left( {MNP} \right).$

Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?

(A) Đúng;                             (B) Sai ở bước 1;

(C) Sai ở bước 2;                           (D) Sai ở bước 3.

Lời giải chi tiết:

Bài toán trên giải đúng

chọn A

Câu 37

Cho đường thẳng

$d:\left\{ \matrix{ x = 0 \hfill \cr  y = t \hfill \cr  z = 2 - t. \hfill \cr} \right.$

Phương trình đường vuông góc chung của d và trục Ox là:
(A) 

$\left\{ \matrix{ x = 1 \hfill \cr  y = t \hfill \cr  z = t\,; \hfill \cr} \right.$

(B) 

$\left\{ \matrix{ x = 0 \hfill \cr  y = 2t \hfill \cr  z = t\,; \hfill \cr} \right.$

(C)

$\left\{ \matrix{ x = 0 \hfill \cr  y = 2 - t \hfill \cr  z = t\,; \hfill \cr} \right.$

(D) 

$\left\{ \matrix{ x = 0 \hfill \cr  y = t \hfill \cr  z = t\,. \hfill \cr} \right.$

Lời giải chi tiết:

Phương trình tham số của trục Ox là

$\left\{ \matrix{ x = t \hfill \cr  y = 0 \hfill \cr  z = 0 \hfill \cr} \right.$

Lấy $P\left( {0,t,2 - t} \right) \in d$ và $Q'\left( {t',0,0} \right) \in {\rm{Ox}}{\rm{.}}$
$\overrightarrow {PQ}  = \left( {t', - t,t - 2} \right),$ d có vectơ chỉ phương $\overrightarrow u  = \left( {0,1, - 1} \right).$
PQ là đường vuông góc chung của d và trục Ox

$\Leftrightarrow \left\{ \matrix{ \overrightarrow {PQ} .\overrightarrow u = 0 \hfill \cr  \overrightarrow {PQ} .\overrightarrow i = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ - t - t + 2 = 0 \hfill \cr  t' = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ t = 1 \hfill \cr  t' = 0 \hfill \cr} \right..$

Vậy $P\left( {0,1,1} \right),Q\left( {0,0,0} \right).$
PQ có phương trình

$\left\{ \matrix{ x = 0 \hfill \cr  y = t \hfill \cr  z = t \hfill \cr} \right..$

Chọn (D).

Câu 38

Cho mặt phẳng (P): $x - 2y - 3z + 14 = 0$ và điểm $M\left( {1; - 1;1} \right)$. Tọa độ của điểm M’ đối xứng với M qua mp(P) là

(A) $\left( { - 1;3;7} \right);$                   

(B) $\left( {1; - 3;7} \right);$

(C) $\left( {2; - 3; - 2} \right);$ 

(D) $\left( {2; - 1;1} \right).$

Lời giải chi tiết:

(P) có vectơ pháp tuyến $\overrightarrow n  = \left( {1, - 2, - 3} \right).$
$M'\left( {x,y,z} \right)$ đối xứng với M qua mp(P) khi và chỉ khi  $\overrightarrow {MM'}$ cùng phương với $\overrightarrow n$ và trung điểm I của MM’ nằm trên (P).
Ta có hệ:

$\left\{ \matrix{ {{x - 1} \over 1} = {{y + 1} \over { - 2}} = {{z - 1} \over { - 3}} \hfill \cr  {{x + 1} \over 2} - 2{{y - 1} \over 2} - 3{{z + 1} \over 2} + 14 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - 1 \hfill \cr  y = 3 \hfill \cr  z = 7 \hfill \cr} \right..$

Chọn (A).

Câu 39

Cho điểm $A\left( {0; - 1;3} \right)$ và đường thẳng

$d:\left\{ \matrix{ x = 1 + 2t \hfill \cr  y = 2 \hfill \cr  z = - t\,. \hfill \cr} \right.$

Khoảng cách từ A đến d bằng:

(A) $\sqrt 3 ;$             (B) $\sqrt {14} ;$                 

(C) $\sqrt 6 ;$              (D) $\sqrt 8 .$

Lời giải chi tiết:

d đi qua $M(1, 2, 0)$ có vectơ chỉ phương $\overrightarrow u  = \left( {2,0, - 1} \right).$
Khoảng cách từ A đến d bằng ${{\left| {\left[ {\overrightarrow {AM} ,\overrightarrow u } \right]} \right|} \over {\left| {\overrightarrow u } \right|}} = \sqrt {14} .$
Chọn (B).

Câu 40

Cho điểm $M\left( { - 1;2; - 3} \right).$ Gọi ${M_1},{M_2},{M_3}$ lần lượt là điểm đối xứng của M qua các mặt phẳng (Oxy), (Oxz), (Oyz). Phương trình $mp\left( {{M_1}{M_2}{M_3}} \right)$ là:

(A) $6x + 2y + 3z + 6 = 0;$ 

(B) $6x - 2y + 3z + 6 = 0;$

(C) $6x - 3y + 2z + 6 = 0;$

(D) $6x - 3y - 2z + 6 = 0.$

Lời giải chi tiết:

${M_1}\left( { - 1,2,3} \right),{M_2}\left( { - 1, - 2, - 3} \right),{M_3}\left( {1,2, - 3} \right);mp\left( {{M_1}{M_2}{M_3}} \right)$ qua có vectơ pháp tuyến $\overrightarrow n  = \left[ {\overrightarrow {{M_1}{M_2}} ,\overrightarrow {{M_1}{M_3}} } \right].$
Chọn (C).

Câu 41

Cho mặt cầu $\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z - 2} \right)^2} = 49.$ Phương trình nào sau đây là phương trình của mặt phẳng tiếp xúc với mặt cầu (S) ?

(A) $6x + 2y + 3z = 0;$

(B) $2x + 3y + 6z - 5 = 0;$

(C) $6x + 2y + 3z - 55 = 0;$ 

(D) $x + 2y + 2z - 7 = 0.$

Lời giải chi tiết:

(S) có tâm $I\left( {1, - 3,2} \right),$ bán kính R = 7.
$d\left( {I,\left( P \right)} \right) = 7.$
Chọn (C).

Câu 42

Cho mặt cầu (S): ${x^2} + {y^2} + {z^2} - 2x - 4y - 6z = 0.$ Trong ba điểm (0; 0; 0); (1; 2; 3), (2; -1; -1), có bao nhiêu điểm nằm trong mặt cầu (S) ?

(A) 0 ;                         (B) 1 ;                   

(C) 2 ;                         (D) 3.

Lời giải chi tiết:

Lần lượt thay tọa độ ba điểm đã cho vào (S). Ta có $O \in \left( S \right).$

Chọn (B).

Loigiaihay.com