Phương pháp giải:

- Dựng tâm mặt cầu ngoại tiếp tứ diện.

- Xác định góc giữa $OO'$ và mặt phẳng $\left( {ABC} \right)$, chú ý tìm một đường thẳng song song với $OO'$ suy ra góc.

Lời giải chi tiết:

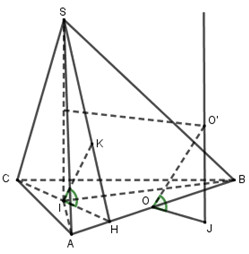
Gọi $J$  tâm đường tròn ngoại tiếp tam giác $IAB$.

Qua $J$ kẻ đường thẳng vuông góc với $\left( {IAB} \right)$, cắt mặt phẳng trung trực của $SI$ tại $O'$ thì $O'$ là tâm mặt cầu ngoại tiếp tứ diện $SIAB$.

Lại có $O'J \bot \left( {ABC} \right) \Rightarrow \widehat {\left( {OO',\left( {ABC} \right)} \right)} = \widehat {\left( {OO',OJ} \right)}$.

Do tam giác $SAB$ vuông nên $OO'$ là trục đường tròn ngoại tiếp tam giác $SAB$ hay $OO' \bot \left( {SAB} \right)$.

Kẻ $IK \bot SH$. Ta có $\left\{ \begin{array}{l}AB \bot AH\\AB \bot SI\end{array} \right. \Rightarrow AB \bot \left( {SIH} \right) \Rightarrow AB \bot IK$.

Do đó $IK \bot \left( {SAB} \right)$ nên $IK//OO'$.

Ngoài ra $OJ \bot AB$ (trung trực của $AB$) và $IH \bot AB$ nên $IH//OJ$.

Từ đó $\widehat {\left( {OO',OJ} \right)} = \widehat {\left( {IK,IH} \right)} = \widehat {KIH}$.

Trong các tam giác vuông $CAB,SAB$ ta có: $C{H^2} = HA.HB = S{H^2} \Rightarrow CH = SH$.

Lại có $SI$ vừa là đường cao vưà là trung tuyến trong tam giác $SCH$ nên tam giác $SCH$ cân tại $S \Rightarrow SC = SH = CH$ hay tam giác $SCH$ đều.

$\Rightarrow \widehat {KHI} = {60^0} \Rightarrow \widehat {KIH} = {30^0}$.

Vậy góc giữa $OO'$ và $\left( {ABC} \right)$ bằng ${30^0}$.

Chọn B.