Phương pháp giải:

+) Gọi $M$ là trung điểm của $CD$, $O = AC \cap BD,\,\,H = AM \cap OD$. Chứng minh $\angle \left( {BG;SA} \right) = \angle \left( {BG;HG} \right)$.

+) Áp dụng định lí Cosin trong tam giác.

Lời giải chi tiết:

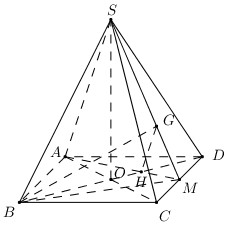
Gọi $M$ là trung điểm của $CD$, $O = AC \cap BD,\,\,H = AM \cap OD$.
Xét tam giác $ACD$ có $H$ là trọng tâm tam giác $\Rightarrow \dfrac{{MH}}{{MA}} = \dfrac{1}{3}$.
Ta có: $\dfrac{{MH}}{{MA}} = \dfrac{{MG}}{{MS}} = \dfrac{1}{3} \Rightarrow HG//SA$ (Định lí Ta-lét đảo)
$\Rightarrow \alpha = \angle \left( {BG;SA} \right) = \angle \left( {BG;HG} \right)$.
Ta có $HG = \dfrac{1}{3}SA = \dfrac{{a\sqrt 3 }}{3}$.
$H$ là trọng tâm tam giác $ACD$ $\Rightarrow OH = \dfrac{1}{3}OD = \dfrac{1}{3}.\dfrac{1}{2}.BD = \dfrac{1}{6}BD$
$\Rightarrow BH = \dfrac{1}{2}BD + \dfrac{1}{6}BD = \dfrac{2}{3}BD = \dfrac{2}{3}.a\sqrt 2$.
Ta có $BM = \sqrt {{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 5 }}{2},\,\,SM = \sqrt {3{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt {11} }}{2}$.
Áp dụng định lí Cosin trong tam giác $SBM$ ta có:
$\cos \angle SMB = \dfrac{{S{M^2} + B{M^2} - S{B^2}}}{{2SM.BM}} = \dfrac{{\dfrac{{11{a^2}}}{4} + \dfrac{{5{a^2}}}{4} - 3{a^2}}}{{2\dfrac{{a\sqrt {11} }}{2}.\dfrac{{a\sqrt 5 }}{2}}} = \dfrac{{2\sqrt {55} }}{{55}}$
Ta có $GM = \dfrac{1}{3}SM = \dfrac{{a\sqrt {11} }}{6}$.
Áp dụng định Cosin trong tam giác $BMG$ ta có:
$\begin{array}{l}B{G^2} = M{B^2} + M{G^2} - 2MB.MG.\cos \angle SMB\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{5{a^2}}}{4} + \dfrac{{11{a^2}}}{{36}} - 2.\dfrac{{a\sqrt 5 }}{2}.\dfrac{{a\sqrt {11} }}{6}.\dfrac{{2\sqrt {55} }}{{55}}\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{11}}{9}{a^2} \Rightarrow BG = \dfrac{{\sqrt {11} a}}{3}\end{array}$
Áp dụng định lí Cosin trong tam giác $BHG$ ta có:
$\cos \angle BGH = \dfrac{{G{B^2} + G{H^2} - B{H^2}}}{{2.GB.GH}} = \dfrac{{\dfrac{{11{a^2}}}{9} + \dfrac{{{a^2}}}{3} - \dfrac{{8{a^2}}}{9}}}{{2.\dfrac{{a\sqrt {11} }}{3}.\dfrac{{a\sqrt 3 }}{3}}} = \dfrac{2}{3}.\dfrac{{3\sqrt {33} }}{{22}} = \dfrac{{\sqrt {33} }}{{11}} > 0$.
Vậy $\cos \alpha = \dfrac{{\sqrt {33} }}{{11}}$.

Chọn A.