Phương pháp giải:

+) Dựng trục của 2 mặt phẳng $\left( {ABCD} \right)$ và $\left( {SAB} \right)$, xác định giao điểm, chứng minh giao điểm đó là tâm mặt cầu ngoại tiếp chóp $S.ABCD$.

+) Sử dụng định lí Pytago và các kiến thức cơ bản tính bán kính $R$ mặt cầu ngoại tiếp chóp $S.ABCD$, sử dụng công thức tính diện tích mặt cầu $S = 4\pi {R^2}$.

Lời giải chi tiết:

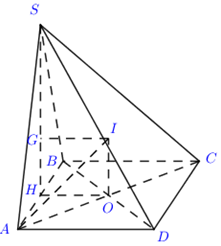
Gọi H là trung điểm của AB ta có $SH \bot AB \Rightarrow SH \bot \left( {ABCD} \right)$.

Gọi $O = AC \cap BD$, $G$ là trọng tâm tam giác đều $SAB$.

Qua $O$ dựng ${d_1}//SH \Rightarrow {d_1} \bot \left( {ABCD} \right)$, qua $G$ dựng ${d_2}//OH \Rightarrow {d_2} \bot \left( {SAB} \right)$.

Gọi $I = {d_1} \cap {d_2}$ ta có :

$\left\{ \begin{array}{l}I \in {d_1} \Rightarrow IA = IB = IC = ID\\I \in {d_2} \Rightarrow IA = IB = IS\end{array} \right. \Rightarrow IA = IB = IC = ID = IS$

$\Rightarrow I$ là tâm mặt cầu ngoại tiếp chóp $S.ABCD$.  

Tam giác $SAB$ đều cạnh $a \Rightarrow SH = \frac{{a\sqrt 3 }}{2} \Rightarrow HG = \frac{1}{3}SH = \frac{{a\sqrt 3 }}{6} = OI$.

Ta có $AC = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{a^2} + 4{a^2}}  = a\sqrt 5  \Rightarrow OA = \frac{{a\sqrt 5 }}{2}$.

Áp dụng định Pytago trong tam giác vuông $OAI$ ta có: $IA = \sqrt {I{O^2} + O{A^2}}  = \sqrt {\frac{{{a^2}}}{{12}} + \frac{{5{a^2}}}{4}}  = \frac{{2\sqrt 3 a}}{3} = R$

Vậy $S = 4\pi {R^2} = 4\pi \frac{{4{a^2}}}{3} = \frac{{16\pi {a^2}}}{3}$.

Chọn B.