Phương pháp giải:

$\left\{ \begin{array}{l}\left( \alpha  \right) \bot \left( \gamma  \right)\\\left( \beta  \right) \bot \left( \gamma  \right)\\\left( \alpha  \right) \cap \left( \beta  \right) = d\end{array} \right. \Rightarrow d \bot \left( \gamma  \right)$

Lời giải chi tiết:

Ta có: $\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABC} \right)\\\left( {SAC} \right) \bot \left( {ABC} \right)\\\left( {SAB} \right) \cap \left( {SAC} \right) = SA\end{array} \right. \Rightarrow SA \bot \left( {ABC} \right)$

Gọi I, F lần lượt là trung điểm của SC, SA, AC

Do tam giác ABC vuông tại B

$\Rightarrow$ F là tâm đường tròn ngoại tiếp tam giác ABC (1)

IF là đường trung bình của tam giác SAC $\Rightarrow$IF // SA

Mà $SA \bot \left( {ABC} \right) \Rightarrow IF \bot \left( {ABC} \right)$ (2)

Từ (1), (2) suy ra $IA = IB = IC$

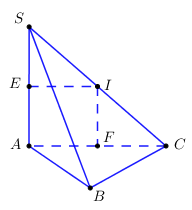
Lại có: tam giác SAC vuông tại A $\Rightarrow I$ là tâm đường tròn ngoại tiếp tam giác SAC

$\Rightarrow \,IS = IA = IC$$\Rightarrow \,IS = IA = IB = IC \Rightarrow I$ là tâm mặt cầu ngoại tiếp hình chóp S.ABC.

Chọn: C