Phương pháp giải:

Thể tích khối nón $V = \dfrac{1}{3}\pi {r^2}h$.

Lời giải chi tiết:

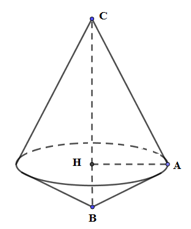
Dựng $AH \bot BC,\left( {H \in BC} \right)$. Khi quay tam giác $ABC$ quanh cạnh $BC$ta được 2 khối nón có chung đáy là hình tròn tâm H bán kính AH và chiều cao tương ứng là CH, BH.

Tam giác ABC vuông tại A, $\widehat {ACB} = 30^\circ  \Rightarrow BC = \dfrac{{AB}}{{\sin 30^\circ }} = 2a,\,\,AC = AB.\cot 30^\circ  = a\sqrt 3$

Ta có: $AH \bot BC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{a.\sqrt 3 a}}{{2a}} = \dfrac{{\sqrt 3 }}{2}a$

Thể tích khối tròn xoay tạo thành là: 

$V = \dfrac{1}{3}\pi .A{H^2}.CH + \dfrac{1}{3}\pi .A{H^2}.BH = \dfrac{1}{3}\pi .A{H^2}.BC = \dfrac{1}{3}\pi .{\left( {\dfrac{{\sqrt 3 }}{2}a} \right)^2}.2a = \dfrac{{\pi {a^3}}}{2}$

Chọn: D