Phương pháp giải:

+) Sử dụng công thức: \(h = \sqrt {{l^2} - {R^2}} .\)

+) Thể tích hình nón có bán kính R và đường cao h  là: \(V = \dfrac{1}{3}\pi {R^2}h.\)

Lời giải chi tiết:

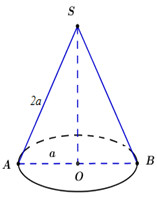
Xét \(\Delta SAO\) vuông tại \(O\)  có: \(SO = \sqrt {S{A^2} - A{O^2}}  = \sqrt {{{\left( {2a} \right)}^2} - {a^2}}  = a\sqrt 3 .\)

Khi đó ta có: \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi .{a^2}.a\sqrt 3  = \dfrac{{\pi {a^3}\sqrt 3 }}{3}.\)

CHỌN A