Câu hỏi:
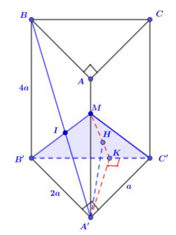
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại A. Biết \(AB = 2a\),\(AC = a,\,\,AA' = 4a\). Gọi M là điểm thuộc cạnh AA’ sao cho \(MA' = 3MA\). Tính khoảng cách giữa hai đường thẳng chéo nhau \(BC\) và \(C'M\).
- A \(\dfrac{{6a}}{7}\).
- B \(\dfrac{{8a}}{7}\).
- C \(\dfrac{{4a}}{3}\).
- D \(\dfrac{{4a}}{7}\).
Phương pháp giải:
Lời giải chi tiết:
Gọi \(I = B'M \cap BA'\), ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}BC//B'C'\\BC \not\subset \left( {MB'C'} \right)\end{array} \right. \Rightarrow BC//\left( {MB'C'} \right)\\ \Rightarrow d\left( {BC;C'M} \right) = d\left( {BC;\left( {MB'C'} \right)} \right) = d\left( {B;\left( {MB'C'} \right)} \right)\end{array}\)
Mà hai tam giác IMA’ và IB’B đồng dạng, nên:
\(\dfrac{{IA'}}{{IB}} = \dfrac{{MA'}}{{BB'}} = \dfrac{3}{4} \Rightarrow IA' = \dfrac{3}{4}IB \Rightarrow d\left( {B;\left( {MB'C'} \right)} \right) = \dfrac{4}{3}d\left( {A';\left( {MB'C'} \right)} \right)\)
Dựng \(A'K \bot B'C'\)tại K, \(A'H \bot MK\) tại H, ta có:
\(\left\{ \begin{array}{l}B'C' \bot A'K\\B'C' \bot MA'\end{array} \right. \Rightarrow B'C' \bot \left( {MA'K} \right) \Rightarrow A'H \bot B'C'\)
Mà \(A'H \bot MK \Rightarrow A'H \bot \left( {MB'C'} \right) \Rightarrow d\left( {A';\left( {MB'C'} \right)} \right) = A'H\)
Xét tam giác A’B’C’ vuông tại A’ có: \(\dfrac{1}{{A'{K^2}}} = \dfrac{1}{{A'B{'^2}}} + \dfrac{1}{{A'C{'^2}}} = \dfrac{1}{{4{a^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{5}{{4{a^2}}}\)
Xét tam giác MA’K vuông tại A’ có: \(\dfrac{1}{{A'{H^2}}} = \dfrac{1}{{A'{K^2}}} + \dfrac{1}{{A'{M^2}}} = \dfrac{5}{{4{a^2}}} + \dfrac{1}{{9{a^2}}} = \dfrac{{49}}{{36{a^2}}} \Rightarrow A'H = \dfrac{{6a}}{7}\)
Vậy \(d\left( {BC;C'M} \right) = \dfrac{4}{3}A'H = \dfrac{4}{3}.\dfrac{{6a}}{7} = \dfrac{{8a}}{7}\).
Chọn: B