Câu hỏi:
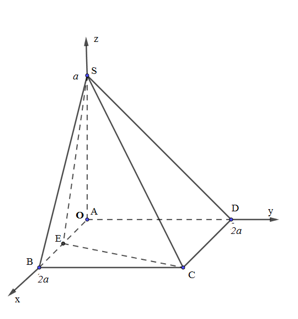
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, \(SA \bot \left( {ABCD} \right)\) và \(SA = a\). Gọi E là trung điểm của cạnh AB. Diện tích mặt cầu ngoại tiếp hình chóp \(S.BCE\) bằng
- A \(14\pi {a^2}\).
- B \(11\pi {a^2}\).
- C \(8\pi {a^2}\).
- D \(12\pi {a^2}\).
Phương pháp giải:
Sử dụng phương pháp tọa độ hóa.
Lời giải chi tiết:
Gắn hệ trục tọa độ như hình vẽ.
Trong đó, \(B\left( {2a;0;0} \right),\,\,C\left( {2a;2a;0} \right),\,\,E\left( {a;0;0} \right),\,S\left( {0;0;a} \right)\)
Gọi \(I\left( {{x_0};{y_0};{z_0}} \right)\) là tâm của mặt cầu ngoại tiếp hình chóp S.BEC. Khi đó, \(I{S^2} = I{B^2} = I{C^2} = I{E^2}\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_0}^2 + {y_0}^2 + {\left( {{z_0} - a} \right)^2} = {\left( {{x_0} - 2a} \right)^2} + {y_0}^2 + {z_0}^2\\{x_0}^2 + {y_0}^2 + {\left( {{z_0} - a} \right)^2} = {\left( {{x_0} - 2a} \right)^2} + {\left( {{y_0} - 2a} \right)^2} + {z_0}^2\\{x_0}^2 + {y_0}^2 + {\left( {{z_0} - a} \right)^2} = {\left( {{x_0} - a} \right)^2} + {y_0}^2 + {z_0}^2\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l} - 2a{z_0} + {a^2} = - 4a{x_0} + 4{a^2}\\ - 2a{z_0} + {a^2} = \, - 4a{x_0} + 4{a^2} - 4a{y_0} + 4{a^2}\\ - 2a{z_0} + {a^2} = - 2a{x_0} + {a^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4{x_0} - 2{z_0} = 3a\\4{x_0} + 4{y_0} - 2{z_0} = 7a\\{x_0} - {z_0} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = \frac{{3a}}{2}\\{y_0} = a\\{z_0} = \frac{{3a}}{2}\end{array} \right.\)
Bán kính mặt cầu: \(R = SI = \sqrt {{x_0}^2 + {y_0}^2 + {{\left( {{z_0} - a} \right)}^2}} = \sqrt {\frac{{9{a^2}}}{4} + {a^2} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt {14} }}{2}\)
Diện tích mặt cầu : \(S = 4\pi {R^2} = 14\pi {a^2}\).
Chọn: A