Câu hỏi:
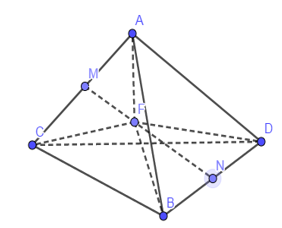
Cho tứ diện ABCD thỏa mãn \(AB=CD=\sqrt{34}\) , \(BC=AD=\sqrt{41}\) , \(AC=BD=5\) Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD
- A \(r=5\sqrt{2}\)
- B \(r=\frac{5\sqrt{2}}{2}\)
- C \(r=\frac{1}{\sqrt{10}}\)
- D \(r=\sqrt{10}\)
Phương pháp giải:
Cho chóp tam giác có các cặp cạnh đối lần lượt bằng nhau , đoạn thẳng nối trung điểm của 2 cặp cạnh đối đó sẽ vuông góc với 2 cạnh đó
Lời giải chi tiết:
Ta có \(M{{B}^{2}}=\frac{A{{B}^{2}}+B{{C}^{2}}}{2}-\frac{A{{C}^{2}}}{4}=\frac{125}{4}\)
Tương tự ta có \(M{{D}^{2}}=\frac{125}{4}\)
Suy ra : \(M{{N}^{2}}=\frac{M{{D}^{2}}+M{{B}^{2}}}{2}-\frac{B{{D}^{2}}}{4}=25\)
Gọi F là tâm đường tròn ngoại tiếp chóp . Vì MN là trung trực của BD và AC nên sẽ tồn tại một điểm trên MN cách đều cả 4 điểm A;B;C;D. Ta có hệ
\(\left\{ \begin{align} & FM+FN=5 \\ & F{{M}^{2}}+{{\left( \frac{AC}{2} \right)}^{2}}=F{{N}^{2}}+{{\left( \frac{BD}{2} \right)}^{2}}=R \\\end{align} \right.=>FM=FN=\frac{5}{2}=>R=\frac{5\sqrt{2}}{2}\)
Chọn đáp án B