Phương pháp giải:

Gọi thể tích tứ diện ABCD là V, tính thể tích các phần theo V dựa vào tỉ số đường cao, tỉ số diện tích đáy tương ứng.

Lời giải chi tiết:

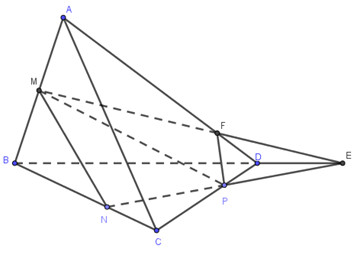
Gọi E là giao điểm của NP và BD, F là giao điểm của ME và AD.

Khi đó, thiết diện của (MNP) và tứ diện ABCD là tứ giác MNPF.

Áp dụng định lí Menelaus trong tam giác BCD ta có $\frac{{NB}}{{NC}}.\frac{{PC}}{{PD}}.\frac{{EB}}{{ED}} = 1 \Leftrightarrow 2.2.\frac{{EB}}{{ED}} = 1 \Rightarrow \frac{{EB}}{{ED}} = \frac{1}{4}$

$\Rightarrow BE = \frac{4}{3}BD$

Áp dụng định lí Menelaus trong tam giác ABD có: $\frac{{MA}}{{MB}}.\frac{{EB}}{{ED}}.\frac{{FD}}{{FA}} = 1 \Leftrightarrow \frac{{FD}}{{FA}} = \frac{1}{4} \Rightarrow \frac{{FD}}{{AD}} = \frac{1}{5}$

$\begin{array}{l} \Rightarrow \frac{{{S_{BNE}}}}{{{S_{BCD}}}} = \frac{{NB}}{{CB}}.\frac{{BE}}{{BD}} = \frac{2}{3}.\frac{4}{3} = \frac{8}{9}\\ \Rightarrow \frac{{{V_{M.BNE}}}}{{{V_{ABCD}}}} = \frac{{MB}}{{AB}}.\frac{{{S_{BNE}}}}{{{S_{BCD}}}} = \frac{1}{2}.\frac{8}{9} = \frac{4}{9} \Rightarrow {V_{M.BNE}} = \frac{4}{9}{V_{ABCD}}\end{array}$

$\begin{array}{l}\frac{{{S_{PDE}}}}{{{S_{BCD}}}} = \frac{{PD}}{{CD}}.\frac{{DE}}{{BD}} = \frac{1}{3}.\frac{1}{3} = \frac{1}{9}\\ \Rightarrow \frac{{{V_{F.PDE}}}}{{{V_{ABCD}}}} = \frac{{FD}}{{AD}}.\frac{{{S_{PDE}}}}{{{S_{BCD}}}} = \frac{1}{5}.\frac{1}{9} = \frac{1}{{45}} \Rightarrow {V_{F.PDE}} = \frac{1}{{45}}{V_{ABCD}}\\ \Rightarrow {V_{MNPFBD}} = {V_{M.BNE}} - {V_{F.PDE}} = \frac{{19}}{{45}}{V_{ABCD}} = {V_1}\\ \Rightarrow {V_2} = \frac{{26}}{{45}}{V_{ABCD}}\\ \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{{19}}{{26}}\end{array}$

Chọn: B.