Câu hỏi:
Một con lắc lò xo treo thẳng đứng với biên độ 8cm. Khoảng thời gian từ lúc lực đàn hồi cực đại đến lúc lực đàn hồi cực tiểu là T/3, với T là chu kì dao động của con lắc. Tốc độ của vật nặng khi nó cách vị trí thấp nhất 2cm. Lấy g =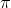 2 m/s2.
2 m/s2.
- A 83,12cm/s
- B 106,45cm/s
- C 87,66cm/s
- D 57,37cm/s
Phương pháp giải:
Sử dụng đường tròn lượng giác và hệ thức độc lập với thời gian của vận tốc và li độ
Lời giải chi tiết:
A = 8cm. Gọi ∆l là độ dãn của lò xo khi vật ở VTCB.
Xét 2 trường hợp:
+ Nếu \(A \le \Delta \ell \) thì vị trí lực đàn hồi cực tiểu ứng với vật ở biên trên, vậy thời gian từ lúc lực đàn hồi cực đại đến khi lực đàn hồi cực tiểu là T/2 => Không phù hợp với bài toán.
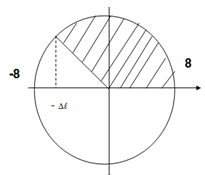
+ Khi \(\Delta \ell \le A\), vật đi từ vị trí lực đàn hồi cực đại ứng với vật ở biên dưới +A đến khi lực đàn hồi cực tiểu ứng với vị trí x = -\(\Delta \ell \), (biểu diễn như hình vẽ) hết thời gian T/3, ứng với góc 1200
Dựa vào hình vẽ ta được \(\Delta \ell = \frac{A}{2} = 4cm = 0,04m \Rightarrow \omega = \sqrt {\frac{g}{{\Delta \ell }}} = 5\pi \left( {rad/s} \right)\)
Khi vật cách vị trí thấp nhất 2cm ứng với x = 6cm, tốc độ của vật là:
\({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} \Leftrightarrow {8^2} = {6^2} + \frac{{{v^2}}}{{{5^2}{\pi ^2}}} \Rightarrow |v| = 83,119cm/s\)