Câu hỏi:
Một con lắc lò xo gồm lò xo có khối lượng không đáng kể, có độ cứng k = 100N/m, khối lượng của vật m = 1kg. Từ vị trí cân bằng kéo vật lệch khỏi vị trí cân bằng x = 3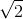 cm rồi thả nhẹ. Chọn gốc thời gian t = 0 là lúc vật qua vị trí x = - 3cm theo chiều dương. Phương trình dao động của vật là:
cm rồi thả nhẹ. Chọn gốc thời gian t = 0 là lúc vật qua vị trí x = - 3cm theo chiều dương. Phương trình dao động của vật là:
- A
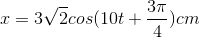
- B
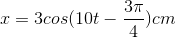
- C
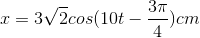
- D
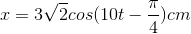
Phương pháp giải:
Lời giải chi tiết:
Đáp án C
Phương pháp : Xác đinh A, ω và φ của phương trình x = Acos(ωt + φ)
Tần số góc: \(\omega = \sqrt {{k \over m}} = 10{\rm{r}}a{\rm{d}}/s\)
Khi \({\rm{x}} = 3\sqrt 2 cm\) thì v = 0 nên \({\rm{A}} = \sqrt {{x^2} + {{{v^2}} \over {{\omega ^2}}}} = 3\sqrt 2 cm\)
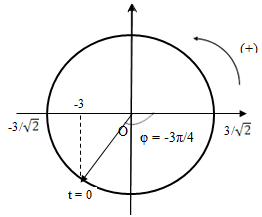
Chọn gốc thời gian t = 0 là lúc vật qua vị trí x = - 3cm theo chiều dương. Sử dụng vòng tròn lượng giác ta được pha ban đầu \(\varphi = - {{3\pi } \over 4}\) (rad)
Phương trình dao động điều hòa: \({\rm{x}} = 3\sqrt 2 c{\rm{os}}(10t - {{3\pi } \over 4})cm\)