Phương pháp giải:

Lời giải chi tiết:

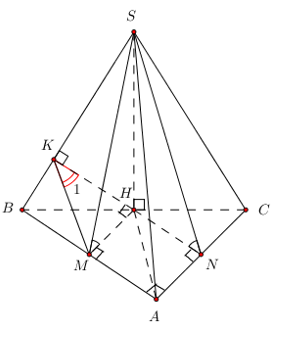
* Tính chất: Chóp có các cạnh bên bằng nhau thì chân đường vuông góc là tâm đường tròn ngoại tiếp đáy. Vẽ H là trung điểm BC $\Rightarrow SH \bot \left( {ABC} \right)$.

* Vẽ $HM \bot AB,\,\,HN \bot AC$ có $\widehat {\left( {\left( {SAB} \right);\left( {ABC} \right)} \right)} = \widehat M = {60^0}$, $\widehat {\left( {\left( {SAC} \right);\left( {ABC} \right)} \right)} = \widehat N = {60^0}$.

* ${\Delta _v}SHM = {\Delta _v}SHN \Rightarrow HM = HN$

$\Rightarrow {\Delta _v}HMB - {\Delta _v}HNC \Rightarrow \widehat B = \widehat C$

$\Rightarrow \Delta ABC$ vuông cân ở A.

* Tam giác vuông SHM: $SH = HM.\tan {60^0} = \frac{a}{2}\sqrt 3  = \frac{{a\sqrt 3 }}{2}$

* Dễ thấy $AH \bot \left( {SBC} \right)$. Vẽ $HK \bot SB \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {SBC} \right)} \right)} = \widehat {{K_1}}$

* $AH = \frac{{BC}}{2} = \frac{{a\sqrt 2 }}{2}$   

* Tam giác vuông SHB: $\frac{1}{{H{K^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{B{H^2}}} \Rightarrow HK = \frac{{a\sqrt 3 }}{{\sqrt {10} }}$

* Tam giác vuông AHK: $\tan \widehat {{K_1}} = \frac{{AH}}{{HK}} = \frac{{a\sqrt 2 }}{2}:\frac{{a\sqrt 3 }}{{\sqrt {10} }} = \sqrt {\frac{5}{3}}$

Chọn đáp án B.