Câu hỏi:
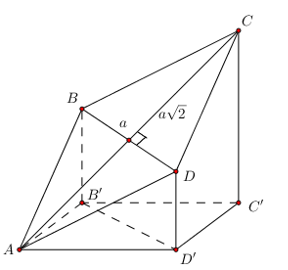
Cho hình thoi ABCD có \(A \in \left( P \right)\), các đỉnh khác không ở trong (P). BD = a, \(AC = a\sqrt 2 \). Chiếu vuông góc ABCD lên (P) ta được hình vuông AB’C’D’. Tính góc \(\widehat {\left( {\left( {ABCD} \right);\left( {AB'C'D'} \right)} \right)}\) . Biết \(BD//\left( P \right)\).
- A \({30^0}\)
- B \({45^0}\)
- C \({60^0}\)
- D \({90^0}\)
Phương pháp giải:
Lời giải chi tiết:
* BD // B’D’ \( \Rightarrow B'D' = BD = a\)
* \({S_{ABCD}} = \frac{1}{2}BD.AC = \frac{{{a^2}\sqrt 2 }}{2}\)
* \({S_{AB'C'D'}} = \frac{1}{2}B'D'.A'C' = \frac{1}{2}{\left( {B'D'} \right)^2} = \frac{{{a^2}}}{2}\)
* Áp dụng định lí diện tích hình chiếu ta có:
\(\begin{array}{l}{S_{AB'C'D'}} = {S_{ABCD}}.\cos \widehat {\left( {\left( {ABCD} \right);\left( {AB'C'D'} \right)} \right)}\\ \Rightarrow \cos \widehat {\left( {\left( {ABCD} \right);\left( {AB'C'D'} \right)} \right)} = \frac{{{S_{AB'C'D'}}}}{{{S_{ABCD}}}} = \frac{{{a^2}}}{2}:\frac{{{a^2}\sqrt 2 }}{2} = \frac{1}{{\sqrt 2 }}\\ \Rightarrow \widehat {\left( {\left( {ABCD} \right);\left( {AB'C'D'} \right)} \right)} = {45^0}\end{array}\).
Chọn đáp án B.